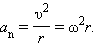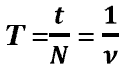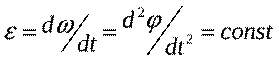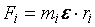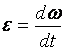Что называется массой системы материальных точек

СИСТЕМА МАТЕРИАЛЬНЫХ ТОЧЕК. ТВЁРДОЕ ТЕЛО

Системой материальных точек (или механической системой) называют такую совокупность точек, в которой положение или движение каждой точки зависит от положения и движения всех остальных.

Систему материальных точек, движение которых не ограничено никакими связями, а определяется лишь действующими на эти точки силами, называют системой свободных точек. Примером системы свободных точек может служить Солнечная система, планеты которой рассматривают в астрономии как материальные точки. Планеты свободно перемещаются по орбитам, зависящим от действующих на них сил.

Система материальных точек, движения которых ограничиваются наложенными на точки связями, называется системой несвободных точек. Примером системы несвободных точек может служить любой механизм или машина, у которых движения отдельных элементов ограничены связями.

Материальное тело мы также будем рассматривать как систему материальных частиц (точек), образующих это тело.

Механическая система с неголономными связями называется неголономной системой.

Механическая система с голономными связями называется голономной системой.

Известно, что механическое действие связей на точки системы выражается силами, называемыми реакциями связей. Таким образом, все силы, действующие на систему несвободных точек, можно разделить на задаваемые (активные) силы и реакции связей.

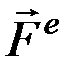
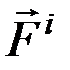
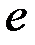
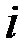
Внешними называются силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной системы. Внутренними называются силы, действующие на точки системы со стороны других точек или тел этой же системы. Будем обозначать внешние силы символом , а внутренние – (индексы и происходят от начальных букв французских слов: exterieur – внешний и interieur – внутренний).

Как внешние, так и внутренние силы могут быть, в свою очередь, или активными, или реакциями связей. Разделение сил на внешние и внутренние является условным и зависит от того, движение какой системы тел мы рассматриваем.

Таким образом, любая сила, действующая на точку механической системы в соответствии с приведёнными двумя классификациями сил, является внешней пли внутренней. В то же время она является задаваемой силой или реакцией связи. Движение точек механической системы зависит как от внешних, так и от внутренних сил.

Внутренние силы обладают следующими свойствами.

1. Геометрическая сумма (главный вектор) всех внутренних сил системы равняется нулю. По третьему закону динамики, любые две точки системы (рис. 15) действуют друг на друга с равными по модулю и противоположно направленными силами и ,сумма которых равна нулю. Так как аналогичный результат имеет место для любой пары точек системы, то

. (5.1)

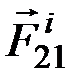
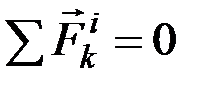
2. Сумма моментов (главный момент) всех внутренних сил системы относительно любого центра или оси равняется нулю.

Действительно, если взять произвольный центр ,то из рис. 15 видно, что

.

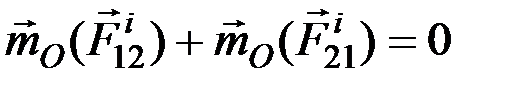
Аналогичный результат получится при вычислении моментов относительно оси. Следовательно, и для всей системы будет выполняться условие:

или . (5.2)

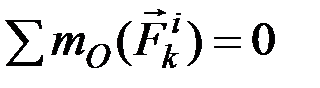
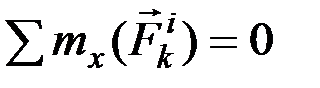
Из доказанных свойств не следует, что внутренние силы взаимно уравновешиваются и не влияют на движение системы, так как эти силы приложены к разным материальным точкам или телам и могут вызвать взаимные перемещения этих точек или тел. Уравновешенными внутренние силы будут тогда, когда рассматриваемая система представляет собою абсолютно твёрдое тело.

Центр масс. Движение системы, кроме действующих сил, зависит от ее суммарной массы и распределения масс. Масса системы равна арифметической сумме масс всех точек или тел, образующих систему:

.

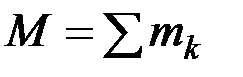
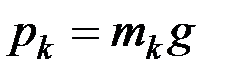
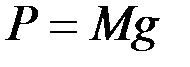
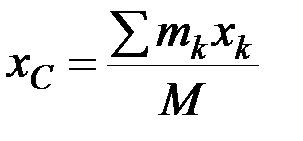
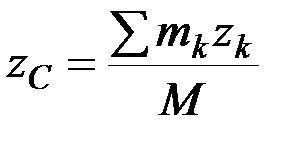
В однородном поле тяжести, для которого g = const, вес любой частицы тела будет пропорционален ее массе. Поэтому о распределении масс в теле можно судить по положению его центра тяжести. Преобразуем формулы, определяющие координаты центра тяжести (см. Алексеев В. В. Теоретическая механика. Статика. – Новосибирск, 2008), к виду, явно содержащему массу. Для этого положим , , после чего, сократив на ,получим:

, , . (5.3)

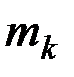
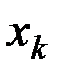
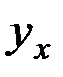
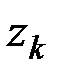
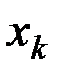
В полученные равенства входят только массы материальных точек (частиц), образующих тело, и координаты , , этих точек. Следовательно, положение точки действительно характеризует распределение масс в теле или в любой механической системе, если под , , , понимать соответственно массы и координаты точек этой системы.

Геометрическая точка 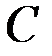, координаты которой определяются формулами (5.3), называется центром масс или центром инерции механической системы.

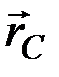
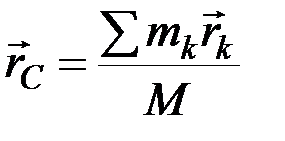
Если положение центра масс определять его радиус-вектором ,то для его определения используется формула:

, (5.4)

где – радиусы-векторы точек, образующих систему.

Хотя положение центра масс совпадает с положением центра тяжести тела, находящегося в однородном поле тяжести, понятия эти не являются тождественными. Понятие о центре тяжести как о точке, через которую проходит линия действия равнодействующей сил тяжести, по существу имеет смысл только для твёрдого тела, находящегося в однородном поле тяжести. Понятие же о центре масс как о характеристике распределения масс в системе имеет смысл для любой системы материальных точек или тел, причем это понятие сохраняет свой смысл независимо от того, находится ли данная система под действием каких-нибудь сил или нет.

Источник

Динамика:Законы Ньютона; силы, виды сил и их разложение, масса. Центр масс системы материальных точек.

Й билет

Кинематикой называют раздел механики, в котором движение тел рассматривается без
выяснения причин, его вызывающих.

Системой отсчета в физике называют совокупность тела отсчета, системыкоординат, связанной с телом отсчета, и часы или иной прибор для отсчета времени.
В Международной системе единиц (СИ) за единицу длины принят метр, а за единицу времени –
секунда.
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение
тела с его последующим положением.Перемещение есть векторная величина.

Ско́рость — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчета
Ускорение – это физическая величина, численно равная изменению скорости за единицу времени.

Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой _n.

Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:

Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t.
Путь – скалярная величина. Путь — это расстояние, которое прошло тело.

2. Виды движения (определения, формулы и графики )

1) Равномерное движение

Равномерное движение материальной точки — это движение, при котором величина скорости точки остаётся неизменной. Расстояние, пройденное точкой за время , задаётся в этом случае формулой .

— начальная координата точки, — проекция вектора скорости на координатную ось

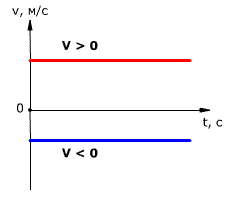
Зависимость проекции скорости тела от времени при равномерном прямолинейном движении

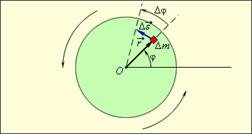
Для кинематического описания вращения твердого тела удобно использовать угловые величины: угловое перемещение Δϕ, угловую скорость ω

и угловое ускорениеε

При вращении твердого тела относительно неподвижной оси все его точки движутся с одинаковыми угловыми скоростями и одинаковыми угловыми ускорениями.

При малых угловых перемещениях Δφ модуль вектора ∆S линейного перемещения некоторого элемента массы Δm вращающегося твердого тела выражается соотношением:

где r – модуль радиус-вектора r υ = rω,

a = a_τ = rε.

Движение называется равноускоренным при а↑↑ν и равнозамедленным при а↑↓ν

Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, тоуравнение движения тела будет выглядеть следующим образом:

= ₀ + t

Вращение называется равнопеременным, если угловое ускорение тела в процессе движения остается постоянным по модулю и направлению

Чтобы найти закон изменения угловой скорости в этом случае, проинтегрируем левую часть равенства в пределах от до , а правую часть от 0 до t:

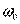
закон равнопеременного вращения:

Касательное ускорение:
a_t = εR

Закон сохранения импульса

Совокупность материальных точек (тел), рассматриваемых как единое целое, называется механической системой. Силы взаимодействия между материальными точками механической системы называются внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют внешние силы (они взаимно уравновешиваются), называется замкнутой или изолированной. В такой системе необходимо учитывать только силы взаимодействия между входящими в нее телами (внутренние силы). Строго говоря, изолированных механических систем в природе не существует.
Рассмотрим изолированную механическую систему, состоящую из n тел с массами m₁, m₂, …, m_n. Обозначим скорости этих тел через v₁, v₂, …, v_n а внутреннюю силу, действующую на i-е тело со стороны k-го,- через F_ik.

Складывая почленно эти уравнения и группируя силы F_ik и F_ki, получим:

Векторная сумма представляет собой импульс всей системы. Таким образом, или
(2.9)

Выражение (2.9) представляет собой закон сохранения импульса: импульс замкнутой системы тел с течением времени не изменяется.
Закон сохранения импульса справедлив не только в классической механике; он выполняется и для замкнутых систем микрочастиц, т.е. действует и в квантовой механике. Другими словами, этот закон носит универсальный характер и являетсяфундаментальным законом природы.
Закон сохранения импульса является следствием однородности пространства: при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства и законы движения не изменяются, т.е. не зависят от выбора положения начала координат инерциальной системы отсчета.
В классической механике из-за независимости массы от скорости импульс системы можно выразить через скорость ее центра масс.
Скорость i-й материальной точки связана с ее радиусом-вектором r_i соотношением:

Центром масс или центром инерции системы материальных точек называется воображаемая тоска С, положение которой характеризует распределение массы этой системы. Ее радиус-вектор равен

где масса системы.
Скорость центра масс определяется выражением:

т.е.
(2.10)

Другими словами, импульс системы равен произведению массы системы на скорость ее центра инерции.
Подставив выражение (2.10) в (2.9), получим:

т.е. в изолированной механической системе центр масс находится в покое или движется равномерно и прямолинейно.
Если система незамкнутая (на нее действуют помимо внутренних и внешние силы), то выражение (2.9) с учетом (2.10) запишется следующим образом:

или
(2.11)

где ускорение центра масс.
Из (2.11) вытекает закон (теорема) движения центра масс: центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, приложенных к системе.

Й билет

Моментом импульса материальной точки относительно некоторой точки О называется вектор , равный векторному произведению радиус-вектора материальной точки относительно точки О на импульс материальной точки

Модуль момента импульса

Направление момента импульса определяется по правилу правого винта (вектора и составляют правую тройку векторов).

Момент импульса системы материальных точек равен векторной сумме моментов импульсов отдельных материальных точек системы или векторному произведению радиус-вектора центра масс системы на импульс ее центра масс

Величина момента импульса твердого тела относительно оси вращения

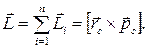
Изотропность пространства (осевая симметрия пространства) приводит к закону сохранения момента импульса: в замкнутых системах момент импульса сохраняется.

7. Основной закон динамики вращательного движения.

Основной закон динамики вращательного движения можно получить из второго закона Ньютона для поступательного движения твердого тела

где m_i – масса i-й точки; – угловое ускорение; r_i – ее расстояние до оси вращения.

– момент инерции i-й материальной точки.

Мгновенное значение углового ускорения , есть первая производная угловой скорости по времени , то есть

или , где – импульс момента силы – это произведение момента силы на промежуток времени

– изменение момента импульса тела, – момент импульса тела есть произведение момента инерции J на угловую скорость , а есть .

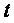
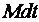
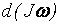
Поэтому основной закон динамики вращательного движения твердого тела формулируется так: “Импульс момента силы , действующий на вращательное тело, равен изменению его момента импульса ”:

или

Электростатическое поле. Поле точечного заряда ( напряженность, потенциал, работа по переносу заряда в эл. поле, графическое представление поля ). Закон Кулона. Принцип суперпозиции электрических полей

Электрическое поле — пространство, обладающее свойством действовать с силой на электрический заряд, помещённый в это поле.

Напряженность электрического поля

где: F — сила, действующая на точечный положительный заряд Q, помещенный в данную точку поля.

Сила, действующая на точечный заряд Q, помещенный в электрическое поле:

Поток вектора напряженности Е электрического поля:

а) через произвольную поверхность S, помещенную в неоднородное поле,

или

где: a — угол между вектором напряженности Е и нормалью n к элементу поверхности;

dS — площадь элемента поверхности;

E_n — проекция вектора напряженности на нормаль;

б) через плоскую поверхность, помещенную в однородное электрическое поле,

Поток вектора напряженности Е через замкнутую поверхность:

где интегрирование ведется по всей поверхности.

1. Начинаются на положительных и заканчиваются на отрицательных зарядах.

3. Густота линий тем больше, чем больше напряженность. Т.е. напряженность поля прямо пропорциональна количеству силовых линий, проходящих через единицу площади поверхности.

4. Можно договориться изображать поля так, что количество проведенных линий пропорционально величине заряда.

Потенциал электрического поля есть величина, равная отношению потенциальной энергии точечного положительного заряда, помещенную в данную точку поля, к этому заряду;

или потенциал электрического поля есть величина, равная отношению работы сил поля по перемещению точечного положительного заряда из данной точки поля в бесконечность к этому заряду:

Потенциал электрического поля в бесконечности условно принят равным нулю.

Работа, совершаемая электрическим полем при перемещении точечного заряда Q из одной точки поля, имеющей потенциал j₁, в другую, имеющую потенциал j₂,

где: E_l — проекция вектора напряженности Е на направление перемещения;

В случае однородного поля последняя формула принимает вид

где: l — перемещение;

a — угол между направлениями вектора Е и перемещения l.

Модуль силы взаимодействия двух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними.

где: F — сила взаимодействия двух точечных зарядов Q₁, и Q₂;

r — расстояние между зарядами;

e — диэлектрическая проницаемость среды;

e₀ — электрическая постоянная:

Если поле в некоторой точке пространства создаётся отдельными точечными зарядами, то напряжённость результирующего поля Е равна векторной сумме напряженностей складываемых полей

Это правило получило название принципа суперпозиции электрических полей-результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.. Подчеркнем ещё раз, что справедливость этого принципа подтверждена экспериментально.

26. Циркуляция вектора напряженности электрического поля. Связь напряженности и потенциала эл. поля

27. Теорема Гаусса для электрического поля и примеры её применения

28. Поле диполя. Диполь в однородном и неоднородном электрическом поле

Законы Ома.

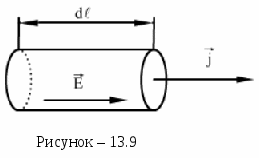
Закон Джоуля-Ленца в дифференциальноё форме-Мощность тепла, выделяемого в единице объёма среды при протекании постоянного электрического тока, пропорциональна произведению плотности электрического тока на величину напряженности электрического поля

Выделим в проводнике элементарный цилиндрический объём dV=dSdℓ (ось цилиндра совпадает с направлением тока(рис.13., сопротивление которого . По закону Джоуля-Ленца, за время в этом объёме выделится теплота Количество теплоты, выделившееся за единицу времени в единице объёма, называется удельной тепловой мощностью тока. Она равна ω= ρ∙j 2 Используя дифференциальную форму закона Ома (j = γE) и соотношение , получим ω= j∙E=γ∙E 2

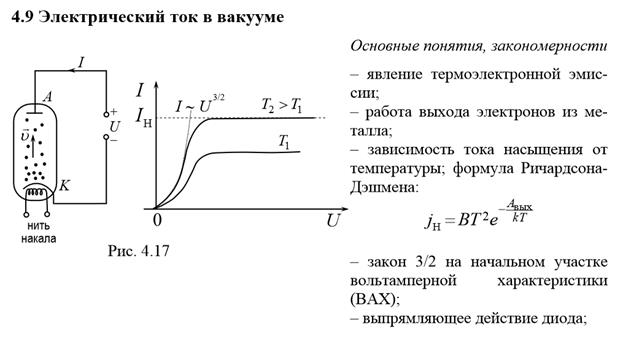
Электрический ток в вакууме

Под термоэлектронной эмиссией следует понимать процесс испускания электронов нагретыми телами, обычно в вакуум или газовую среду.

Чтобы электрон мог выйти из металла за его пределы, должна быть совершена определенная работа А против этих сил, которая получила название работа выхода электрона из металла. A_вых = eφ

Ток насыщения характеризует эмиссионную способность катода, которая зависит от природы катода и его температуры. Он растёт с повышением температуры катода. Зависимость тока насыщения от температуры катода выражается формулой Ричардсона-Дешмена:

Эффект Холла.

42. Закон Био-Савара-Лапласа и примеры его применения.

Формулировка закона Био Савара Лапласа имеет вид: При прохождении постоянного тока по замкнутому контуру, находящемуся в вакууме, для точки, отстоящей на расстоянии r0, от контура магнитная индукция будет иметь вид.

43. Закон полного тока для магнитного поля в вакууме и примеры его применения. Вихревой характер магнитных полей.

Вихревые токи ( токи Фуко).

Й билет

Кинематикой называют раздел механики, в котором движение тел рассматривается без
выяснения причин, его вызывающих.

Системой отсчета в физике называют совокупность тела отсчета, системыкоординат, связанной с телом отсчета, и часы или иной прибор для отсчета времени.
В Международной системе единиц (СИ) за единицу длины принят метр, а за единицу времени –
секунда.
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение
тела с его последующим положением.Перемещение есть векторная величина.

Ско́рость — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчета
Ускорение – это физическая величина, численно равная изменению скорости за единицу времени.

Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой _n.

Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:

Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t.
Путь – скалярная величина. Путь — это расстояние, которое прошло тело.

2. Виды движения (определения, формулы и графики )

1) Равномерное движение

Равномерное движение материальной точки — это движение, при котором величина скорости точки остаётся неизменной. Расстояние, пройденное точкой за время , задаётся в этом случае формулой .

— начальная координата точки, — проекция вектора скорости на координатную ось

Зависимость проекции скорости тела от времени при равномерном прямолинейном движении

Для кинематического описания вращения твердого тела удобно использовать угловые величины: угловое перемещение Δϕ, угловую скорость ω

и угловое ускорениеε

При вращении твердого тела относительно неподвижной оси все его точки движутся с одинаковыми угловыми скоростями и одинаковыми угловыми ускорениями.

При малых угловых перемещениях Δφ модуль вектора ∆S линейного перемещения некоторого элемента массы Δm вращающегося твердого тела выражается соотношением:

где r – модуль радиус-вектора r υ = rω,

a = a_τ = rε.

Движение называется равноускоренным при а↑↑ν и равнозамедленным при а↑↓ν

Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, тоуравнение движения тела будет выглядеть следующим образом:

= ₀ + t

Вращение называется равнопеременным, если угловое ускорение тела в процессе движения остается постоянным по модулю и направлению

Чтобы найти закон изменения угловой скорости в этом случае, проинтегрируем левую часть равенства в пределах от до , а правую часть от 0 до t:

закон равнопеременного вращения:

Касательное ускорение:
a_t = εR

Динамика:Законы Ньютона; силы, виды сил и их разложение, масса. Центр масс системы материальных точек.

Динамикой называют раздел механики, в котором изучают различные виды механических движений с учетом взаимодействия тел между собой. Основы динамики составляют три закона Ньютона, являющиеся результатом обобщения наблюдений и опытов в области механических явлений, которые были известны еще до Ньютона и осуществлены самим Ньютоном.

Законы динамики Ньютона (иначе называемой классической динамикой) имеют ограниченную область применимости. Они справедливы для макроскопических тел, движущихся со скоростями, много меньшими, чем скорость света в вакууме.Динамика оперирует такими понятиями, как масса,сила, импульс, момент импульса, энергия..

К выводу о существовании явления инерции впервые пришел Галилей, а затем Ньютон. Этот вывод формулируется в виде первого закона Ньютона (закона инерции): существуют такие системы отсчета, относительно которых тело (материальная точка) при отсутствии на нею внешних воздействий (или при их взаимной компенсации) сохраняет состояние покоя или равномерного прямолинейного движения.

Системы отсчета, в которых выполняется первый закон Ньютона, называют инерциальными. Следовательно, инерциальными являются такие системы отсчета, относительно которых материальная точка при отсутствии на нее внешних воздействий или их взаимной компенсации покоится или движется равномерно и прямолинейно.

Источник