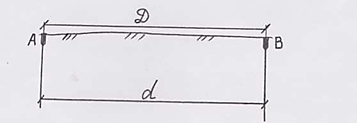Что называется масштабом в геодезии
Масштаб
Понятие наиболее распространено в геодезии, картографии и проектировании — отношение натуральной величины объекта к величине его изображения. Человек не в состоянии изобразить большие объекты, например, дом, в натуральную величину, поэтому, при изображении большого объекта в рисунке, чертеже, макете и так далее, человек уменьшает величину объекта в несколько раз: в два, пять, десять, сто, тысяча и так далее. Число, показывающее, во сколько раз уменьшен изображенный объект, есть масштаб. Масштаб применяется и при изображении микромира. Человек не может изобразить живую клетку, которую рассматривает в микроскоп, в натуральную величину и поэтому увеличивает величину ее изображения в несколько раз. Число, показывающее, во сколько раз произведено увеличение или уменьшение реального явления при его изображении, определено как масштаб.
Содержание
Масштаб в геодезии, картографии и проектировании
Масштаб показывает, во сколько раз каждая линия, нанесенная на карту или чертёж, меньше или больше её действительных размеров. Есть три вида масштаба: численный, именованный, графический.
Масштабы на картах и планах могут быть представлены численно или графически.
Численный масштаб записывают в виде дроби, в числителе которой стоит единица, а в знаменателе — степень уменьшения проекции. Например, масштаб 1:5 000 показывает, что 1 см на плане соответствует 5 000 см (50 м) на местности.
Более крупным является тот масштаб, у которого знаменатель меньше. Например, масштаб 1:1 000 крупнее, чем масштаб 1:25 000.
Графические масштабы подразделяются на линейные и поперечные. Линейный масштаб — это графический масштаб в виде масштабной линейки, разделённой на равные части. Поперечный масштаб — это графический масштаб в виде номограммы, построение которой основано на пропорциональности отрезков параллельных прямых, пересекающих стороны угла.Поперечный масштаб применяют для более точных измерений длин линий на планах. Поперечным масштабом пользуются следующим образом: откладывают на нижней линии поперечного масштаба замер длины таким образом, чтобы один конец (правый) был на целом делении ОМ, а левый заходил за 0. Если левая ножка попадает между десятыми делениями левого отрезка (от 0), то поднимаем обе ножки измерителя вверх, пока левая ножка не попадёт на пересечение к-либо трансвенсали и какой-либо горизонтальной линии. При этом правая ножка измерителя должна находиться на этой же горизонтальной линии. Наименьшая ЦД = 0,2 мм, а точность — 0,1.
Точность масштаба — это отрезок горизонтального проложения линии, соответствующий 0,1 мм на плане. Значение 0,1 мм для определения точности масштаба принято из-за того, что это минимальный отрезок, который человек может различить невооруженным глазом. Например, для масштаба 1:10 000 точность масштаба будет равна 1 м. В этом масштабе 1 см на плане соответствует 10 000 см (100 м) на местности, 1 мм — 1 000 см (10 м), 0,1 мм — 100 см (1 м).
Масштабы изображений на чертежах должны выбираться из следующего ряда: [1]
| Масштабы уменьшения | 1:2; 1:2,5; 1:4; 1:5; 1:10; 1:15; 1:20; 1:25; 1:40; 1:50; 1:75; 1:100; 1:200; 1:400; 1:500; 1:800; 1:1 000 |
| Натуральная величина | 1:1 |
| Масштабы увеличения | 2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100:1 |
При проектировании генеральных планов крупных объектов допускается применять масштабы 1:2 000; 1:5 000; 1:10 000; 1:20 000; 1:25 000; 1:50 000.
В необходимых случаях допускается применять масштабы увеличения (100n):1, где n — целое число.
Масштаб в фотографии
При фотосъёмке под масштабом понимают отношение линейного размера изображения, полученного на фотоплёнке или светочувствительной матрице, к линейному размеру проекции соответствующей части сцены на плоскость, перпендикулярную к направлению на камеру.
Некоторые фотографы измеряют масштаб как отношение размеров объекта к размерам его изображения на бумаге, экране или ином носителе. Правильная методика определения масштаба зависит от контекста, в котором используется изображение.
Масштаб имеет важное значение при расчете глубины резко изображаемого пространства. Фотографам доступен очень широкий диапазон масштабов — от практически бесконечно малого (например, при съемке небесных тел) до очень крупного (без использования специальной оптики возможно получение масштабов порядка 10:1).
Под макрофотографией традиционно понимают съёмку в масштабе 1:1 или крупнее. Однако с широким распространением компактных цифровых фотоаппаратов этим термином стали также называть съёмку расположенных близко к объективу (как правило, ближе 50 см) мелких объектов. Связано это с необходимым изменением режима работы системы автофокуса в таких условиях, однако с точки зрения классического определения макросъёмки такое толкование является неверным.
Масштаб в моделизме
Для каждого вида масштабного (стендового) моделизма определены масштабные ряды, состоящие из нескольких масштабов разной степени уменьшения, причём для разных видов моделизма (авиамоделизм, судомоделизм, железнодорожный, автомобильный, военной техники) определены свои, исторически сложившиеся, масштабные ряды, которые обычно не пересекаются.
Масштаб в моделизме исчисляется по формуле:
При масштабе 1/72, и параметре оригинала 7500 мм, решение будет выглядеть;
7500 мм / 72 = 104,1 мм
Полученное значение 104,1 мм, есть искомое значение при масштабе 1/72
Масштаб времени
В программировании
В операционных системах с разделением времени чрезвычайно важную роль играет предоставление отдельно взятым задачам так называемого «режима реального времени», при котором обработка внешних событий обеспечивается без дополнительных задержек и пропусков. Для этого употребляется также термин «реальный масштаб времени», однако это терминологическая условность, не имеющая к исходному значению слова «масштаб» никакого отношения.
В кинотехнике
Масштаб времени — количественная мера замедления или ускорения движения, равная отношению проекционной частоты кадров к съёмочной. Так, если проекционная частота кадров равна 24 кадра в секунду, а киносъёмка производилась на 72 кадра в секунду, масштаб времени равен 1:3. Масштаб времени 2:1 означает ускоренное вдвое по сравнению с обычным протекание процесса на экране.
В математике
Масштабы изображений на чертежах должны выбираться из следующего ряда (масштабы ГОСТ 2.302-68): Масштабы уменьшения 1 : 2; 1 : 2,5; 1 : 4; 1 : 5; 1 : 10; 1 : 15; 1 : 20; 1 : 25; 1 : 40; 1 : 50; 1 : 75; 1 : 100; 1 : 200; 1 : 400; 1 : 500; 1 : 800; 1 : 1000 Натуральная величина 1 : 1 Масштабы увеличения 2 : 1; 2.5,5 : 1; 4 : 1; 5 : 1; 10 : 1; 20 : 1; 40 : 1; 50 : 1; 100: 1 см. например Быстро-медленная система
Масштаб-число,показывающее, во сколько раз уменьшены или увеличены настоящие размеры на чертеже.
Лекция на тему: Масштабы
1. Понятие о масштабах
2. Теория построения поперечного масштаба
Просмотр содержимого документа
«Лекция на тему: Масштабы»
1. Понятие о масштабах.
При измерении линий на местности измеряется их наклонная длина. На план или карту наносят проекции этих линий на горизонтальную плоскость уменьшенные в несколько сотен или тысяч раз..
Линия не имеет наклона – ее проекция будет равна измеренной длине.
ν – угол наклона линии.
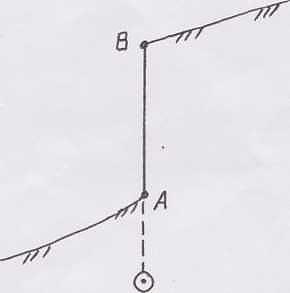
Линия имеет наклон 90 0 – в этом случае проекция линии превращается в точку.
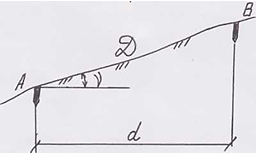
Линия имеет угол наклона от 0 0 до 90 0
d = D* cos ν ( при 0 0 ν 0 )
Проекция линии на горизонтальной плоскости называется ее горизонтальным проложением.
В соответствии с основными целями геодезии и ее задачами в землеустройстве, снимаемая территория наносится на план или карту всегда с определенной степенью уменьшения.
В геодезии применяются следующие виды масштабов:
1. численный ( применяется всегда)
2. именованный (словесный) масштаб
3.линейный ( применяются для удобства и повышения скорости обработки материалов съемок).
5. масштаб шагов ( применяется при глазомерных съемках).
МАСШТАБ – это степень уменьшения, выраженная отношением длины отрезка линии на плане (профиле) к соответствующей ей проекции на местности.
Численный масштаб – это дробь, у которой числитель, равный единице, показывает длину отрезка на плане (профиле), а знаменатель – соответствующую ей длину проекции отрезка на местности.
В зависимости от величины знаменателя различают мелкие и крупные масштабы, чем больше знаменатель, тем мельче масштаб и наоборот.
Именованный масштаб выражается именованными числами, обозначающими длины взаимно соответствующих отрезков на карте и в натуре.
— в 1 сантиметре 5 километров (в 1 см 5 км).
Линейный масштаб – это график, построенный для работы с данной картой по ее численному масштабу.
График имеет вид прямой, разделенной на равные отрезки ( основания). Слева от нуля графика оставляют один отрезок и делят его 10 частей.
Вправо от нуля в конце каждого отрезка надписывают числа метров местности соответствующие расстояниям концов от нуля.
Рис.4 Линейный масштаб
Длина отрезка, который откладывают по линии при построении масштаба, называется его основанием.
Поперечный масштаб строится для точности работы с планом или картой, при чем график является универсальным, т.е. имея этот график можно работать с любой картой или планом.
Наименьшее деление поперечного масштаба t = 0,01 основания.
Невооруженным глазом при нормальном зрении можно различать точки, удаленные друг от друга на 0,01 см или 0,1мм. Расстояние на местности, которое соответствует 0,01 см на плане, называется точностью масштаба.
2. Теория и построение поперечного масштаба, его точность.
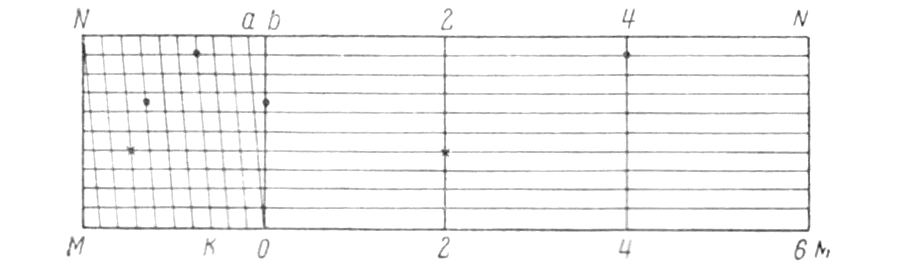
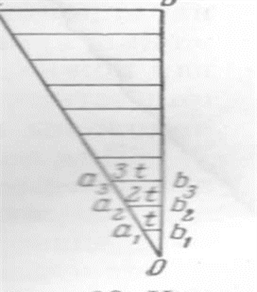
2.1 Построение поперечного масштаба. При пользовании простым линейным масштабом приходится мелкие доли в крайнем левом основании отсчитывать на глаз. Чтобы эти отсчеты были более точными и надежными, употребляют особых вид линейного масштаба, который называется поперечным. Для получения поперечного масштаба сначала выполняют на горизонтальной линии ММ построение простого линейного масштаба. Затем из концов отложенных оснований восстанавливают вверх от линии ММ перпендикуляры МN, ob, 2—2 и т. д.
Левые нижние и верхние основания Мо и Nb делят на 10 равных частей и точки деления соединяют, как показано на рисунке, косыми линиями, называемыми-трансверсалями.
Рис. 5 Поперечный масштаб
Полученный чертеж и называется поперечным масштабом. Из построения его следует, что расстояния между соседними трансверсалями по параллелям равны 0.1 ℓ. Расстояния же от перпендикуляра ob до первой трансверсали оа при переходе от параллели к параллели изменяются.
Здесь по построению ab =0,1 ℓ и оb1: оb=0,1; следовательно.
т. е. наименьшее деление поперечного масштаба составляет 0,01 основания масштаба.
и т. д., т. е. при переходе вверх с параллели на соседнюю параллель расстояния от перпендикуляра оb до первой трансверсали увеличиваются на величину наименьшего деления. Очевидно, что точки пересечения любой трансверсали с параллелями при переходе с параллели на параллель вверх сдвигаются влево от перпендикулярного положения на ту же величину. Описанный поперечный масштаб называется сотенным или нормальным.
Теоретически при построении поперечного масштаба можно как первое левое основание, так и расстояние вверх по перпендикулярам делить не обязательно на 10, а на какое угодно другое число равных частей. Разница будет только в том, что наименьшее деление его будет составлять другую долю от основания. Обозначим в общем виде число частей основания буквой т и число частей, отложенных по перпендикуляру вверх, буквой п. В таком случае наименьшее деление выразится формулой:
2.2 Пользование поперечным масштабом.
Для практического использования на заводах изготовляют специальные металлические масштабные линейки, на которых с помощью особых делительных машин гравируют нормальные поперечные масштабы с основанием 2 см. Подписи на них дают в сантиметрах. На рисунке 5 изображена левая часть такого масштаба. В конце правой части гравируют также пятидесятенный масштаб, у которого основание разделено на 5 равных частей, так что по нему можно непосредственно учитывать 0,02 основания, т. е. 0,04 см.
Пользование поперечным масштабом непосредственно вытекает из его теории. Пусть, например, требуется взять в раствор измерителя 4,78 см. На нижней горизонтальной линии ММ непосредственно можно взять расстояние 4.60 см (расстояние 4 — к). Для заданного отсчета это расстояние нужно увеличить на 0,18 см, для чего левая ножка измерителя должна быть передвинута по трансверсали к вверх на девятую параллель (так как 0,18 =0,02*9). На этой параллели ножки измерителя устанавливают в точки, отмеченные на рисунке кружками. Крестиками на 4-й параллели отмечено расстояние 3,48 см. Практически ножки измерителя можно устанавливать на глаз посредине между параллелями и таким образом учитывать сотые доли сантиметра. Например, если ножки поставить посредине между 6-й и 7-й параллелями, как отмечено на рисунке точками, то взятое расстояние будет 1.33 см.
Для измерения линии, начерченной на бумаге, ее берут в раствор измерителя и прикладывают его к масштабу так, чтобы левая ножка находилась в пределах крайнего левого основания, а правая все время точно совмещалась с каким-либо перпендикуляром правее нуля. Передвигая в этом положении измеритель вверх, добиваются, чтобы левая ножка точно совместилась с пересечением ближайшей левой от нее трансверсали с некоторой параллелью, на которой должна находиться и правая ножка. В этом положении производят отсчеты: по перпендикуляру, с которым совмещена правая ножка, целые сантиметры, по нижним делениям крайнего левого основания четные десятые доли сантиметра и по номеру параллели, на которой расположены ножки измерителя, четные сотые доли сантиметра.
Для перехода от длин линий на местности к длинам их на плане и обратно поперечные масштабы подписываются, как было указано для простых линейных масштабов. Если при переходах пользоваться масштабной линейкой, то предварительно следует установить значения его делений в соответствии с численным масштабом. Например, для масштаба 1 : 25 000 основание составит 500 м, деления крайнего левого основания будут по 50м и наименьшее деление масштаба — 5 м.
3. Способы определения длин линий, измеренных на плане
Чтобы определить по карте расстояние между точками местности (предметами, объектами), пользуясь численным масштабом, надо измерить на карте расстояние между этими точками в сантиметрах и умножить полученное число на величину масштаба.
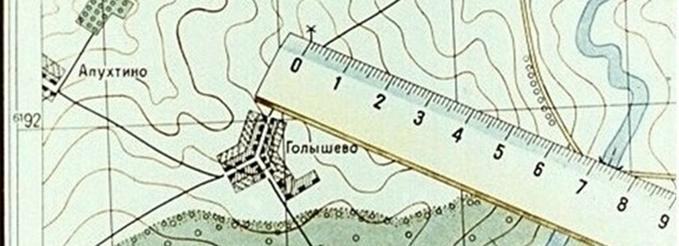
Пример, на карте масштаба 1:25000 измеряем линейкой расстояние между мостом и ветряной мельницей (рис. 7); оно равно 7,3 см, умножаем 250 м на 7,3 и получаем искомое расстояние; оно равно 1825 метров (250х7,3=1825).
Рис. 7. Определение по карте расстояние между точками местности с помощью линейки.
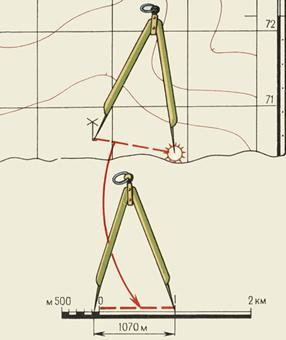
Небольшое расстояние между двумя точками по прямой линии проще определить, пользуясь линейным масштабом (рис. 8). Для этого достаточно циркуль-измеритель, раствор которого равен расстоянию между заданными точками на карте, приложить к линейному масштабу и снять отсчет в метрах или километрах. На рис. 3 измеренное расстояние равно 1070 м.
Рис. 8. Измерение на карте расстояний циркулем-измерителем по линейному масштабу
Рис. 9. Измерение на карте расстояний циркулем-измерителем по извилистым линиям
Большие расстояния между точками по прямым линиям измеряют обычно с помощью длинной линейки или циркуля-измерителя.
В первом случае для определения расстояния по карте с помощью линейки пользуются численным масштабом (см. рис. 7).
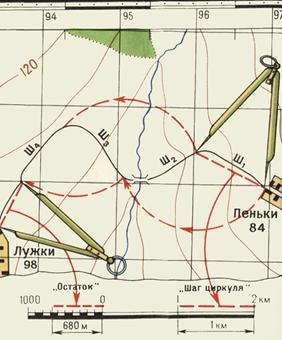
Во втором случае раствор «шаг» циркуля-измерителя устанавливают так, чтобы он соответствовал целому числу километров, и на измеряемом по карте отрезке откладывают целое число «шагов». Расстояние, не укладывающееся в целое число «шагов» циркуля-измерителя, определяют с помощью линейного масштаба и прибавляют к полученному числу километров.
Таким же способом измеряют расстояния по извилистым линиям (рис. 9). В этом случае «шаг» циркуля-измерителя следует брать 0,5 или 1 см в зависимости от длины и степени извилистости измеряемой линии.
Рис. 10. Измерения расстояния курвиметром
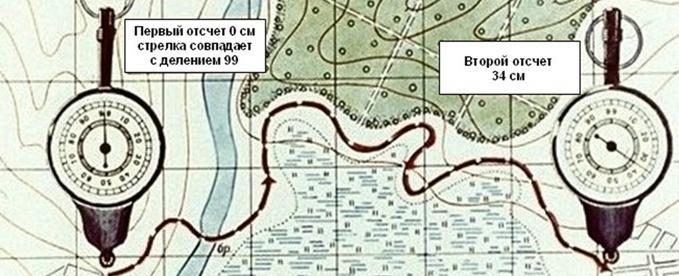
Для определения длины маршрута по карте применяют специальный прибор, называемый курвиметром (рис. 10), который особенно удобен для измерения извилистых и длинных линий.
В приборе имеется колесико, которое соединено системой передач со стрелкой.
При измерении расстояния курвиметром нужно установить его стрелку на деление 99. Держа курвиметр в вертикальном положении вести его по измеряемой линии, не отрывая от карты вдоль маршрута так, чтобы показания шкалы возрастали. Доведя до конечной точки, отсчитать измеренное расстояние и умножить его на знаменатель численного масштаба. (В данном примере 34х25000=850000, или 8500 м)
Точность измерения расстояний по карте. Поправки на расстояние за наклон и извилистость линий.
Точность определения расстояний по карте зависит от масштаба карты, характера измеряемых линий (прямые, извилистые), выбранного способа измерения, рельефа местности и других факторов.
Наиболее точно определить расстояние по карте можно по прямой линии.
В горных районах при большой крутизне скатов ошибки будут больше. Это объясняется тем, что при съемке местности на карту наносят не длину линий на поверхности Земли, а длину проекций этих линий на плоскость.
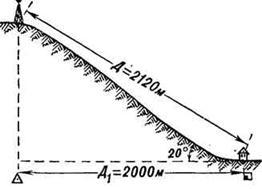
Например, При крутизне ската 20° (рис. 11) и расстоянии на местности 2120 м его проекция на плоскость (расстояние на карте) составляет 2000 м, т. е. на 120 м меньше.
Рис. 11. Проекция длины ската на плоскость (карту)
При определении длины маршрута по карте следует учитывать, что расстояния по дорогам, измеренные на карте с помощью циркуля или курвиметра, в большинстве случаев получаются короче действительных расстояний.
Это объясняется не только наличием спусков и подъемов на дорогах, но и некоторым обобщением извилин дорог на картах.
Поэтому получаемый по карте результат измерения длины маршрута следует с учетом характера местности и масштаба карты умножить на коэффициент, указанный в таблице.
Простейшие способы измерения площадей по карте.
Более точно площади измеряют палеткой, представляющей собой лист прозрачного пластика с нанесенной на него сеткой квадратов со стороной 10 мм (в зависимости от масштаба карты и необходимой точности измерений).
Наложив такую палетку на измеряемый объект на карте, подсчитывают по ней сначала число квадратов, полностью укладывающихся внутри контура объекта, а затем число квадратов пересекаемых контуром объекта. Каждый из неполных квадратов принимаем за половину квадрата. В результате перемножения площади одного квадрата на сумму квадратов получают площадь объекта.
По квадратам масштабов 1:25000 и 1:50000 площади небольших участков удобно измерять офицерской линейкой, имеющей специальные вырезы прямоугольной формы. Площади этих прямоугольников <в гектарах ) указаны на линейке для каждого масштаба карты.
Масштабы топографических карт и планов
Понятие масштаба и его виды
Масштаб карты – это отношение длины отрезка на карте к его действительной длине на местности.
Масштаб (от немецкого Stab – палка) – это отношение длины отрезка на карте, плане, аэро- или космическом снимке к его действительной длине на местности.
Рассмотрим виды масштабов.
Численный масштаб
Это масштаб, выраженный в виде дроби, где числитель – единица, а знаменатель – число, показывающее во сколько раз уменьшено изображение.
Численный масштаб – масштаб, выраженный дробью, в которой:
Именованный (словесный) масштаб
Это вид масштаба, словесное указание того, какое расстояние на местности соответствует 1 см на карте, плане, снимке.
Именованный масштаб выражается именованными числами, обозначающими длины взаимно соответствующих отрезков на карте и в натуре.
Например, в 1 сантиметре 5 километров (в 1 см 5 км).
Линейный масштаб
Это вспомогательная мерная линейка, наносимая на карты для облегчения измерения расстояний.
Масштаб плана и масштаб карты
Масштаб плана одинаков во всех его точках.
Масштаб карты в каждой точке имеет свое частное значение, зависящее от широты и долготы данной точки. Поэтому его строгой числовой характеристикой является численный масштаб – отношение длины бесконечно малого отрезка Д на карте к длине соответствующего бесконечно малого отрезка на поверхности эллипсоида земного шара.
Однако при практических измерениях на карте используют её главный масштаб.
Формы выражения масштаба
Обозначение масштаба на картах и планах имеет три формы – численный, именованный и линейный масштабы.
Численный масштаб выражают дробью, в которой:
В России для топографических карт приняты стандартные численные масштабы
Основные масштабы топографических планов в России
При сравнении различных численных масштабов более мелким является тот, у которого больше знаменатель М, и, наоборот, чем меньше знаменатель М, тем крупнее масштаб плана или карты.
Так, масштаб 1:10000 крупнее, чем масштаб 1:100000, а масштаб 1:50000 мельче масштаба 1:10000.
Примечание
Применяемые в топографических картах масштабы установлены Приказом Министерства экономического развития РФ «Об утверждении требований к государственным топографическим картам и государственным топографическим планам, включая требования к составу сведений, отображаемых на них, к условным обозначениям указанных сведений, требования к точности государственных топографических карт и государственных топографических планов, к формату их представления в электронной форме, требований к содержанию топографических карт, в том числе рельефных карт» (№ 271 от 6 июня 2017 года с изменениями на 11 декабря 2017 года).
Именованный масштаб
Так как длины линий на местности принято измерять в метрах, а на картах и планах в сантиметрах, то масштабы удобно выражать в словесной форме, например:
В одном сантиметре 50 м. Это соответствует численному масштабу 1:5000. Поскольку 1 метр равен 100 сантиметрам, то число метров местности, содержащееся в 1 см карты или плана, легко определяют путём деления знаменателя численного масштаба на 100.
Линейный масштаб
Представляет собой график в виде отрезка прямой, разделенного на равные части с подписанными значениями соразмерных им длин линий местности. Линейный масштаб позволяет без вычислений измерять или строить расстояния на картах и планах.
Точность масштаба
Предельная возможность измерения и построения отрезков на картах и планах ограничена величиной 0.01 см. Соответствующее ей число метров местности в масштабе карты или плана представляет собой предельную графическую точность данного масштаба.
Масштабы топографических карт
численный масштаб карты
название карты
1 см на карте соответствует на местности расстоянию
1 см 2 на карте соответствует на местности площади
1:5 000
1:10 000
1:25 000
1:50 000
1:1100 000
1:200 000
1:500 000
пятисоттысячная, или полумиллионная
1:1000000
Ниже приведены численные маштабы карт и соответствующие им именованые масштабы:
Масштаб 1:100 000
Масштаб 1:10000
Масштаб 1:5000
Масштаб 1:2000
Масштаб 1:1000
Масштаб 1:500
Масштаб 1:200
Масштаб 1:100
Пример 1
Переведите численный масштаб карты в именованный:
Решение:
Для более легкого перевода численного масштаба в именованный нужно посчитать, на сколько нулей кончается число в знаменателе.
Например, в масштабе 1:500 000 в знаменателе после цифры 5 находится пять нулей.
Если после цифры в знаменателе пятьи более нулей, то, закрыв (пальцем, авторучкой или просто зачеркнув) пять нулей, получим число километров на местности, соответствующее 1 сантиметру на карте.
Пример для масштаба 1:500 000
В знаменателе после цифры – пять нулей. Закрыв их, получим для именованного масштаба: в 1 см на карте 5 километров на местности.
Если после цифры в знаменателе менее пяти нулей, то, закрыв два нуля, получим число метров на местности, соответствующее 1 сантиметру на карте.
Если, например, в знаменателе масштаба 1:10 000 закроем два нуля, получим:
Ответы:
Используйте линейку, накладывайте на карты для облегчения измерения расстояний.
Пример 2
Переведите именованный масштаб в численный:
Решение:
Для более легкого перевода именованного масштаба в численный нужно перевести расстояние на местности, указанное в именованном масштабе, в сантиметры.
Если расстояние на местности выражено в метрах, тогда чтобы получить знаменатель численного масштаба, нужно приписать два нуля, если в километрах, то пять нулей.
Например, для именованного масштаба в 1 см – 100 м расстояние на местности выражено в метрах, поэтому для численного масштаба приписываем два нуля и получаем: 1:10 000.
Для масштаба в 1 см – 5 км приписываем к пятерке пять нулей и получаем: 1:500 000.
Ответы:
Типы карт в зависимости от масштабов
Карты в зависимости от масштабов условно подразделяют на следующие типы:
Топографическая карта
Топографическими называются такие карты, содержание которых позволяет решать по ним разнообразные технические задачи.
Карты либо являются результатом непосредственной топографической cъемки местности, либо составляются по имеющимся картографическим материалам.
Местность на карте изображается в определенном масштабе.
Чем меньше знаменатель численного масштаба, тем крупнее масштаб. Планы составляют в крупных масштабах, а карты – в мелких.
В картах учитывается «шарообразность» земли, а в планах – нет. Из-за этого планы не составляются для территорий площадью свыше 400 км² (то есть участков земли примерно 20 км х 20 км).
В нашей стране приняты следующие масштабы топографических карт:
Этот ряд масштабов называется стандартным. Раньше этот ряд включал масштабы 1:300 000, 1:5000 и 1:2000.
В настоящее время существует методика создания топографических карт и планов любых масштабов, не имеющих грифа секретности и предназначенных для открытого пользования.
Сказка про карту в масштабе 1:1
Жил-был Капризный Король. Однажды он объехал своё королевство и увидел, как велика и прекрасна его земля. Он увидел извилистые реки, огромные озёра, высокие горы и чудесные города. Он возгордился своими владениями и захотел, чтобы весь мир узнал о них.
И вот, Капризный Король приказал картографам создать карту королевства. Картографы трудились целый год и, наконец, преподнесли Королю замечательную карту, на которой были обозначены все горные гряды, крупные города и большие озёра и реки.
Однако, Капризный Король остался недоволен. Он хотел видеть на карте не только очертания горных цепей, но и изображение каждой горной вершины. Не только крупные города, но и мелкие, и селения. Он хотел видеть небольшие речки, впадающие в реки.
Картографы вновь принялись за работу, трудились много лет и нарисовали другую карту, размером в два раза больше предыдущей. Но теперь Король пожелал, чтобы на карте были видны перевалы между горными вершинами, маленькие озерца в лесах, ручейки, крестьянские домики на окраине селений. Картографы рисовали все новые и новые карты.
Капризный Король умер, так и не дождавшись окончания работы. Наследники один за другим вступали на трон и умирали в свою очередь, а карта все составлялась и составлялась. Каждый король нанимал новых картографов для составления карты королевства, но всякий раз оставался недовольным плодами труда, находя карту недостаточно подробной.
Где же собирались хранить Капризные Короли свою замечательную карту? Ларца для такой карты не хватит. Понадобится огромное помещение вроде ангара, и в нем карта будет лежать во много слоев. Только нужна ли такая карта? Ведь карта в натуральную величину может быть с успехом заменена самой местностью ))))