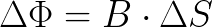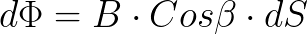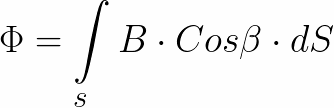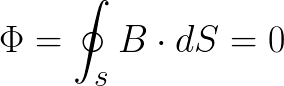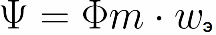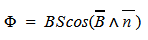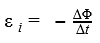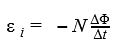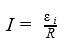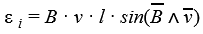Потокосцепление и магнитный поток

Из опыта известно, что возле постоянных магнитов, равно как и вблизи проводников с током, можно наблюдать физические эффекты, такие как механическое действие на другие магниты или проводники с током, а также появление ЭДС в движущихся в данном пространстве проводниках.

Необычное состояние пространства возле магнитов и проводников с током, называется магнитным полем, количественные характеристики которого легко определяются по данным явлениям: по силе механического воздействия или по электромагнитной индукции, по сути — по величине наводимой в движущемся проводнике ЭДС.

Явление наведения ЭДС в проводнике (явление электромагнитной индукции) проявляет себя в различных условиях. Вы можете двигать проводник через однородное магнитное поле, а можете просто изменять магнитное поле возле неподвижного проводника. В обоих случаях изменяющееся в пространстве магнитное поле станет наводить в проводнике ЭДС.

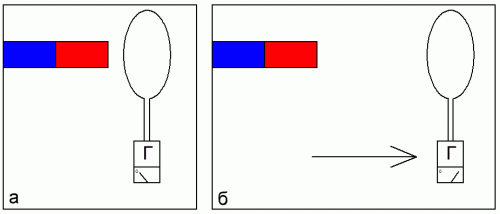
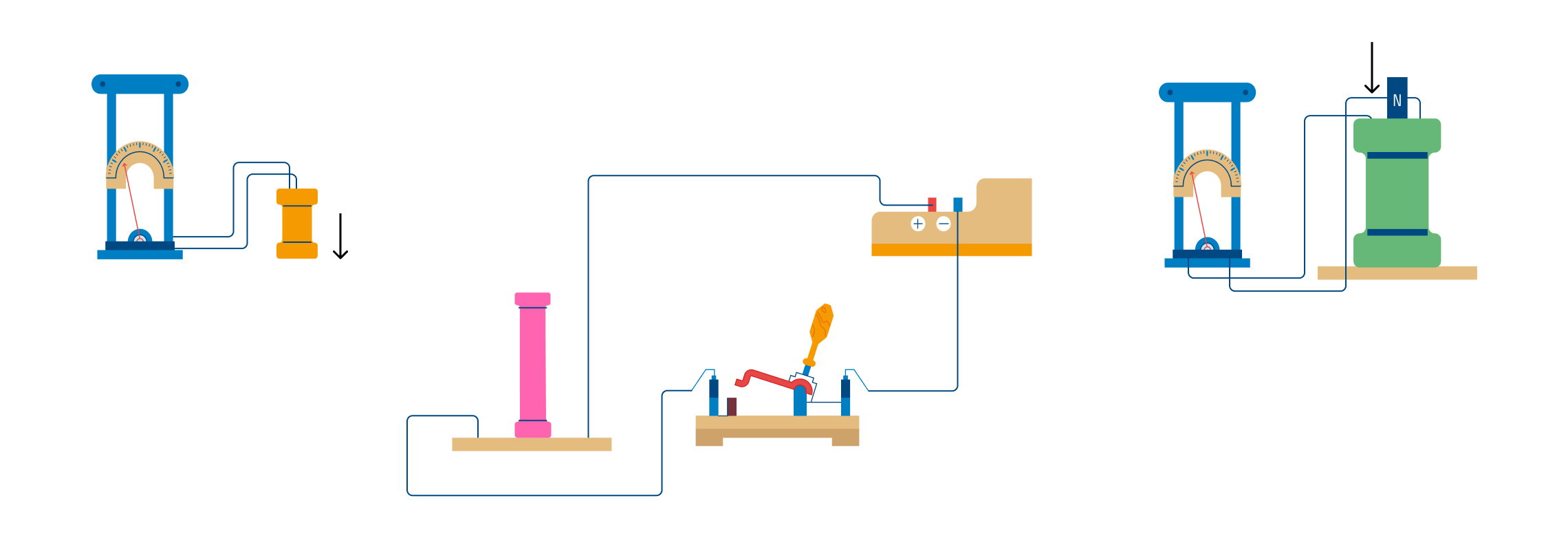
Простое экспериментальное приспособление для исследования данного явления изображено на рисунке. Здесь проводящее (медное) кольцо соединено своими выводами с баллистическим гальванометром, по отклонению стрелки которого можно будет судить о количестве электрического заряда, проходящего через эту нехитрую цепь. Сначала разместим кольцо центром в какой-нибудь точке пространства около магнита (положение а), затем резко отодвинем кольцо (в положение б). Гальванометр покажет значение прошедшего по цепи заряда Q.

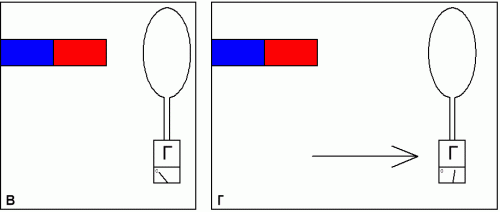
Теперь поместим кольцо в другую точку, чуть-чуть подальше от магнита (в положение в), и снова, с такой же скоростью, резко отодвинем его в сторону (в положение г). Отклонение стрелки гальванометра будут меньше чем в первом эксперименте. А если увеличить сопротивление петли R, например заменив медь на вольфрам, то перемещая кольцо аналогичным образом мы заметим, что гальванометр покажет заряд еще меньший, однако величина этого движущегося через гальванометр заряда в любом случае будет обратно пропорциональна сопротивлению петли.

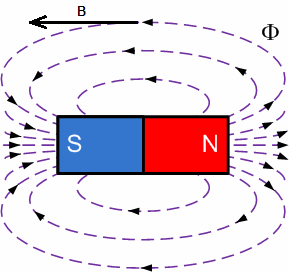
Эксперимент отчетливо демонстрирует, что пространство вокруг магнита в каждой его точке обладает каким-то свойством, чем-то таким, что напрямую влияет на количество заряда, проходящего через гальванометр, когда мы отодвигаем кольцо от магнита. Назовем это что-то, находящееся около магнита, магнитным потоком, и обозначим его количественную величину буквой Ф. Отметим выявленную зависимость Ф

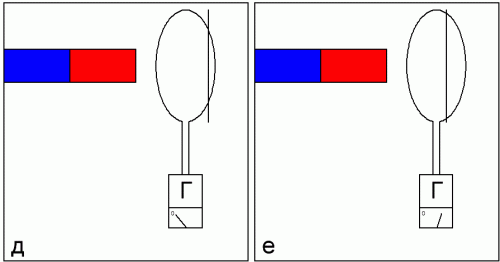
Усложним эксперимент. Закрепим медную петлю в определенной точке напротив магнита, рядом с ним (в положении д), но теперь будем изменять площадь петли (перекрывая ее часть проводником). Показания гальванометра будут пропорциональны изменению площади кольца (в положении е).

Следовательно действующий на петлю магнитный поток Ф от нашего магнита пропорционален площади петли. А вот магнитная индукция B, связанная с положением кольца относительно магнита, но не зависящая от параметров кольца, определяет свойство магнитного поля в каждой рассматриваемой точке пространства возле магнита.

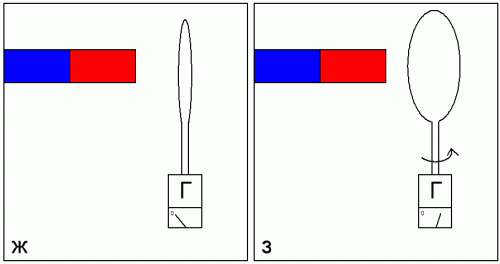
Продолжая эксперименты с медным кольцом, теперь будем изменять положение плоскости кольца относительно магнита в начальный момент (положение ж), и затем поворачивать его до положения вдоль оси магнита (положение з).

Заметим, что чем больше изменение угла между кольцом и магнитом — тем больше заряда Q протекает по цепи через гальванометр. Это значит, что магнитный поток через кольцо пропорционален косинусу угла между магнитом и нормалью к плоскости кольца.

Таким образом можно заключить, что магнитная индукция B – есть величина векторная, направление которой в данной точке совпадает с направлением нормали к плоскости кольца в том его положении, когда при резком отодвигании кольца далеко от магнита, проходящий по цепи заряд Q максимален.

Вместо магнита в эксперименте можно применять катушку электромагнита, отодвигать эту катушку или изменять в ней ток, усиливая или уменьшая таким образом магнитное поле, пронизывающее экспериментальный виток.

Площадь, пронизываемая магнитным полем, не обязательно может быть ограничена круглым витком, это может быть в принципе любая поверхность, магнитный поток через которую определяется тогда путем интегрирования:

Разделив пространство магнитного поля воображаемыми трубками единичного поперечного сечения S=1, можно получить так называемые единичные магнитные трубки, оси которых называют единичными магнитными линиями. При помощи данного подхода можно наглядно изобразить количественную картину магнитного поля, и в этом случае магнитный поток будет равен количеству линий, проходящих через выбранную поверхность.

Магнитные линии непрерывны, они выходят из северного полюса и обязательно входят в южный, поэтому суммарный магнитный поток через любую замкнутую поверхность равен нулю. Математически это выглядит так:

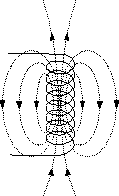
Рассмотрим магнитное поле, ограниченное поверхностью цилиндрической катушки. По сути — магнитный поток, пронизывающий поверхность, образованную витками данной катушки. В этом случае общую поверхность можно разделить на отдельные поверхности для каждого из витков катушки. На рисунке видно, что поверхности верхних и нижних витков катушки пронизываются четырьмя единичными магнитными линиями, а поверхности витков в середине катушки — восемью.

Чтобы найти величину полного магнитного потока через все витки катушки, необходимо суммировать магнитные потоки, пронизывающие поверхности каждого из ее витков, то есть магнитные потоки, сцепленные с отдельными витками катушки:

Ф = Ф1+Ф2+Ф3+Ф4+Ф5+Ф6+Ф7+Ф8, если в катушке 8 витков.

Для примера симметричной катушки, изображенной на предыдущем рисунке:

Ф верхних витков = 4+4+6+8 = 22;

Ф нижних витков = 4+4+6+8 = 22.

Ф общее = Ф верхних витков + Ф нижних витков = 44.

Здесь и вводится понятие «потокосцепление». Потокосцепление — это общий магнитный поток, сцепленный со всеми витками катушки, численно равный сумме магнитных потоков, сцепленных с отдельными ее витками:

Потокосцепление — величина виртуальная, так как реально нет никакой суммы отдельных магнитных потоков, а есть общий магнитный поток. Тем не менее, когда реальное распределение магнитного потока по виткам катушки неизвестно, а известно потокосцепление, то катушку можно заменить эквивалентной, вычислив количество эквивалентных одинаковых витков, необходимых для получения требуемого общего магнитного потока.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Потокосцепление

Потокосцепле́ние (полный магнитный поток) — физическая величина, представляющая собой суммарный магнитный поток, сцепляющийся со всеми витками катушки индуктивности.

Содержание

Определение

Потокосцепление численно равно сумме магнитных потоков, проходящих через каждый виток катушки, т.е. при количестве витков N и одинаковом магнитном потоке в каждом витке потокосцепление можно определить как где — магнитный поток одного витка [ Вб ].

В идеальном соленоиде все магнитные силовые линии проходят через каждый виток (т.е. не пересекают боковую поверхность соленоида), и, следовательно, магнитный поток каждого витка одинаков. Однако на практике магнитные потоки в витках катушки отличаются и величина потокосцепления определяется по формуле:

где:
— количество витков;
— номер витка, с которым сцеплен поток

В случае, если катушка имеет ферромагнитный сердечник, потокосцепление можно определить по формуле:

где — магнитный поток через магнитопровод (сердечник) катушки.

Величина потокосцепления, помимо магнитного потока, имеет связь с током I в индуктивности, определяющуюся выражением:

где — индуктивность катушки [ Гн ].

Эта формула выражает принцип непрерывности во времени потокосцепления катушки индуктивности.

Принцип непрерывности

Запас энергии магнитного поля в катушке индуктивности не может измениться скачком. Это выражает принцип непрерывности во времени. Невозможность скачкообразного изменения потокосцепления индуктивности объясняется, в свою очередь, тем, что в противном случае на индуктивности появилось бы бесконечно большое напряжение, что противоречит опыту.

Принцип непрерывности также означает, что ток в индуктивности не может измениться скачком (см. переходные процессы в электрических цепях):

— первый закон коммутации.

См. также

Литература

Полезное

Смотреть что такое «Потокосцепление» в других словарях:

потокосцепление — потокосцепление … Орфографический словарь-справочник

ПОТОКОСЦЕПЛЕНИЕ — полный магнитный поток, пронизывающий электрический контур. Напр., потокосцепление многовитковой катушки индуктивности равно сумме потоков через все ее витки. Единица измерения Вб … Большой Энциклопедический словарь

потокосцепление — сущ., кол во синонимов: 1 • поток (55) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

потокосцепление — Сумма магнитных потоков, сцепленных с элементами контура электрической цепи. [ГОСТ Р 52002 2003] Тематики электротехника, основные понятия … Справочник технического переводчика

потокосцепление — 113 потокосцепление Сумма магнитных потоков, сцепленных с элементами контура электрической цепи 114 потокосцепление самоиндукции Потокосцепление элемента электрической цепи, обусловленное электрическим током в этом элементе 115 (собственная)… … Словарь-справочник терминов нормативно-технической документации

потокосцепление — полный магнитный поток, пронизывающий электрический контур. Например, потокосцепление многовитковой катушки индуктивности равно сумме потоков через все её витки. Единица измерения вебер (Вб). * * * ПОТОКОСЦЕПЛЕНИЕ ПОТОКОСЦЕПЛЕНИЕ, полный… … Энциклопедический словарь

Потокосцепление — в электротехнике, полный магнитный поток (ψ), сцепленный с рассматриваемым контуром. По существу П. всегда совпадает с потоком в интегральном определении: Φ = = ψ, где В вектор магнитной индукции, рис.); при этом общий поток, или П., ω… … Большая советская энциклопедия

потокосцепление — visuminė magnetovara statusas T sritis Standartizacija ir metrologija apibrėžtis Visuminis elektrinio laidumo srovės, tekančios uždaruoju kontūru, stipris. atitikmenys: angl. current linkage vok. Flussverkettung, f rus. потокосцепление, n pranc.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

потокосцепление — visuminė magnetovara statusas T sritis fizika atitikmenys: angl. current linkage vok. Flussverkettung, f rus. потокосцепление, n pranc. flux embrassé, m; flux magnétique embrassé, m … Fizikos terminų žodynas

Источник

Магнитный поток и потокосцепление

В пространстве, окружающем проводники, по которым протекает электрический ток, а также окружающем постоянные магниты, существует ряд физических явлений, проявляющихся в возникновении ЭДС в движущихся проводниках, механическом воздействии на постоянные магниты и проводники с током, находящиеся в этом пространстве и др.

Для определения количественных характеристик магнитного поля можно использовать любое его проявление, однако обычно используют явление электромагнитной индукции и механическое воздействие со стороны поля.

Если опыты в точке a продолжить, изменяя положение плоскости кольца в начальный момент, то можно установить, что существует такое его положение, при котором количество зарядов будет максимальным и всякое отклонение от этого положения будет приводить к их уменьшению пропорционально косинусу угла отклонения. Включая это условие в выражение (2) получим

Выражение (3) показывает, что магнитная индукция B является векторной величиной и ее направление совпадает с направлением нормали к плоскости пробного витка, при котором количество зарядов, протекающих через виток при его удалении на значительное расстояние, максимально.

Опыты с пробным витком (кольцом) можно проводить также и в пространстве катушки, подключенной к источнику постоянного тока. При этом вместо удаления витка можно просто выключать ток, т.к. в обоих случаях магнитный поток будет уменьшаться до нуля.

Из выражения (4) следует, что:

В описанных выше опытах с пробным витком (кольцом), он удалялся на такое расстояние, при котором исчезали всякие проявления магнитного поля. Но можно просто перемещать этот виток в пределах поля и при этом в нем также будут перемещаться электрические заряды. Перейдем в выражении (1) к приращениям

С помощью пробного витка можно исследовать все пространство вокруг магнита или катушки с током и построить линии, направление касательных к которым в каждой точке будет соответствовать направлению вектора магнитной индукции B (рис. 3)

Магнитные линии непрерывны и этот принцип можно математически представить в виде

Для того, чтобы определить полный магнитный поток, проходящий через поверхность всех витков, нужно сложить потоки, проходящие через поверхности отдельных витков, или, иначе говоря, сцепляющиеся с отдельными витками. Например, магнитные потоки, сцепляющиеся с четырьмя верхними витками катушки рис. 4, будут равны: Ф 1 =4; Ф 2 =4; Ф 3 =6; Ф 4 =8. Также, зеркально-симметрично с нижними.

То есть для приведенного на рисунке случая, двух зеркально-симметричных половинок катушки:

Ψ = 2(Ф 1 + Ф 2 + Ф 3 + Ф 4 ) = 48

Источник

Закон электромагнитной индукции

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Магнитный поток

Прежде, чем разобраться с тем, что такое электромагнитная индукция, нужно определить такую сущность, как магнитный поток.

Представьте, что вы взяли обруч в руки и вышли на улицу в ливень. Чем сильнее ливень, тем больше через этот обруч пройдет воды — поток воды больше.

Если обруч расположен горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.

Теперь давайте поставим обруч вертикально — ни одной капли не пройдет сквозь него (если ветер не подует, конечно).

Магнитный поток по сути своей — это тот же самый поток воды через обруч, только считаем мы величину прошедшего через площадь магнитного поля, а не дождя.

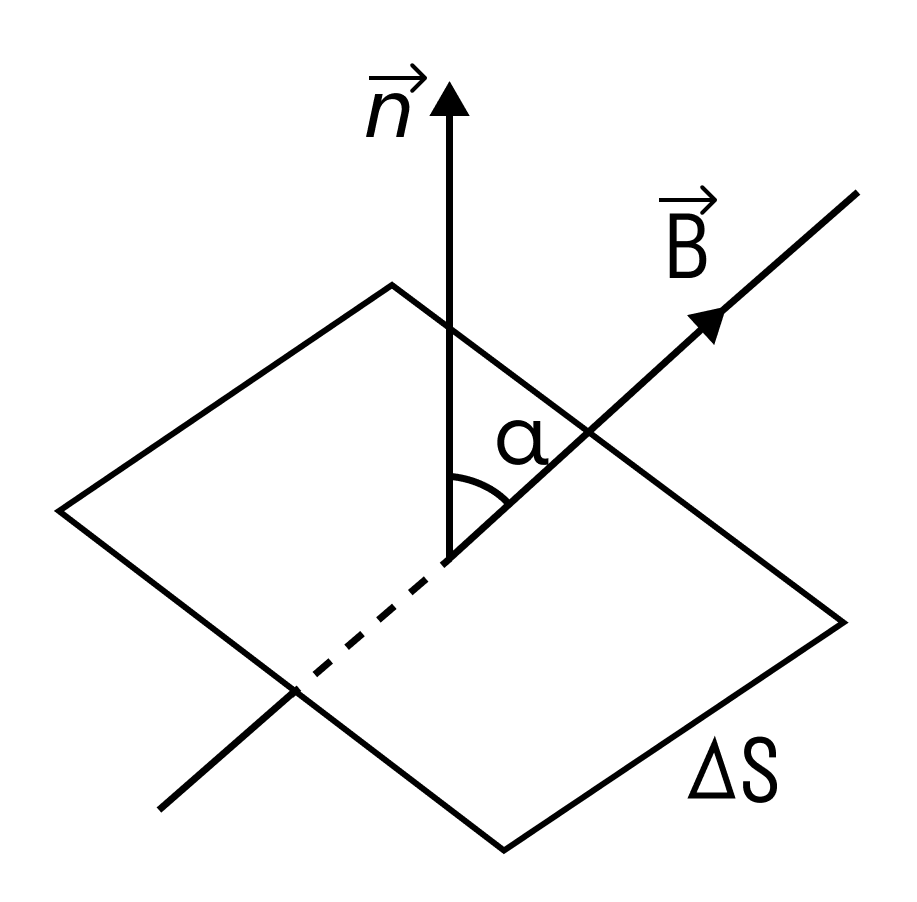
Магнитным потоком через площадь ​S​ контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ​B​, площади поверхности ​S​, пронизываемой данным потоком, и косинуса угла ​α​ между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):

Магнитный поток

Ф — магнитный поток [Вб]

B — магнитная индукция [Тл]

S — площадь пронизываемой поверхности [м^2]

n — вектор нормали (перпендикуляр к поверхности) [-]

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла ​α магнитный поток может быть положительным (α 90°). Если α = 90°, то магнитный поток равен 0. Это зависит от величины косинуса угла.

Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура, магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Электромагнитная индукция

Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было открыто М. Фарадеем.

Майкл Фарадей провел ряд опытов, которые помогли открыть явление электромагнитной индукции.

Опыт раз. На одну непроводящую основу намотали две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.

При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.

Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.

Опыт три. Катушка замкнута на гальванометр, а магнит движется вдвигается (выдвигается) относительно катушки

Вот, что показали эти опыты:

Почему возникает индукционный ток?

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС.

Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Закон электромагнитной индукции

Закон электромагнитной индукции (закон Фарадея) звучит так:

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.

Математически его можно описать формулой:

Закон Фарадея

Ɛi — ЭДС индукции [В]

ΔФ/Δt — скорость изменения магнитного потока [Вб/с]

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из ​N витков (то есть он — катушка), то ЭДС индукции будет вычисляться следующим образом.

Закон Фарадея для контура из N витков

Ɛi — ЭДС индукции [В]

ΔФ/Δt — скорость изменения магнитного потока [Вб/с]

N — количество витков [-]

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ​R​:

Закон Ома для проводящего контура

Ɛi — ЭДС индукции [В]

I — сила индукционного тока [А]

R — сопротивление контура [Ом]

Если проводник длиной l будет двигаться со скоростью ​v​ в постоянном однородном магнитном поле с индукцией ​B​ ЭДС электромагнитной индукции равна:

ЭДС индукции для движущегося проводника

Ɛi — ЭДС индукции [В]

B — магнитная индукция [Тл]

v — скорость проводника [м/с]

l — длина проводника [м]

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

Правило Ленца

Чтобы определить направление индукционного тока, нужно воспользоваться правилом Ленца.

Академически это правило звучит следующим образом: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

Давайте попробуем чуть проще: катушка в данном случае — это недовольная бабуля. Забирают у нее магнитный поток — она недовольна и создает магнитное поле, которое этот магнитный поток хочет обратно отобрать.

Дают ей магнитный поток, забирай, мол, пользуйся, а она такая — «Да зачем сдался мне ваш магнитный поток!» и создает магнитное поле, которое этот магнитный поток выгоняет.

Источник

• визитки установка дверей шаблоны →