Что называется круговым процессом циклом
Физика Б1.Б8.
Молекулярная физика и термодинамика
1. Введение
Основы молекулярной физики были заложены трудами Ломоносова, Джоуля, Больцмана, Клаузиуса, Максвелла и других ученых. Благодаря их трудам молекулярная физика прочно утвердилась в науке. Непосредственным опытным подтверждением молекулярно-кинетической теории являются процесс диффузии, броуновского движения, распространения запаха и многие другие явления.
Движение каждой молекулы в веществе может быть описано законами классической механики. Однако число молекул в веществе чрезвычайно велико, направления и величины скоростей молекул совершенно случайны и непрерывно изменяются так, что становится невозможным охватить уравнениями движения всю совокупность молекул и сделать какие-либо выводы об их поведении.
Тем не менее, состояние вещества и его изменение определяется заданием небольшого числа определенных параметров, как температура, давление, объем, плотность и т.д., значения которых невозможно указать на основе решений уравнений классической механики. Дело в том, что свойства огромного числа молекул подчиняется особым, статистическим закономерностям. Статистическая физика изучает статистические закономерности, описывающие поведение большой совокупности объектов. Она основывается на теории вероятностей и позволяет вычислять средние значения величин, характеризующих движение всей совокупности молекул (средние скорости молекул, средние кинетические энергии, средние значения импульса и т. д.) и на этой основе истолковывает свойства вещества, непосредственно наблюдаемые на опыте (давление, температура и т.д.). В этом состоит суть молекулярно-кинетического изучения вещества.
Наряду со статистическим, существует термодинамический метод изучения вещества. В отличие от статистического метода термодинамический метод не интересуется строением вещества. Термодинамика изучают условия превращения энергии и характеризует их с количественной стороны.
В основе термодинамики лежит небольшое число закономерностей, установленных на основе большого числа опытных фактов и получивших название начала термодинамики.
У статистической физики и термодинамики общий предмет изучения – свойства вещества и происходящие в нем процессы. Подходя к изучению этих свойств с разных точек зрения, эти методы взаимно дополняют друг друга.
Совокупность тел, могущих обмениваться энергией между собой и с внешними телами, не входящими в эту систему, называется термодинамической системой. Одним из основных понятий термодинамики является понятие состояния системы. Состояние системы определяется совокупностью значений всех величин, характеризующих физические свойства системы и называемых термодинамическими параметрами (температура, давление плотность, теплоемкость, электропроводность и т. д.). Состояние системы называется стационарным, если значения всех термодинамических параметров не изменяются во времени. Стационарное состояние называется равновесным, если его неизменность не обусловлена протеканием каких-либо процессов во внешних по отношению к данной системе телах.
Исследования показывают, что параметры состояния тел взаимно связаны и могут быть выражены друг через друга. Поэтому термодинамическое состояние задается только ограниченным числом параметров состояния. Такие параметры называются основными параметрами состояния. Важнейшими параметрами состояния химически однородных систем являются плотность, объем, давление, температура. И между этими параметрами существует связь, выражаемая в виде математического уравнения 
Что называется круговым процессом циклом
2.3.1. Обратимые и круговые процессы
Обратимым процессом называется такой процесс, который может быть проведен в обратном направлении таким образом, что система будет проходить через те же термодинамические состояния, что и при прямом процессе, но в обратной последовательности. Обратимым может быть только равновесный процесс.
Обратимый процесс обладает следующим свойством: если при прямом ходе на каком-то элементарном участке система получает тепло dQ и совершает работу dA, то при обратном ходе на том же участке система отдает тепло dQ’ = dQ и над ней совершается работа dA’ = dA. По этой причине после протекания обратимого процесса в одном, а затем в обратном направлении и возвращения системы в первоначальное состояние в окружающих систему телах не должно произойти никаких изменений.
Круговым процессом (циклом) называется такой процесс, при котором система после ряда изменений возвращается в исходное состояние. На графике цикл изображается замкнутой кривой (Рис. 2.3.1).
Рис. 2.3.1. Круговой термодинамический процесс
Работа, совершаемая при круговом процессе, численно равна площади, охватываемой кривой. Действительно, работа на участке 1-2 положительна и численно равна площади, отмеченной наклоненной вправо штриховкой. Работа на участке 2-1 отрицательна и численно равна площади, отмеченной наклоненной влево штриховкой. Следовательно, работа за цикл численно равна площади, охватываемой кривой.
После совершения цикла система возвращается в исходное состояние.
2.3.2. Коэффициент полезного
действия тепловой машины
Всякий двигатель представляет собой систему, совершающую многократно некоторый круговой процесс (цикл). Пусть в ходе цикла рабочее вещество (например, газ) сначала расширяется до объема V2, а затем снова сжимается до первоначального объема V1(Рис. 2.3.2).
Рис. 2.3.2. К расчету кпд тепловой машины
Чтобы работа за цикл была больше нуля, давление (а, следовательно, и температура) в процессе расширения должно быть больше, чем при сжатии. Для этого рабочему веществу нужно в ходе расширения сообщать, а в ходе сжатия отнимать от него тепло.
Напишем первое начало термодинамики для обеих частей цикла. При расширении внутренняя энергия изменяется от значения U1 до U2, при этом система получает тепло Q1 и совершает работу А1. Поэтому выполняется:
При сжатии система совершает работу А2 и отдает тепло Q2, что равносильно получению тепла Q2. Следовательно,
Складывая уравнения (2.3.1) и (2.3.2), получаем:
Поскольку А1 + А2 есть полная работа А, совершаемая системой за цикл, можно записать:
Как следует из (2.3.4), не все получаемое извне тепло Q1 используется для получения полезной работы. Для того, чтобы двигатель работал циклами, часть тепла Q2 должна быть возвращена во внешнюю среду и, следовательно, не используется по назначению. Очевидно, что чем полнее тепловая машина превращает получаемое извне тепло Q1 в полезную работу А, тем эта машина выгоднее. Поэтому тепловую машину принято характеризовать коэффициентом полезного действия (КПД), который определяется как отношение совершаемой за цикл работы к получаемому за цикл количеству тепла Q1:
Из определения КПД следует, что он не может быть больше единицы.
2.3.3. Второе начало термодинамики
Второе начало термодинамики, как и первое, может быть сформулировано несколькими способами. В наиболее очевидной формулировке второе начало гласит, что:
невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому. Более строго, невозможны такие процессы, единственным конечным результатом которых был бы переход тепла от тела, менее нагретого, к телу, более нагретому.
Еще одна формулировка: невозможны такие процессы, единственным конечным результатом которых явилось бы отнятие от некоторого тела определенного количества тепла и превращение этого тепла в работу полностью.
Работа может быть полностью превращена в тепло, например, посредством трения, обратное неверно.
2.3.4. Цикл Карно
Предположим, что какое-либо тело может вступать в теплообмен с двумя тепловыми резервуарами, имеющими температуры Т1 и Т2 и обладающими бесконечно большой теплоемкостью. Это означает, что получение или отдача этими резервуарами конечного количества тепла не изменяет их температуры. Выясним, какой обратимый цикл может совершать тело в таких условиях.
Рассматриваемый цикл может состоять как из процессов, в ходе которых тело обменивается теплом с резервуарами, так и из процессов, не сопровождающихся теплообменом с окружающей средой, т.е. происходящих адиабатически.
Рассмотрим, как может быть осуществлен цикл Карно с газом в качестве рабочего вещества. Поместим газ в цилиндр, закрытый плотно пригнанным поршнем. Пусть стенки и поршень сделаны из непроводящих тепло материалов, дно цилиндра, напротив, изготовлено из материала с высокой теплопроводностью. Теплоемкость цилиндра и поршня считается бесконечно малой.
Пусть первоначально поршень занимает положение, отвечающее объему V1 и температуре газа Т1. Поставим цилиндр на резервуар, имеющий температуру Т1, и предоставим газу возможность очень медленно расширяться до объема V2. При этом газ получит от резервуара тепло Q1 (Рис. 2.3.3).
Рис. 2.3.3. Тепловая машина, работающая по циклу Карно
Затем снимем цилиндр с резервуара, закроем дно теплоизолирующей крышкой и позволим газу расширяться адиабатически до тех пор, пока его температура не упадет до значения Т2. Объем газа в результате станет равным V3. Убрав теплоизолирующую крышку, поставим цилиндр на резервуар, имеющий температуру Т2 и сожмем газ изотермически до такого объема V4, чтобы при последующем адиабатическом сжатии при достижении температуры Т1 объем получил значение V1 (иначе цикл не замкнется). Наконец, снимем цилиндр с резервуара, закроем дно теплоизолирующей крышкой и, сжимая газ адиабатически, приведем его в первоначальное состояние (температура Т1, объем V1).
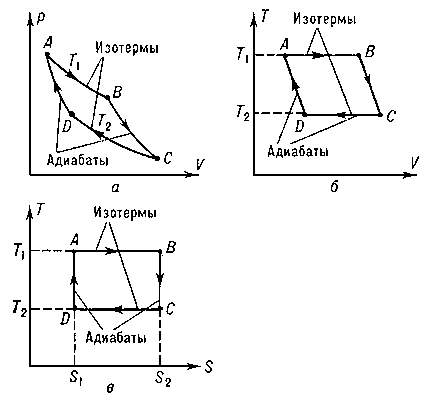
Если газ идеальный, соответствующий цикл на (р-V) диаграмме имеет вид, показанный на Рис. 2.3.4.
Рис. 2.3.4. (р-V) диаграмма цикла Карно
2.3.5. КПД цикла Карно для идеального газа
Рассмотрим цикл Карно для идеального газа. КПД тепловой машины равен:
При изотермическом процессе внутренняя энергия идеального газа остается постоянной. Поэтому количество полученного газом тепла Q1 равно работе А12, совершаемой газом при переходе из состояния 1 в состояние 2 (Рис. 2.3.4). Эту работу можно рассчитать так:
Используя уравнение Клапейрона-Менделеева, получим:
Количество отдаваемого холодильнику тепла Q2 равно работе А34, затрачиваемой на сжатие газа при переводе его из состояния 3 в состояние 4. Эта работа равна:
Для того, чтобы цикл был замкнутым, нужно, чтобы состояния 4 и 1 лежали на одной и той же адиабате. Отсюда с помощью (2.1.68) можно получить:
Аналогично, поскольку состояния 2 и 3 лежат на одной и той же адиабате, выполняется:
Деля (2.3.11) на (2.3.10), приходим к условию замкнутости цикла:
Подставляя (2.3.8) и (2.3.9) в (2.3.6), имеем:
Окончательно, учитывая условие (2.3.12), для КПД тепловой машины, работающей по циклу Карно для идеального газа, получаем:
Следовательно, КПД цикла Карно для идеального газа оказывается зависящим только от температуры нагревателя и холодильника.
Даже для наилучшей тепловой машины, работающей по циклу Карно, КПД всегда значительно меньше единицы. Если, например, температура нагревателя Т1 = 373К (температура кипения воды), а температура холодильника Т2 = 293К (комнатная температура), то η = 22%. И этот КПД является верхним (и недостижимым) пределом. В реальных машинах, например, на паровозах, редко превосходил 10%.
2.3.6. Энтропия
Обратим внимание на те изменения, которые претерпело рабочее тело в процессе кругового цикла Карно. Из исходного состояния 1 (давление р1, температура Т1) рабочее тело путем последовательного проведения изотермического и адиабатического расширений перешло в состояние 3, когда оно приняло температуру холодильника Т2. Это изменение состояния произошло за счет тепла Q1, доставленного рабочему телу нагревателем. Обратный переход рабочего тела из состояния 3 в исходное состояние 1 был осуществлен двумя последовательно проведенными изотермическим и адиабатическим сжатиями тела. Выделившееся при этом возвращении в исходное состояние количество тепла равно Q2, причем Q2
Обобщим данный результат. Любое изменение состояния тела или системы тел в общем случае можно представить как результат бесконечно большого числа бесконечно малых изменений. При каждом таком бесконечно малом изменении система либо поглощает, либо выделяет бесконечно малое количество тепла dQ (если процесс не адиабатический). Пусть dQ > 0, когда система поглощает тепло.
Можно показать, что если система в результате каких-либо изменений состояния переходит обратимым путем из состояния А в состояние В, то сумма приведенных количеств теплоты не зависит от пути, по которому происходил этот переход. Это означает, что интеграл по замкнутому контуру должен быть равен нулю:
Отсюда следует, что для обратимого процесса интеграл не зависит от пути, по которому проходит процесс, и зависит только от начального и конечного положений. Поэтому вводят новую величину, которая называется энтропией :
Тогда первое начало термодинамики можно записать так:
Энтропия изолированной системы может только возрастать (если в системе протекает необратимый процесс), или оставаться постоянной в случае обратимого процесса.
Нернстом доказана теорема (иногда называемая третьим началом термодинамики), согласно которой при стремлении абсолютной температуры к нулю энтропия любого тела также стремится к нулю:
Тогда энтропию состояния тела при температуре Т можно вычислить так:
© ФГОУ ВПО Красноярский государственный аграрный университет, 2015
Что называется круговым процессом циклом
2.3.1. Обратимые и круговые процессы
Обратимым процессом называется такой процесс, который может быть проведен в обратном направлении таким образом, что система будет проходить через те же термодинамические состояния, что и при прямом процессе, но в обратной последовательности. Обратимым может быть только равновесный процесс.
Обратимый процесс обладает следующим свойством: если при прямом ходе на каком-то элементарном участке система получает тепло dQ и совершает работу dA, то при обратном ходе на том же участке система отдает тепло dQ’ = dQ и над ней совершается работа dA’ = dA. По этой причине после протекания обратимого процесса в одном, а затем в обратном направлении и возвращения системы в первоначальное состояние в окружающих систему телах не должно произойти никаких изменений.
Круговым процессом (циклом) называется такой процесс, при котором система после ряда изменений возвращается в исходное состояние. На графике цикл изображается замкнутой кривой (Рис. 2.3.1).
Рис. 2.3.1. Круговой термодинамический процесс
Работа, совершаемая при круговом процессе, численно равна площади, охватываемой кривой. Действительно, работа на участке 1-2 положительна и численно равна площади, отмеченной наклоненной вправо штриховкой. Работа на участке 2-1 отрицательна и численно равна площади, отмеченной наклоненной влево штриховкой. Следовательно, работа за цикл численно равна площади, охватываемой кривой.
После совершения цикла система возвращается в исходное состояние.
2.3.2. Коэффициент полезного
действия тепловой машины
Всякий двигатель представляет собой систему, совершающую многократно некоторый круговой процесс (цикл). Пусть в ходе цикла рабочее вещество (например, газ) сначала расширяется до объема V2, а затем снова сжимается до первоначального объема V1(Рис. 2.3.2).
Рис. 2.3.2. К расчету кпд тепловой машины
Чтобы работа за цикл была больше нуля, давление (а, следовательно, и температура) в процессе расширения должно быть больше, чем при сжатии. Для этого рабочему веществу нужно в ходе расширения сообщать, а в ходе сжатия отнимать от него тепло.
Напишем первое начало термодинамики для обеих частей цикла. При расширении внутренняя энергия изменяется от значения U1 до U2, при этом система получает тепло Q1 и совершает работу А1. Поэтому выполняется:
При сжатии система совершает работу А2 и отдает тепло Q2, что равносильно получению тепла Q2. Следовательно,
Складывая уравнения (2.3.1) и (2.3.2), получаем:
Поскольку А1 + А2 есть полная работа А, совершаемая системой за цикл, можно записать:
Как следует из (2.3.4), не все получаемое извне тепло Q1 используется для получения полезной работы. Для того, чтобы двигатель работал циклами, часть тепла Q2 должна быть возвращена во внешнюю среду и, следовательно, не используется по назначению. Очевидно, что чем полнее тепловая машина превращает получаемое извне тепло Q1 в полезную работу А, тем эта машина выгоднее. Поэтому тепловую машину принято характеризовать коэффициентом полезного действия (КПД), который определяется как отношение совершаемой за цикл работы к получаемому за цикл количеству тепла Q1:
Из определения КПД следует, что он не может быть больше единицы.
2.3.3. Второе начало термодинамики
Второе начало термодинамики, как и первое, может быть сформулировано несколькими способами. В наиболее очевидной формулировке второе начало гласит, что:
невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому. Более строго, невозможны такие процессы, единственным конечным результатом которых был бы переход тепла от тела, менее нагретого, к телу, более нагретому.
Еще одна формулировка: невозможны такие процессы, единственным конечным результатом которых явилось бы отнятие от некоторого тела определенного количества тепла и превращение этого тепла в работу полностью.
Работа может быть полностью превращена в тепло, например, посредством трения, обратное неверно.
2.3.4. Цикл Карно
Предположим, что какое-либо тело может вступать в теплообмен с двумя тепловыми резервуарами, имеющими температуры Т1 и Т2 и обладающими бесконечно большой теплоемкостью. Это означает, что получение или отдача этими резервуарами конечного количества тепла не изменяет их температуры. Выясним, какой обратимый цикл может совершать тело в таких условиях.
Рассматриваемый цикл может состоять как из процессов, в ходе которых тело обменивается теплом с резервуарами, так и из процессов, не сопровождающихся теплообменом с окружающей средой, т.е. происходящих адиабатически.
Рассмотрим, как может быть осуществлен цикл Карно с газом в качестве рабочего вещества. Поместим газ в цилиндр, закрытый плотно пригнанным поршнем. Пусть стенки и поршень сделаны из непроводящих тепло материалов, дно цилиндра, напротив, изготовлено из материала с высокой теплопроводностью. Теплоемкость цилиндра и поршня считается бесконечно малой.
Пусть первоначально поршень занимает положение, отвечающее объему V1 и температуре газа Т1. Поставим цилиндр на резервуар, имеющий температуру Т1, и предоставим газу возможность очень медленно расширяться до объема V2. При этом газ получит от резервуара тепло Q1 (Рис. 2.3.3).
Рис. 2.3.3. Тепловая машина, работающая по циклу Карно
Затем снимем цилиндр с резервуара, закроем дно теплоизолирующей крышкой и позволим газу расширяться адиабатически до тех пор, пока его температура не упадет до значения Т2. Объем газа в результате станет равным V3. Убрав теплоизолирующую крышку, поставим цилиндр на резервуар, имеющий температуру Т2 и сожмем газ изотермически до такого объема V4, чтобы при последующем адиабатическом сжатии при достижении температуры Т1 объем получил значение V1 (иначе цикл не замкнется). Наконец, снимем цилиндр с резервуара, закроем дно теплоизолирующей крышкой и, сжимая газ адиабатически, приведем его в первоначальное состояние (температура Т1, объем V1).
Если газ идеальный, соответствующий цикл на (р-V) диаграмме имеет вид, показанный на Рис. 2.3.4.
Рис. 2.3.4. (р-V) диаграмма цикла Карно
2.3.5. КПД цикла Карно для идеального газа
Рассмотрим цикл Карно для идеального газа. КПД тепловой машины равен:
При изотермическом процессе внутренняя энергия идеального газа остается постоянной. Поэтому количество полученного газом тепла Q1 равно работе А12, совершаемой газом при переходе из состояния 1 в состояние 2 (Рис. 2.3.4). Эту работу можно рассчитать так:
Используя уравнение Клапейрона-Менделеева, получим:
Количество отдаваемого холодильнику тепла Q2 равно работе А34, затрачиваемой на сжатие газа при переводе его из состояния 3 в состояние 4. Эта работа равна:
Для того, чтобы цикл был замкнутым, нужно, чтобы состояния 4 и 1 лежали на одной и той же адиабате. Отсюда с помощью (2.1.68) можно получить:
Аналогично, поскольку состояния 2 и 3 лежат на одной и той же адиабате, выполняется:
Деля (2.3.11) на (2.3.10), приходим к условию замкнутости цикла:
Подставляя (2.3.8) и (2.3.9) в (2.3.6), имеем:
Окончательно, учитывая условие (2.3.12), для КПД тепловой машины, работающей по циклу Карно для идеального газа, получаем:
Следовательно, КПД цикла Карно для идеального газа оказывается зависящим только от температуры нагревателя и холодильника.
Даже для наилучшей тепловой машины, работающей по циклу Карно, КПД всегда значительно меньше единицы. Если, например, температура нагревателя Т1 = 373К (температура кипения воды), а температура холодильника Т2 = 293К (комнатная температура), то η = 22%. И этот КПД является верхним (и недостижимым) пределом. В реальных машинах, например, на паровозах, редко превосходил 10%.
2.3.6. Энтропия
Обратим внимание на те изменения, которые претерпело рабочее тело в процессе кругового цикла Карно. Из исходного состояния 1 (давление р1, температура Т1) рабочее тело путем последовательного проведения изотермического и адиабатического расширений перешло в состояние 3, когда оно приняло температуру холодильника Т2. Это изменение состояния произошло за счет тепла Q1, доставленного рабочему телу нагревателем. Обратный переход рабочего тела из состояния 3 в исходное состояние 1 был осуществлен двумя последовательно проведенными изотермическим и адиабатическим сжатиями тела. Выделившееся при этом возвращении в исходное состояние количество тепла равно Q2, причем Q2
Обобщим данный результат. Любое изменение состояния тела или системы тел в общем случае можно представить как результат бесконечно большого числа бесконечно малых изменений. При каждом таком бесконечно малом изменении система либо поглощает, либо выделяет бесконечно малое количество тепла dQ (если процесс не адиабатический). Пусть dQ > 0, когда система поглощает тепло.
Можно показать, что если система в результате каких-либо изменений состояния переходит обратимым путем из состояния А в состояние В, то сумма приведенных количеств теплоты не зависит от пути, по которому происходил этот переход. Это означает, что интеграл по замкнутому контуру должен быть равен нулю:
Отсюда следует, что для обратимого процесса интеграл не зависит от пути, по которому проходит процесс, и зависит только от начального и конечного положений. Поэтому вводят новую величину, которая называется энтропией :
Тогда первое начало термодинамики можно записать так:
Энтропия изолированной системы может только возрастать (если в системе протекает необратимый процесс), или оставаться постоянной в случае обратимого процесса.
Нернстом доказана теорема (иногда называемая третьим началом термодинамики), согласно которой при стремлении абсолютной температуры к нулю энтропия любого тела также стремится к нулю:
Тогда энтропию состояния тела при температуре Т можно вычислить так:
© ФГОУ ВПО Красноярский государственный аграрный университет, 2015
Круговой процесс
Полезное
Смотреть что такое «Круговой процесс» в других словарях:
КРУГОВОЙ ПРОЦЕСС — (цикл), термодинамич. процесс, при к ром система, претерпев ряд изменений, возвращается в исходное состояние. Термодинамич. параметры и характеристические функции состояния системы (внутренняя энергия U, энтальпия, изохорный и изобарный… … Физическая энциклопедия
КРУГОВОЙ ПРОЦЕСС — (цикл термодинамический) термодинамич. процесс, при к ром все термодинамич. параметры (и термодинамич. ф ции) возвращаются к своим нач. значениям. Если термодинамич. состояние определяется двумя параметрами (напр., давлением Р и объёмом V), К. п … Физическая энциклопедия
КРУГОВОЙ ПРОЦЕСС — КРУГОВОЙ ПРОЦЕСС, то же, что цикл термодинамический … Современная энциклопедия
КРУГОВОЙ ПРОЦЕСС — совокупность термодинамических процессов, в результате которых рабочее тело (напр., пар в тепловой машине), пройдя через ряд промежуточных состояний, возвращается в исходное состояние … Большой Энциклопедический словарь
Круговой процесс — КРУГОВОЙ ПРОЦЕСС, то же, что цикл термодинамический. … Иллюстрированный энциклопедический словарь
круговой процесс — uždarasis vyksmas statusas T sritis Standartizacija ir metrologija apibrėžtis Termodinaminės sistemos būsenos kitimas, kuriam pasibaigus sistema grįžta į pradinę būseną. atitikmenys: angl. cyclic process vok. Kreislauf, m; Kreisprozess, m rus.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
круговой процесс — uždarasis procesas statusas T sritis chemija apibrėžtis Termodinaminės sistemos būsenos kitimas, kuriam pasibaigus sistema grįžta į pradinę būseną. atitikmenys: angl. cyclic process rus. замкнутый процесс; круговой процесс ryšiai: sinonimas –… … Chemijos terminų aiškinamasis žodynas
круговой процесс — ciklinis vyksmas statusas T sritis fizika atitikmenys: angl. cyclic process vok. Kreislauf, m; Kreisprozeß, m; zyklischer Prozeß, m rus. круговой процесс, m; циклический процесс, m pranc. processus cyclique, m … Fizikos terminų žodynas
круговой процесс — совокупность термодинамических процессов, в результате которых рабочее тело (например, пар в тепловой машине), пройдя через ряд промежуточных состояний, возвращается в исходное состояние. * * * КРУГОВОЙ ПРОЦЕСС КРУГОВОЙ ПРОЦЕСС, совокупность… … Энциклопедический словарь
круговой процесс — ciklas statusas T sritis Energetika apibrėžtis Reiškinių, procesų, sudarančių užbaigtą raidos ratą, visuma. atitikmenys: angl. cycle vok. Kreislauf, m rus. круговой процесс, m; цикл, m pranc. cycle, m … Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas