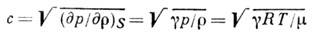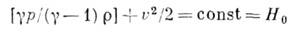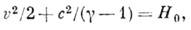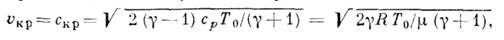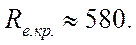Что называется критической скоростью гидравлика

Что такое критическая скорость? Что она определяет?

КРИТИЧЕСКАЯ СКОРОСТЬ—скорость, при которой ламинарное течение жидкости переходит в турбулентное. К. с. прямо пропорциональна коэффициенту кинематической вязкости и числу Рейнольдса и обратно пропорциональна гидравлическому радиусу. КРИТИЧЕСКАЯ СКОРОСТЬ в гидроаэродинамике, скорость, при которой качественно меняются картина течения жидкости (или газа) и его основной характеристики. Существование критической скорости обусловлено сложной природой течений, свойства которых зависят от распределения сил и термодинамических потенциалов, а также от состава и геометрии среды.

Величина критической скорости определяет закономерности затопления местности при разрушении плотин или накате цунами на берег.

19. Что такое сопротивление движения по длине?

Что является критерием для определения движения жидкости?

Критерием режима движения жидкости является безразмерная величина, которая впоследствии была названа числом Рейнольдса Re.

В общем случае число Рейнольдса Re определяется по формуле

, где V– средняя скорость потока;D_г– гидравлический диаметр сечения,D_г= 4R_г;n– кинематический коэффициент вязкости.

21. Указать критическое значение числа Re для напорного движения. Что оно определяет?

Для напорного движения в цилиндрических трубах удобнее число Рейнольдса определять по отношению к диаметру d, т. е.

, (82′) где d – диаметр трубы.

В этом случае R_eKp получается равным

2300. Если в формуле (82′) для трубопроводов круглого сечения d выразить черезгидравлический радиус ,то получим R_eKp=575.

Число Рейнольдса как критерий перехода от ламинарного к турбулентному режиму течения и обратно относительно хорошо действует для напорных потоков. При переходе к безнапорным потокам переходная зона между ламинарным и турбулентным режимами возрастает, и использование числа Рейнольдса как критерия не всегда правомерно.

Какими способами можно определить режим движения жидкости?

Дата добавления: 2018-04-15 ; просмотров: 1888 ; Мы поможем в написании вашей работы!

Источник

КРИТИЧЕСКАЯ СКОРОСТЬ

можно переписать в виде

Полезное

Смотреть что такое «КРИТИЧЕСКАЯ СКОРОСТЬ» в других словарях:

КРИТИЧЕСКАЯ СКОРОСТЬ — скорость вращения вала двигателя, при которой возникает вибрация (колебательное движение) всего двигателя или отдельных его деталей или же вибрация корпуса корабля. См. Критическое число оборотов. Самойлов К. И. Морской словарь. М. Л.:… … Морской словарь

критическая скорость — (a*) Скорость газа, равная местной скорости звука. [ГОСТ 23199 78] [ГОСТ 23281 78] Тематики аэродинамика летательных аппаратов Обобщающие термины характеристики течения газа EN critical velocity … Справочник технического переводчика

критическая скорость — ribinis greitis statusas T sritis Kūno kultūra ir sportas apibrėžtis Greitis, kurį įgyja sportininkas, kai organizmas vartoja maksimalų deguonies kiekį. atitikmenys: angl. ultimate speed vok. Grenzgeschwindigkeit, f; kritische Geschwindigkeit, f… … Sporto terminų žodynas

критическая скорость — ribinis greitis statusas T sritis Kūno kultūra ir sportas apibrėžtis Pats didžiausias greitis, kurį gali įgyti sportininkas (jo varoma priemonė). atitikmenys: angl. ultimate speed vok. Grenzgeschwindigkeit, f; kritische Geschwindigkeit, f rus.… … Sporto terminų žodynas

критическая скорость — kritinis greitis statusas T sritis automatika atitikmenys: angl. critical speed vok. kritische Geschwindigkeit, f rus. критическая скорость, f pranc. vitesse critique … Automatikos terminų žodynas

критическая скорость — kritinis greitis statusas T sritis fizika atitikmenys: angl. critical velocity vok. kritische Geschwindigkeit, f rus. критическая скорость, f pranc. vitesse critique, f … Fizikos terminų žodynas

критическая скорость — kritinis greitis statusas T sritis Energetika apibrėžtis Dujų tekėjimo greitis, lygus vietinei garso greičio vertei tam tikrame dujų srauto pjūvyje. Idealiųjų dujų kritinis greitis priklauso nuo stabdymo temperatūros ir adiabatės rodiklio.… … Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas

КРИТИЧЕСКАЯ СКОРОСТЬ — скорость потока газа в к. л. сечении, равная местному значению скорости звука в газе в данном месте. Для идеального газа К. с. зависит от температуры торможения и показателя адиабаты. Отношение скорости v в произвольном сечении потока к К. с. vк… … Большой энциклопедический политехнический словарь

КРИТИЧЕСКАЯ СКОРОСТЬ — скорость, при которой ламинарное течение жидкости переходит в турбулентное. К. с. прямо пропорциональна коэффициенту кинематической вязкости и числу Рейнольдса (см.) и обратно пропорциональна гидравлическому радиусу (см.) … Словарь по гидрогеологии и инженерной геологии

критическая скорость — Скорость газа в данном месте потока, равная скорости звука в газе в том же месте … Политехнический терминологический толковый словарь

Источник

Рис. 1.50. Схема установки Рейнольдса.

Кроме того было установлено, что процесс перехода одного режима в другой не является полностью обратимым. Ламинарный режим переходит в турбулентный при значительно больших скоростях, чем скорости, при которых турбулентный режим переходит в ламинарный.

Ламинарный режим наблюдается при движении вязких жидкостей.

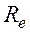
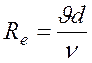
На основании анализа Рейнольдс предложил безразмерный критерий — число Рейнольдса:

, (68)

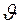
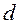
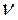
где: — средняя скорость;

— диаметр трубы;

— кинематический коэффициент вязкости.

Число Рейнольдса является условием динамического пособия движущихся потоков жидкости, находящихся только под действием сил внутреннего трения и служит для характеристики потоков независимо от рода движущейся жидкости.

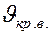
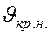
Ламинарный режим переходит в турбулентный при , а турбулентный в ламинарный при .

Из выражения (68) критическая скорость:

, но с учетом того, что получаем:

. (69)

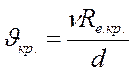
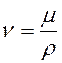
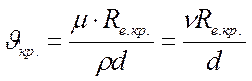
Для трубопроводов работающих полным напором установлено, что:

Для трубопроводов работающих не полным напором или открытых русел, критическое Число Рейнольдса определяется по формуле:

, (70)

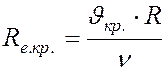
где: 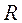— гидравлический радиус.

Для них

Определение режима движения имеет большое значение в практических расчетах.

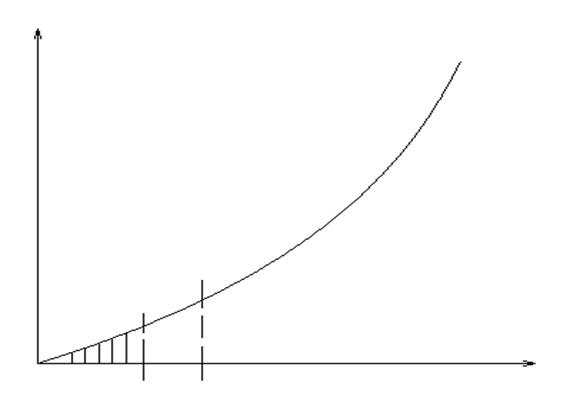
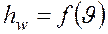
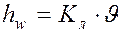
Опыты показывают, что потери напора при ламинарном движении пропорциональны средней скорости течения, т.е. линейная связь:

, (71)

В области турбулентного режима имеем:

, (72)

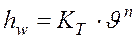
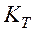
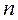
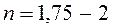
где: — параметр кривой (СД парабола);

— показатель степени ().

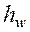
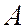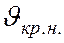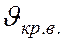Т.е. в области турбулентного режима получаем квадратичную зависимость между и .

Рис. 1.51. График зависимости потерь напора от скорости.

В области ВС – переходная область (режим) используем выражение (1.72.), , точки В и С – критические точки.

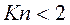
На основании анализа установлен общий закон потерь энергии при движении жидкости.

Гидродинамическое подобие. Критерии подобия.

Полученное ранее число 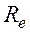имеет большое значение в гидравлике, так как является одним из основных критериев гидродинамического подобия.

Гидродинамическое подобие – это подобие потоков несжимаемой жидкости, включающей в себя подобия геометрические, кинематические и динамические (рис. 1.52.).

Геометрическое подобие – пропорциональность сходственных размеров и равенств углов, т.е. подобие русел.

Кинематическое подобие – это подобие линий тока и пропорциональность сходственных скоростей (обязательно геометрическое подобие русел).

Динамическое подобие – это пропорциональность сил, действующих на сходственные элементы кинематически подобных потоков.

Два потока считаются геометрически подобными, если между их линейными размерами L и l, площадями и , объемами и соблюдаются соотношения:

; ; ; (73)

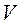
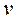
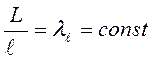
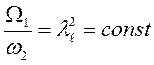
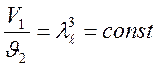
где: — линейный масштаб моделирования.

Две гидравлические системы будут кинематически подобными, если: а) траектории сходственных частиц геометрически подобны;

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Число Рейнольдса

Движение жидкости, несмотря на кажущуюся на первый взгляд, беспорядочность движения имеет определенные закономерности. Рейнольдс в своих опытах нашел определенные общие условия, при которых возможно существование того или иного режима течения и переход от одного режима к другому.

При проведении опытов Рейнольдс в 1883г. подтвердил существование двух режимов течения жидкости. Ему удалось вычислить безразмерное число, описывающее характер потока вязкой жидкости

Содержание статьи

Опыты Рейнольдса

Опыты проводились на специальном лабораторном стенде, который представлял собой заполненный водой бак Б к которому в нижней части присоединена стеклянная трубка Т. На конце трубки установлен кран К для регулирования расхода жидкости. Расход измеряется с помощью секундомера и мерного бочка М. Бак Б постоянно заполняется водой. Над баком Б расположена ёмкость с краской С. По тонкой трубочке Т1 краска попадает в жидкость, движущуюся в трубке Т. Подачу краски регулирует кран Р.

Опыт №1. Немного приоткрываем кран К. При этом в трубке Т начинается движение жидкости. Открываем кран Р и добавляем в жидкость краску. При небольшой скорости движения в трубке Т краска становится прямолинейной и резко выделяющейся в потоке воды цветной струйкой. Эта струйка не перемешивается с остальной жидкостью. Если ввести в жидкость краску несколькими струйками, то они так и будут двигаться не перемешиваясь с остальной водой.

Опыт №2 При намного большем открытии крана струйка краски начинает искривляться и становится волнообразной. Открывая кран ещё больше и увеличивая скорость потока мы увидим, что струйка краски распадается на отдельные вихри и перемешивается с остальной массой воды

Вывод формулы

Рейнольдс установил, что основными факторами, определяющими характер режима являются:
средняя скорость движения жидкости υ,
диаметр трубопровода d,
плотность жидкости ρ,
абсолютная вязкость жидкости μ

При этом чем больше размеры поперечного сечения и плотность жидкости и чем меньше её вязкость, тем легче при увеличении скорости осуществить турбулентный режим.

Для характеристики режима движения жидкости Рейнольдсом был выведен безразмерный параметр Re, учитывающий влияние перечисленных выше факторов, называемый число Рейнольдса. Таким образом формула

Число Рейнольдса и режимы течения.

Границы существования того или иного режима движения жидкости определяются двумя критическими значениями числа Рейнольдса:
нижнее критическое числом Рейнольдса Re_{кр. н.}
верхнее критическое числом Рейнольдса Re_{кр. в.}

Значение скорости, соответствующее этим значениям Re называют критическими.

При значениях числа Рейнольдса Re Re_{кр. в.} – только турбулентный. При Re_{кр. н.} 2300 – всегда турбулентный режимы.

При этом движении жидкости в неустойчивой зоне исключается из особого рассмотрения, это приводит к некоторому запасу и большей надежности в гидравлических расчетах в случае, если в этой зоне действительно имеет место ламинарный режим.

Без особого труда можно получить значения для Reкр для любой формы сечения, а не только круглой формы. Вспоминая, что при круглом сечении радиус

подставляем в формулу для определения числа Рейнольдса

Принимая для критического числа Рейнольдса независимо от формы живого сечения величину Re_кр. = 2300, находим, что для сечения любой формы критериев для сужения о характере режима движения является величина, равная 2300 / 4 = 575.

Таким образом, режим ламинарный если значение числа Рейнольдса

И режим турбулентный, если

Видео по теме.

На практике в большинстве случаев (движение воды в трубах, каналах, реках) приходится иметь дело с турбулентным режимом. Ламинарный режим встречается реже. Он наблюдается, например, при движении в трубах очень вязких жидкостей, что иногда имеет место в нефтепроводах, при движении жидкости в очень узких трубках и порах естественных грунтов.

Источник

Скорость звука, критическая скорость и число Маха

Число Маха является одним из критериев подобия в механике жидкостей и газов. Критерий назван по имени австрийского ученого Эрнста Маха и обозначается буквой М.

Само по себе число Маха является отношением скорости течения в данной точке газового потока к скорости звука.

В этой статье мы собрали для Вас все необходимые теоретические знания и полное описание всего, что касается выводов и понимания скорости звука, критической скорости и числа Маха.

Содержание статьи

Скорость звука

Скорость звука α определяется как скорость распространения малых возмущений (формула 1):

Поскольку процесс распространения малых возмущений можно считать изоэнтропическим (т.е. без теплообмена и потерь)

Где p – давление в среде, н/м 2 ;
ρ – плотность среды, кг/м 3 ;
R – газовая постоянная, нм/кг 0 К;
T – температура, 0 К.
κ – показатель изоэнтропы, равный отношению теплоемкости газа при постоянном давлении к теплоемкости при постоянном объеме определяется по формуле:

Производная от этих уравнений dp/ (p × ρ) определяется с учетом следующих зависимостей.

А если при этом пренебречь влиянием производной dz/dT, то скорость звука будет определяться формулой 2

Величина скорость звука зависит от подвода (или отвода) тепла или механической работы, поскольку может меняться температура газа Т. Но формулы 1 и 2 остаются справедливыми при любом воздействии на газ, не вызывающем химических превращений.

Физически это легко объясняется тем, что изменение давления в плотности и в волне можно рассматривать как малые, но конечные величины, а толщина волны δ столь мала, что её следует считать бесконечно малой.

Поэтому любые массовые силы при переходе через звуковую волну дают слагаемые более высокого порядка малости, чем изменение плотности или давления.

Критическая скорость

Во многих случаях наряду со скоростью звука удобно использовать понятие критической скорости αх, под которой подразумевается местная скорость, равная скорости звука.

Для определения критической скорости воспользуемся общим уравнением сохранения энергии

уравнение критической скорости

Из последних двух равенств получаем, что

где α₀ – скорость звука в неподвижной среде.

Таким образом скорость звука для воздуха

Число Маха

Скорость течения соизмерима со скоростью звука, а в некоторых случаях даже больше её.

В таких случаях важной характеристикой течения является отношение скорости течения к скорости звука.

Формула по которой определяют число Маха выглядит так:

где w – скорость течения в среде
α – скорость звука.

Число Маха является одним из основных критериев подобия течений, определяющих эффект сжимаемости. Ведь как известно при сверхзвуковых скоростях резко изменяется характер течения.

Важное значение числа Маха состоит в том, что оно показывает, превышает ли скорость течения газовой среды скорость звука или нет.

Фактически если М > 1, то значит поток движется со скоростью большей скорости звука.

Тогда в случае М 1 сверхзвуковым. Более того, это не все режимы течения жидкости.

Вот ещё несколько:
Скорость от 1 до 5 Махов, как Вы уже знаете называют сверхзвуковой
От 5 до 23 Махов – гиперзвуковой
Более 23 Мазов – первой космической скоростью.

Хотя число Маха это величина безразмерная, но для понимания его порядка во многих источниках приводится в единицы системы СИ, т.е. требуется представить число маха в километрах в час.

Тогда 1 Мах равен 1 199 км/час или 333 м/сек. Но следует учитывать, что такие величины достигаются при нормальном атмосферном давлении и нулевой температуре и влажности у поверхности земли.

Поскольку давление, температура и влажность изменяются на разной высоте от земли, то изменяется и скорость звука.

Так, например для истребителя летящего на высоте 18 000 м от земли со скоростью 2,3 Маха или 2450 км/час, 1 Мах будет составлять уже 1065 км/час или 295 м/сек.

Источник