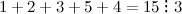Что называется кратным натурального числа
Урок 1 Бесплатно Делители и кратные
Операция деления известна с давних времен.
Привычные нам сегодня обозначения операции деления появлялись постепенно, в более древние времена люди использовали другие знаки.
Первый из символов ( / ), в обиходе косая черта, впервые был применен в 1631 году в одной из работ англичанина Уильяма Отреда.
Со временем в математике стали использовать и знак ( : ). Его в своих работах использовал немецкий математик Готфрид Вильгельм Лейбниц (1646—1716)
При выполнении операции деления используют три математических составляющих:
Сегодня мы познакомимся с делителями и на связанном с ними понятии кратных.
Делители и кратные
Допустим, у вас есть 30 конфет и их надо разделить поровну шести друзьям.
В этом случае 6 друзей получат по 5 конфет, потому что 30 : 6 = 5
Если любое натуральное число делится без остатка на второе натуральное число, то первое называется кратным, а второе называют делителем.
Другими словами, 30 кратно 6, а 6 это делитель 30.
Могут быть и другие варианты решения задачи, которые зависят от данного нам условия.
Если друзей будет 7, тогда раздать всем равное количество конфет не получится, так как 30 без остатка на 7 не делится.
Значит, 30 не кратно 7, и 7 не является делителем 30
Натуральное число, на которое делится без остатка другое число, называется его делителем.
Само число 15 имеет четыре делителя: 1; 3; 5; 15, так как на каждое из этих чисел оно делится без остатка.
Натуральное число, которое делится на другое без остатка, называется его кратным.
Любое натуральное число имеет бесконечно много кратных.
Наименьшим из кратных натурального числа является само это число.
Например, кратными 4 будут числа: 4; 8; 12; 16; 20 и т.д.
У меня есть дополнительная информация к этой части урока!
Существуют числа, равные сумме всех их делителей, не считая самого числа.
Его делители 1, 2, 3.
Само число 6 не учитываем.
Сложив их, получим в сумме 6
К числам с таким свойством можно отнести еще 28 или 496
Пройти тест и получить оценку можно после входа или регистрации
Использование понятий делителя и кратного при решении примеров и задач
Любые математические понятия используются при решении примеров и задач, ответах на вопросы из жизни.
Разберем некоторые из них подробнее.
Пример 1
На сколько равных кучек можно разделить 24 ореха?
Решение:
Нужно выяснить все делители числа 24
Такими будут числа: 1; 2; 3; 4; 6; 8; 12; 24
Каждое из этих чисел будет являться ответом на поставленный вопрос, таким образом:
1 кучка из 24 орехов
2 кучки по 12 орехов
3 кучки по 8 орехов и т.д.
Пример 2
Напишите все двузначные числа, кратные 44
Решение:
Еще нам дано условие, что такие числа должны быть двузначными.
Значит, это два числа 44 и 88.
Оба они делятся на 44 без остатка, в чем можно легко убедиться: 44 : 44 = 1; 88 : 44 = 2
Пример 3
Какое число и кратно 15, и является делителем 15?
Решение:
Оно кратно самому себе и является для себя делителем.
Пример 4
В строю 300 солдат. Можно ли их разделить на 7 равных групп для проведения физической подготовки?
Решение:
Чтобы проверить, можно ли разделить 300 солдат на 7 равных групп, поделим число 300 на 7.
Имеем: 300 : 7 = 42 и в остатке 6. То есть 300 не делится нацело на 7.
Значит, разбить 300 солдат на 7 равных групп не получится.
Пример 5
Докажите, что число 70525 кратно числу 217.
Доказательство:
Выполним деление 70525 на 217 уголком.
Видим, что деление выполнено без остатка, значит, число 70525 кратно числу 217.
У меня есть дополнительная информация к этой части урока!
Делителем любого натурального числа является единица.
И правда, ведь на единицу делится любое натуральное число без остатка
Пройти тест и получить оценку можно после входа или регистрации
Интересная информация
Раньше алгоритм деления в России выглядел совершенно иначе и не имел ничего общего с современным видом.
Например, деление могло получиться в виде полумесяца или по форме напоминать геометрическую фигуру- ромб.
Пусть требуется разделить 598432 на 678
Вот как выглядела запись деления:
1792
5603
5984/
5424
5424
1356
598432 верно разделено
Или разделить 9649378 на 5634:
59417
4015530
9649378
5634444
56333
Заключительный тест
Пройти тест и получить оценку можно после входа или регистрации
Что такое кратное число
Определение кратного числа
Некоторые признаки делимости натуральных чисел
Признак делимости на 2.
Число делится на 2, если его последняя цифра есть число четное (то есть 2, 4, 6, 8) или 0.
Признак делимости на 3.
Число делится на 3, если сумма его цифр делится на 3.
Признак делимости на 4.
Признак делимости на 5.
Число делится на 5, если оно заканчивается либо на 0, либо на 5.
Признак делимости на 8.
Признак делимости на 9.
Число делится на 9, если сумма его цифр делится на 9.
Признак делимости на 11.
Число делится на 11, если сумма цифр, стоящих на четных местах либо равна сумме цифр, стоящих на нечетных местах, либо отличается от неё на число, делящееся на 11.
Признак делимости на 25.
Задание. Среди ниже перечисленных чисел выбрать числа кратные 3:
$$27: 36 ; 58 ; 1119 ; 2345 ; 12354$$
Решение. Будем использовать признак делимости на 3, для этого найдем сумму цифр для каждого числа:
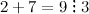


Таким образом, на 3 делятся числа:
$$27 ; 36 ; 1119: 12354$$
Наименьшее общее кратное (НОК)
Общим кратным нескольких натуральных чисел называется натуральное число, являющееся кратным для каждого из них. Наименьшее из всех кратных называется наименьшим общим кратным (НОК).
Алгоритм нахождения наименьшего общего кратного нескольких чисел:
Что такое кратное число не по зубам? Тебе ответит эксперт через 10 минут!
Задание. Найти НОК(360; 420)
Решение. Запишем каноническое разложение заданных чисел:
1. Делители и кратные
Число 12 имеет шесть делителей: 1, 2, 3, 4, 6 и 12.
Число 1 является делителем любого натурального числа.
Любое натуральное число имеет бесконечно много кратных. Например, первые пять чисел, кратных 8, такие: 8, 16, 24, 32, 40. Наименьшим из кратных натурального числа является само это число.
Какое число называют делителем данного натурального числа?
Какое число называют кратным натуральному числу а?
Какое число является делителем любого натурального числа?
Какое число и кратно n, и является делителем n?
1. На сколько равных кучек можно разложить 36 орехов?
2. В каждой коробке лежат 6 чайных ложек. Можно ли, не вскрывая коробок, взять: а) 42 ложки; б) 49 ложек?
а) 5 — делитель 45;
б) 16 — делитель 8;
в) 17 — делитель 152;
г) 27 — кратное 3;
д) 6 — кратное 12;
е) 156 — кратное 13?
4. Является ли число 15 делителем 105? Является ли делителем числа 105 частное 105 : 15?
5. Выберите из чисел 15, 4, 6, 8, 10, 12, 14, 16 те, которые являются:
а) делителями 20;
б) кратными 4;
в) делителями 16 и кратными 4;
г) кратными 3 и делителями 18.
6. Напишите все делители числа:
7. Напишите все двузначные числа, кратные числу:
Кратное
Делимость — одно из основных понятий арифметики и теории чисел, связаное с операцией деления.
Содержание
Определение
Обозначения
Связанные определения
Свойства
Число делителей
Обобщения
Понятие делимости обобщается на произвольные кольца, например кольцо многочленов.
См. также
Полезное
Смотреть что такое «Кратное» в других словарях:
КРАТНОЕ — число, делящееся на данное целое число без остатка, напр. 12 кратно 3. Общее кратное нескольких целых чисел число, делящееся на каждое из них в отдельности, напр. 180 общее кратное чисел 30, 18, 2. При арифметических действиях особое значение… … Большой Энциклопедический словарь
кратное — ого; ср. Целое число, делящееся на данное без остатка. Шесть к. чисел два и три. Наименьшее общее к. нескольких чисел. * * * кратное число, делящееся на данное целое число без остатка, например 12 кратно 3. Общее кратное нескольких целых чисел … … Энциклопедический словарь
Кратное — натурального (целого положительного) числа а, натуральное число, делящееся на а без остатка. Так, 156 есть К. 13, тогда как 108 не является К. 13. Число n, которое делится на каждое из чисел а, b. m, называется общим К. этих чисел. Из … Большая советская энциклопедия
Кратное — ср. Целое число, делящееся на какое либо число без остатка. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
КРАТНОЕ — число, делящееся на данное целое число без остатка, напр. 12 кратно 3. Общее К. неск. целых чисел число, делящееся на каждое из них в отдельности, напр. 180 общее К. чисел 30, 18, 2. При арифметич. действиях особое значение имеет наименьшее общее … Естествознание. Энциклопедический словарь
кратное — кр атное, ого … Русский орфографический словарь
кратное — ого; ср. Целое число, делящееся на данное без остатка. Шесть кра/тное чисел два и три. Наименьшее общее кра/тное нескольких чисел … Словарь многих выражений
кратное (число) — кратный многократный множественный составной параллельный — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы… … Справочник технического переводчика
Делимость натуральных чисел.
Деление – это действие, обратное умножению. Рассмотрим более подробно деление натуральных чисел.
Натуральными числами называют числа, используемые для счета. Каждому количеству предметов счета соответствует некоторое натуральное число. Если предметов для счета нет, то используется число 0, но при счете предметов мы никогда не начинают с 0, и соответственно число 0 нельзя отнести к натуральным. Понятно, что наименьшим натуральное число является единица. Наибольшего натурального числа не существует, потому что каким бы большим не было число, всегда можно прибавить к нему 1 и записать следующее натуральное число.
Натуральное число k делится нацело на натуральное число n, если найдётся такое натуральное число m, для которого справедливо равенство k =n • m.
Или другими словами, чтобы разделить одно число на другое, надо найти такое трете число, которое при умножении на второе дает первое
число n — делителем числа k.
Числа 1, 2, 3, 6, 10, 15, 30 также являются делителями числа 30, а число 30 является кратным каждого из этих чисел. Заметим, что число 30 не делится нацело, например, на число 7. Поэтому число 7 не является делителем числа 30, а число 30 не кратно числу 7.
Выполнив действия по делению говорят: «Число k делится нацело на число n», «Число n является делителем числа k», «Число k кратно числу n», «Число k является кратным числа n».
Легко записать все делители числа 6. Это числа 1, 2, 3 и 6. А можно ли перечислить все числа, кратные числу 6? Числа 6• 1, 6• 2, 6• 3, 6• 4, 6• 5 и т. д. кратны числу 6. Получаем, что чисел, кратных числу 6, — бесконечно много. Поэтому перечислить их все невозможно.
Вообще, для любого натурального числа k каждое из чисел
является кратным числа k.
Наименьшим делителем любого натурального числа k является число 1, а наибольшим делителем — само число k.
Среди чисел, кратных числу k, наибольшего нет, а наименьшее есть — это само число k.
Каждое из чисел 21 и 36 делится нацело на число 3, и их сумма, число 57, также делится нацело на число 3. Вообще, если каждое из чисел k и n делится нацело на число m, то и сумма k + n также делится нацело на число m.
Каждое из чисел 4 и 8 не делится нацело на число 3, а их сумма, число 12, делится нацело на число 3. Каждое из чисел 9 и 7 не делится нацело на число 5, и их сумма, число 16, не делится нацело на число 5. Вообще, если ни число k, ни число n не делятся нацело на число m, то сумма k + n может делиться, а может и не делиться нацело на число m.
Число 35 делится без остатка на число 7, а число 17 на число 7 нацело не делится. Сумма 35 + 17 нацело на число 7 также не делится. Вообще, если число k делится нацело на число m и число n не делится нацело на число m, то сумма k + n не делится нацело на число m.