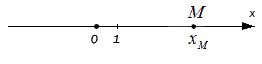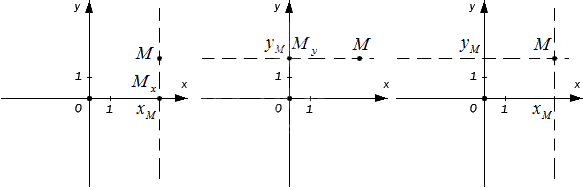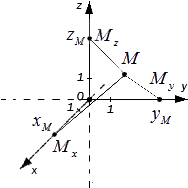Что называется координатами вектора в прямоугольной системе координат

Вектор. Координаты вектора.

Формула определения координат вектора для двухмерных задач.

В случае двухмерной задачи вектор с известными координатами точек A(х₁;у₁) и B(x₂;y₂) можно вычислить:

= (x₂ – x₁ ; y₂ – y₁).

Формула определения координат вектора для пространственных задач.

В случае пространственной задачи вектор с известными координатами точек A(х₁;у₁;z₁) и B(x₂;y₂;z₂) можно вычислить применив формулу:

= (x₂ – x₁ ; y₂ – y₁;z₂ – z₁).

Координаты дают всеобъемлющую характеристику вектора, поскольку по координатам есть возможность построить и сам вектор. Зная координаты, легко вычислить и длину вектора. (Свойство 3, приведенное ниже).

Свойства координат вектора.

1. Любые равные векторы в единой системе координат имеют равные координаты.

2. Координаты коллинеарных векторов пропорциональны. При условии, что ни один из векторов не равен нулю.

3. Квадрат длины любого вектора равен сумме квадратов его координат.

4.При операции умножения вектора на действительное число каждая его координата умножается на это число.

5. При операции сложения векторов вычисляем сумму соответствующие координаты векторов.

6. Скалярное произведение двух векторов равняется сумме произведений их соответствующих координат.

Источник

Прямоугольная система координат на плоскости и в пространстве

При введении системы координат на плоскости или в трехмерном пространстве появляется уникальная возможность описания геометрических фигур и их свойств при помощи уравнений и неравенств. Это имеет иное название – методы алгебры.

Данная статья поможет разобраться с заданием прямоугольной декартовой системой координат и с определением координат точек. Более наглядное и подробное изображение имеется на графических иллюстрациях.

Прямоугольная декартова система координат на плоскости

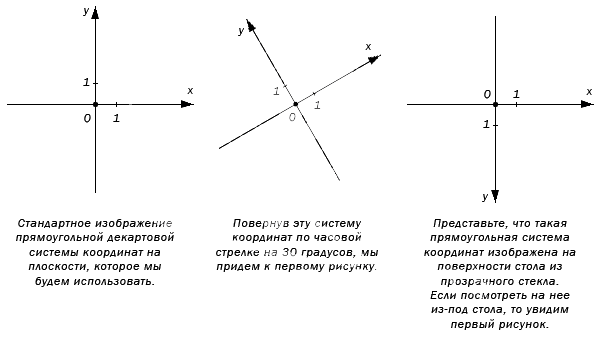
Изображение прямоугольной системы координат на плоскости.

Оси абсцисс и ординат имеют одинаковую единицу изменения и масштаб, что показано в виде штрихе в начале координатных осей. Стандартное направление О х слева направо, а O y – снизу вверх. Иногда используется альтернативный поворот под необходимым углом.

Прямоугольная система координат получила название декартовой в честь ее первооткрывателя Рене Декарта. Часто можно встретить название как прямоугольная декартовая система координат.

Прямоугольная система координат в трехмерном пространстве

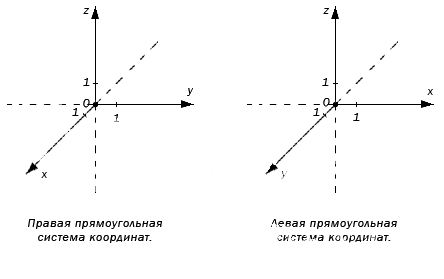
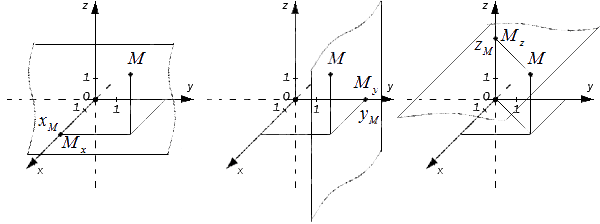
По направлению координатных осей делят на правую и левую прямоугольные системы координат трехмерного пространства.

Аналогично образуется левая система координат. Обе системы совместить невозможно, так как соответствующие оси не совпадут.

Координаты точки в декартовой системе координат на плоскости

Имеющееся число x M называют координатой точки М на заданной координатной прямой.

Координаты точки в прямоугольной системе координат в трехмерном пространстве

Источник

Координаты вектора в декартовой системе координат (ДСК)

Для начала дадим определение координат вектора в заданной системе координат. Чтобы ввести данное понятие, определим что мы называем прямоугольной или декартовой системой координат.

Прямоугольная система координат представляет из себя прямолинейную систему координат с взаимно перпендикулярными осями на плоскости или в пространстве.

С помощью введения прямоугольной системы координат на плоскости или в трехмерном пространстве становится возможным описывание геометрических фигур вместе с их свойствами при помощи уравнений и неравенств, то есть использовать алгебраические методы при решении геометрических задач.

Тем самым, мы можем привязать к заданной системе координат векторы. Это значительно расширит наши возможности при решении определенных задач

Координатные векторы

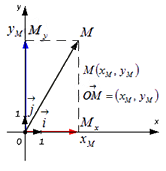
Векторы i → и j → называются координатными векторами для заданной системы координат.

Разложение вектора

Коэффициенты a x и a y называются координатами вектора в данной системе координат на плоскости.

Следует обратить внимание, что порядок записи координат, имеет важное значение, если вы запишите координаты вектора в другом порядке, вы получите совершенно другой вектор.

Равные и противоположные векторы

Векторы a → и b → равны тогда, когда их соответствующие координаты равны.

Противоположным вектором называется вектор противоположный данному.

Координаты радиус-вектора точки

Чтобы ввести данное определение, требуется показать в данной системе координат связь координат точки и координат вектора.

Вектор O M → называется радиус-вектором точки M .

Определим, какие координаты в данной системе координат имеет радиус-вектор точки

Иначе говоря, координаты радиус-вектора точки М равны соответствующим координатам точки М в прямоугольной декартовой системе координат.

Источник

Что называется координатами вектора в прямоугольной системе координат

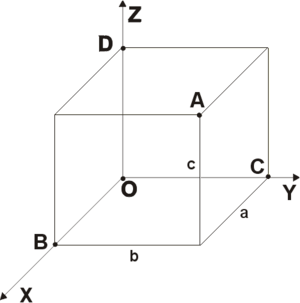
Если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление (оно обозначается стрелкой) и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в пространстве.
Прямые с выбранными на них направлениями называются осями координат, а их общая точка — началом координат. Она обозначается обычно буквой О.
Оси координат обозначаются так: Ох, Оу, Оz — и имеют названия: ось абсцисс, ось ординат, ось аппликат. Вся система координат обозначается Охуz.
Плоскости, проходящие соответственно через оси координат Ох и Оу, Оу и Оz, Оz и Ох, называются координатными плоскостями и обозначаются Оху, Оуz, Оzх.
Точка О разделяет каждую из осей координат на два луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч отрицательной полуосью.

Если точка А (х; у; z) лежит на координатной плоскости или на оси координат, то некоторые ее координаты равны нулю.

Источник

Прямоугольная система координат

Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Очень легко и прямо обобщается для пространств любой размерности, что также способствует ее широкому применению.

Содержание

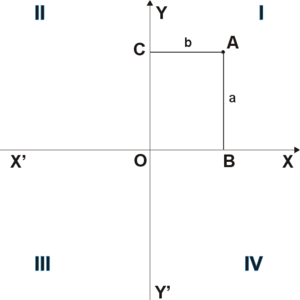
Прямоугольная система координат на плоскости

Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат и . Оси координат пересекаются в точке , которая называется началом координат, на каждой оси выбрано положительное направление.

Положение точки на плоскости определяется двумя координатами и . Координата равна длине отрезка , координата — длине отрезка в выбранных единицах измерения. Отрезки и определяются линиями, проведёнными из точки параллельно осям и соответственно.

При этом координате приписывается знак минус, если точка лежит на луче (а не на луче , как на рисунке). Координате приписывается знак минус, если точка лежит на луче . Таким образом, и являются отрицательными направлениями осей координат (каждая ось координат рассматривается как числовая ось).

Координата называется абсциссой точки , координата — ординатой точки .

Символически это записывают так:

или указывают принадлежность координат конкретной точке с помощью индекса:

Прямоугольная система координат в пространстве

Прямоугольная система координат в пространстве (в этом параграфе имеется в виду трехмерное пространство, о более многомерных пространствах — см. ниже) образуется тремя взаимно перпендикулярными осями координат , и . Оси координат пересекаются в точке , которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно (не обязательно [2] ) одинаковы для всех осей. — ось абсцисс, — ось ординат, — ось аппликат.

Положение точки в пространстве определяется тремя координатами , и . Координата равна длине отрезка , координата — длине отрезка , координата — длине отрезка в выбранных единицах измерения. Отрезки , и определяются плоскостями, проведёнными из точки параллельно плоскостям , и соответственно.

Координата называется абсциссой точки , координата — ординатой точки , координата — аппликатой точки .

Символически это записывают так:

или привязывают запись координат к конкретной точке с помощью индекса:

Каждая ось рассматривается как числовая прямая, т. е. имеет положительное направление, а точкам, лежащим на отрицательном луче приписываются отрицательные значения координаты (расстояние берется со знаком минус). То есть, если бы, например, точка лежала не как на рисунке — на луче , а на его продолжении в обратную сторону от точки (на отрицательной части оси ), то абсцисса точки была бы отрицательной (минус расстоянию ). Аналогично и для двух других осей.

Прямоугольные все системы координат в трехмерном пространстве делятся на два класса — правые (также используются термины положительные, стандартные) и левые. Обычно по умолчанию стараются использовать правые координатные системы, а при их графическом изображении еще и располагать их если можно, в одном из нескольких обычных (традиционных) положений. (На рис. 2 изображена правая координатная система). Правую и левую системы координат невозможно поворотами [3] совместить так, чтобы совпали соответствующие оси (и их направления). Определить, к какому классу относится какая-либо конкретно взятая система координат можно используя правило правой руки, правило винта итп (положительное направление осей выбирают так, чтобы при повороте оси против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси , если этот поворот наблюдать со стороны положительного направления оси ).

Прямоугольная система координат в многомерном пространстве

Прямоугольная система координат может быть использована и в пространстве любой конечной размерности аналогично тому, как это делается для трехмерного пространства. Количество координатных осей при этом равно размерности пространства (в этом параграфе будем обозначать ее n).

Для обозначения координат обычно [4] применяют не разные буквы, а одну и ту же букву с числовым индексом. Чаще всего это:

Для обозначения произвольной i-ой координаты из этого набора используют буквенный индекс:

а нередко обозначение используют и для обозначения всего набора, подразумевая, что индекс пробегает весь набор значений: .

Прямоугольные координаты вектора

Для векторов (направленных отрезков), начало которых не совпадает с началом координат, прямоугольные координаты можно определить одним из двух способов:

2. Вместо этого можно просто вычесть из координат конца вектора (направленного отрезка) координаты его начала.

В прямоугольных координатах очень просто записываются все операции над векторами:

а отсюда и вычитание и деление:

(Это верно для любой размерности n и даже, наравне с прямоугольными, для косоугольных координат).

(Только в прямоугольных координатах с единичным масштабом по всем осям).

для любой размерности пространства,

Очевидно, всё это позволяет, если надо, свести все операции над векторами к достаточно простым операциям над числами.

В трёхмерном случае такие орты обычно обозначаются

, и

, и .

Могут также применяться обозначения со стрелками (, и или , и ) или другие в соответствии с обычным способом обозначения векторов в той или иной литературе.

При этом в случае правой системы координат действительны следующие формулы с векторными произведениями ортов:

Для более высоких, чем 3, размерностей (или для общего случая, когда размерность может быть любой) обычно для ортов применяют вместо этого обозначения с числовыми индексами, достаточно часто [10] это

Вектор любой размерности раскладывается по базису (координаты служат коэффициентами разложения):

а для ортонормированного базиса координаты еще и очень легко найти через скалярные произведения с ортами:

История

Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости.

Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.

Использование ортов восходит, по-видимому, к Гамильтону и Максвеллу.

Источник