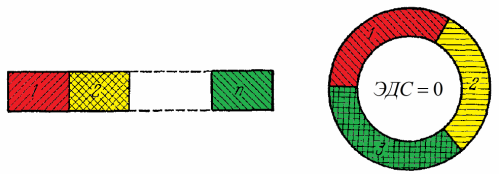
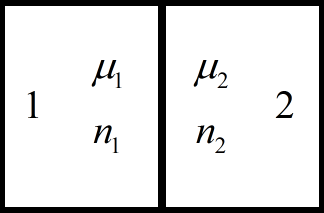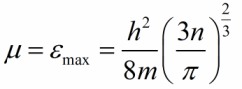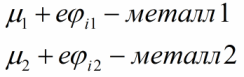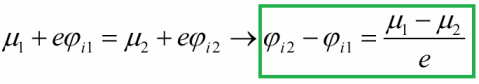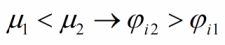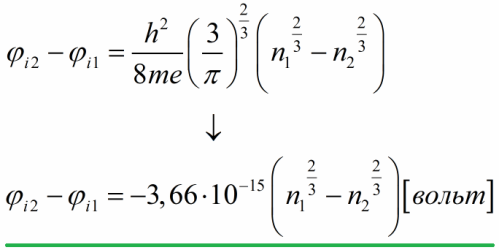Что называется контактной разностью потенциалов
Контактная разность потенциалов
Если два образца, изготовленные из двух разных металлов, плотно прижать друг к другу, то между ними возникнет контактная разность потенциалов. Итальянский физик, химик и физиолог Алессандро Вольта обнаружил данный феномен в 1797 году, занимаясь изучением электрических свойств металлов.
Вольта установил тогда, что если соединить металлы в цепь в таком порядке: Al, Zn, Sn, Pb, Bi, Hg, Fe, Cu, Ag, Au, Pt, Pd, то каждый следующий металл в полученной цепочке обретет потенциал ниже предыдущего. Кроме того ученый выяснил, что несколько металлов, объединенные таким способом, дадут одну и ту же разность потенциалов между концами образованной цепи, независимо от последовательности расположения данных металлов в этой цепи — это положение известно теперь как закон последовательных контактов Вольта.
Здесь крайне важно понимать, что для точного выполнения закона последовательности контактов необходимо, чтобы вся цепочка металлов находилась при одной и той же температуре.
Для различных пар металлов контактная разность потенциалов будет своей определенной, из диапазона от десятых и сотых долей вольта до единиц вольт.
Чтобы понять причину появления контактной разности потенциалов, удобно воспользоваться моделью свободных электронов.
Пусть оба металла пары находятся при абсолютно нулевой температуре, тогда все уровни энергии, включая границу Ферми, окажутся заполнены электронами. Значение энергии (границы) Ферми связано с концентрацией электронов проводимости в металле следующим соотношением:
Принимая во внимание данное соотношение, приведем в плотный контакт два металла с разными энергиями Ферми, и следовательно с разными концентрациями электронов проводимости.
Допустим для нашего примера, что второй металл имеет большую концентрацию электронов проводимости, и соответственно уровень Ферми у второго металла выше чем у первого.
Тогда при соприкосновении металлов друг с другом начнется диффузия (проникновение из одного металла — в другой) электронов из металла 2 — в металл 1, ведь в металле 2 есть заполненные энергетические уровни, которые находятся выше уровня Ферми первого металла, значит электроны с этих уровней станут заполнять в металле 1 свободные верхние уровни.
Обратное движение электронов в такой ситуации энергетически невозможно, ведь во втором металле все нижележащие уровни энергии уже полностью заполнены. В конце концов металл 2 зарядится положительно, а металл 1 — отрицательно, при этом уровень Ферми первого металла станет выше чем был, а у второго металла — снизится. Изменение это будет таковым:
В результате между контактирующими металлами возникнет разность потенциалов, и соответствующее ей электрическое поле, которое теперь станет препятствовать дальнейшей диффузии электронов.
Ее процесс полностью остановится, когда разность потенциалов достигнет определенной величины, соответствующей равенству уровней Ферми двух металлов, при котором в металле 1 не останется свободных уровней для вновь поступающих электронов из металла 2, а в металле 2 так и не освободятся уровни для возможности миграции электронов из металла 1. Наступит энергетическое равновесие:
Поскольку заряд электрона отрицателен, то будем иметь следующее положение относительно потенциалов:
Хотя изначально мы и приняли температуру металлов равной абсолютному нулю, тем не менее аналогичным образом равновесие будет наступать при любой температуре.
Энергия Ферми при наличии электрического поля будет ни чем иным как химическим потенциалом единственного электрона в электронном газе, отнесенным к заряду этого самого единичного электрона, а так как в условиях равновесия химические потенциалы электронных газов обеих металлов будут равны, то стоит лишь добавить в рассмотрение зависимость химического потенциала от температуры.
Итак, рассмотренная нами разность потенциалов называется внутренней контактной разностью потенциалов и удовлетворяет закону последовательных контактов Вольта.
Давайте оценим данную разность потенциалов, для этого выразим энергии Ферми через концентрации электронов проводимости, после чего подставим численные значения констант:
Таким образом, на базе модели свободных электронов, внутренняя контактная разность потенциалов для металлов имеет порядок величин от сотых долей вольта до единиц вольт.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ
Если составить электрич. цепь из неск. разл. проводников, то К. р. п. между крайними проводниками определяется только их работами выхода и не зависит от промежуточных членов цепи (правило Вольта) К. р. п. может достигать неск. В. Она зависит от строения проводника (его объёмных электронных свойств) и от состояния его поверхности. Поэтому К. р. п можно изменять обработкой поверхностей (покрытия ми, адсорбцией и т. п.), введением примесей (для полупроводников) и сплавлением с др. веществами (в случае металлов).
Электрич. поле К. р. п., создаваемое приконтактным объёмным зарядом, сосредоточено вблизи границы раздела и в зазоре между проводниками. Протяжённость приконтактной области тем меньше, чем больше концентрации электронов проводимости в проводниках: в металлах 

Электрич. поле К. р. п. изменяет концентрации свободных носителей заряда (электронов, дырок) в при-контактном слое. Когда концентрация осн. носителей заряда в полупроводниках понижается, приконтактный слой представляет собой область повыш. сопротивления (запирающий слой). Т. к. концентрация носителей и, следовательно, сопротивление контакта изменяются несимметрично в зависимости от знака приложенного напряжения, то контакт двух полупроводников обладает вентильным (выпрямляющим) свойством. С К. р. п. связаны также вентильная фотоэдс, термоэлектричество и ряд др. электронных явлений. На существовании
Лит.: Ландау Л. Д., Л и ф ш и ц Е. М., Электродинамика сплошных сред, 2 изд., М., 1982, p 23; П и к у с Г. Е., Основы теории полупроводниковых приборов, М., 1965.
Полезное
Смотреть что такое «КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ» в других словарях:
Контактная разность потенциалов — это разность потенциалов, возникающая при соприкосновении двух различных проводников, имеющих одинаковую температуру. Содержание 1 Описание 2 Объяснения 3 Опыт Вольты … Википедия
Контактная разность потенциалов — разность электрических потенциалов, возникающая между контактирующими телами в условиях термодинамического равновесия. Наиболее важно понятие К. р. п. для твёрдых проводников (металлов (См. Металлы) и полупроводников (См. Полупроводники)) … Большая советская энциклопедия
КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ — равновесная разность потенциалов между двумя разнородными металлами, полупроводниками или металлом и полупроводником, возникающая в случае их непосредственного (см.) друг с другом при данной температуре. К. р. п. встречается в термопарах,… … Большая политехническая энциклопедия
контактная разность потенциалов — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN contact potential differencework function differencecontact… … Справочник технического переводчика
контактная разность потенциалов — 3.1 контактная разность потенциалов; КРП: Разность потенциалов, возникающая между контактирующими проводниками. Источник … Словарь-справочник терминов нормативно-технической документации
контактная разность потенциалов — разность электрических потенциалов U, возникающая между двумя контактирующими проводниками в условиях термодинамического равновесия: U = (φ1 φ2)/е, где φ1 и φ2 работы выхода проводников, е заряд электрона. В электрической цепи из нескольких… … Энциклопедический словарь
контактная разность потенциалов — sąlyčio potencialų skirtumas statusas T sritis fizika atitikmenys: angl. contact drop; contact potential difference vok. Kontaktpotentialdifferenz, f rus. контактная разность потенциалов, f pranc. différence de potentiel de contact, f … Fizikos terminų žodynas
КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ — разность электрич. потенциалов U, возникаю щая между двумя контактирующими проводни ками в условиях термодинамич. равновесия U = (ф1 ф2)/е, где ф1 и ф2 работы выхода проводников, е заряд электрона. В электрич цепи из неск. проводников разность… … Естествознание. Энциклопедический словарь
контактная разность потенциалов — Разность работ выхода электрона для двух тел, находящихся в электрическом контакте … Политехнический терминологический толковый словарь
Контактная разность потенциалов
Потенциальность электростатического поля
Электрическое поле с напряженностью \( \vec
где \( d \) – расстояние, на которое перемещается заряд, \( \alpha \) – угол между векторами напряженности электрического поля и перемещения заряда.
Важно! Эта формула применима для нахождения работы только в однородном электростатическом поле. Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только начальным и конечным положением заряда
Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только начальным и конечным положением заряда.
Потенциальным называется поле, работа сил которого по перемещению заряда по замкнутой траектории равна нулю.
Важно! Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю. Электростатическое поле является потенциальным
Работа электростатического поля по перемещению заряда равна изменению потенциальной энергии, взятому с противоположным знаком. В электродинамике энергию принято обозначать буквой \( W \), так как буквой \( E \) обозначают напряженность поля:
Потенциальная энергия заряда \( q \), помещенного в электростатическое поле, пропорциональна величине этого заряда. Потенциальная энергия взаимодействия зарядов вычисляется относительно нулевого уровня (аналогично потенциальной энергии поля силы тяжести). Выбор нулевого уровня потенциальной энергии определяется исходя из соображений удобства при решении задачи.
Возникновение — контактная разность — потенциал
Возникновение контактной разности потенциалов происходит прежде всего потому, что различные металлы характеризуются разной работой выхода. Электроны легче переходят из металла, для которого работа выхода имеет меньшее значение, в металл, для которого работа имеет большее значение, чем в обратном направлении. Первый металл заряжается положительно, второй отрицательно. При этом на их границе возникает двойной слой разноименных зарядов, внутри которого существует сильное электрическое поле. Легко понять, что это поле будет тормозить дальнейший переход электронов из первого металла во второй и в то же время способствовать их обратному переходу. В результате между этими двумя процессами устанавливается динамическое равновесие, при котором напряженность поля в двойном слое, а следовательно, и разность потенциалов, до которой заряжаются металлы, достигает максимального значения.
Возникновение контактной разности потенциалов происходит вследствие двух причин: 1) разная работа выхода электронов, у различных металлов. Металл, имеющий меньшее значение работы выхода электронов, легче их теряет и заряжается положительно, а металл с большей работой выхода накапливает электроны и заряжается отрицательно.
| Энергетическая диаграмма возникновения внешней контактной разности.| Энергетическая диаграмма возникновения вну. |
Возникновение контактной разности потенциалов в случае контакта металл-полупроводник принципиально не отличается от контакта металл-металл, так как она будет определяться разностью работ выхода металла и полупроводника. Однако отличие свойств полупроводника от металла, обусловленное возможностью значительного изменения концентраций носителей заряда в полупроводниках, приводит к возникновению специфических явлений на контакте металл-полупроводник.
Возникновение контактной разности потенциалов между соприкасающимися металлическими проводниками было открыто в конце XVI11 в.
| Схема, поясняющая контактную разность потенциалов в. |
Возникновение контактной разности потенциалов определяется следующим процессом. При соприкосновении металлов в месте их контакта происходит взаимное перемещение электронов.
| Вольт-амперная характеристика полупроводникового диода. |
Объясните возникновение контактной разности потенциалов в контакте двух металлов и двух полупроводников.
Рассмотрим возникновение контактной разности потенциалов при контакте полупроводника и металла.
| К объяснению контактной разности потенциалов. |
| Характеристики р-ге-перехода. |
С другой стороны, возникновение контактной разности потенциалов и электрического поля в переходе приводит к появлению тока проводимости, направленного навстречу диффузионному току. Ток проводимости образуется за счет дрейфа через переход дырок из области с электропроводностью n — титга, где они являются неосновными носителями, в область с электропроводностью р-типа и дрейфа электронов через переход из области с электропроводностью р-типа в область с электропроводностью л-типа. В установившемся режиме при отсутствии внешнего напряжения, поданного на пластину с p — n — переходом, между обоими токами ( проводимости и диффузионным) устанавливается динамическое равновесие. И так как они направлены навстречу друг другу, общий ток через пластину и переход равен нулю. Высота потенциального барьера автоматически устанавливается такой, чтобы было равновесие между двумя токами.
Все остальные энергетические уровни после возникновения контактной разности потенциалов должны соответственно изогнуться. При этом энергетический уровень потолка верхней свободной зоны должен быть непрерывным. Обычно энергетический уровень потолка верхней свободной зоны является энергетическим уровнем потолка зоны проводимости, так как свободные энергетические зоны перекрываются друг с другом.
Решение задачи:
Зная, что заряженная частица была ускорена разностью потенциалов \(U\), её скорость \(\upsilon\) можно найти по закону сохранения энергии:
На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца \(F_Л\), которую определяет следующая формула:
Здесь \(B\) – индукция магнитного поля, \(\upsilon\) – скорость частицы, \(q\) – модуль заряда частицы, \(\alpha\) – угол между вектором скорости и вектором магнитной индукции (\(\alpha=90^\circ\), так как по условию поле поперечное).
Направление действия силы Лоренца определяется правилом левой руки: если ладонь левой руки расположить так, чтобы линии магнитной индукции входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (или против направления отрицательного заряда), то большой палец, оставленный на 90°, покажет направление силы Лоренца. Пусть мы имеем дело с положительно заряженной частицей, тогда в нашем случае (при таком направлении вектора магнитной индукции) сила Лоренца будет направлена вниз (имеется ввиду направление силы Лоренца в точке 1).
Сила Лоренца \(F_Л\) сообщает частице центростремительное ускорение \(a_ц\), поэтому из второго закона Ньютона следует, что:
Центростремительное ускорение \(a_ц\) можно определить через скорость \(\upsilon\) и радиус кривизны траектории \(R\) по формуле:
Подставим (4) в (3), тогда:
Приравняем правые части (2) и (5):
Учитывая (1), получим:
Возведем в квадрат обе части этого равенства:
Откуда искомое отношение заряда частицы к массе \(\frac
Очевидно, что расстояние между точками 1 и 2 равно диаметру окружности, по которой движется заряженная частица в магнитном поле. Известно, что радиус окружности равен половине диаметра, то есть \(R= \frac
Проводники в электростатическом поле
Размещение проводника в электростатическом поле приводит к тому, что поле начнет действовать на носители заряда внутри проводящего предмета. Носители начинают перемещаться до тех пор, пока электростатическое поле вне поверхности ни обратится в нуль.
Поскольку поле внутри вещества отсутствует, то во всех точках проводящего материала энергия будет постоянной, а поверхность эквипотенциальной. Векторы напряженности поля направлены под прямым углом в любой точке поверхности проводника.

Под действием поля заряды внутри проводника отсутствуют, поскольку они сосредоточены исключительно на поверхности. Этот факт используется при экранировке – защите тел от влияния внешних электромагнитных и электростатических полей. Для экранирования может использоваться не только сплошной проводящий материал, но и сетка, так называемая «клетка Фарадея».

Также свойство перемещения заряженных частиц (электронов) используется в электростатических генераторах для получения напряжения в несколько миллионов вольт.
Примеры формул для вычисления напряжения
Измерить напряжение можно, воспользовавшись такой формулой:
U=A/q (U, A и q – величина напряжения, переносящая работа электрополя и заряд, соответственно).
Выразив работу (A=q*U), можно понять, что, чем больше напряженность, тем большую работу потребуется совершить электрополю, чтобы перенести Q
Такие преобразования помогают усвоить, почему важно, чтобы источник питания был мощным. Чем больше потенциальная разница между его клеммами, тем больший объем работы он способен обеспечивать
Чтобы определить напряжение на участке электрической цепи, используется следующее выражение:
Здесь I – сила протекающего по проводнику электротока, R – сопротивление фрагмента цепи. Для последовательно и параллельно соединенных проводниковых элементов также существуют свои законы, согласно которым рассчитываются напряжение, токовая сила и сопротивление для каждой из веток.
КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ
Если поверхность одного металла (1) привести соприкосновение (контакт) с поверхностью другого металла (2), то происходит переход электронов из одного металла в другой, вследствие чего один из них заряжается положительно, другой — отрицательно. Возникающая при этом разность потенциалов между соприкасающимися телами называется контактной разностью потенциалов.
Появление контактной разности потенциалов обусловлено двумя причинами:
1) различием в работах выхода электрона из металлов, приведенных в соприкосновение. В этом случае силы, действующие на электроны в пограничной области со стороны ионных каркасов обоих Металлов (направленные в противоположные стороны), не уравновешены и поэтому вызывают переход электронов из одного металла в другой;
2) различием в плотностях электронного газа в металлах, вследствие чего возникает диффузный переход электронов из металла, где плотность этого газа большая, в металл, где эта плотность меньше.
Рассмотрим действие каждой из этих причин в отдельности. На электрон, оказавшийся в пограничной области (между ионными решетками обоих металлов), действуют электрические поля созданные поверхностными слоями каждого из металлов (рис. III.35) и направленные в противоположные стороны. Сумма векторов лишь в частном случае может оказаться равной нулю в какой-нибудь точке пограничного слоя. При сложной зависимости этих векторов от расстояния (см. рис. 111.34) их сумма на всем протяжении пограничного слоя будет отлична от нуля и поэтому на электрон, оказавшийся в этой области, действует некоторая результирующая сила, направленная в сторону одного из металлов.
На рис. III.35 показаны ионные решетки двух металлов 1 и 2 с различными объемными плотностями ионов. Очевидно, на электроны, оказавшиеся в пограничной области, со стороны металла 1 действуют меньшие силы, чем со стороны металла 2, имеющего более плотную ионную решетку; работа выхода электрона из металла будет Меньше, чем из металла Если то вследствие теплового движения оба металла посылают в пограничный слой (в единицу времени с единицы поверхности) одинаковое число электронов Из этих электронов большая часть Втягивается в металл 2. Таким образом, из пограничного слоя металл 1 получает меньше электронов, чем посылает сам, а металл 2 — больше; первый заряжается положительно, второй — отрицательно. Это вызовет появление в пограничной области внешнего электрического поля направленного от положительно заряженного металла к отрицательно заряженному; оно будет
Потенциал. Разность потенциалов. ЗАДАЧИ с решениями
Формулы, используемые на уроках «Решение задач на тему: Работа перемещения заряда в электрическом поле. Потенциал. Разность потенциалов» для подготовки к ЕГЭ.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Металлический шар диаметром d заряжен с поверхностной плотностью зарядов σ. Найти потенциал φ этого шара, если он окружен заземленной проводящей сферой, имеющей общий с шаром центр. Диаметр сферы D. Среда — воздух.
Задача № 2.
Потенциал заряженного шара φ1 = 300 В. Чему равен потенциал φ2 электрического поля этого шара в точке, отстоящей на расстоянии l = 50 см от его поверхности, если радиус шара R = 25 см?
Задача № 3.
Определить потенциал φ точки поля, находящейся на расстоянии а = 9 см от поверхности заряженного шара радиусом R = 1 см, если поверхностная плотность зарядов на шаре σ = 1 • 10–11 Кл/см2. Среда — воздух.
Задача № 4.
В точке 1 поля точечного заряда-источника потенциал φ1 = 40 В, а в точке 2 φ2 = 10 В. Найти потенциал φ в точке М, лежащей посередине между точками 1 и 2 (рис. 3-6).
Задача № 5.
В трех вершинах квадрата со стороной а = 20 см находятся заряды q1 = 1 • 10–8 Кл, q2 = 2 • 10–8 Кл и q3 = 2 • 10–8 Кл (рис. 3-7). Определить потенциал φ электрического поля, созданного этими зарядами в четвертой вершине.
Задача № 6.
Четыре одинаковых точечных заряда q расположены на одной прямой на расстоянии r друг от друга. Какую работу А надо совершить, чтобы переместить эти заряды в вершины тетраэдра со стороной r? Среда — вакуум.
Задача № 7.
Два одинаково заряженных шарика диаметрами d = 0,5 см каждый расположены на расстоянии l = 2 см между их поверхностями (рис. 3-14). До какого потенциала φ они заряжены, если сила их отталкивания друг от друга F = 2 мкН? Среда — воздух.
Задача № 8.
В однородном электрическом поле напряженностью Е = 2 кВ/см переместили заряд q = –20 нКл в направлении силовой линии поля на расстояние d = 10 см. Найти работу поля А, изменение потенциальной энергии поля ΔWп и напряжение (разность потенциалов) U между начальной и конечной точками перемещения.
Задача № 9.
Между двумя горизонтальными плоскостями, заряженными разноименно и расположенными на расстоянии d = 5 мм друг от друга, находится в равновесии капелька масла массой 20 нг (нанограмм) (рис. 3-10). Найти число избыточных электронов N на этой капельке. Среда — воздух. Разность потенциалов между плоскостями U = 2 кВ.
Задача № 10.
На пластине М поддерживается потенциал φ1 = +80 В, а на пластине N – φ2 = –80 В (рис. 3-11, а). Расстояние между пластинами d = 10 см. На расстоянии d1 = 4 см от пластины М помещают заземленную пластину Р (рис. 3-11, б). Найти изменение напряженности ΔЕ1 поля на участке МР и изменение напряженности поля ΔЕ2 на участке PN при этом. Построить графики зависимостей напряженностей Е = Е(х) и потенциала φ = φ(х) от расстояния между точками поля и пластинами.
Это конспект по теме «Потенциал. Разность потенциалов. ЗАДАЧИ с решениями». Выберите дальнейшие действия:
Понятие потенциала в физике
Что такое потенциал в физике? Это понятие очень часто применяется для описания качеств сил и полей самой разной природы. Скалярная функция, характеризующая некоторую величину, представляющуюся вектором, – вот что это потенциал. Гравитационный потенциал описывает соответствующее поле. В термодинамике это понятие применяется для системной внутренней энергии, в механике – для той или иной приложенной к предмету силы.
Электрика, прежде всего, интересует, что такое потенциал в электричестве. Из общего определения нетрудно вывести, что характеристика электрополя – это электрический потенциал. В своей статической форме электрический потенциал показывает потенциальную энергию одиночного «плюсового» заряда, помещаемого в данное место электрополя, и является одной из разновидностей электромагнитного потенциала. Вторая его форма – векторная (в отличие от скалярной), описывает магнитное поле.
Важно! Характеристика поля, описывающая зависимость работы при передвижении исключительно от исходной точки и места назначения, – это потенциальность поля. Траектория перемещения в этом случае на работу не влияет
Напряжение в цепях трёхфазного тока
В цепях трёхфазного тока различают фазное и линейное напряжения. Под фазным напряжением понимают среднеквадратичное значение напряжения на каждой из фаз нагрузки относительно нейтрали, а под линейным — напряжение между подводящими фазными проводами. При соединении нагрузки в фазное напряжение равно линейному, а при соединении в (при симметричной нагрузке или при глухозаземлённой нейтрали) линейное напряжение в 3<\displaystyle <\sqrt <3>>> раз больше фазного.
На практике напряжение трёхфазной сети обозначают дробью, в числителе которой стоит фазное при соединении в звезду (или, что то же самое, потенциал каждой из линий относительно земли), а в знаменателе — линейное напряжение. Так, в России наиболее распространены сети с напряжением 220/380 В; также иногда используются сети 127/220 В и 380/660 В.