Что называется компьютерной моделью
Компьютерное моделирование
Компьютерная модель (англ. computer model ), или численная модель (англ. computational model ) — компьютерная программа, работающая на отдельном компьютере, суперкомпьютере или множестве взаимодействующих компьютеров (вычислительных узлов), реализующая абстрактную модель некоторой системы. Компьютерные модели стали обычным инструментом математического моделирования и применяются в физике, астрофизике, механике, химии, биологии, экономике, социологии, метеорологии, других науках и прикладных задачах в различных областях радиоэлектроники, машиностроения, автомобилестроения и проч. Компьютерные модели используются для получения новых знаний о моделируемом объекте или для приближенной оценки поведения систем, слишком сложных для аналитического исследования.
Компьютерное моделирование является одним из эффективных методов изучения сложных систем. Компьютерные модели проще и удобнее исследовать в силу их возможности проводить т. н. вычислительные эксперименты, в тех случаях когда реальные эксперименты затруднены из-за финансовых или физических препятствий или могут дать непредсказуемый результат. Логичность и формализованность компьютерных моделей позволяет выявить основные факторы, определяющие свойства изучаемого объекта-оригинала (или целого класса объектов), в частности, исследовать отклик моделируемой физической системы на изменения ее параметров и начальных условий.
Построение компьютерной модели базируется на абстрагировании от конкретной природы явлений или изучаемого объекта-оригинала и состоит из двух этапов — сначала создание качественной, а затем и количественной модели. Компьютерное же моделирование заключается в проведении серии вычислительных экспериментов на компьютере, целью которых является анализ, интерпретация и сопоставление результатов моделирования с реальным поведением изучаемого объекта и, при необходимости, последующее уточнение модели и т. д.
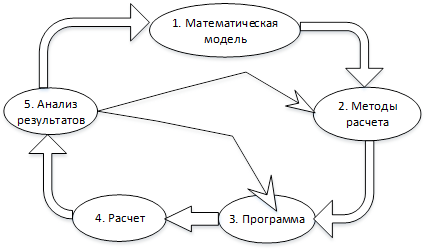
К основным этапам компьютерного моделирования относятся:
Различают аналитическое и имитационное моделирование. При аналитическом моделировании изучаются математические (абстрактные) модели реального объекта в виде алгебраических, дифференциальных и других уравнений, а также предусматривающих осуществление однозначной вычислительной процедуры, приводящей к их точному решению. При имитационном моделировании исследуются математические модели в виде алгоритма(ов), воспроизводящего функционирование исследуемой системы путем последовательного выполнения большого количества элементарных операций.
Содержание
Практическое применение
Компьютерное моделирование применяют для широкого круга задач, таких как:
Различные сферы применения компьютерных моделей предъявляют разные требования к надежности получаемых с их помощью результатов. Для моделирования зданий и деталей самолетов требуется высокая точность и степень достоверности, тогда как модели эволюции городов и социально-экономических систем используются для получения приближенных или качественных результатов.
Компьютерное моделирование
Что называется моделью? Для чего необходима модель? Какие бывают компьютерные модели? Что такое вычислительный эксперимент?
1. Модель и ее назначение
2. Классификация компьютерных моделей
Одним из эффективных способов изучения явлений является научный эксперимент, то есть воспроизведение изучаемого явления в контролируемых условиях, которыми можно управлять. Исследуемый объект часто заменяют компьютерной моделью ввиду большей удобности и экономичности. Благодаря распространению мощных ЭВМ и информационных технологий в настоящее время компьютерное моделирование можно назвать самым результативным методом исследования физических, технических и других систем. Компьютерные модели позволяют выявить основные условия, которые определяют свойства изучаемых явлений и объектов, изучить обратную связь системы на изменяющиеся условия.
Компьютерная модель – это отдельная программа либо программный комплекс, которые позволяют при помощи вычислений и графического отображения результатов воспроизводить реальные объекты и процессы при воздействии на них различных факторов. Такие модели еще называют имитационными.
Компьютерное моделирование – метод решения задачи анализа или синтеза сложной системы на основе изучения ее компьютерной модели. Смысл такого моделирования состоит в получении количественных и качественных результатов по созданной модели, что позволяет изучить неизвестные ранее свойства системы. Компьютерная модель должна отображать максимальное количество взаимосвязей и характеристик реального объекта, существующие ограничения. Модель следует строить универсальной, чтобы использовать ее для описания подобных объектов; простой, чтобы обойтись разумными тратами на исследование.
Компьютерная модель также является отличным наглядным и обучающим пособием для учащихся. При использовании компьютерной модели в качестве обучающего механизма существуют возможности:
Виды компьютерных моделей.
Для начала определимся, каким может быть компьютерное моделирование.
Исходя из всего вышеперечисленного, компьютерные модели можно разделить на:
Под компьютерным моделированием изначально подразумевалось только имитационное моделирование, однако, не трудно заметить, что использование компьютера для других целей может значительно помочь для решения поставленных задач. Например, построение современных математических моделей по входным экспериментальным данным невозможно или труднодостижимо без использования компьютера.
Первые задач, решаемые с помощью компьютерного моделирования, были связаны с физикой и представляли собой в основном сложные нелинейные задачи физики с помощью итерационных схем и по сути являлось математическим моделированием. Хорошие результаты в моделировании в области физики распространили использование этого метода исследования и на другие области. Сложность решаемых моделированием задач зависела только от мощности используемых компьютеров, тем самым и ограничивалась несовершенными мощностями
После публикации в 1948 году статьи Дж. Неймана и С. Улама, в которой впервые было описано применение метода Монте-Карло, многие исследователи стали называть компьютерное моделирование методами Монте-Карло. Это не верно, правильней будет выглядеть разделение компьютерного моделирования на несколько направлений[6]:
Разновидностью компьютерного моделирования является вычислительный эксперимент, который предполагает дальнейшее численное исследование модели после ее создания, позволяющее исследовать объект в различных его модификациях и при различных условиях.
3. Вычислительный эксперимент
С использованием ЭВМ для выполнения арифметических и логических операций производительность интеллектуального труда человека значительно возросла. Первые задачи, для которых создавались ЭВМ, были связаны с ядерной энергией и освоением пространства космоса. Сейчас же компьютер принимает участие в различных задачах и исследованиях, эта технология теоретических экспериментов получила название вычислительного эксперимента. Основой вычислительного эксперимента является математическое моделирование, теоретической базой – прикладная математика, а технической – мощные электронные вычислительные машины.
Компьютерное моделирование и вычислительный эксперимент становятся новым методом научного познания для исследования сложных моделей систем. Цикл вычислительного эксперимента принято разделять на несколько этапов для лучшего восприятия сути этого метода.
Цикл вычислительного эксперимента
Информатика. 11 класс
Конспект урока
Информатика, 11 класс. Урок № 9.
Тема — Компьютерное моделирование
Любое явление или объект обладает огромным количеством свойств, характеристик или параметров, охватить которые бывает очень сложно, поэтому приходится проводить упрощение такого объекта, отбрасывая несущественные детали. Иными словами, строить модель.
Под моделью мы будем понимать любой материальный или идеальный объект, обладающий некоторыми свойствами, совпадающими со свойствами реального объекта.
При этом исследователь будет выбирать такие свойства, которые являются существенными для изучаемого объекта. Например, при проектировке здания архитектору важен внешний вид объекта, для инженера — прочность и материалы, для инженера-геолога – нагрузка на грунт. Поэтому модель одного и того же здания будет различна.
Давайте рассмотрим еще один класс моделей — это математические модели. Например, все геометрические объекты (круг, треугольник, прямая) являются моделями. В окружающем нас мире не существует таких объектов.
Например, стол. Можем ли мы сказать, что он идеально прямоугольный? Нет, конечно, так как каждый край стола не может быть идеальной прямой линией. Однако, во многих случаях можно считать, что это так.
Подобные рассуждения справедливы и для всех других математических объектов — вектор, числа, функций, производных, интегралов.
Будем считать, что математическое моделирование — это описание реальной ситуации с помощью математических терминов, математических операций и математической символики.
Основоположником математического моделирования в России был академик Российской академии наук Александр Андреевич Самарский, который первый предложил использовать математические модели, реализуемые с помощью компьютера и дальнейшее их исследование. Важнейшим преимуществом использования таких моделей заключается в невысоких финансовых затратах и относительной простоте. При этом практика является и остается критерием истинности и завершающим звеном в исследовании.
Моделирование требует четкого плана действий. На первом этапе формируется задача, которую необходимо решить с помощью модели, далее разрабатывается некий математический эквивалент исследуемого объекта, после чего происходит тестирование такой модели и сравнение с практическими знаниями. Если модель на тестовом этапе не противоречит практике, то проводится эксперимент с моделью, после чего анализируются результаты и делаются выводы. Давайте рассмотрим все этапы моделирования на примере колеса, вращающегося внутри более большого:
ЭТАП 1. Постановка задачи
В колесе радиуса R катится колесо радиуса r. Какую траекторию описывает точка, расположенная на ободе колеса r?
ЭТАП 2. Математическая модель
Траектория движения этой точки находится по формулам:
где φ изменяется от 0 до 2π (угол смещения колеса r).
ЭТАП 3. Алгоритм решения
Для получения траектории движения колеса, нам необходимо изменять значение φ от 0 до 30. Вычислять координаты и представлять их на графике. Попробуем это сделать с помощью программы Excel.
ЭТАП 4. Разработка программы. Тестирование
Создадим таблицу по образцу:
В столбец А занесем значения угла φ от 0 до 6.28 с шагом 0.01.
Запишем в ячейку 
С помощью маркера заполнения распространим эти формулы до конца таблицы.
По значениям столбцов B и С построим точечный график:
*Если Excel выдает ошибку «#ДЕЛ/0» — введите в ячейки F3 и F4 значения.
ЭТАП 5. Вычислительный эксперимент
Изменяя значения в ячейках F3 и F4, получи различные картинки:
ЭТАП 6. Анализ результатов. Выводы
Вычислительный эксперимент показал, что вид фигуры зависит от отношения радиусов маленького и большого колеса. Такие фигуры носят названия — ГИПОЦИКЛЫ.
Попробуйте самостоятельно получить следующие фигуры:
Компьютерное моделирование



Компьютерная модель (англ. computer model), или численная модель – компьютерная программа, работающая на отдельном компьютере или множестве взаимодействующих компьютеров (вычислительных узлов), реализующая абстрактную модель некоторой системы.
Компьютерное моделирование – метод решения задачи анализа или синтеза сложной системы на основе использования ее компьютерной модели.
Для поддержки математического моделирования разработаны системы компьютерной математики, например, Maple, Mathematica, Mathcad, MATLAB, VisSim и др. Они позволяют создавать формальные и блочные модели как простых, так и сложных процессов и устройств и легко менять параметры моделей в ходе моделирования. Блочные модели представлены блоками (чаще всего графическими), набор и соединение которых задаются диаграммой модели.
Дискретная модель – математическая модель, которая описывает поведение и свойства объекта только в отдельные моменты времени.
Модель лабиринтного поиска – поиск оптимального пути от входных данных к результату.
Эвристическое моделирование заключается в стремлении воспроизвести то, что однажды уже привело к успеху.
Компьютерные модели стали обычным инструментом математического моделирования и применяются в физике, астрофизике, механике, химии, биологии, экономике, социологии, метеорологии, других науках и прикладных задачах в различных областях радиоэлектроники, машиностроения, автомобилестроения и проч. Компьютерные модели используются для получения новых знаний о моделируемом объекте или для приближенной оценки поведения систем, слишком сложных для аналитического исследования.
Компьютерное моделирование является одним из эффективных методов изучения сложных систем. Компьютерные модели проще и удобнее исследовать в силу их возможности проводить вычислительные эксперименты в тех случаях, когда реальные эксперименты затруднены из-за финансовых или физических препятствий или могут дать непредсказуемый результат. Логичность и формализованность компьютерных моделей позволяет выявить основные факторы, определяющие свойства изучаемого объекта-оригинала (или целого класса объектов), в частности, исследовать отклик моделируемой физической системы на изменения ее параметров и начальных условий.
Построение компьютерной модели базируется на абстрагировании от конкретной природы явлений или изучаемого объекта-оригинала и состоит из двух этапов: сначала создание качественной, а затем и количественной модели. Компьютерное же моделирование заключается в проведении серии вычислительных экспериментов на компьютере, целью которых является анализ, интерпретация и сопоставление результатов моделирования с реальным поведением изучаемого объекта и, при необходимости, последующее уточнение модели и т.д.
К основным этапам компьютерного моделирования относятся:
1. Постановка задачи, определение объекта моделирования.
2. Разработка концептуальной модели, выявление основных элементов системы и их взаимосвязей.
3. Формализация, то есть переход к математической модели.
4. Создание алгоритма и написание программы.
5. Планирование и проведение компьютерных экспериментов.
6. Анализ и интерпретация результатов.
Различают аналитическое и имитационное моделирование.
При аналитическом моделировании изучаются математические (абстрактные) модели реального объекта в виде алгебраических, дифференциальных и других уравнений, а также предусматривающих осуществление однозначной вычислительной процедуры, приводящей к их точному решению.
При имитационном моделировании исследуются математические модели в виде алгоритма, воспроизводящего функционирование исследуемой системы путем последовательного выполнения большого количества элементарных операций.
Компьютерное моделирование применяют для широкого круга задач, таких как:
Моделирование ядерных испытаний.
Моделирование радиационного воздействия на организм человека.
Анализ распространения загрязняющих веществ в атмосфере.
Конструирование транспортных средств.
Полетные имитаторы для тренировки пилотов.
Прогнозирование цен на финансовых рынках.
Исследование поведения зданий, конструкций и деталей под механической нагрузкой.
Прогнозирование прочности конструкций и механизмов их разрушения.
Проектирование производственных процессов, например химических.
Стратегическое управление организацией.
Исследование поведения гидравлических систем: нефтепроводов, водопровода.
Моделирование сценарных вариантов развития городов.
Моделирование транспортных систем.
Различные сферы применения компьютерных моделей предъявляют разные требования к надежности получаемых с их помощью результатов. Для моделирования зданий и деталей самолетов требуется высокая точность и степень достоверности, тогда как модели эволюции городов и социально-экономических систем используются для получения приближенных или качественных результатов.
Компьютерные модели
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику

Государственное бюджетное образовательное учреждение
среднего профессионального образования Свердловской области
«Слободотуринский аграрно – экономический техникум»
Выполнили: студенты гр.113ПК
с. Туринская Слобода
Содержание
Введение
Важнейшим условием информатизации общества, подготовки человека к полноценной жизни в условиях современного общества является информатизация образования. Без прочного фундамента, заложенного в сфере образования, никакие, даже самые выдающиеся научные открытия, не сделают наше общество действительно информационным.
В нашем образовательном учреждении успешно применяются информационные технологии, как на уроках общеобразовательных дисциплин, так и на уроках специальных дисциплин. С помощью компьютера преподаватели демонстрируют информацию используя разное программное обеспечение.
странички интернет ресурсов;
Создавать текстовые документы, электронные таблицы, презентации, рисунки, фотографии и видео ролики мы можем.
А как создаются компьютерные модели? Это видео или рисунки, анимация или презентация. Сможем ли мы создать компьютерную модель не применяя специальных программ анимации, дизайна, 3 D моделирования. Используя только инструментальную программу Паскаль.
Гипотеза. Если мы изучим основные аспекты построения компьютерной модели, то скорее всего мы сможем реализовать не сложный алгоритм в инструментальной программе Паскаль, то есть построить компьютерную модель.
Цель проекта построить компьютерную модель физического явления с помощью инструментальной программы Паскаль.
Для достижения цели нам необходима решить следующие задачи:
изучить принцип анимационных моделей;
построить экспериментальную модель;
построить модель физического явления.
Основная часть
Моделирование и его виды
Моделирование является одним из способов познания мира.
Понятие моделирования достаточно сложное, оно включает в себя огромное разнообразие способов моделирования: от создания натуральных моделей (уменьшенных и или увеличенных копий реальных объектов) до вывода математических формул.
Для различных явлений и процессов бывают уместными разные способы моделирования с целью исследования и познания.
Объект, который получается в результате моделирования, называется моделью. Должно быть понятно, что это совсем не обязательно реальный объект. Это может быть математическая формула, графическое представление и т.п. Однако он вполне может заменить оригинал при его изучении и описании поведения.
Хотя модель и может быть точной копией оригинала, но чаще всего в моделях воссоздаются какие-нибудь важные для данного исследования элементы, а остальными пренебрегают. Это упрощает модель. Но с другой стороны, создать модель – точную копию оригинала – бывает абсолютно нереальной задачей. Например, если моделируется поведение объекта в условиях космоса. Можно сказать, что модель – это определенный способ описания реального мира.
Моделирование проходит три этапа:
Применение результатов исследования на практике и/или формулирование теоретических выводов.
Видов моделирования огромное количество. Вот некоторые примеры типов моделей:
Математические модели. Это знаковые модели, описывающие определенные числовые соотношения.
Графические модели. Визуальное представление объектов, которые настолько сложны, что их описание иными способами не дает человеку ясного понимания. Здесь наглядность модели выходит на первый план.
Имитационные модели. Позволяют наблюдать изменение поведения элементов системы-модели, проводить эксперименты, изменяя некоторые параметры модели.
Над созданием модели могут работать специалисты из разных областей, т.к. в моделировании достаточно велика роль межпредметных связей.
Особенности компьютерного моделирования
Совершенствование вычислительной техники и широкое распространение персональных компьютеров открыло перед моделированием огромные перспективы для исследования процессов и явлений окружающего мира, включая сюда и человеческое общество.
Компьютерное моделирование – это в определенной степени, то же самое, описанное выше моделирование, но реализуемое с помощью компьютерной техники.
Для компьютерного моделирования важно наличие определенного программного обеспечения.
При этом программное обеспечение, средствами которого может осуществляться компьютерное моделирование, может быть как достаточно универсальным (например, обычные текстовые и графические процессоры), так и весьма специализированными, предназначенными лишь для определенного вида моделирования.
Очень часто компьютеры используются для математического моделирования. Здесь их роль неоценима в выполнении численных операций, в то время как анализ задачи обычно ложится на плечи человека.
Обычно в компьютерном моделировании различные виды моделирования дополняют друг друга. Так, если математическая формула очень сложна, что не дает явного представления об описываемых ею процессах, то на помощь приходят графические и имитационные модели. Компьютерная визуализация может быть намного дешевле реального создания натуральных моделей.
С появлением мощных компьютеров распространилось графическое моделирование на основе инженерных систем для создания чертежей, схем, графиков.
Если система сложна, а требуется проследить за каждым ее элементом, то на помощь могут придти компьютерные имитационные модели. На компьютере можно воспроизвести последовательность временных событий, а потом обработать большой объем информации.
Однако следует четко понимать, что компьютер является хорошим инструментом для создания и исследования моделей, но он их не придумывает. Абстрактный анализ окружающего мира с целью воссоздания его в модели выполняет человек.
Экспериментальная модель
Прежде чем приступить к построению компьютерной модели нам необходимо изучить технологию движения объектов в инструментальной программе Паскаль.
Паскаль ( англ. Pascal) — язык программирования общего назначения. Один из наиболее известных языков программирования, используется для обучения программированию в старших классах и на первых курсах вузов, является базой для ряда других языков
Нарисуем объект (рис.1). Для этого в программе Паскаль напишем текст программы:
Основа движения- это повторяющееся объекты, поэтому изменим программу, чтобы объекты повторялись (рис.2).
Рисунок Объект повторения
Круги появляются постепенно, если закрашивать предыдущие, то появляется эффект движения (рис.3).
Дополним текст программы:
Рисунок Объект движения
В компьютерной модели предполагается движение по окружности, для этого мы изучили построение основных математических функций синус, косинус и др. И наложили движение объекта на график математической функции (рис.4). В этом случае программа существенно усложнилась.
(полный текст программы представлен в приложении 1.)
for x_ekr:=0 to 799 do
Рисунок Функция синус
Изучив и применив полученные теоретические знания в экспериментальной модели построение объекта, движение объекта, движение объекта по графику математической функции мы можем приступить к построению компьютерной модели.
Компьютерная модель атома
Приступим к созданию модели атома. Рассмотрим существующие модели: ядро атома, обычно располагается в центре модели; электрон как правило движущийся объект, двигается по стационарной орбите вокруг ядра.
Такую не сложную модель атома возможно реализовать с помощью инструментальной программы Паскаль.
Сначала создадим изображение атома. Напишем алгоритм программы на языке программирования Паскаль (рис.5).
(полный текст программы представлен в приложении 2.)
Чтобы будущая модель имела более эффектный вид, из окружности сделаем эллипс, то получится эффект объемной модели. Дополним программу коэффициентом сжатия окружности (рис.6).
Заменим строчку circle ( cx +100, cy , Re ); на строчку Ellipse ( cx -100, cy -40, cx +100, cy +40); (полный текст программы представлен в приложении 3.)
Рисунок Атом в объёме
Придадим движение электрону по намеченной орбите, для этого дополним программу циклом повторения изображения электрона с точкой, точка обозначает орбиту вместо линии (рис.7).);
(полный текст программы представлен в приложении 4).
x:=round((Ra-Dr)*cos(I))+cx; y:=round(k*(Ra-Dr)*sin(i))+cy; <определить координаты электронов >
Рисунок Компьютерная модель атома
Данная модель может считаться простейшей компьютерной моделью атома.
Дополним модель электронами с разными орбитами и разной степенью сжатия орбиты (рис.8)).
(полный текст программы представлен в приложении 5).
Рисунок Компьютерная модель атома Гелий
Заключение
Компьютерное моделирование физических процессов является не только интересным направлением программирования, но и имеет большое практическое значение не только в учебном процессе, но и в других сферах производственной и экономической деятельности человека. И наверное будет актуальным еще долгое-долгое время.
В результате выполнения практического проекта мы полностью достигли заявленной цели: построили компьютерную модель физического явления с помощью инструментальной программы Паскаль. – мы построили компьютерную модель атома. Данную модель атома можно демонстрировать на уроках физики, химии, как в нашем образовательном учреждении, так и в школе.
К сожалению программа Паскаль ограничена набором визуальных эффектов, не предоставляет возможности в полной мере передать красоту нашего мира, ограничена палитра красок (всего 16 цветов), отсутствует 3 D представление но и другие эффекты.
В дальнейшем мы планируем продолжить изучение данного направления, но с использованием специального программного обеспечения.
Литература
Л.Н. Бахвалов «Компьютерное моделирование», М., «МЦНМО», 2009;
А.В. Немухин «Компьютерное моделирование в нашей жизни», М, 2005;
Приложение 1
Текст программы движения объекта
по графику математической функции y = sin x