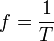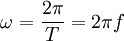Что называется колебанием классификация колебаний
Колебания и их классификация
Колебания – разнообразные движения и процессы, имеющие определенную повторяемость во времени. Для определения колебаний необходимо знать зависимость параметра колебаний от времени.
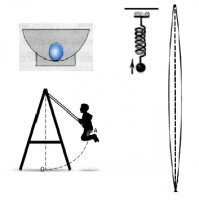
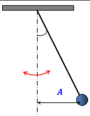
1. Колебания маятника в зависимости от угла его отклонения относительно вертикального положения
2. Изгибные колебания балки
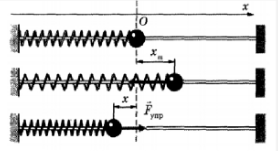
3. Колебания груза на пружине
В зависимости от внешнего вида и причин возникновения различают следующие виды колебаний:
1. Детерминированные, случайные, хаотические;
2. Затухающие, стационарные, нарастающие (по виду графика);
3. Собственные, вынужденные, параметрические (по характеру внешнего воздействия).
Детерминированные колебания описываются функцией времени в форме аналитического выражения или графика, что позволяет определить его параметры в любой момент времени.
Рис 1. Детерминированные колебания
Детерминированные колебания могут носить периодический характер с периодом повторения Т или быть представлены в форме одиночного, непериодического колебания, рис 1, д.
Периодические колебания на интервале времени 

где 

Периодические колебания разделяются на:
— полигармонические (рис 1, б)
— релаксационные, в которых сравнительно медленные изменения состояния системы чередуется с быстрыми(скачкообразными). рис 1,в.
— импульсные колебания характеризуются наличием пауз между колебаниями, рис 1, г.
— затухающие колебания – колебания, амплитуда которых при t → ∞ стремится к нулю. Затухающие колебания описываются функцией.

— нарастающие колебания – амплитуда 


— стационарные колебания – колебания, амплитуда f,начиная с некоторого момента, постоянна:

Случайные колебания – колебания, в которых один или несколько параметров случайно зависят от времени и поэтому их относят к классу случайных процессов, рис. 2.а.
Рис. 2. Случайные колебания
Хаотические колебания являются промежуточными между детерминированными и случайными. Природа их сложна. Часто хаотические колебания состоят из фрагментов почти периодических колебаний с различными периодами колебаний рис. 2,б. Хаотические колебания могут возникать из периодических автоколебаний под действием внешнего гармонического воздействия, либо зарождаться в самой системе при воздействии ее элементов.
Собственные колебания – колебания, происходящие в объекте, после устранения внешнего воздействия. Как правило, это затухающие колебания вследствие наличия трения в любой колебательной системе.
Вынужденные колебания – колебания, возникающие в объекте под действием внешнего воздействия. Причем в объекте одновременно присутствуют вынужденные и свободные колебания. Со временем свободные колебания затухают, а вынужденные остаются.
Параметрические колебания – возникают, когда энергия объекту передается посредством периодического изменения какого-либо из ее параметров. Процесс возникновения параметрических колебаний параметрическим возбуждением. Например, качели, раскачиваются изменением центра тяжести.
Автоколебания – колебания, возникающие и поддерживаемые без приложения внешнего воздействия. Компенсация потерь осуществляется за счет отбора энергии из колебательной системы, а после ее увеличения происходит возврат в тот же самый объект при определенных условиях.
В зависимости от компенсирующих устройств и свойств объекта автоколебания могут быть гармоническими, полигармоническими, релаксационными, импульсными, или хаотическими.
Колебания
Колеба́ния — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку.
Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму.
Колебания различной физической природы имеют много общих закономерностей и тесно взаимосвязаны c волнами. Поэтому исследованиями этих закономерностей занимается обобщённая теория колебаний и волн. Принципиальное отличие от волн: при колебаниях не происходит переноса энергии, это, так сказать, «местные» преобразования энергии.
Содержание
Классификация
Выделение разных видов колебаний зависит от подчёркиваемых свойств колеблющихся систем (осцилляторов)
По физической природе
По характеру взаимодействия с окружающей средой
Характеристики
Период колебаний 


В круговых или циклических процессах вместо характеристики «частота» используется понятие круговая (циклическая) частота 

См. также
Литература
| Геометрическая оптика • Физическая оптика • Волновая оптика • Квантовая оптика • Нелинейная оптика • Теория испускания света • Теория взаимодействия света с веществом • Спектроскопия • Лазерная оптика • Фотометрия • Физиологическая оптика • Оптоэлектроника • Оптические приборы | |
| Смежные направления | Акустооптика • Кристаллооптика |
|---|---|
| Общая (физическая) акустика • Геометрическая акустика • Психоакустика • Биоакустика • Электроакустика • Гидроакустика • Ультразвуковая акустика • Квантовая акустика (акустоэлектроника) • Акустическая фонетика (Акустика речи) | |
| Прикладная акустика | Архитектурная акустика (Строительная акустика) • Аэроакустика • Музыкальная акустика • Акустика транспорта • Медицинская акустика • Цифровая акустика |
|---|---|
| Смежные направления | Акустооптика |
Полезное
Смотреть что такое «Колебания» в других словарях:
КОЛЕБАНИЯ — движения (изменения состояния), обладающие той или иной степенью повторяемости. Наиболее распространены:1) механические колебания: колебания маятника, моста, корабля на волне, струны, колебания плотности и давления воздуха при распространении… … Большой Энциклопедический словарь
КОЛЕБАНИЯ — КОЛЕБАНИЯ, процессы (в наиболее общем смысле), периодически меняющие свое направление со временем. Процессы эти могут быть весьма разнообразными. Если напр. подвесить на стальной спиральной пружине тяжелый шар, оттянуть его и затем предоставить… … Большая медицинская энциклопедия
колебания — Движения или процессы, обладающие той или иной степенью повторяемости во времени [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] колебания Элемент временного ряда, отражающий происходящие в экономике периодические … Справочник технического переводчика
Колебания — [oscillation] элемент временного ряда, отражающий происходящие в экономике периодические изменения, например, подъемы и спады производства продукции и потребления тех или иных товаров. В экономико математических моделях для приближенного… … Экономико-математический словарь
КОЛЕБАНИЯ — (Oscillations) в самом общем смысле всякий периодический (повторяющийся) процесс, напр. периодическое движение точки под влиянием силы, притягивающей ее к положению равновесия (механические К.), или периодическое изменение электромагнитного поля… … Морской словарь
КОЛЕБАНИЯ — движения или процессы, обладающие той или иной степенью повторяемости во времени. В зависимости от природы процесса различают К.: механические, электрические (тока и напряжения), звуковые, электромеханические. Все они могут быть периодическими,… … Большая политехническая энциклопедия
колебания — движения (изменения состояния), обладающие той или иной степенью повторяемости. Наиболее распространены: 1) механические колебания: колебания маятника, моста, корабля на волне, струны, колебания плотности и давления воздуха при распространении… … Энциклопедический словарь
Колебания — движения (изменения состояния), обладающие той или иной степенью повторяемости. При К. маятника повторяются отклонения его в ту и другую сторону от вертикального положения. При К. пружинного маятника груза, висящего на пружине,… … Большая советская энциклопедия
КОЛЕБАНИЯ — движения (изменения состояния), характеризующиеся той или иной степенью повторяемости во времени. К. могут иметь разл. физ. природу, а также отличаться механизмом возбуждения, характером, степенью повторяемости и быстротой смены состояний (см.… … Большой энциклопедический политехнический словарь
Колебание
Колеба́ния — повторяющийся в той или иной степени во времени процесс изменения состояний системы. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку.
Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму.
Колебания различной физической природы имеют много общих закономерностей и тесно взаимосвязаны c волнами. Поэтому исследованиями этих закономерностей занимается обобщённая теория колебаний и волн. Принципиальное отличие от волн: при колебаниях не происходит переноса энергии, это, так сказать, «местные» преобразования энергии.
Содержание
Классификации колебаний
Выделение разных видов колебаний зависит от свойства, которое хотят подчеркнуть.
Для подчёркивания разной физической природы колеблющихся систем (осцилляторов) выделяют, например, колебания:
По характеру взаимодействия с окружающей средой:
Характеристики колебаний
Амплитуда 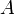
Промежуток времени 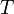
Период колебаний 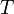
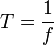
См. также
Литература
Полезное
Смотреть что такое «Колебание» в других словарях:
колебание — См. сомнение … Словарь синонимов
КОЛЕБАНИЕ — КОЛЕБАНИЕ, колебания, ср. (книжн.). 1. Действие по гл. колебаться. Колебание струны. Колебания маятника. 2. перен. Нерешительность, неустойчивость, сомненье. После долгих колебаний я решился уехать в провинцию. || Неустойчивость, частое изменение … Толковый словарь Ушакова
колебание — КОЛЕБАТЬСЯ, леблюсь, леблешься; леблясь; несов. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
колебание — Движение (изменение состояния), характеризующееся той или иной степенью повторяемости во времени. [Система неразрушающего контроля. Виды (методы) и технология неразрушающего контроля. Термины и определения (справочное пособие). Москва 2003 г.]… … Справочник технического переводчика
Колебание — – движение (изменение состояния), характеризующееся той или иной степенью повторяемости во времени. [Система неразрушающего контроля. Виды (методы) и технология неразрушающего контроля. Термины и определения (справочное пособие). Москва… … Энциклопедия терминов, определений и пояснений строительных материалов
колебание — • значительное колебание • резкое колебание • сильное колебание … Словарь русской идиоматики
колебание — ▲ отклонение ↑ обратимый колебание обратимое отклонение. колебания отклонения в обе стороны от среднего положения (# спроса. # погоды. совершать #). ▼ ФИЗИЧЕСКИЕ КОЛЕБАНИЯ см. посредством, чередование в направлении, п … Идеографический словарь русского языка
колебание — rus вибрация (ж), колебание (с) eng vibration fra vibration (f) deu Schwingung (f), Vibration (f) spa vibración (f) … Безопасность и гигиена труда. Перевод на английский, французский, немецкий, испанский языки
КОЛЕБАНИЕ — (swing) см. Электоральное колебание … Большой толковый социологический словарь
колебание — svyravimas statusas T sritis automatika atitikmenys: angl. oscillation vok. Schwankung, f; Schwingen, n; Schwingung, f rus. колебание, n pranc. oscillation, f … Automatikos terminų žodynas
Механические колебания
теория по физике 🧲 колебания и волны
Колебательное движение очень распространено. Заставить колебаться можно любое тело, если приложить к нему силу — однократно или постоянно. К примеру, если подтолкнуть качели, они начнут качаться вперед-назад, и такое движение будет приблизительно повторяться до тех пор, пока качели полностью не остановятся.
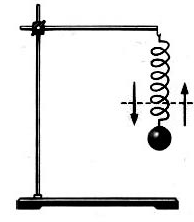
Другой пример колебательного движения — тело, подвешенное к пружине. Если его потянуть вниз и отпустить, то за счет сил упругости оно сначала поднимется вверх, а затем снова опустится вниз, затем движения вверх-вниз будут повторяться. Со временем они прекратятся под действием силы сопротивления воздуха.
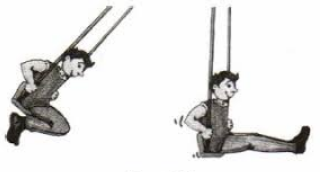
Колебаниями можно назвать даже движение гири, которую поднимается тяжелоатлет вверх, а затем опускает в низ. При этом он будет прикладывать к гире силу постоянно. Гиря будет колебаться до тех пор, пока к нему будет прикладываться эта сила.
Колебания — это движения, которые точно или приблизительно повторяются через определенные интервалы времени.
Механические колебания — это колебательные движения, совершаемые физическим телом в механической системе.
Механическая система — совокупность материальных точек (тел), движения которых взаимосвязаны между собой.
Какими бывают колебания?
Напомним, что в механической системе выделяют два вида сил:
Свободные колебания
Свободные колебания — колебания, происходящие в системе под действием внутренних сил после того, как эта система выведена из положения равновесия.
Колебательная система — механическая система, в которой возможно совершение свободных колебаний.
Свободные колебания в колебательной системе могут возникнуть только при наличии двух условий:
Примеры свободных колебаний:
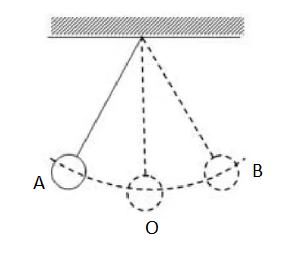
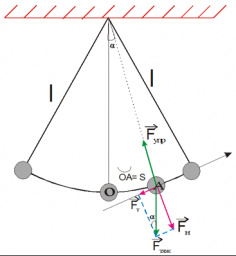
Примером колебательной системы также служит математический маятник — материальная точка, подвешенная на невесомой нерастяжимой нити. В действительности такого маятника не существует. Это идеализированная модель реального маятника, примером которого служит тяжелый шарик, подвешенный на длинной нити. В этом случае размером шарика и растяжением нити можно пренебречь.
В колебательную систему математического маятника входят:
В положении равновесия (точка О) шарик висит на нити и покоится. Если его отклонить от положения равновесия до точки А и отпустить, под действием силы тяжести шарик приблизится к положению равновесия. Так как к этому моменту шарик обретет скорость, он не сможет остановиться и приблизится к точке В. Затем он снова вернется в точку А через положение равновесия в точке О. Шарик будет колебаться, пока не затухнут под действием возникающей силы сопротивления воздуха.
Вынужденные колебания
Вынужденные колебания — колебания тел под действием внешних периодически изменяющихся сил.
Примерами вынужденных колебаний служат:
Затухающие и незатухающие колебания
Затухающие колебания — колебания, которые со временем затухают. При этом максимальное отклонение тела от положения равновесия с течением времени уменьшается.
Колебания затухают под действием сил, препятствующих колебательному движению. Так, шарик в сферической чаше перестает колебаться под действием силы трения. Математический маятник и качели перестают совершать колебательные движения за счет силы сопротивления воздуха.
Все свободные колебания являются затухающими, так как всегда присутствует трение или сопротивление среды.
Незатухающими колебаниями могут быть только те, которые совершаются под действием периодической внешней силы (вынужденные колебания). Так, ветка будет раскачиваться до тех пор, пока дует ветер. Когда он перестанет дуть, колебания ветки со временем затухнут. Иголка швейной машинки будет совершать колебательные движения до тех пор, пока швея вращает ручку привода. Когда она перестанет это делать, иголка сразу остановится.
Динамика колебательного движения
Для того чтобы описать количественно колебания тела пол действием силы упругости пружины или колебания шарика, подвешенного на нити, воспользуемся законами механики Ньютона.
Уравнение движения тела, колеблющегося под действием сил упругости
Рассмотрим колебательное движение шарика, вызванное силой упругости, возникшей при растяжении горизонтальной пружины вдоль оси Ох.
Согласно II закону Ньютона произведение массы тела на ускорение равно равнодействующей всех сил приложенных к телу. Поскольку сила трения пренебрежимо мала, мы можем считать, что в этой механической системе действует единственная сила — сила упругости. Учтем, что шарик колеблется вдоль одной прямой, и выберем одномерную систему координат Ох. Тогда:
Согласно закону Гука, проекция сила упругости прямо пропорциональная смещению шарика из положения равновесия (точки О). Смещение равно координате x шарика, причем проекция силы и координаты имеют разные знаки. Это связано с тем, что сила упругости всегда направлена к точке равновесия, в то время как расстояние от этой точки во время движения увеличивается в обратную сторону. Отсюда делаем вывод, что сила упругости равна:
где k — жесткость пружины.
Тогда уравнение движения шарики принимает вид:
Пример №1. Груз массой 0,1 кг прикрепили к пружине школьного динамометра жесткостью 40 Н/м. В начальный момент времени пружина не деформирована. После того, как груз отпускают, возникают колебания. Чему равна максимальная скорость груза?
Максимальной скорости груз достигнет при максимальном его отклонении от положения равновесия — в нижней точке траектории. Учтем, что тело движется вниз под действием силы тяжести. Но в то же время на него действует сила упругости, которая возникает в пружине и нарастает до тех пор, пока не становится равной по модулю силе тяжести. Применив III закон Ньютона получим:
∣ ∣ ∣ → F т я ж ∣ ∣ ∣ = ∣ ∣ ∣ → F у п р ∣ ∣ ∣
где y m a x — максимальное отклонение груза от положения равновесия. В этой точке скорость тела будет максимальная. Для нахождения этой величины используем формулу из кинематики:
Начальная скорость равна нулю. Отсюда:
Максимальная скорость равна:
Уравнение движения математического маятника
Ниже на рисунке представлен математический маятник. Если мы выведем из положения равновесия шарик и отпустим, возникнет две силы:
При колебаниях шарика также будет возникать сила сопротивления воздуха. Но так как она очень мала, мы будем ею пренебрегать.
Чтобы описать динамику движения математического маятника, удобно силу тяжести разложить на две составляющие:
Причем компонента → F τ направлена перпендикулярно нити, а → F n — вдоль нее.
Компонента → F τ представляет собой проекцию силы тяжести в момент, когда нить маятника отклонена от положения равновесия (точки О) на угол α. Следовательно, она равна:
Знак «–» мы здесь поставили по той причине, что компоненты силы тяжести → F τ и α имеют противоположные знаки. Ведь если отклонить шарик на угол α>0, то составляющая → F τ будет направлена в противоположную сторону, так как она будет пытаться вернуть шарик в положение равновесия. И ее проекция будет отрицательной. Если же шарик отклонить на угол α → F τ будет направлена в обратную сторону. В этом случае ее проекция будет положительной.
Разделим обе части выражения на массу шарика m и получим:
Внимание! Чтобы перевести градусы в радианы, нужно умножить градусы на число π и поделить результат на 180. К примеру 2 о = 2∙3,14/180 рад., или 2 о = 0,035 рад.
При малом отклонении также дугу ОА мы можем принять за длину отрезка OA, который мы примем за s. Тогда угол α будет равен отношению противолежащего катета (отрезка s) к гипотенузе (длине нити l):
Это уравнение похоже на то уравнение, которое мы получили для описания колебательного движения шарика под действием силы упругости. И оно также позволяет сделать вывод, что ускорение прямо пропорционально координате.
При отклонениях на малый угол мы можем пользоваться следующей формулой:
Чтобы найти длину нити, нужно выразить угол α в радианах:
Тогда длина нити равна:
Основные характеристики колебательного движения
Амплитуда — максимальное отклонение тела от положения равновесия. Обозначается буквой A, иногда — xmax. Единиц измерения — метр (м).
Период — время совершения одного полного колебания. Обозначается буквой T. Единица измерения — секунда (с).
Период и частота колебаний связаны между собой следующей формулой:
Период колебаний также можно вычислить, зная количество совершенных колебаний N за время t:
Поскольку частота — это величина, обратная периоду колебаний, ее можно выразить в виде:
Пример №3. Определить частоту колебаний груза, если суммарный путь, который он прошел за 2 секунды под действием силы упругости, составил 1 м. Амплитуда колебаний равна 10 см.
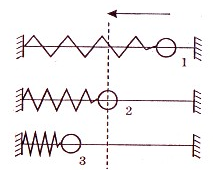
Во время одного колебания груз проходит расстояние, равное 4 амплитудам. Посмотрите на рисунок. Положение равновесия соответствует состояние 2. Чтобы совершить одно полное колебание, сначала груз отводят в положение 1. Когда его отпускают, он проходит путь 1–2 и достигает положения равновесия. Этот путь равен амплитуде колебаний. Затем он продолжает движение до состояния 3. И в это время он проходит расстояние 2–3, равное еще одной амплитуде колебаний. Чтобы вернуться в исходное положение (состояние 1), нужно снова проделать путь в обратном направлении: сначала 3–2, затем 2–1.
Следовательно, количество колебаний равно отношению пройденного пути к амплитуде, помноженной на 4:
Так как мы знаем, что эти колебания совершались в течение 2 секунд, для вычисления частоты мы можем использовать формулу:
В таблице представлены данные о положении шарика, колеблющегося вдоль оси Ох, в различные моменты времени.
Каков период колебаний шарика?
Алгоритм решения
Решение
Из таблицы видно, что амплитуда колебаний равна 15 мм. Следовательно, максимальное отклонение в противоположную сторону составляет –15 мм. Расстояние между двумя максимальными отклонениями от положения равновесия шарика равно половине периода колебаний. Этим значения в таблице соответствует время 1 и 3 секунды соответственно. Следовательно, разница между ними — половина периода. Тогда период будет равен удвоенной разнице во времени:
T = 2 ( t 2 − t 1 ) = 2 ( 3 − 1 ) = 4 ( с )
pазбирался: Алиса Никитина | обсудить разбор | оценить
Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания. Пружина всё время остается растянутой. Как ведут себя потенциальная энергия пружины, кинетическая энергия груза, его потенциальная энергия в поле тяжести, когда груз движется вверх к положению равновесия?
Для каждой величины определите соответствующий характер изменения:
| 1) | увеличивается |
| 2) | уменьшается |
| 3) | не изменяется |
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
Решение
Потенциальная энергия пружины определяется формулой:
где k — коэффициент жесткости пружины, а x — ее удлинение. Величина x была максимальной в нижней точке траектории. Когда пружина начинает сжиматься, она уменьшается. Так как потенциальная энергия зависит от квадрата x прямо пропорционально, то при уменьшении этой величины потенциальная энергия пружины тоже уменьшается.
Кинетическая энергия тела определяется формулой:
В нижней точке траектории скорость шарика была равна нулю. Но к этому времени потенциальная энергия пружины достигла максимума. Она начинает с ускорением поднимать шарик вверх, сжимаясь. Следовательно, скорость растет. Так как кинетическая энергия зависит от квадрата скорости тела прямо пропорционально, то при увеличении скорости этой величины кинетическая энергия шарика тоже увеличивается.
Потенциальная энергия тел в поле тяжести земли определяется формулой:
Масса и ускорение свободного падения шарика — постоянные величины. Следовательно, потенциальная энергия зависит только от расстояния до поверхности земли. Когда пружина поднимает шарик, расстояние между ним и землей увеличивается. Так как потенциальная энергия зависит от расстояния прямо пропорционально, то при его увеличении потенциальная энергия шарика тоже растет.
pазбирался: Алиса Никитина | обсудить разбор | оценить
В таблице представлены данные о положении шарика, прикреплённого к пружине и колеблющегося вдоль горизонтальной оси Ох, в различные моменты времени.
Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
А) Потенциальная энергия пружины в момент времени 1,0 с максимальна.
Б) Период колебаний шарика равен 4,0 с.
В) Кинетическая энергия шарика в момент времени 2,0 с минимальна.
Г) Амплитуда колебаний шарика равна 30 мм.
Д) Полная механическая энергия маятника, состоящего из шарика и пружины, в момент времени 3,0 с минимальна.
Алгоритм решения
Решение
Согласно утверждению «А», потенциальная энергия пружины в момент времени 1,0 с максимальна. Потенциальная энергия пружины максимальна, когда она отклоняется от положения равновесия на максимальную возможную величину. Из таблицы видно, что в данный момент времени ее отклонение составило 15 мм, что соответствует амплитуде колебаний (наибольшему отклонению от положения равновесия). Следовательно, утверждение «А» — верно.
Согласно утверждению «Б», период колебаний шарика равен 4,0 с. Один период колебаний включает в себя 4 фазы. В течение каждой фазы шарик на пружине проделывает путь, равный амплитуде. Следовательно, мы можем найти период колебаний, умножив время одной фазы на 4. В момент времени t = 0 с, шарик находился в положении равновесия. Первый раз он отклонился на максимальную величину (15 мм) в момент времени t = 1,0 с. Значит, период колебаний равен 1∙4 = 4 с. Следовательно, утверждение «Б» — верно.
Согласно утверждению «В», кинетическая энергия шарика в момент времени 2,0 с минимальна. В этот момент времени, согласно данным таблицы, шарик проходит положение равновесия. В этом положении скорость шарика всегда максимальна. Поэтому кинетическая энергия, которая зависит от квадрата скорости прямо пропорционально, минимальной быть не может. Следовательно, утверждение «В» — неверно.
Согласно утверждению «Г», амплитуда колебаний шарика равна 30 мм. Амплитуда колебаний — есть расстояние от положения равновесия до точки максимального отклонения шарика. В данном случае оно равно 15 мм. Следовательно, утверждение «Г» — неверно.
Согласно утверждению «Д», полная механическая энергия маятника, состоящего из шарика и пружины, в момент времени 3,0 с минимальна. Полная механическая энергия колебательной системы — это совокупность кинетической и потенциальной энергий. И при отсутствии сил трения она остается величиной постоянной. Она лишь превращается из одного вида энергии в другую. Следовательно, утверждение «Д» — неверно.
pазбирался: Алиса Никитина | обсудить разбор | оценить