Что называется испытанием событием приведите примеры испытаний событий
Математика — онлайн помощь
Как любая наука, теория вероятностей имеет свои исходные понятия, через которые определяются другие понятия. К основным понятиям теории вероятностей относятся: испытание, событие, вероятность события.
Изучение явлений происходит путем наблюдений и опытов, проводимых при определенных условиях. Испытанием в теории вероятностей называется осуществление какого-либо комплекса условий, при котором наблюдается данное явление. Предполагается, что данный комплекс условий может быть воспроизведен сколь угодно большое число раз. Итак, в теории вероятностей вместо слов “произведено наблюдение при осуществлении определенного комплекса условий” говорят кратко “произведено испытание”.
Событием называется всякий факт, который может наступить в результате испытания.
События можно классифицировать по степени возможности их появления и по характеру взаимосвязи.
Достоверным называется событие, которое в данном испытании всегда наступает, его обозначают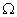 
.
Невозможным называется событие, которое в данном испытании никогда не наступает, его обозначают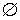 
.
Случайным называется событие, которое в данном испытании может наступить, а может не наступить. Случайные события обозначают заглавными буквами латинского алфавита А, В, С,…
.
События называются несовместными, если появление одного из них исключает появление других событий в данном испытании. В противном случае события называются совместными. Примеры несовместных событий: появление герба и цифры при одном бросании монеты, попадание и промах при одном выстреле. Те же попадание и промах при двух выстрелах являются уже совместными событиями.
Несколько событий образуют полную группу событий, если в результате испытания обязательно наступит хотя бы одно из них. В частности, если события образуют полную группу и несовместны, то в результате испытания появится одно и только одно из этих событий.
Суммой событий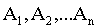 
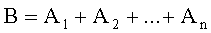
. называется событие, состоящее в наступлении хотя бы одного из этих событий.
.
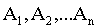
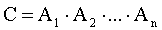
Произведением событий его обозначают . называется событие, состоящее в совместном появлении всех этих событий.
.
Уважаемые студенты
На нашем сайте можно получить помощь по всем разделам математики и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Испытания и события
Основные понятия теории
Вероятностей
Испытания и события
Испытание (опыт, эксперимент) – реализация определенного комплекса условий, который может быть повторен неограниченное число раз. При этом комплекс условий включает в себя случайные факторы, реализация которых в каждом испытании приводит к неоднозначности исхода испытания.
Пример:
1. Подбрасывание монеты.
2. Стрельба по некоторой цели.
Событие – всякий факт, который в результате опыта может произойти или не произойти, или другими словами – это результат опыта независимо от его значения.
Пример:
1. При подбрасывании монеты событием может быть выпадение «герба», выпадение «цифры».
2. При стрельбе по некоторой цели событием может быть поражение цели, промах, поражение определенного сектора цели.
События относительно их появления подразделяется на три группы:
Достоверное событие – событие, которое всегда произойдет в результате испытания.
Пример:
1. При подбрасывании монеты выпадение «герба» или «цифры» есть событие достоверное.
2. При наблюдении за состоянием воды в сосуде при нормальном атмосферном давлении и температуре 20 0 С событие «вода в сосуде находиться в жидком состоянии» есть событие достоверное.
Невозможное событие – событие, которое никогда не произойдет в результате испытания.
Пример:
1. При подбрасывании монеты выпадение «герба» и «цифры» является событиями невозможным.
2. При наблюдении за состоянием воды при нормальном атмосферном давлении и температуре 20 0 С событие «вода в сосуде находится в твердом состоянии» является событием невозможным.
Случайное событие – событие, которое в результате испытания может произойти или не произойти, либо при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по-иному.
Пример:
1. При бросании игральной кости выпадение 6-ти очков есть событие случайное.
2. При стрельбе по цели поражение цели, попадание в определенный сектор цели являются случайными событиями.
События как объекты исследования разделяются на две группы:
Простое событие (элементарный исход) – один из возможных результатов опыта, исключающий появление других результатов. Другими словами простое событие – это результат одного и только одного опыта.
Пример:
2. При одновременном подбрасывании двух монет выпадение двух «гербов», выпадение двух «цифр» являются простыми событиями.
Сложное событие – событие, которое можно разложить на простые события. Другими словами сложное событие – это комбинация простых событий с помощью логических операций.
Пример:
1. При подбрасывании одной монеты выпадение «герба» или «цифры», а также выпадение «герба» и «цифры» есть сложные события.
2. При одновременном подбрасывании двух монет выпадение «герба» на любой из монет – это сложное событие.
События по отношению друг к другу подразделяются на :
7) образующие полную группу;
События называются несовместными,если появление одного из них исключает появление других событий в одном и том же испытании.
Пример:
2. Попадание и промах при одном выстреле – несовместные события.
3. Ни одного попадания, одно попадание, два попадания – несовместные события при двух выстрелах по мишени.
События называются совместными,если появление одного события не исключает появления других событий в данном испытании.
Пример:
2. При одновременном подбрасывании монеты и игральной кости события «выпадения 2-х очков» и «выпадение герба» являются совместными.
События в данном опыте называются равновозможными, если ни одно из них не является более возможным, чем другое.
Пример:
1. Выпадение «герба», выпадение «цифры» при бросании монеты один раз.
2. Появление 1, 2, 3, 4, 5, 6 очков при однократном бросании игральной кости.
3. Появление карты бубновой, червовой, трефовой, пиковой масти при вынимании карты из колоды.
Несколько событий в данном опыте образуют полную группу событий, если в результате опыта непременно должно появиться хотя бы одно из них. Другими словами, появление хотя бы одного из событий полной группы есть достоверное событие. В частности, если события, образующие полную группу попарно несовместны, то в результате испытания появится одно и только одно из этих событий.
Пример:
1. Выпадение «герба», выпадение «цифры» при бросании монеты образуют
полную группу событий.
2. Попадание, промах при выстреле – полная группа событий.
4. Появление не менее 3-х очков, появление не более 4-х очков при бросании игральной кости образуют полную группу событий.
Противоположными называются два несовместных события, образующих полную группу. Иногда говорят, событие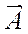 
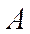
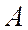
называется противоположным событию 
, если оно состоит в не появлении события 
.
Пример:
1. Безотказная работа всех элементов технической системы, отказ хотя бы одного элемента – противоположные события.
2. Обнаружение не менее двух бракованных изделий в контрольной партии, обнаружение не более одного бракованного изделия – противоположные события.
Вероятность
Определение. Вероятность события – это численная мера степени возможности этого события.
Вероятность события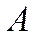 
обозначается 
. Свойства вероятности:
1.Вероятность достоверного события равна 1.
2.Вероятность невозможного события равна 0.
3. Вероятность случайного события есть положительное число между 0 и 1.
,
где 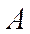— случайное событие.
4. Вероятность любого события удовлетворяет двойному неравенству
,
где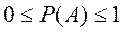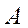 
— любое событие.
Дата добавления: 2015-11-18 ; просмотров: 3832 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Испытания и события. Виды событий. Примеры
К основным понятиям теории вероятности относятся испытания и события.
Под испытанием понимают осуществление некоторого комплекса условий, в результате которого непременно произойдет какое-либо событие. Случайным событием называют такое событие, которое может произойти или не произойти в результате данного испытания.
Случайные события обозначают большими буквами латинского алфавита A, B, C, Dи т.д. Например, событие А – «выпадение герба при подбрасывании монеты», событие В – «выпадение решки при подбрасывании монеты».
Событие называется достоверным, если оно обязательно произойдет в результате данного испытания.
Например, подбрасывание игральной кости – испытание, выпадение целого числа от 1 до 6 – достоверное событие.
Событие называется невозможным, если оно никогда не произойдет в результате данного испытания.
Например, подбрасывание игральной кости – испытание, выпадение 0, выпадение 10 – невозможные события.
События называются несовместными, если никакие два из них не могут появиться одновременно. Если события могут произойти одновременно, то они называютсясовместными.
Например, подбрасывание игральной кости – испытание, событие А – «выпадение 2», событие В – «выпадение 3», событие С – «выпадение четного числа очков». События А и В, В и С– несовместные, т.к. они не могут произойти одновременно, а события А и С – совместны, т.к. могут произойти одновременно при выпадении числа 2.
События называют равновозможными, если ни одно из них не является объективно более возможным, чем другие.
Так в предыдущем примере события А и В равновозможны, а события В и С, А и С неравновозможны в силу условий проведения испытания.
Множество, элементами которого являются все несовместные равновозможные исходы данного испытания, называют пространством элементарных исходов (событий) и обозначают Ω.
Например, при подбрасывании игральной кости пространство W элементарных событий состоит из шести точек: Ω = <1, 2, 3, 4, 5, 6>(выпадение 1, 2, 3, 4, 5 или 6).
Полная группа событий. Примеры.
По́лной гру́ппой собы́тий в теории вероятностей называется система случайных событий такая, что в результате произведенного случайного эксперимента непременно произойдет одно из них.
Определение Править
Пусть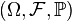 
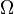
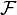
есть вероятностное пространство. Любое разбиение множества 
элементами сигма-алгебры 
называется полной группой событий.
Пример Править
Предположим, проводится подбрасывание монеты. В результате этого эксперимента обязательно произойдет одно из следующих событий:
§ 
: монета упадет орлом;
§ 
: монета упадет решкой;
§ 
: монета упадет на ребро;
§ 
: монета зависнет в воздухе.
§ 
: монету притырит подкидывающий
§ 
: монета превратится в динозавра
§ 
: монета станет летающей тарелкой
§ 
: монета так и не преземлится на землю
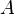
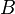
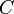
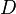
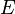
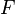
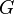
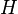
Таким образом, система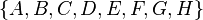 
является полной группой событий.
ИСПЫТАНИЯ И СОБЫТИЯ. ВИДЫ СОБЫТИЙ
К основным понятиям теории вероятности относятся испытания и события.
Под испытанием понимают осуществление некоторого комплекса условий, в результате которого непременно произойдет какое-либо событие. Случайным событием называют такое событие, которое может произойти или не произойти в результате данного испытания.
Случайные события обозначают большими буквами латинского алфавита A, B, C, D и т.д. Например, событие А – «выпадение герба при подбрасывании монеты», событие В – «выпадение решки при подбрасывании монеты».
Событие называется достоверным, если оно обязательно произойдет в результате данного испытания.
Например, подбрасывание игральной кости – испытание, выпадение целого числа от 1 до 6 – достоверное событие.
Событие называется невозможным, если оно никогда не произойдет в результате данного испытания.
Например, подбрасывание игральной кости – испытание, выпадение 0, выпадение 10 – невозможные события.
События называются несовместными, если никакие два из них не могут появиться одновременно. Если события могут произойти одновременно, то они называются совместными.
Например, подбрасывание игральной кости – испытание, событие А – «выпадение 2», событие В – «выпадение 3», событие С – «выпадение четного числа очков». События А и В, В и С– несовместные, т.к. они не могут произойти одновременно, а события А и С – совместны, т.к. могут произойти одновременно при выпадении числа 2.
События называют равновозможными, если ни одно из них не является объективно более возможным, чем другие.
Так в предыдущем примере события А и В равновозможны, а события В и С, А и С неравновозможны в силу условий проведения испытания.
Множество, элементами которого являются все несовместные равновозможные исходы данного испытания, называют пространством элементарных исходов (событий) и обозначают Ω.
Например, при подбрасывании игральной кости пространство W элементарных событий состоит из шести точек: Ω = <1, 2, 3, 4, 5, 6>(выпадение 1, 2, 3, 4, 5 или 6).
Контрольные вопросы:
1. Перечислите основные понятия теории вероятностей.
2. Что в теории вероятностей называют испытанием?
3. Какое событие называют случайным? Приведите примеры случайных событий.
4. Какое событие называют достоверным? Приведите примеры достоверных событий.
5. Какое событие называют невозможным? Приведите примеры невозможных событий.
6. В каком случае два события являются попарно совместными? Приведите примеры двух совместных событий.
7. В каком случае два события являются попарно несовместными? Приведите примеры двух совместных событий.
8. В каком случае два события называются равновозможными? Приведите примеры двух равновозможных событий.
9. В каком случае два события называются неравновозможными? Приведите примеры двух неравновозможных событий.
10. Что называют пространством элементарных исходов?
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
События, виды событий
Опыт, эксперимент, наблюдение явления или некоторого процесса называется испытанием. Примеры испытаний: бросание монеты, выстрел из винтовки, бросание игральной кости (кубика с нанесённой на каждую из шести граней цифры от одного до шести), реализация некоторого физического, механического или технологического процесса и т.д. При бросании монеты исходами (событиями) являются выпадение герба или выпадение цифры, а при бросании игральной кости — выпадение какой либо цифры на верхней грани кости. Испытания сопровождаются их исходами (событиями).
Событие — это качественный и (или) количественный результат испытания (исход), осуществляемого при определённой совокупности условий. Для обозначения событий используются большие буквы латинского алфавита: А, В, С и т.д.
Различают следующие типы событий: случайные события, совместные или несовместные события, достоверные или невозможные события, зависимые или независимые события, равновозможные события, элементарные (простые, неразложимые) события, событие или совокупность событий (исходов), благоприятствующих какому-либо другому событию.
Случайное событие – это результат испытания (или величина), который нельзя заранее спрогнозировать, т.е. нельзя сказать, произойдёт это событие или не произойдёт, или, если событие произойдёт, то неизвестно, какое значение примет результат этого события.
Случайные события – первичные, неопределяемые (в строгом смысле) понятия в теории вероятностей, аналогичные понятиям точки и прямой – в геометрии.
Например, пусть игральная кость с пронумерованными гранями от 1 до 6 подбрасывается два раза. В этом опыте можно рассматривать следующие события: событие А – оба раза выпадет число 1; событие В – хотя бы один раз выпадет число 3; событие С – сумма выпавших чисел равна 8 и т.д.
Событие, которое обязательно наступит (никогда не произойдёт) в данном опыте, называется достоверным (невозможным). Достоверное событие обозначают символом Ω, а невозможное – Æ. Например, в опыте, состоящем в подбрасывании кости один раз – событие А – выпадение одного из чисел 1,2,3,4,5,6 – есть достоверное, а событие В – выпадение числа 7 – невозможное.
Два случайных события называются несовместными, если наступление одного из них исключает наступление другого в одном и том же испытании. (Таким образом, несовместные события не могут наступать одновременно). В противном случае, т.е. если наступление одного события не исключает наступление другого события в одном и том же испытании, то эти события называются совместными. Например, если событие А – появление числа 2 при одном бросании кости, а событие В – появление чётного числа в этом же бросании, то события А и В совместные, а событие С – появление числа 2 при одном бросании кости и событие D – появление числа 3 в этом бросании – события несовместные.
События называются равновозможными, если ни одно из них не является более возможным по сравнению с другими событиями.
События называются независимыми (зависимыми), если числовая характеристика возможности наступления одного события не зависит (зависит) от числовых характеристик наступления других событий (указанные числовые характеристики некоторых событий А, В, С, … называются вероятностями этих событий).
Определение. Совокупность попарно несовместных событий образуют полную группу событий для данного испытания, если в результате каждого испытания происходит одно и только одно из них.
Примеры полных групп событий: а) выпадение герба <Г>и выпадение цифры <Ц>при одном бросании монеты; б) попадание в цель и промах при одном выстреле по мишени; в) выпадение цифр «1», «2», «3», «4», «5», «6» при одном бросании кости.
Множество всех элементарных событий называется пространством элементарных событий и обозначается Ω. Например, в результате бросания кости выпадение цифры i = 1, 2, 3, 4, 5, 6 образует пространство Ω = <1, 2, 3, 4, 5, 6>.
Элементарные события, составляющие пространство Ω, обозначаются ω1, ω2, …, ω6.
Замечание. Кроме случайных событий в теории вероятностей вводятся в рассмотрение случайные величины. Случайная величина – это переменная, которая в результате испытания в зависимости от случая принимает одно из возможных значений. Случайные величины в данном пособии рассматриваются более подробно в главе 3.