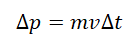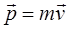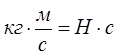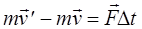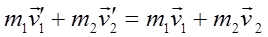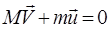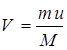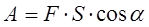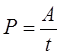Что называется импульсом это скалярная или векторная величина
Импульс тела. Закон сохранения импульса
1. Опыты и наблюдения свидетельствуют о том, что результат действия силы (взаимодействия) зависит от времени её действия. Так, если к штативу на нити подвесить
тяжёлую гирю, к которой привязана ещё одна нить снизу, и резко дернуть нижнюю нить, то она оборвётся, а верхняя нить останется целой. Если же теперь медленно потянуть
нижнюю нить, то оборвётся верхняя нить. Поэтому для характеристики действия силы вводят величину, называемую импульсом силы.
Импульсом силы называют векторную величину, равную произведению силы и времени её действия \( (\vec
Единица импульса силы \( [\,F\cdot t\,] \) = 1 Н · с.
2. С другой стороны, результат действия силы зависит и от характеристик тела, на которое эта сила действует.
Зависимость результата действия силы от массы тела можно проиллюстрировать с помощью следующего простого примера. Летящий с некоторой скоростью футбольный мяч, ударяясь о пустую картонную коробку, сдвинет её с места, а, ударяясь о такую же коробку, заполненную металлическими предметами, скорее всего, отскочит от неё, а коробка при этом останется неподвижной.
Пуля, летящая со скоростью 2 м/с, при попадании в деревянную стенку в лучшем случае оставит на ней вмятину, а пуля, летящая со скоростью 200 м/с, стенку пробьёт. Таким образом, результат действия силы зависит от массы и скорости взаимодействующих тел.
Импульс — величина векторная, поскольку масса — величина скалярная, а скорость — векторная.
Импульс — величина относительная, его значение зависит от выбора системы отсчёта, поскольку относительной величиной является скорость.
4. Импульс силы и изменение импульса тела связаны между собой.
Запишем второй закон Ньютона: \( \vec
В левой части равенства стоит импульс силы; в правой части — разность конечного и начального импульсов тела, т.е. изменение импульса тела. \( \vec
Таким образом, импульс силы равен изменению импульса тела.
Это иная формулировка второго закона Ньютона. Именно в таком виде сформулировал свой закон Ньютон.
Силы, с которыми тела системы взаимодействуют между собой, называют внутренними силами.
Помимо внутренних сил, на тела системы действуют внешние силы. Так взаимодействующие тела притягиваются к Земле. Сила тяготения является в данном случае внешней силой. Если тела движутся, то на них действует сила сопротивления воздуха, сила трения. Они тоже являются внешними силами по отношению к системе, которая в данном случае состоит из двух тел. Ни Земля, ни воздух в эту систему тел не входят.
Внешними силами называются силы, которые действуют на тела системы со стороны других тел.
Будем рассматривать такую систему тел, на которую не действуют внешние силы.
Замкнутой системой тел называют систему тел, взаимодействующих между собой и не взаимодействующих с другими телами. В замкнутой системе действуют только внутренние силы, внешние силы на неё не действуют.
В левой части равенства стоит сумма импульсов тел до взаимодействия, в правой части — сумма импульсов тел после взаимодействия. Как видно, импульс каждого тела при взаимодействии изменился, а сумма импульсов осталась неизменной.
Геометрическая сумма импульсов тел, входящих в замкнутую систему, остаётся постоянной при любых взаимодействиях тел этой системы между собой.
В этом состоит закон сохранения импульса.
7. Замкнутая система — это идеализация. В реальном мире нет таких систем, на которые не действовали бы внешние силы. Однако в ряде случаев реальные системы взаимодействующих тел можно рассматривать как замкнутые. Это возможно, когда внутренние силы много больше внешних сил, или когда время взаимодействия мало, или когда внешние силы уравновешивают друг друга. Кроме того, в ряде случаев равна нулю проекция внешних сил на какое-либо направление. В этом случае закон сохранения импульса выполняется для проекций импульсов взаимодействующих тел на это направление.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Тело двигалось под действием силы 10 Н в течение 5 с. Чему равно изменение импульса тела?
1) 2 Н/с
2) 5 Н·с
3) 50 Н·с
4) нельзя дать ответ, т.к. неизвестны масса и скорость тела
2. Чему равен импульс автомобиля массой 1,5 т, движущегося со скоростью 20 м/с в системе отсчёта, связанной с автомобилем, движущимся в ту же сторону с той же скоростью?
1) 0
2) 15 000 кг·м/с
3) 30 000 кг·м/с
4) 60 000 кг·м/с
3. Чему равен импульс автомобиля массой 1,5 т, движущегося со скоростью 20 м/с в системе отсчёта, связанной с автомобилем, движущимся с той же скоростью, но в противоположную сторону?
1) 0
2) 15 000 кг·м/с
3) 30 000 кг·м/с
4) 60 000 кг·м/с
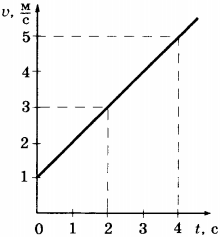
4. На графике показаны изменения скорости велосипедиста с течением времени. Чему равно изменение импульса велосипедиста через 4 с после начала движения, если его масса 50 кг?
1) 200 кг·м/с
2) 2500 кг·м/с
3) 2000 кг·м/с
4) 2500 кг·м/с
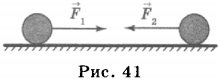
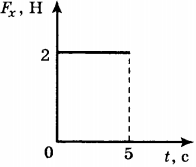
5. Тело движется в положительном направлении оси \( Ox \) . На рисунке представлен график зависимости от времени \( t \) проекции силы \( F_x \) , действующей на тело. В интервале времени от 0 до 5 с проекция импульса тела на ось \( Ox \)
1) уменьшается на 5 кг·м/с
2) не изменяется
3) увеличивается на 10 кг·м/с
4) увеличивается на 5 кг·м/с
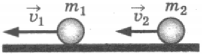
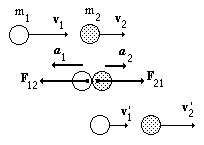
6. Два шара массой \( m_1 \) и \( m_2 \) движутся в одном направлении со скоростями соответственно \( x_1 \) и \( x_2 \) по гладкому горизонтальному столу (см. рисунок). Полный импульс \( p \) системы шаров равен по модулю
1) \( p=m_2x_2-m_1x_1 \) и направлен налево ←
2) \( p=m_1x_1-m_2x_2 \) и направлен вправо →
3) \( p=m_1x_1+m_2x_2 \) и направлен налево ←
4) \( p=m_1x_1-m_2x_2 \) и направлен вправо →
7. Два шарика массой 50 г и 100 г движутся со скоростью 0,6 м/с и 0,4 м/с соответственно. Направления движения шариков составляют угол 90°. Модуль суммарного импульса шариков равен
1) 0,15 кг·м/с
2) 0,07 кг·м/с
3) 0,05 кг·м/с
4) 0,01 кг·м/с
9. Масса мальчика в 3 раза меньше массы лодки. В момент прыжка с неподвижной лодки скорость мальчика равна 1,5 м/с. При этом лодка приобретает скорость, равную
1) 4,5 м/с
2) 2 м/с
3) 0,5 м/с
4) 0 м/с
10. Закон сохранения импульса справедлив:
А. Для замкнутой системы тел
Б. Для любой системы тел.
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
11. Установите соответствие между физическими величинами (в левом столбце таблицы) и их единицами (в правом столбце таблицы). В ответе запишите выбранные цифры под соответствующими буквами
ВЕЛИЧИНА
A. Импульс
Б. Скорость
B. Ускорение
ЕДИНИЦА
1) метр/секунда (1 м/с)
2) ньютон (1 Н)
3) метр/секунда 2 (1 м/с 2 )
4) джоуль (1 Дж)
5) ньютон·секунда (1 Н·с)
12. Из приведённого перечня выберите 2 правильных утверждения и запишите их номера в таблицу.
1) Закон сохранения импульса справедлив для любой системы тел.
2) Импульс тела — величина скалярная.
3) Закон сохранения импульса справедлив для замкнутой системы тел.
4) Изменение импульса тела равно импульсу силы.
5) Закон сохранения импульса не применим к незамкнутой системе тел ни при каких условиях.
Часть 2
Импульс тела, закон сохранения импульса
теория по физике 🧲 законы сохранения
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости ( p ↑↓ v ), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p 1отн2— импульс первого тела относительно второго, m1 — масса первого тела, v 1отн2 — скорость первого тела относительно второго, v 1и v 2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
Изменение импульса тела
∆ p — изменение импульса тела, p — конечный импульс тела, p 0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар
Конечный импульс тела:
Модуль изменения импульса тела равен модулю его начального импульса:
Абсолютно упругий удар
Модули конечной и начальной скоростей равны:
Модули конечного и начального импульсов равны:
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:
Пуля пробила стенку
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов:
Радиус-вектор тела повернул на 180 градусов
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса:
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали
Модули конечной и начальной скоростей равны:
Модули конечного и начального импульсов равны:
Угол падения равен углу отражения:
Модуль изменения импульса в этом случае определяется формулой:
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
F ∆t — импульс силы, ∆ p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Реактивное движение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
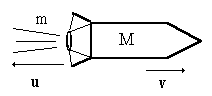
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Суммарный импульс системы тел
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
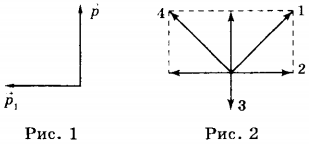
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Закон сохранения импульса
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
Отсюда скорость равна:
Импульс частицы до столкновения равен − p 1, а после столкновения равен − p 2, причём p1 = p, p2 = 2p, − p 1⊥ − p 2. Изменение импульса частицы при столкновении Δ − p равняется по модулю:
Алгоритм решения
Решение
Запишем исходные данные:
Δ p = √ p 2 1 + p 2 2
Подставим известные данные:
Δ p = √ p 2 + ( 2 p ) 2 = √ 5 p 2 = p √ 5
pазбирался: Алиса Никитина | обсудить разбор | оценить

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
ИМПУЛЬС ТЕЛА. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА



ИМПУЛЬС ТЕЛА. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
Импульс тела (р)- это векторная величина, которая равна произведению массы тела на его скорость:
Вектор импульса тела сонаправлен с направлением скорости тела. Единица измерения импульса в СИ:
Изменение импульса тела равно импульсу действующей на него внешней силы:
где 
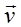
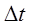
Система тел, на которую не действуют внешние силы, является замкнутой (изолированной).
Закон сохранения импульса: в замкнутой системе векторная сумма импульсов всех тел есть величина постоянная:
Реактивное движение- это движение, которое возникает при выбросе телом вещества.
Пример реактивного движения ракеты массой М, из сопла которой при сгорании топлива выбрасываются газы массой m со скоростью 
Модуль скорости V ракеты:
ЭНЕРГИЯ. РАБОТА. МОЩНОСТЬ. ЗАКОН СОХРАНЕНИЯ ПОЛНОЙ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
Механической энергией называется способность тела совершать работу.
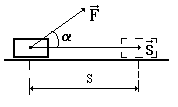
Работа является мерой передачи энергии от одного тела к другому или превращения энергии из одного вида в другой.
Единица измерения работы в СИ: Джоуль (Дж); Дж = Н м
Формула кинетической энергии тела массой m, движущегося со скоростью v:
Сумма потенциальной и кинетической энергии тела называется полной механической энергией тела (системы тел).
Закон сохранения полной механической энергии:
в замкнутой системе, между телами которой действуют только консервативные силы (силы тяжести и/или силы упругости) полная механическая энергия есть величина постоянная:
Импульс
И́мпульс (Количество движения) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:

В более общем виде, справедливом также и в релятивистской механике, определение имеет вид:
Содержание
История появления термина
Ещё в первой половине XVII века понятие импульса введено Рене Декартом. Так как физическое понятие массы в то время отсутствовало, он определил импульс как произведение «величины тела на скорость его движения». Позже такое определение было уточнено Исааком Ньютоном. Согласно Ньютону, «количество движения есть мера такового, устанавливаемая пропорционально скорости и массе».
«Школьное» определение импульса
В классической механике полным импульсом системы материальных точек называется векторная величина, равная сумме произведений масс материальных точек на их скорости:
соответственно величина 
Если мы имеем дело с телом конечного размера, не состоящим из дискретных материальных точек, для определения его импульса необходимо разбить тело на малые части, которые можно считать материальными точками и просуммировать по ним, в результате получим:
Импульс системы, на которую не действуют никакие внешние силы (или они скомпенсированы), сохраняется во времени:

Сохранение импульса в этом случае следует из второго и третьего закона Ньютона: написав второй закон Ньютона для каждой из составляющих систему материальных точек и просуммировав по всем материальным точкам, составляющим систему, в силу третьего закона Ньютона получим равенство (*).
В релятивистской механике трёхмерным импульсом системы невзаимодействующих материальных точек называется величина

Для замкнутой системы не взаимодействующих материальных точек эта величина сохраняется. Однако трёхмерный импульс не есть релятивистски инвариантная величина, так как он зависит от системы отсчёта. Более осмысленной величиной будет четырёхмерный импульс, который для одной материальной точки определяется как
На практике часто применяются следующие соотношения между массой, импульсом и энергией частицы:
В принципе, для системы невзаимодействующих материальных точек их 4-импульсы суммируются. Однако для взаимодействующих частиц в релятивистской механике следует учитывать импульсы не только составляющих систему частиц, но и импульс поля взаимодействия между ними. Поэтому гораздо более осмысленной величиной в релятивистской механике является тензор энергии-импульса, который в полной мере удовлетворяет законам сохранения.
Обобщённый импульс в теоретической механике
В теоретической механике обобщённым импульсом называется частная производная лагранжиана системы по обобщённой скорости
В случае, если лагранжиан системы не зависит от некоторой обобщённой координаты, то в силу уравнений Лагранжа 
Для свободной частицы функция Лагранжа имеет вид: 
Независимость лагранжиана замкнутой системы от её положения в пространстве следует из свойства однородности пространства: для хорошо изолированной системы её поведение не зависит от того, в какое место пространства мы её поместим. По теореме Нётер из этой однородности следует сохранение некоторой физической величины. Эту величину и называют импульсом (обычным, не обобщённым).
Обобщённый импульс в электромагнитном поле
В электромагнитном поле полный импульс частицы равен:
где 
Формальное определение импульса
Импульсом называется сохраняющаяся физическая величина, связанная с однородностью пространства (инвариант относительно трансляций).
Импульс электромагнитного поля
Электромагнитное поле, как и любой другой материальный объект, обладает импульсом, который легко можно найти, проинтегрировав вектор Пойнтинга по объёму:

Существованием импульса у электромагнитного поля объясняется, например, такое явление, как давление электромагнитного излучения.
Импульс в квантовой механике
Формальное определение
В квантовой механике оператором импульса частицы называют оператор — генератор группы трансляций. Это эрмитов оператор, собственные значения которого отождествляются с импульсом системы частиц. В координатном представлении для системы нерелятивистских частиц он имеет вид
где 

Для замкнутой системы (
Определение через волны де Бройля
Формула де Бройля связывает импульс и длину волны де Бройля.
Модуль импульса обратно пропорционален длине волны 
В векторном виде это записывается как 


См. также
Литература
Полезное
Смотреть что такое «Импульс» в других словарях:
импульс — импульс, а … Русский орфографический словарь
ИМПУЛЬС — (лат., от impellere толкать). Внушение, побуждение, понуждение, толчок к чему либо. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ИМПУЛЬС 1) толчок, побуждающий к движению; 2) сильное нравственное побуждение.… … Словарь иностранных слов русского языка
ИМПУЛЬС — в физике, 1) мера механического движения (то же, что количество движения). Импульсом обладают все формы материи, в том числе электромагнитные, гравитационные и другие поля (смотри Поля физические). В простейшем случае механического движения… … Современная энциклопедия
ИМПУЛЬС — в физике: 1) мера механического движения (то же что количество движения). Импульсом обладают все формы материи, в т. ч. электромагнитные и гравитационные поля;..2) импульс силы мера действия силы за некоторый промежуток времени; равен… … Большой Энциклопедический словарь
ИМПУЛЬС — внезапное и быстроисчезающее повышение какого либо параметра в системе (давления, температуры, освещённости и др.), а также единичный сигнал конечной энергии, существенно отличный от нуля в течение ограниченного времени; характеризуется фазой и… … Большая политехническая энциклопедия
импульс — а, м. mpulsion f., нем. Impulsion, Impuls. Побудительная причина к какому л. действию; толчок. побуждение. БАС 1. Граф < Салтыков> нечто временное и частное, усилен мною и моею честью, меняет ту импульзию на глупые одни pets interêts. 15 17 … Исторический словарь галлицизмов русского языка
ИМПУЛЬС — (лат.) побуждение, толчок; импульсивный – побудительный, определенный импульсом, совершаемый без (долгого) размышления; см. также Спонтанный. В физике импульс (произведение силы на время, в течение которого действует сила [k t]) есть увеличение… … Философская энциклопедия
ИМПУЛЬС — (от лат. impulsus толчок, побуждение), процесс в нервной системе, приводящий иннервируемые органы в состояние деятельности или состояние торможения. Ко всем эффекторным органам И. приходят по эфферентному нерву. В нормальных условиях И.в… … Большая медицинская энциклопедия
импульс — 1. Толчок к чему либо, побуждение к совершению чего либо; причина, вызывающая некое действие. 2. Импульс электрический быстрый кратковременный скачок электрического тока или напряжения. Словарь практического психолога. М.: АСТ, Харвест. С. Ю.… … Большая психологическая энциклопедия