Что называется гранями многогранника
Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Урок № 13. Многогранники
Перечень вопросов, рассматриваемых в теме:
Многогранник – геометрическое тело, ограниченное конечным числом плоских многоугольников.
Грани многогранника – многоугольники, ограничивающие многогранники.
Ребра многогранника – стороны граней многогранника.
Вершины многогранника – концы ребер многогранника (вершины граней многогранника).
Диагональ многогранника – отрезок, соединяющий две вершины, не принадлежащие одной грани.
Выпуклый многогранник – многогранник, расположенный по одну сторону от плоскости его любой грани.
Невыпуклый многогранник – многогранник, у которого найдется по крайней мере одна грань такая, что плоскость, проведенная через эту грань, делит данный многогранник на две или более частей.
Атанасян Л. С., В. Ф. Бутузов, С. Б. Кадомцев и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы: учеб. Для общеобразоват. организаций: базовый и углубл. уровния. – М.: Просвещение, 2014. – 255 с. (стр. 58, стр. 60 – 61)
Долбилин Н. П. Жемчужины теории многогранников М. : – МЦНМО, 2000. – 40 с.: ил. (стр. 27 – 31)
Открытые электронные ресурсы:
Долбилин Н. П. Три теоремы о выпуклых многогранниках. Журнал Квант.
Теоретический материал для самостоятельного изучения
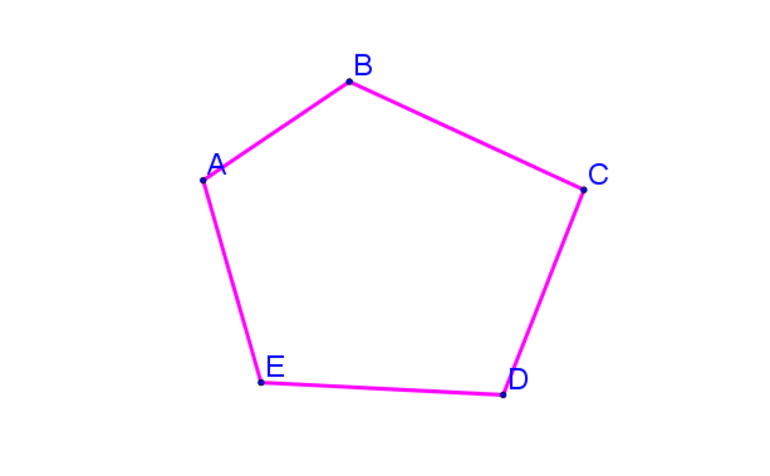
К определению понятия многогранника существует два подхода. Проведем аналогию с понятием многоугольника. Напомним, что в планиметрии под многоугольником мы понимали замкнутую линию без самопересечений, составленную из отрезков (рис. 1а). Также многоугольник можно рассматривать как часть плоскости, ограниченную этой линией, включая ее саму (рис. 1б). При изучении тел в пространстве мы будем пользоваться вторым толкованием понятия многоугольник. Так, любой многоугольник в пространстве есть плоская поверхность.
Б)
Рисунок 1 – разные подходы к определению многоугольника
Вторая трактовка понятия определяет многогранник как геометрическое тело, ограниченное конечным числом плоских многоугольников.
В дальнейшем, мы будем использовать вторую трактовку понятия многогранника.
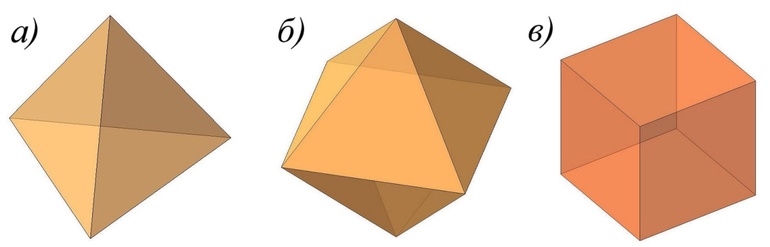
Уже известные вам тетраэдр и параллелепипед являются многогранниками. Потому что они являются геометрическими телами, ограниченные конечным числом плоских многоугольников. Еще один пример многогранника — октаэдр (рис. 2)
Рисунок 2 – изображение октаэдра
Многоугольники, ограничивающие многогранник, называются его гранями. Так, у тетраэдра и октаэдра гранями являются треугольники. У тетраэдра 4 грани, отсюда и его название от греч. τετρά-εδρον — четырёхгранник. У октаэдра 8 граней, а от греческого οκτάεδρον от οκτώ «восемь» + έδρα «основание».
Стороны граней называются ребрами, а концы ребер — вершинами многогранника. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.
Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани. В остальных случаях многогранник называется невыпуклым (рис.3).
Рисунок 3 – Виды многогранников
Сумма плоских углов при вершине выпуклого многогранника
Рисунок 4 – сумма плоских углов пи вершине многогранника
Теорема Эйлера. Пусть В — число вершин выпуклого многогранника, Р — число его ребер, а Г — число его граней. Тогда верно равенство В – Р+Г= 2.
Теорема Эйлера играет огромную роль в математике. С ее помощью было доказано огромное количество теорем. Находясь в центре постоянного внимания со стороны математиков, теорема Эйлера получила далеко идущие обобщения. Более того, эта теорема открыла новую главу в математике, которая называется топологией.
Примеры и разбор решения заданий тренировочного модуля
Задание 1. Какие из перечисленных объектов НЕ могут быть элементами многогранника? Укажите номера в порядке возрастания.
Элементы многогранника, которые мы выделили: ребра, грани, вершины и диагонали. Ребро и диагональ многогранника – это отрезок. Грань многогранника – многоугольник, или иначе ограниченная часть плоскости. Вершины представляют собой точки. Таким образом, элементами многогранника не могут быть плоскость, луч, многогранник, прямая.
Задание 2. Сопоставьте геометрическим фигурам их вид
Б) пространственная фигура
Вспомним, что изобразить пространственную фигуру можно разными способами. Например, с помощью теней или изображением невидимых линий пунктиром. Так, среди всех изображений плоской фигурой является фигура под номером 1.
Многогранник – геометрическое тело, ограниченное конечным числом плоских многоугольников. Только на изображении 2 фигура ограничена многоугольниками. Таким образом, получаем следующий ответ: 1-А, 2-В, 3-Б
Что такое многогранник? Примеры
Примеры многогранников:
1) каждая сторона одного является одновременно стороной другого (но только одного), называемого смежным с первым (по этой стороне);
Многогранник называется выпуклым, если он лежит по одну сторону от плоскости любой его грани.
Из этого определения следует, что все грани выпуклого многогранника являются плоскими многоугольниками. Поверхность выпуклого многогранника состоит из граней, которые лежат в разных плоскостях. При этом ребрами многогранника являются стороны многоугольников, вершинами многогранника – вершины граней, плоскими углами многогранника – углы многоугольников – граней.
Выпуклый многогранник, все вершины которого лежат в двух параллельных плоскостях, называется призматоидом. Призма, пирамида и усеченная пирамида – частные случаи призматоида. Все боковые грани призматоида являются треугольниками или четырехугольниками, причем четырехугольные грани – это трапеции или параллелограммы.
Популярное
Изобретение календаря замечательное событие для человечества. То, что год состоит из 12ти месяцев ни для кого не секрет. С тех пор люди самыми различными способами группируют.
Когда мы готовили 36-ой выпуск «Волшебные грани», у наших коллег возник вопрос: «Почему мы опять собираемся говорить о правильных многогранниках.
Звезда — это образ божественной идеи, божественной воли, согласно которой возник и начал вращаться в Пространстве и жить наш Свет, Мир.
Для Вашего удобства мы снизили стоимость доставки наборов «Волшебные грани» в разы!
Нам нужны еще фонарики Джека в форме тыквы. Кто же нам поможет? Может быть Архимед?
Почему бумага? Иногда приходится слышать вопрос: «Почему вы выбрали для сборки многогранников такой материал как бумага (или точнее дизайнерский картон)? Это же.
Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Урок № 13. Многогранники
Перечень вопросов, рассматриваемых в теме:
Многогранник – геометрическое тело, ограниченное конечным числом плоских многоугольников.
Грани многогранника – многоугольники, ограничивающие многогранники.
Ребра многогранника – стороны граней многогранника.
Вершины многогранника – концы ребер многогранника (вершины граней многогранника).
Диагональ многогранника – отрезок, соединяющий две вершины, не принадлежащие одной грани.
Выпуклый многогранник – многогранник, расположенный по одну сторону от плоскости его любой грани.
Невыпуклый многогранник – многогранник, у которого найдется по крайней мере одна грань такая, что плоскость, проведенная через эту грань, делит данный многогранник на две или более частей.
Атанасян Л. С., В. Ф. Бутузов, С. Б. Кадомцев и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы: учеб. Для общеобразоват. организаций: базовый и углубл. уровния. – М.: Просвещение, 2014. – 255 с. (стр. 58, стр. 60 – 61)
Долбилин Н. П. Жемчужины теории многогранников М. : – МЦНМО, 2000. – 40 с.: ил. (стр. 27 – 31)
Открытые электронные ресурсы:
Долбилин Н. П. Три теоремы о выпуклых многогранниках. Журнал Квант.
Теоретический материал для самостоятельного изучения
К определению понятия многогранника существует два подхода. Проведем аналогию с понятием многоугольника. Напомним, что в планиметрии под многоугольником мы понимали замкнутую линию без самопересечений, составленную из отрезков (рис. 1а). Также многоугольник можно рассматривать как часть плоскости, ограниченную этой линией, включая ее саму (рис. 1б). При изучении тел в пространстве мы будем пользоваться вторым толкованием понятия многоугольник. Так, любой многоугольник в пространстве есть плоская поверхность.
Б)
Рисунок 1 – разные подходы к определению многоугольника
Вторая трактовка понятия определяет многогранник как геометрическое тело, ограниченное конечным числом плоских многоугольников.
В дальнейшем, мы будем использовать вторую трактовку понятия многогранника.
Уже известные вам тетраэдр и параллелепипед являются многогранниками. Потому что они являются геометрическими телами, ограниченные конечным числом плоских многоугольников. Еще один пример многогранника — октаэдр (рис. 2)
Рисунок 2 – изображение октаэдра
Многоугольники, ограничивающие многогранник, называются его гранями. Так, у тетраэдра и октаэдра гранями являются треугольники. У тетраэдра 4 грани, отсюда и его название от греч. τετρά-εδρον — четырёхгранник. У октаэдра 8 граней, а от греческого οκτάεδρον от οκτώ «восемь» + έδρα «основание».
Стороны граней называются ребрами, а концы ребер — вершинами многогранника. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.
Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани. В остальных случаях многогранник называется невыпуклым (рис.3).
Рисунок 3 – Виды многогранников
Сумма плоских углов при вершине выпуклого многогранника
Рисунок 4 – сумма плоских углов пи вершине многогранника
Теорема Эйлера. Пусть В — число вершин выпуклого многогранника, Р — число его ребер, а Г — число его граней. Тогда верно равенство В – Р+Г= 2.
Теорема Эйлера играет огромную роль в математике. С ее помощью было доказано огромное количество теорем. Находясь в центре постоянного внимания со стороны математиков, теорема Эйлера получила далеко идущие обобщения. Более того, эта теорема открыла новую главу в математике, которая называется топологией.
Примеры и разбор решения заданий тренировочного модуля
Задание 1. Какие из перечисленных объектов НЕ могут быть элементами многогранника? Укажите номера в порядке возрастания.
Элементы многогранника, которые мы выделили: ребра, грани, вершины и диагонали. Ребро и диагональ многогранника – это отрезок. Грань многогранника – многоугольник, или иначе ограниченная часть плоскости. Вершины представляют собой точки. Таким образом, элементами многогранника не могут быть плоскость, луч, многогранник, прямая.
Задание 2. Сопоставьте геометрическим фигурам их вид
Б) пространственная фигура
Вспомним, что изобразить пространственную фигуру можно разными способами. Например, с помощью теней или изображением невидимых линий пунктиром. Так, среди всех изображений плоской фигурой является фигура под номером 1.
Многогранник – геометрическое тело, ограниченное конечным числом плоских многоугольников. Только на изображении 2 фигура ограничена многоугольниками. Таким образом, получаем следующий ответ: 1-А, 2-В, 3-Б
Многогранники
Большинство заданий 8 по стереометрии решаются достаточно просто. Нужно лишь научиться применять простейшие формулы и немного потренировать пространственную интуицию. Для того чтобы успешно решать такие задачи, нужно знать:
В этой и последующих статьях речь пойдет о задачах с многогранниками. Начнем с определения многогранника:
В школьном курсе рассматриваются выпуклые многогранники. Это многогранники, для которых верно следующее утверждение: для любой плоскости, проходящей через одну из граней многогранника, многогранник находится целиком по одну сторону от этой плоскости. Многогранник является выпуклым тогда и только тогда, когда отрезок, соединяющий любые две точки многогранника, полностью принадлежит многограннику.
Каждая грань такого многогранника будет выпуклым многоугольником. При этом обратное утверждение не верно: если каждая грань многогранника — выпуклый многоугольником, то он необязательно выпуклый!
Разновидностей многогранников существует множество. Например, любая 3D-модель из компьютерной игры представляет собой некоторый (возможно, очень сложный) многогранник. Чем он сложнее, тем точнее описывает реальный объект. Однако изучать свойства многогранников легче на простых моделях. Устройство многогранников важно знать и понимать инженерам, дизайнерам и художникам, а также всем, кто хочет лучше понимать взаимосвязи объектов в пространстве.
Мы же рассмотрим наиболее важные и часто встречающиеся в приложениях классы многогранников:
На самом деле параллелепипед — это частный случай призмы, но мы его рассмотрим отдельно, поскольку он очень важный.
Из статей об этих многогранниках вы узнаете:
Основные понятия
Определение многогранника включает в себя такое понятие, как геометрическое тело, созданное из плоских многоугольников. Их число конечное. От формы каждого из них напрямую зависят свойства итоговой фигуры. Их делят на 2 типа:
Поскольку многогранники рассматриваются в трехмерном евклидовом пространстве, они относятся к стереометрии. А их многоугольники лежат в двумерной плоскости, что относится к планиметрии. Поэтому основные свойства и понятия формируются, включая в себя обе эти науки.
Параметры фигуры
Правильные многогранники
Правильные многогранники — фигуры, грани которых представляют собой многоугольники с равными углами и сторонами. Также они называются Платоновыми телами. Всего существует 5 соответствующих тел, подробные характеристики которых представлены в таблице.
Правильные многогранники изучались древними греками. Однако первые модели в орнаменте и по отдельности появились намного раньше. Например, археологами были найдены вырезанные каменные шары в Шотландии, которые датируются поздним неолитом (соответственно, за 1000 лет до жизни и деятельности Платона).
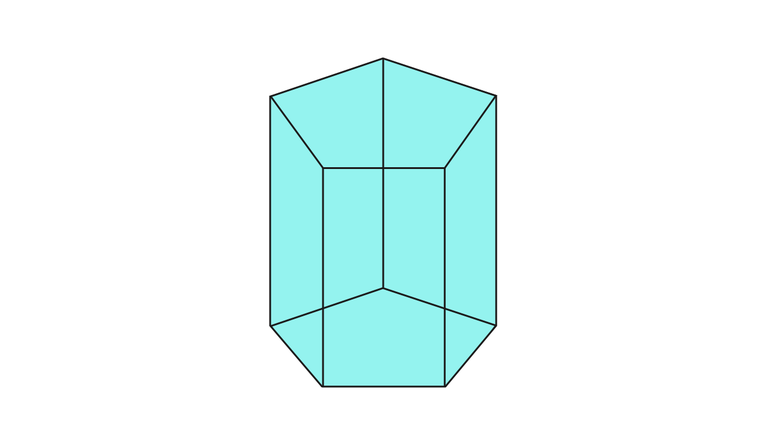
Призма и ее особенности
Геометрическое тело называют прямым, если каждое ребро лежит перпендикулярно основанию. Также они становятся высотами. Когда грани идентичны, многоугольник считается правильным, и его диагональное сечение образует параллелограмм.
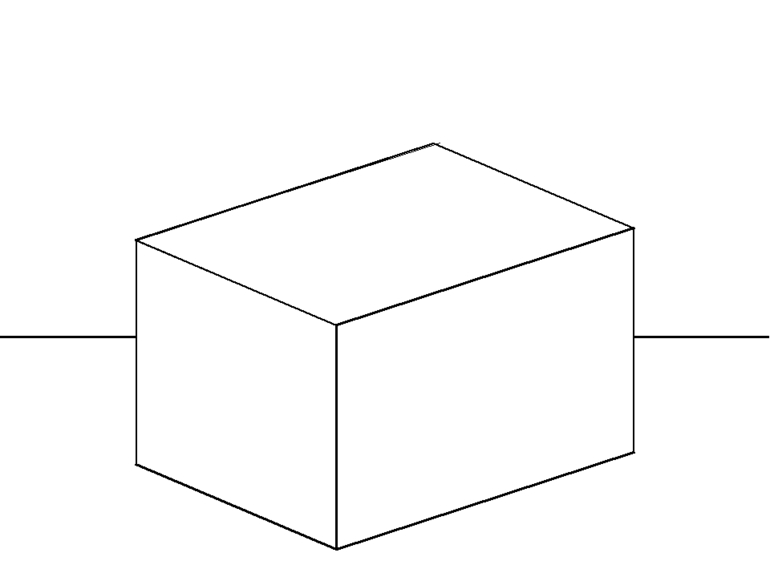
Характеристики параллелепипеда
Параллелепипед — многогранник, основанием и гранями которого является параллелограмм. Фигура характеризуется как неправильная. Основные характеристики:
Когда все грани параллелограмма являются прямоугольными, фигура характеризуется, как прямоугольная. Длина каждого ребра считается линейным размером. У такой фигуры есть три измерения. При этом справедлива формула d² = a² + b² + c². При расчетах руководствуются и другими. Для объема : V = abc, для площади многогранника: S=2·(ab+ bc +ac).
Пирамида и ее величины
Пирамида представляет собой многогранник и многоугольник. Особенности фигуры:
Если пирамиду разделяет плоскость, параллельная нижней, она делит ее на две части. Причем верхняя пропорционально равна главной фигуре. Когда основанием является квадрат, геометрическое тело называется правильным. Гранями ее считаются равнобедренные треугольники.