Что называется графической точностью поперечного масштаба
Предельная и графическая точность масштаба
Горизонтальное расстояние на местности, соответствующее в данном масштабе 0,1 мм, на плане называется предельной точностью масштаба.
Горизонтальное расстояние на местности, соответствующее в данном масштабе 0,2 мм, на
плане называется графической точностью масштаба.
Такие точности измерений по каре могут быть достигнуты применением поперечного масштаба
| Числ. масштаб | 1:1000 | 1:2000 | 1:10000 |
| Точность масштаба, м. | |||
| -предельная | 0,1 | 0,2 | 1,0 |
| — графическая | 0,2 | 0,4 | 2,0 |
Вопрос. Системы координат, применяемые в геодезии
Положение точек поверхности земли определяется координатами.
Координаты —величины, определяющие положение точки на поверхности, в пространстве, на плоскости.
Системы координат —составляют исходные плоскости, линии, точки.
Все системы координат, применяемые в геодезии, можно разделить на две группы:
Пространственные системы координат:
1. Географическая система координат (обще название), которая объединяет астрономическую и геодезическую системы координат. Будем рассматривать геодезическую систему координат.
2.Пространственная полярная система координат.
Плоские системы координат:
1. Зональная система плоских прямоугольных координат.
2. Плоская условная система прямоугольных координат.
3. Система плоских полярных координат.
Плоская прямоугольная система координат.
А) зональная система плоских прямоугольных координат
В соответствии с принятой равноугольной поперечно-цилиндрической проекцией Гаусса, в геодезии принята зональная система плоских прямоугольных координат.
Положение точек земной поверхности определяется прямоугольными координатами Х и У. Оси координат в геодезии развернуты на 90 градусов по сравнению с декартовой системой координат.
Счет абсциссведется от экватора к северу со знаком плюс. К югу — со знаком минус. Для территории нашей страны абсциссы положительны, поэтому знак перед значением абсциссы не ставится (опускается).
Ординатык востоку от осевого меридиана положительны, а к западу отрицательны.
Для того, чтобы все значения ординат были со знаком плюс, счет их ведется от условного меридиана, вынесенного на запад на 500 км, т.е. осевому меридиану придается значение 500 000 м. при этом впереди значения ординаты пишут номер зоны.
Исправленную таким образом ординату называют приведеннойили условной,а координаты называют условнымиили действительными.
Связь между условными координатами и их
Х’, У’ — действительные значения координат
Х, У — условные значения координат.
Хм = 5 650 450, где 5 650 км, 450 м
Ум = 3 250 550, где 3 — номер зоны, 250 км, 550 м.
Это полные условные прямоугольные координаты точки.
Полные действительные координаты:
Х’ =5 650450
Точка М расположена в третьей зоне в 249 км 550 м к западу от осевого меридиана (250 550 — 500 000) и к северу от экватора на удалении 5 650 км 450 м.
Для измерения прямых координат на карты наносится координатная сетка.Координаты, в которых указываются только десятки и единицы километров и метров, называются сокращенными.
Они применяются при работе в пределах границ карты, плана. Система применяется при составлении планов, карт.
Б) Система плоских полярных координат.
Элемент системы:
— начало координатной системы (полюс)
Возможные варианты элементов системы координат: Полярная ось — любое ориентирное направление (А, Ам, а, сторона теодолитного хода и т.д.)
Начало координат: — точка стояния
— точка теодолитного хода
Координаты, определяющие положение точки:
— горизонтальный угол между полярной осью и направлением на определяемую точку 
— горизонтальное расстояние от полюса до определяемой точки (d).
Применение системы:
— при теодолитной съемке
— при выполнении разбивочных работ (вынос точки в натуру).
В) Плоская условная система прямоугольных координат
Элементы системы:
-начало — произвольная точка
-ось абсцисс (произвольно)
— ось ординат (перпендикулярна к оси абсцисс)
Масштаб. Виды масштабов. Точность масштаба
Рис.2.2 Линейный масштаб
По линейному масштабу расстояния измеряют с точностью 0,0 2-0,03 основания или примерно 0,5мм.
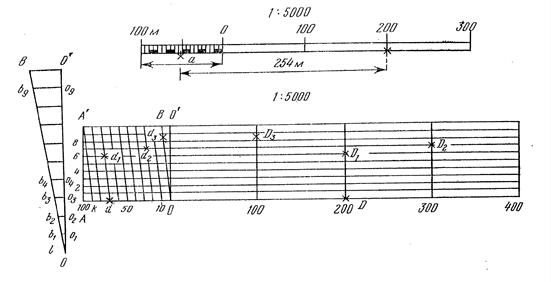
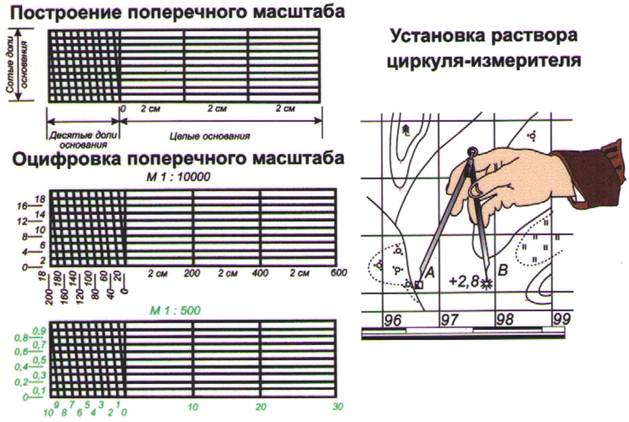
Поперечный масштаб – это график или номограмма, построенный с использованием метода пропорционального клина. Его применяют для измерений и построений на картах с повышенной точностью. Обычно его гравируют на металлических линейках или транспортирах, такие линейки называют масштабными. Он может быть построен и на чертежной бумаге. Поперечный масштаб устроен следующим образом. Он имеет вид прямоугольника, разделенного вертикальными, горизонтальными и наклонными линиями. Нижняя горизонтальная линия разделена на отрезки равные 2см, называемые основаниями масштаба, они пронумерованы: ниже линии оснований масштаба на правом краю первого основания подписан ноль, далее 1, 2, 3 и т.д., на левом краю первого основания – 1. Через концы оснований проведены перпендикуляры, которые разделены на 10 частей горизонтальными линиями с расстояниями между ними 2, 2,5 или 3мм. Нижняя и верхняя линии первого основания разделены на 10 частей. Ноль нижнего основания соединен наклонной линией с первым слева от нулевого перпендикуляра делением верхней линии, первый слева нижний со вторым слева верхним и т.д., 9-й нижний с последним (десятым) верхним. Наклонные линии называют трансверсалями. Таким образом, левая часть графика имеет вид горизонтальных и наклонных линий. Фигуры между нулевым перпендикуляром и первой к нему трансверсалью и первым слева перпендикуляром и ближайшей к нему трансверсалью имеют вид пропорционального клина. Расстояния на горизонтальных линиях между смежными трансверсалями составляют десятую долю основания, а между нулевой вертикальной линией и трансверсалями изменяется от одной сотой на первой горизонтальной линии до одной десятой доли основания на последней – верхнем основании (рис.1б). Так как первое основание разделено на десять частей и перпендикуляр к нему разделен также на десять частей, то минимальное расстояние между вертикальной и наклонной линиями клина на горизонтальной линии составляет одну сотую долю основания, поэтому такой поперечный масштаб называют сотенным. Поперечный масштаб строят в следующем порядке. На прямой линии, как и при построении линейного масштаба, откладывают несколько раз основание масштаба равное 2см. Основания нумеруют: слева от нуля 1, справа – 1, 2,3 и т.д. В конечных точках основания восстанавливают перпендикуляры длиной, равной основанию, или большей длины. Крайние перпендикуляры делят на десять частей, и через полученные точки проводят
Рис. 2.3. Линейный и поперечный масштабы
прямые линии, параллельные линии оснований. Нижнюю и верхнюю линии первого основания делят на десять равных частей. Полученные точки соединяют следующим образом: нулевую точку нижнего основания с первым верхним слева, первую нижнюю – со второй верхней и т.д. девятую нижнюю с десятой верхней, как показано на рис.1б. С помощью поперечного масштаба можно измерить длину отрезка на плане (карте) с точностью половины наименьшего деления клина, т.е. 0,1мм. Для отложения на плане измеренного на местности расстояния (горизонтального проложения), его выражают в долях основания масштаба (целых и дробных) делением на величину основания в заданном масштабе, наносят на график и с него циркулем переносят на план (карту).
Дата добавления: 2015-03-19 ; просмотров: 16758 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Поперечный масштаб
Размеры участков земной поверхности и предметов, на них расположенных, так велики, что они не могут быть изображены на бумаге без соответствующего уменьшения. Чтобы изображение местности на плане было подобно самой местности, все горизонтальные проекции линий местности изображают на плане уменьшенными в одинаковое число раз. Степень такого уменьшения называется масштабом плана.
Для повышения точности применяют поперечный масштаб, который представляет график, построенный на основании линейного масштаба.
Поперечный масштаб применяют для измерений и построений повышенной точности. Обычно поперечный масштаб гравируют на металлических пластинах, линейках, или на транспортирах, а также он может быть построен на чертеже для заданного числового масштаба.
Поперечный масштаб строят следующим образом. На прямой линии откладывают несколько раз основание масштаба равное 2 см, называемое основанием масштаба. Первое основание делят на 10 равных частей и на правом конце его пишут нуль, а на левом – то число метров или километров, которому на местности соответствует в данном масштабе основание. Вправо от нуля над каждым делением надписывают значения соответствующих расстояний на местности (рис. 19). Из каждой точки подписанного деления восставляют перпендикуляры, на которых откладывают десять отрезков, равных десятой доли основания.
Через точки, полученные на перпендикулярах, проводят прямые линии, параллельные основанию. Верхнюю линию над первым основанием делят также на десять равных частей. Полученные точки верхних и нижних делений на первом отрезке соединяют, как показано на рисунке 19. Полученные линии называются трансверсалями. Расстояние между смежными трансверсалями составляют десятую долю основания, а между нулевой вертикальной линией и смежной с ней трансверсалью – от одной сотой доли до десятой.
Рис. 19. Поперечный масштаб
Длину линии на плане берут в раствор циркуля и переносят его на нижнюю линию масштаба. Если иглы ножек циркуля точно совпадают с делениями масштаба, делают отсчет расстояния.
Если ножки циркуля не точно совпадают с делением масштаба, его перемещают вверх от одной параллели к другой, пока игла левой ножки будет точно лежать на наклонной прямой, а игла правой ножки – на вертикали справа от нуля или на нуле.
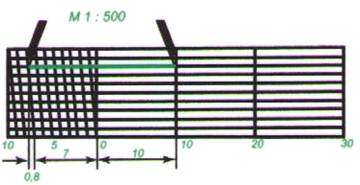
Длина отрезка на плане в мерах длины на местности (рис. 20) в масштабе 1: 500 составляет 17,8 м.
Рис. 20. Определение длин линий при помощи поперечного масштаба
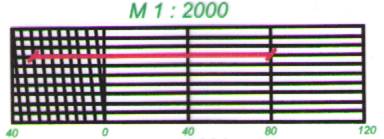
Требуется на план масштаба 1: 2000 наложить линию местности, равную 110,8 м (см. рис. 21). Рассуждаем так. Вправо от нуля до второй вертикали имеем 80 м, семь делений слева от нуля дают (7*4) 28 м; 2,8 м получим, поднимаясь вверх по наклонной прямой до седьмой горизонтали (7*0,4). Поставим на этой горизонтали иглы ножек циркуля, получим в растворе циркуля отрезок на плане, равный 110,8 м на местности. Не меняя раствора циркуля, этот отрезок и накладываем на план.
Рис. 21. Определение длин линий при помощи поперечного масштаба
При помощи поперечного масштаба можно взять отрезок с точностью 0,1 мм. Отрезок в 0,1 мм воспринимается невооруженным глазом в виде точки.
Длина линии местности, соответствующая 0,1 мм на плане, называется точностью масштаба и обозначается tm. Она зависит от численного масштаба.
Точность масштаба имеет большое практическое значение.
По точности масштаба устанавливают, при изображении каких объектов на плане можно сохранить подобие, какие объекты в данном масштабе не изображаются.
Точность масштаба 1: 25000 равна 2,5 м.
Расчет можно вести следующим образом:
В 0,1 мм – 2,5 м или tm = 0,1 мм · 25000 = 2,5 м.
Точность масштаба: определение, особенности и виды
Среди главных характеристик карт местности чаще всех выделяют данную. Это точность масштаба. В статье мы разберем, что скрывает в себе данное понятие. Также рассмотрим, что такое масштаб вообще, охарактеризуем его основные разновидности. Разберем, как понятие «графическая точность» связано с предметом нашего разговора.
Что это?
Вам будет интересно: Корпускулярная теория: понятие, автор, основные принципы и расчеты
Некоторые из этих применений, их особенности мы рассмотрим по ходу статьи.
Точность масштаба
Вам будет интересно: Распределительное свойство сложения и умножения: формулы и примеры
0,1 мм тут принят из-за того, что это наименьший отрезок, который может различить глаз человека на изображении без использования специальной техники, инструментов, приборов.
Приведем конкретный пример. Дано 1:10000. Точность масштаба станет составлять, соответственно, 1 м. Разберем подробнее:
Графическая точность
А теперь познакомимся с графической точностью масштабов. Это еще одна значимая характеристика при использовании планов и карт.
Вам будет интересно: О том, как становился современный кыргызский язык
Графическая точность связывается с разрешением «и» глаза человека. В свою очередь, оно составляет «Г». Отсюда Г=и.
То есть, если угол «и» между векторами на две точки «В» и «Л» при рассматривании их наблюдателем с нормальным уровнем зрения составляет «Г» или же более, то они будут восприниматься, как две точки. Если же данный угол к понятию разрешения меньше «Г», то «Л» и «В» будут восприниматься человеком как одна точка.
Лучше всего тут познакомиться с определением точности масштаба на конкретном примере. Допустим, человек рассматривает карту с наилучшего расстояния «б», равного 35 см. Значение Г=и. Теперь нужно определить наименьшее расстояние (то есть, графическую точность) между «В» и «Л», при котором они еще будут восприниматься наблюдателем в виде двух разных точек. Тут проводится такое вычисление:
Связь понятий
Можно вывести формулу:
Расшифруем ее элементы:
Соответственно, точность масштаба станет изменяться вместе с ним самим. Она будет тем выше, чем крупнее составитель выбрал масштаб.
А теперь разберемся с особенностями такой характеристики, как масштаб, в различных сферах применения.
Проектирование, геодезия и картография
Вам будет интересно: Одомашнивание собак: история приручения, территории, временные рамки
Разновидности графической категории
Ряд масштабов изображений в проектировании
Мы уже знаем, что означает точность масштаба 1:500. Но в каких случаях ее выбирает составитель? Разберем и этот вопрос:
В фотографии
Конечно, точность масштаба 1:10 000 более связывается с картографией. Но это применимо и для мира фотосъемки. Под масштабом здесь подразумевается отношение так называемых линейных размеров изображения, полученного на сверхчувствительной матрице или же на фотопленке, к размеру проекции соответствующей зоны проекции на плоскость, которая перпендикулярна к камере.
Есть фотографы, которые измеряют масштаб в виде отношения размеров реального объекта к его размерам на экране, фотобумаге или другом носителе. Но верный способ определения масштаба в фотографии зависит только от контекста, в котором использовано изображение.
В фотосъемке масштаб характеризуется важным значением и при расчете глубины какого-либо резко изображаемого объекта, пространства. Сегодня специалистам доступен весьма широкий выбор диапазонов масштабов от бесконечно малого (применяется при съемке далеких небесных тел) до весьма крупного (без использования специальных оптических насадок, например, сегодня возможно получить снимок масштабом 10:1).
Здесь макрофотографией считается уже съемка в масштабе 1:1 (и, соответственно, крупнее). Но с распространением цифровых компактных фотоаппаратов макросъемкой также стали называть стиль, когда объектив располагают слишком близко к объекту. Если рассматривать классическое определение, то подобное толкование не будет верным.
В моделизме
Для каждого из видов стендового (или масштабного) моделизма определены свои масштабные ряды. Они состоят из нескольких масштабов, характеризующихся определенной степенью уменьшения. Что интересно, для каждого из видов моделизма (железнодорожного, автомобильного, судомоделизма, военной техники, авиамоделизма) есть определенные исторически сформированные масштабные ряды, которые не пересекаются с иными.
Здесь масштаб исчисляется по простой формуле:
В программировании
В этой сфере будет важен так называемый масштаб времени. Разберемся, что это.
В кинотехнике
В кинотехнике тоже важна точность масштаба времени. Под последним подразумевается количественный показатель замедления либо ускорения движения, который будет равняться отношению проекционный частоты кадров к частоте съемочной.
Рассмотрим это на простом примере. Проекционная частота кадров при съемке фильма составляет 24 кадра/сек. Киносъемка производилась при этом «со скоростью» 72 кадра/сек. Масштаб времени в данном случае будет равен 1:3.
А что тогда будет означать, к примеру, 2:1? Это ускоренное в два раза по сравнению со стандартным протеканием происходящего на экране.
В математике
В этой сфере под масштабом понимается линейное соотношение двух размеров. Также во многих практически применимых областях так будет называться отношение размера изображения к реальному размеру изображаемого.
Масштабы. Точность масштаба
Карта. План. Профиль.
Конечным результатом топографо-геодезических работ являются чертежи земной поверхности, числовые данные для составления цифровых моделей местности и др. материал, представленный в упорядоченном виде. Чертежи могут быть составлены на бумажной основе, представлены в электронной форме или в виде компьютерной базы данных. Традиционными формами чертежей являются: карта, план, профиль.
При изображении на бумаге, т.е. на плоскости всей земной поверхности или значительных её участков невозможно избежать искажений изображения вследствие кривизны изображаемой поверхности, поскольку при любом способе проектирования на плоскость возникают искажения в длинах линий и углах между ними.
Уменьшенное искаженное за счёт влияния кривизны Земли, плоское изображение всей земной поверхности или значительной её части, построенное по определённым математическим законам, называется картой.
В зависимости от назначения карты при её создании выбирается определённая картографическая проекция, т.е. математический закон проектирования местности на плоскость.
Ортогональную проекцию небольших участков местности (до 20×20 км) на уровенную поверхность можно считать плоской, пренебрегая кривизной Земли. Уменьшенное изображение такой проекции на бумаге будет без искажений, вызванных кривизной Земли, и подобным участку местности.
Таким образом, уменьшенное, подобное изображение на плоскости горизонтального проложения сравнительно небольшого участка земной поверхности называется планом.
Наглядным изображением неровностей земной поверхности является профиль, т.е.уменьшенное изображение её вертикального разреза по выбранной линии.
Совокупность изображений на плане местных предметов естественного и искуственного происхождения (река, лес, кустарник, земельный участок, здание, улица и др.), называетсяситуацией местности.
Совокупность неровностей земной поверхности естественного происхождения называется рельефом местности.
Принято считать, что план можно составлять на террито рию, не превышающую площади круга радиусом 10 км.
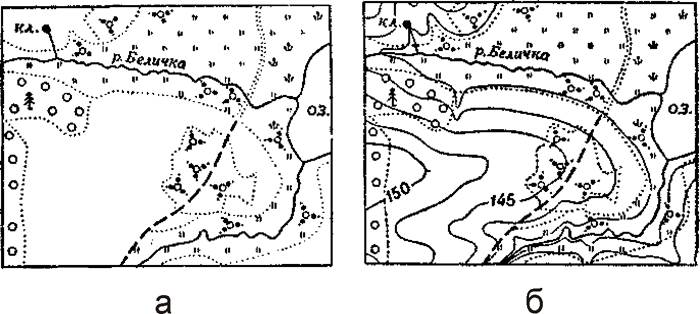
Если на плане изображены только границы объектов ме стности, его называют контурным (рис. 3.1, а). Если, кроме контуров, на план нанесен и рельеф, такой план называюттопографическим (рис. 3.1,б).
Рис.3.1. Контурный (а) и топографический (б) планы.
Картой называют чертёж, на котором может быть изображена поверхность всей Земли или любой её части в обобщенном и уменьшенном виде.
При любых измерениях по планам и картам следует помнить, что масштаб плана во всех его точках одинаковый, а масштаб во всех точках карты, как правило, различен.
| к предыдущему разделу | к следующему разделу |
Понятие о топографических планах и картах. Масштабы. Точность масштаба.
Понятие о масштабах плана и карты.
При составлении планов, карт, профилей результаты измерения линий на местности уменьшают в несколько сотен или тысяч раз.
Степень уменьшения горизонтальных проложений линий местности при изображении их на плане называется масштабом.
Под масштабом карты в общем случае понимается отношение длины линии на карте к её длине на поверхности относимости. В зависимости от картографической проекции изображения на карте в разных местах имеют различные по величине искажения, поэтому масштаб карты неодинаков. Для карт, составленных в мелком масштабе, обычно подписывается средний масштаб.
Масштаб, выраженный числом в виде простой дроби называется численным. У него числитель равен единице, а знаменатель круглое число, например, 1/500, 1/1000 или 1:500, 1:1000. Масштаб 1:500 показывает, что горизонтальное проложение линии местности уменьшено на плане в 500 раз и одной единице длины на плане, карте или профиле соответствует на местности 500 таких единиц, т.е. одному сантиметру на плане, карте или профиле соответствует 500 см или 5 м на местности.
Численный масштаб подписывают на планах, картах или профилях в их нижней части, сопровождая пояснительной надписью, например, «в 1 сантиметре 5 м», так как длины линий местности удобно выражать в метрах. Чтобы определить количество метров на местности в одном сантиметре плана (карты), надо у знаменателя численного масштаба отбросить два последних нуля, например, 1 см плана масштаба 1:2000 соответствует 20м на местности.
Планы и карты в России создаются в принятых масштабах, образующих строго определенную систему, называемую масштабным рядом. Масштабный ряд установлен с таким расчетом, чтобы он удовлетворял всем условиям потребителей и имелась возможность легко переходить от одного масштаба к другому.
Зная численный масштаб, легко длины линий местности переводить в длины линий на плане (карте) и наоборот. Такой перевод сопряжен с вычислениями, поэтому, чтобы не производить таких вычислений, пользуются шкалой (номограммой) графически построенной. Такая шкала называется линейным масштабом (рис. 3.2).
Рис. 3.2. Численный и линейный масштабы.
Линейный масштаб представляет собой график в виде отрезка прямой горизонтальной линии, на которой последовательно отложены равные отрезки, называемые основанием масштаба. Основание масштаба соответствует целому числу десятков или сотен метров на местности. Для повышения точности измерений крайнее левое основание делится на более мелкие отрезки.
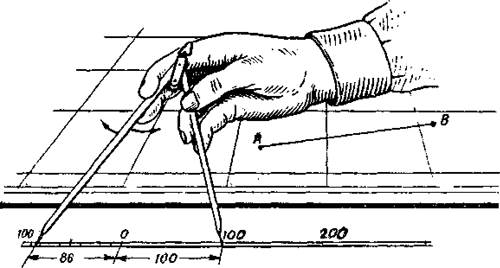
Измерения по линейному масштабу обычно производят циркулем-измерителем (рис.3.3), который перед работой должен быть хорошо отрегулирован. При измерении циркуль следует держать одной рукой, наклоняя его несколько от себя так, чтобы хорошо были видны одновременно оба острия иголок.
Рис. 3.3. Определение расстояний по линейному масштабу.
При выполнении съемочных работ мерой точности работы наряду с величиной 0,1 мм является соответствующее этой величине расстояние на местности, называемое предельной точностью масштаба. Это та максимальная точность, с которой может быть определено расстояние по данному плану (карте). При этом следует учитывать, что вследствие накопления неизбежных погрешностей в технологическом процессе изготовления плана (карты) практическая точность результата измерения расстояний по планам (картам) значительно грубее предельной графической точности и может достигать 1мм.
Предельную точность масштаба легко рассчитать, разделив знаменатель численного масштаба на 10 000. Например, точность масштаба 1:5 000 равна 0,5м. Знать величину точности масштаба необходимо при выборе масштаба съемки и при определении, какие объекты местности не следует снимать, так как они не изобразятся в данном масштабе.
Например, земельный участок размером 10×10 м на картах масштабов 1 : 50 000, 1 : 100 000 и 1 : 200 000 изобразятся в виде точки, а при масштабах плана (карты) 1 : 5000, 1 : 10 000, 1 : 25 000, будет иметь размеры соответственно 2,0×2,0 мм, 1,0×1,0мм, 0,4×0,4мм, т.е. чем больше знаменатель численного масштаба, тем детальность плана меньше и, наоборот, чем меньше знаменатель численного масштаба, тем детальность больше.
Построение поперечного масштаба, его точность. Измерение длин линий на плане.
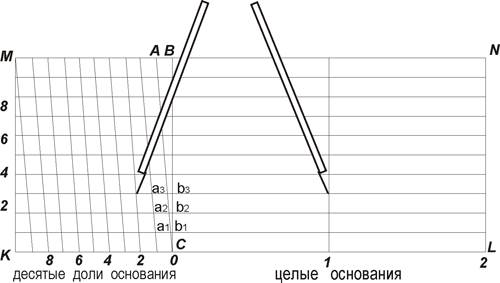
Для повышения точности измерения расстояний на плане (карте), чтобы не измерять величину отрезка «на глаз», используют шкалу поперечного масштаба, которую можно построить следующим образом.
Рис. 3.4. Нормальный поперечный масштаб.
На горизонтальной прямой КL (рис. 3.4) откладывают несколько раз основание масштаба, равное 2 см. Через полученные точки проводят линии, перпендикулярные к КL. Первое основание КС делят на десять равных частей. Крайние перпендикуляры КМ и LN делят на десять равных частей и через деления на перпендикулярах проводят линии, параллельные основаниюКL. Отрезок МВ также делят на 10 равных частей. При этом C соединяют с точкой А, а остальные наклонные линии, называемые трансверсалями, проводятся параллельно. В результате графических построений получают, так называемый, поперечный масштаб. Отрезок а1 b1 называется наименьшим делением поперечного масштаба.
Если число делений основания масштаба n, число делений на перпендикуляре m, то наименьшее деление поперечного масштаба а1 b1 будет равно:
Так как основание поперечного масштаба выбирают равным 2 см, то практически значение всех его делений в метрах можно рассчитать для любого численного масштаба.
Поперечный масштаб обычно гравируется на специальных металлических линейках, называемых масштабными, а также на геодезическом транспортире.
На таких масштабных линейках обычно указываются порядковые номера малых и больших делений, поэтому для каждого конкретного масштаба плана необходимо предварительно определить какому значению в метрах соответствует наименьшее деление масштаба и другие деления.
С помощью нормального поперечного масштаба можно откладывать и измерять расстояния с точностью до 0,2 мм, что соответствует одной сотой основания. Если же положение ножек циркуля между горизонтальными линиями шкалы оценивать на глаз, то можно отсчитывать расстояния с точностью до 0,1мм.