Что называется гидравликой и каково ее значение
Значение слова «гидравлика»
[От греч. ‛υδραυλικός — водяной]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
В отличие от гидромеханики, гидравлика характеризуется особым подходом к изучению явлений течения жидкостей: она устанавливает приближённые зависимости, ограничиваясь во многих случаях рассмотрением одноразмерного движения, широко используя при этом эксперимент, как в лабораторных, так и в натурных условиях.
Наряду с этим намечается всё большее сближение между гидромеханикой и гидравликой: с одной стороны, гидромеханика всё чаще обращается к эксперименту, с другой — методы гидравлического анализа становятся более строгими.
ГИДРА’ВЛИКА, и, мн. нет, ж. [от греч. hydōr — вода и aulos — труба]. Наука о водяных сооружениях и двигателях.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
гидра́влика
1. раздел физики, научная дисциплина, изучающая законы движения и равновесия жидкостей и их практическое применение; прикладная гидромеханика
Делаем Карту слов лучше вместе

Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: локализовать — это что-то нейтральное, положительное или отрицательное?
Гидравлика
В отличие от гидромеханики, гидравлика характеризуется особым подходом к изучению явлений течения жидкостей; она устанавливает приближённые зависимости, ограничиваясь во многих случаях рассмотрением одноразмерного движения, широко используя при этом эксперимент, как в лабораторных, так и в натурных условиях.
Наряду с этим намечается всё большее сближение между гидромеханикой и гидравликой: с одной стороны, гидромеханика всё чаще обращается к эксперименту, с другой — методы гидравлического анализа становятся более строгими. [2]
Содержание
История
Некоторые принципы гидростатики были установлены ещё Архимедом, возникновение гидродинамики также относится к античному периоду, однако формирование гидравлики как науки начинается с середины XV века, когда Леонардо да Винчи лабораторными опытами положил начало экспериментальному методу в гидравлике. В XVI—XVII веках С. Стевин, Г. Галилей и Б. Паскаль разработали основы гидростатики как науки, а Э. Торричелли дал известную формулу для скорости жидкости, вытекающей из отверстия.
В дальнейшем И. Ньютон высказал основные положения о внутреннем трении в жидкостях. В XVIII веке Д. Бернулли и Л. Эйлер разработали общие уравнения движения идеальной жидкости, послужившие основой для дальнейшего развития гидромеханики и гидравлики.
Однако применение этих уравнений (так же как и предложенных несколько позже уравнений движения вязкой жидкости) для решения практических задач привело к удовлетворительным результатам лишь в немногих случаях, в связи с этим с конца XVIII века многие учёные и инженеры (А. Шези, А. Дарси, А. Базен, Ю. Вейсбах и др.) опытным путём изучали движение воды в различных частных случаях, в результате чего наука обогатилась значительным числом эмпирических формул. Практическая гидравлика всё более отдалялась от теоретической гидродинамики. Сближение между ними наметилось лишь к концу XIX века в результате формирования новых взглядов на движение жидкости, основанных на исследовании структуры потока.
Особо заслуживают упоминания работы О. Рейнольдса, позволившие глубже проникнуть в сложный процесс течения реальной жидкости и в физическую природу гидравлических сопротивлений и положившие начало учению о турбулентном движении. Впоследствии это учение, благодаря исследованиям Л. Прандтля и Т. Кармана, завершилось созданием полуэмпирических теорий турбулентности, получивших широкое практическое применение.
К этому же периоду относятся исследования Н. Е. Жуковского, из которых для гидравлики наибольшее значение имели работы о гидравлическом ударе и о движении грунтовых вод.
В XX веке быстрый рост гидротехники, теплоэнергетики, гидромашиностроения, а также авиационной техники привёл к интенсивному развитию гидравлики, которое характеризуется синтезом теоретических и экспериментальных методов. Большой вклад в развитие науки сделали советские учёные — Н. Н. Павловский, Л. С. Лейбензон, М. А. Великанова и др.
Практическое значение гидравлики возросло в связи с потребностями современной техники в решении вопросов транспортирования жидкостей и газов различного назначения и использования их для разнообразных целей. Если ранее в гидравлике изучалась лишь одна жидкость — вода, то в современных условиях всё большее внимание уделяется изучению закономерностей движения вязких жидкостей (нефти и её продуктов), газов, неоднородных и т. н. неньютоновских жидкостей. Меняются и методы исследования и решения гидравлических задач. Сравнительно недавно в гидравлике основное место отводилось чисто эмпирическим зависимостям, справедливым только для воды и часто лишь в узких пределах изменения скоростей, температур, геометрических параметров потока; теперь всё большее значение приобретают закономерности общего порядка, действительные для всех жидкостей, отвечающие требованиям теории подобия и пр. При этом отдельные случаи могут рассматриваться как следствие обобщенных закономерностей. Постепенно гидравлика превращается в один из прикладных разделов общей науки о движении жидкостей — механики жидкости.
Предмет изучения
Гидравлика, как прикладная наука, применяется для решения различных инженерных задач в области:
Основные направления
Гидравлика обычно подразделяется на две части:
Основные разделы практической гидравлики:
Во всех указанных разделах движение жидкости рассматривается как установившееся, так и неустановившееся (нестационарное).
Основные разделы теоретической гидравлики:
Прикладное значение
Гидравлика широко использует теоретические положения механики и данные экспериментов. В прошлом гидравлика носила чисто экспериментальный и прикладной характер, в последнее время её теоретические основы получили значительное развитие, это способствовало сближению её с гидромеханикой. Гидравлика решает многочисленные инженерные задачи, рассматривает многие вопросы гидрологии, в частности, законы движения речных потоков, перемещения ими наносов, льда и шуги, процессы формирования русла и т. д. Этот комплекс вопросов объединяется речной гидравликой (динамикой русловых потоков), которую можно рассматривать как самостоятельный раздел гидравлики.
По отношению к гидромеханике гидравлика выступает как инженерное направление, получающее решение многих задач о движении жидкости на основе сочетания эмпирических зависимостей, установленных опытным путём, с теоретическими выводами гидромеханики.
В гидравлике рассматриваются также движение наносов в открытых потоках и пульпы в трубах, методы гидравлических измерений, моделирование гидравлических явлений и некоторые др. вопросы. Существенно важные для расчёта гидротехнических сооружений вопросы гидравлики — неравномерное и неустановившееся движение в открытых руслах и трубах, течение с переменным расходом, фильтрация и др. — иногда объединяют под общим названием «инженерная гидравлика», или «гидравлика сооружений».
Таким образом, круг вопросов, охватываемых гидравликой, весьма обширен, и ее законы в той или иной мере находят применение практически во всех областях инженерной деятельности, особенно в гидротехнике, мелиорации, водоснабжении, канализации, теплогазоснабжении, гидромеханизации, гидроэнергетике, водном транспорте и др.
Известные учёные-гидравлики и гидротехники
Исследования в области гидравлики координируются Международной ассоциацией гидравлических исследований (МАГИ). Её орган — «Journal of the International Association for Hydraulic Research» (Delft, с 1937).
Развитие гидравлики связано с именами учёных:
Основы гидравлики
Учебные вопросы:
Основные физические свойства жидкости.
В отличие от твердого тела жидкость характеризуется малым сцеплением между частицами, вследствие чего она обладает текучестью и принимает форму сосуда, в который ее помещают.
Жидкости подразделяют на два вида:
Капельные жидкости обладают большим сопротивлением сжатию (практически несжимаемы) и малым сопротивлением касательным и растягивающим усилиям (из-за незначительного сцепления частиц и малых сил трения между частицами).
К капельным жидкостям относятся вода, бензин, керосин, нефть, ртуть и другие
Газообразные жидкости характеризуются почти полным отсутствием сопротивления сжатию.К газообразным жидкостям относятся все газы.
К основным физическим свойствам жидкости относятся:
Плотность — это отношение массы к объему, занимаемому этой массой. Плотность измеряют в системе СИ в килограммах на кубический метр (кг/м3). Плотность воды составляет 1000 кг/м3.
Используются также укрупненные показатели: – килопаскаль — 1 кПа= 103 Па; – мегапаскаль — 1 МПа = 106 Па.
Сжимаемость жидкости — это ее свойство изменять объем при изменении давления. Это свойство характеризуется коэффициентом объемного сжатия или сжимаемости, выражающим относительное уменьшение объема жидкости при увеличении давления на единицу площади. Для расчетов в области строительной гидравлики воду считают несжимаемой. В связи с этим при решении практических задач сжимаемостью жидкости обычно пренебрегают.
Величина, обратная коэффициенту объемного сжатия, называется модулем упругости. Модуль упругости измеряется в паскалях
Температурное расширение жидкости при ее нагревании характеризуется коэффициентом температурного расширения, который показывает относительное увеличение объема жидкости при изменении температуры на 1 С.
В отличие от других тел объем воды при ее нагревании от 0 до 4 °С уменьшается. При 4 °С вода имеет наибольшую плотность и наибольший удельный вес; при дальнейшем нагревании ее объем увеличивается. Однако в расчетах многих сооружений при незначительных изменениях температуры воды и давления изменением этого коэффициента можно пренебречь.
Вязкость жидкости — ее свойство оказывать сопротивление относительному движению (сдвигу) частиц жидкости. Силы, возникающие в результате скольжения слоев жидкости, называют силами внутреннего трения, или силами вязкости.
Силы вязкости проявляются при движении реальной жидкости. Если жидкость находится в покое, то вязкость ее может быть принята равной нулю. С увеличением температуры вязкость жидкости быстро уменьшается; остается почти постоянной при изменении давления.
Гидростатика
Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практическое применение.
В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением.
Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна.
Гидростатическое давление обладает свойствами
Основное уравнение гидростатики
Рассмотрим распространенный случай равновесия жидкости, когда на нее действует только одна массовая сила – сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке рассматриваемого объема жидкости. Это уравнение называется основным уравнением гидростатики.
Запишем сумму сил, действующих на рассматриваемый объем в проекции на вертикальную ось:
Последний член уравнения представляет собой вес жидкости, заключенный в рассматриваемом вертикальном цилиндре объемом hdS. Силы давления по боковой поверхности цилиндра в уравнение не входят, т.к. они перпендикулярны к этой поверхности и их проекции на вертикальную ось равны нулю. Сократив выражение на dS и перегруппировав члены, найдем:
Полученное уравнение называют основным уравнением гидростатики. По нему можно посчитать давление в любой точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления P0 на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости.
Пьезометрический и гидростатический напоры
Рассмотрим закрытый сосуд с жидкостью, к которому в точках А и В на произвольной глубине присоединены пьезометры I и II (рис. 9).
Давление на свободной поверхности в сосуде больше атмосферного. Трубка I сверху открыта и давление на свободной поверхности в ней равно атмосферному. Трубка II сверху запаяна, из нее удален воздух, т.е. давление в ней равно нулю.
Для определения вертикальных координат точек А и В проведем на произвольной высоте горизонтальную плоскость 0-0. Эта плоскость называется плоскостью сравнения. Вертикальное расстояние от плоскости сравнения до рассматриваемой точки называется геометрической высотой точки по отношению к плоскости сравнения и обозначается буквой. За плоскость сравнения может быть принят уровень земли, пола.
Так как давление в сосуде на свободной поверхности жидкости больше атмосферного, то в пьезометрических трубках I и II жидкость поднимется на большую высоту, чем уровень жидкости в сосуде. Обозначим высоту поднятия жидкости в открытом пьезометре через – пьезометрическая высота, а высоту поднятия жидкости в закрытом пьезометре через – приведенная высота.
Сумма геометрической высоты и пьезометрической для любой точки жидкости будет величиной постоянной и называется пьезометрическим напором:
Подставив это выражение в формулу (1) получим:
это сумма приведенной высоты и геометрической высоты положения, называемая гидростатическим напором Hs.
В уравнении (5) Hs=const для любой точки жидкости, а не 
Поэтому, сколько бы мы пьезометров не подключили, во всех пьезометрах жидкость установится на одном уровне: плоскость, соответствующая уровню П–П, называется пьезометрической плоскостью, а уровню Н–Н – напорной плоскостью.
Удельная потенциальная энергия, т.е. энергия приходящаяся на единицу веса частицы будет соответственно равна:
Аналогично, гидростатический напор Hs является также мерой удельной потенциальной энергии жидкости, но большей по сравнению Hp на величину удельной потенциальной энергии атмосферного давления.
Вакуум. Закон Паскаля.
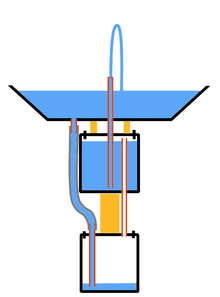
Вакуум — пространство, свободное от вещества. В технике и прикладной физике под вакуумом понимают среду, содержащую газ при давлении значительно ниже атмосферного. Вакуум характеризуется соотношением между длиной свободного падения молекул газа λ и характерным размером среды d. Под d может приниматься расстояние между стенками вакуумной камеры, диаметр вакуумного трубопровода и т. д. В зависимости от величины соотношения λ/d различают низкий, средний и высокий вакуум.
Насос для демонстрации вакуума
Законом Паскаля в гидростатике называется следующее утверждение,сформулированное французским учёным Блезом Паскалем: давление, производимое на жидкость или газ, передается в любую точку без изменений во всех направлениях.
На основе закона Паскаля работают различные гидравлические устройства: тормозные системы, гидравлические процессы и др.
В законе Паскаля речь идет не о давлениях в разных точках гидравлической системы, а о возмущениях давления в разных точках, поэтому закон справедлив и для жидкости в поле силы тяжести.
В случае движущейся несжимаемой жидкости можно условно говорить о справедливости закона Паскаля, ибо добавление произвольной постоянной величины к давлению не меняет вида уравнения движения жидкости, однако в этом случае термин закон Паскаля обычно не применяется. Для сжимаемых жидкостей (газов) закон Паскаля, вообще говоря, несправедлив.
Виды движения жидкости
Виды движения жидкости бывают:
Примерами неустановившегося движения являются опорожнение резервуаров, водохранилищ, движение воды в реках при переменном уровне (при паводках, сбросах воды через плотину) и т. д.
сброс воды через плотину
Установившимся – наз. движение жидкости неизменное во времени, при котором давление и скорость являются функциями только координат, но не зависит от времени. u = f1(x, y, z); p = f2(x, y, z).
Установившееся движение подразделяется на:
Равномерное движение характеризуется постоянством параметров по длине потока. Примерами такого движения являются движения в трубах постоянного сечения и в каналах правильной формы. Поле линий тока равномерного движения – семейство параллельных прямых.
В зависимости от причин, вызывающих движение, и условий, в которых оно происходит, различают:
Напорное движение происходит в потоке, со всех сторон ограниченном твердыми стенками. Давление во всех точках потока отлично от атмосферного и может быть как больше, так и меньше последнего. Движение происходит под действием разности давлений по длине потока, которая может быть создана водонапорной башней, питающим баком, насосной установкой.
Безнапорное движение происходит под действием силы тяжести при наличии свободной поверхности жидкости. Примерами безнапорного движения является движение в реках, каналах и трубах, когда сечение последних не полностью заполнено жидкостью.
Гидродинамика
Предметом изучения гидродинамики является движущаяся жидкость. Как было указано ранее, все без исключения физические и химические процессы, которые составляют основу промышленных технологических процессов, происходят в динамических условиях, в условиях движения текучих сред.
При движении жидкостей под воздействием внешних сил в потоках прежде всего формируются поля скоростей микро- и макрочастиц, которые определяют формирование температурных и полей концентраций веществ, что в конечном итоге обусловливает скорость протекания процессов.
На движущуюся жидкость, кроме сил, которые действовали на покоящуюся жидкость (поверхностные силы гидростатического давления и массовые силы: силы тяжести и внешние силы инерции), действуют дополнительные силы инерции и силы трения. В отличие от гидростатического давления, величина которого не зависит от ориентации поверхности, на которое оно действует, возникающее при движении гидродинамическое давление благодаря развитию напряжениям сдвига (касательным силам), различно в направлении осей X, Y и Z.
Наличие сил внутреннего трения между движущимися частицами жидкости (в соответствии с законом внутреннего трения Ньютона) является первопричиной различия скоростей движения в различных точках по поперечному сечению канала. Характер этого различия, который обусловливается характером связи между давлением и скоростью движения частиц в любой точке потока. Это и является основной задачей теории гидродинамики.
Уравнение неразрывности потока.
Уравнение неразрывности потока отражает закон сохранения массы: количество втекающей жидкости равно количеству вытекающей. Например, на рис. 15 расходы во входном и выходном сечениях напорной трубы равны: q1 = q2.
Схема к уравнению неразрывности потока.
С учётом, что q = Vw, получим уравнение неразрывности потока:
Если отсюда выразим скорость для выходного сечения:
то легко заметить, что она увеличивается обратно пропорционально площади живого сечения потока. Такая обратная зависимость между скоростью и площадью является важным следствием уравнения неразрывности и применяется в технике, например, при тушении пожара для получения сильной и дальнобойной струи воды.
Ламинарный и турбулентный режим движения жидкости.
Наблюдения показывают, что в природе существует два разных движения жидкости:
От чего зависит характер движения жидкости, установил Рейнольдс в 1883 году путем. Эксперименты показали, что переход от ламинарного к турбулентному движению происходит при определенной скорости (критическая скорость), которая для труб различных диаметров неодинакова: при увеличении диаметра она увеличивается, критическая скорость так же увеличивается при увеличении вязкости жидкости. Рейнольдс вывел общие условия существования ламинарного и турбулентных режимов движения жидкости. По Рейнольдсу режима движения жидкости зависят от безразмерного числа, которое учитывает основные, определяющие это движение: среднюю скорость, диаметр трубы, плотность жидкости и ее абсолютную вязкость.
Это число называется числом Рейнольдса:
При числе Рейнольдса 


При переходе от ламинарного режима движения жидкости к турбулентному критическое значение 
Уравнение Бернулли.
Закон (уравнение) Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:
p — плотность жидкости,
h— высота, на которой находится рассматриваемый элемент жидкости,
p— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,
g— ускорение свободного падения.
Константа в правой части часто называется полным давлением и зависит, в общем случае, от линии тока.
Соотношение, близкое к приведенному выше, было получено в 1739 г. Даниилом Бернулли, с именем которого обычно связывают интеграл Бернулли. В современном виде интеграл был получен Иоганном Бернулли около 1740 года.
Bernoulli Johann 1667-1748
СВОЙСТВА ГАЗОВ И ЖИДКОСТЕЙ
Список литературы:
1. В.П. Гусев «Основы гидравлики», Томск, 2009 г.
2. Бретшнайдер С. «Свойства газов и жидкостей», Москва