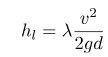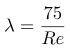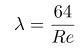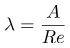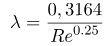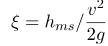Что называется гидравлическим сопротивлением

Гидравлическое сопротивление

Гидравлическое сопротивление или гидравлические потери – это суммарные потери при движении жидкости по водопроводящим каналам. Их условно можно разделить на две категории:

Потери трения – возникают при движении жидкости в трубах, каналах или проточной части насоса.

Потери на вихреобразование – возникают при обтекании потоком жидкости различных элементов. Например, внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п. Такие потери принято называть местными гидравлическими сопротивлениями.

Содержание статьи

Коэффициент гидравлического сопротивления

Гидравлические потери выражают либо в потерях напора Δh в линейных единицах столба среды, либо в единицах давления ΔP:

где ρ — плотность среды, g — ускорение свободного падения.

В производственной практике перемещение жидкости в потоках связано с необходимостью преодолеть гидравлическое сопротивление трубы по длине потока, а также различные местные сопротивления:
Поворотов
Диафрагм
Задвижек
Вентилей
Кранов
Различных ответвлений и тому подобного

На преодоление местных сопротивлений затрачивается определенная часть энергии потока, которую часто называют потерей напора на местные сопротивления. Обычно эти потери выражают в долях скоростного напора, соответствующего средней скорости жидкости в трубопроводе до или после местного сопротивления.

Аналитически потери напора на местные гидравлические сопротивления выражаются в виде.

где ξ – коэффициент местного сопротивления (обычно определяется опытным путем).

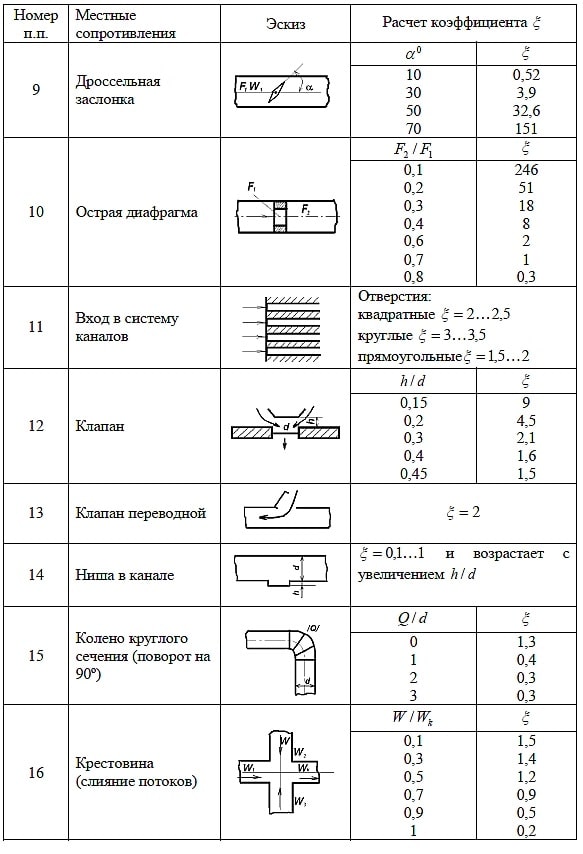
Данные о значении коэффициентов различных местных сопротивлений приводятся в соответствующих справочниках, учебниках и различных пособиях по гидравлике в виде отдельных значений коэффициента гидравлического сопротивления, таблиц, эмпирических формул, диаграмм и т.д.

Исследование потерь энергии (потери напора насоса), обусловленных различными местными сопротивлениями, ведутся уже более ста лет. В результате экспериментальных исследований, проведенных в России и за рубежом в различное время, получено огромное количество данных, относящихся к разнообразнейшим местным сопротивлениям для конкретных задач. Что же касается теоретических исследований, то им пока поддаются только некоторые местные сопротивления.

В этой статье будут рассмотрены некоторые характерные местные сопротивления, часто встречающиеся на практике.

Местные гидравлические сопротивления

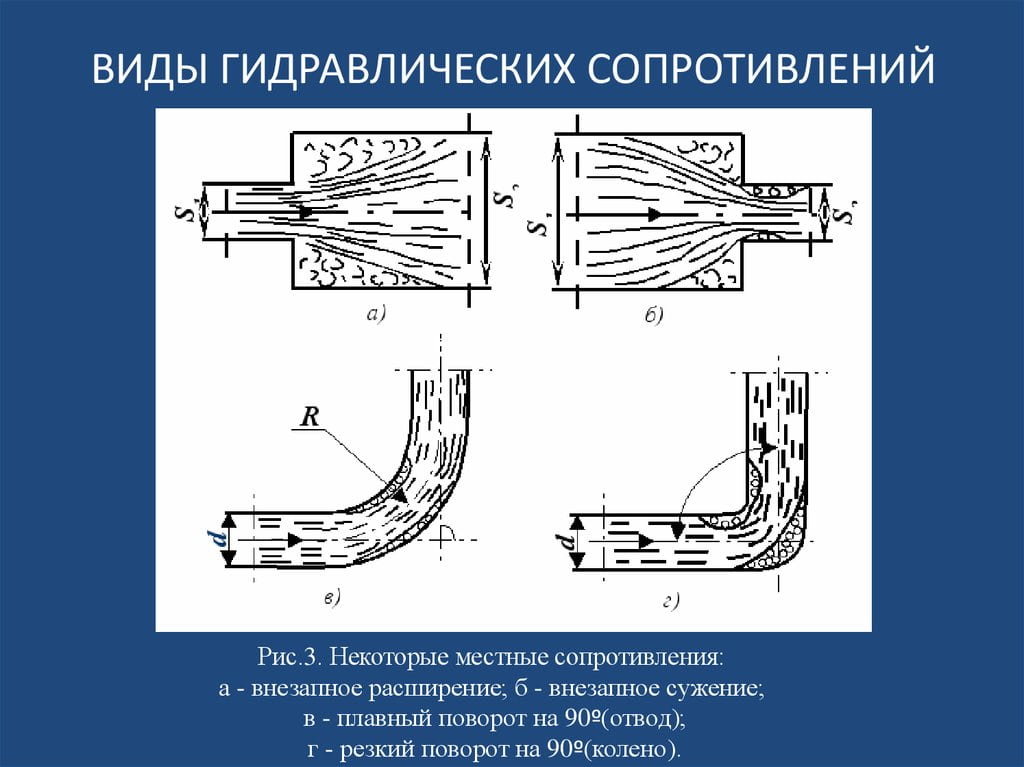
Как уже было написано выше, потери напора во многих случаях определяются опытным путем. При этом любое местное сопротивление похоже на сопротивление при внезапном расширении струи. Для этого имеется достаточно оснований, если учесть, что поведение потока в момент преодоления им любого местного сопротивления связано с расширением или сужением сечения.

Гидравлические потери на внезапное сужение трубы

Сопротивление при внезапном сужении трубы сопровождается образованием в месте сужения водоворотной области и уменьшения струи до размеров меньших, чем сечение малой трубы. Пройдя участок сужения, струя расширяется до размеров внутреннего сечения трубопровода. Значение коэффициента местного сопротивления при внезапном сужении трубы можно определить по формуле.

Значение коэффициента ξ_{вн. суж} от значения отношения (F₂/F₁)) можно найти в соответствующем справочнике по гидравлике.

Гидравлические потери при изменении направления трубопровода под некоторым углом

В этом случае вначале происходит сжатие, а затем расширение струи вследствие того, что в месте поворота поток по инерции как бы отжимается от стенок трубопровода. Коэффициент местного сопротивления в этом случае определяется по справочным таблицам или по формуле

ξ _{поворот} = 0,946sin(α/2) + 2.047sin(α/2) 2

где α – угол поворота трубопровода.

Местные гидравлические сопротивления при входе в трубу

В частном случае вход в трубу может иметь острую или закругленную кромку входа. Труба, в которую входит жидкость, может быть расположена под некоторым углом α к горизонтали. Наконец, в сечении входа может стоять диафрагма, сужающая сечение. Но для всех этих случаев характерно начальное сжатие струи, а затем её расширение. Таким образом и местное сопротивление при входе в трубу может быть сведено к внезапному расширению струи.

Если жидкость входит в цилиндрическую трубу с острой кромкой входа и труба наклонена к горизонту под углом α, то величину коэффициента местного сопротивления можно определить по формуле Вейсбаха:

ξ_вх = 0,505 + 0,303sin α + 0,223 sin α 2

Местные гидравлические сопротивления задвижки

На практике часто встречается задача расчета местных сопротивлений, создаваемых запорной арматурой, например, задвижками, вентилями, дросселями, кранами, клапанами и т.д. В этих случаях проточная часть, образуемая разными запорными приспособлениями, может иметь совершенно различные геометрические формы, но гидравлическая сущность течения при преодолении этих сопротивлений одинакова.

Гидравлическое сопротивление полностью открытой запорной арматуры равно

ξ_{вентиля} = от 2,9 до 4,5

Величины коэффициентов местных гидравлических сопротивлений для каждого вида запорной арматуры можно определить по справочникам.

Гидравлические потери диафрагмы

Процессы, происходящие в запорных устройствах, во многом похожи на процессы при истечении жидкости через диафрагмы, установленные в трубе. В этом случае также происходит сужение струи и последующее её расширение. Степень сужения и расширения струи зависит от ряда условий:
режима движения жидкости
отношения диаметров отверстия диафрагмы и трубы
конструктивных особенностей диафрагмы.

Для диафрагмы с острыми краями:

Местные гидравлические сопротивления при входе струи под уровень жидкости

Преодоление местного сопротивления при входе струи под уровень жидкости в достаточно большой резервуар или в среду, не заполненную жидкостью, связано с потерей кинетической энергии. Следовательно, коэффициент сопротивления в этом случае равен единице.

Видео о гидравлическом сопротивлении

На преодоление гидравлических потерь затрачивается работа различных устройств (насосов и гидравлических машин)

Для снижения влияния гидравлических потерь рекомендуется в конструкции трассы избегать использования узлов способствующих резким изменениям направления потока и стараться применять в конструкции тела обтекаемой формы.

Даже применяя абсолютно гладкие трубы приходится сталкиваться с потерями: при ламинарном режиме течения(по Рейнольдсу) шероховатость стенок не оказывает большого влияния, но при переходе к турбулентному режиму течения как правило возрастает и гидравлическое сопротивление трубы.

Источник

Гидравлическое сопротивление труб

Гидравлическое сопротивление – это сопротивление движению потока рабочей среды, которое оказывается со стороны трубопроводной системы и оценивается количеством потерянной удельной энергии, безвозвратно расходуемой на работу сил трения. При этом гидропотери могут возникать в результате:

Расчет гидравлического сопротивления и его роль

Любая трубопроводная коммуникация имеет не только прямолинейные участки, но и повороты, ответвления, для создания которых используются различные фитинги. А для регулирования потока рабочей среды устанавливается запорная арматура. Всё это создаёт сопротивление, поэтому очень важно перед тем, как приступать к монтажу трубопровода, необходимо выполнить ряд расчётов, в том числе определить гидравлическое сопротивление. Это позволит в будущем сократить теплопотери и, соответственно, избежать лишних энергозатрат.

Гидравлический расчёт выполняется с целью:

Во время движения по замкнутому контуру рабочему потоку приходится преодолевать определённое гидравлическое сопротивление. Причём с увеличением его значения, должна увеличиваться мощность насоса. Только правильные расчёты помогут выбрать оптимальный вариант насоса. Нет смысла покупать слишком мощное оборудования для трубопроводов с низким гидравлическим сопротивлением, ведь, чем больше мощность, тем выше энергозатраты.

А если мощность будет, наоборот, недостаточной, то насосное оборудование не сможет обеспечить достаточный напор теплоносителя, что приведёт к увеличению тепловых потерь.

Коэффициент гидравлического сопротивления трубы

Это безмерная величина, показывающая, каковы потери удельной энергии.

Ламинарное перемещение рабочего потока

При ламинарном (равномерном) перемещении рабочей среды по трубопроводу круглого сечения потери давления по длине вычисляется по формуле Дарси-Вейсбаха:

— потери давления по длине;

— коэффициент гидравлического сопротивления;

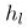
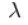
v – скорость движения рабочей среды;

g – ускорение силы тяжести;

d – диаметр трубопроводной магистрали.

Практически определено, что на коэффициент гидравлического сопротивления непосредственное влияние оказывает число Рейнольдса (Re) – безмерная величина, которая характеризует поток жидкости и выражается отношением динамического давления к касательному напряжению.

Если Re меньше, чем 2300, то для расчёта применяется формула:

Для трубопроводов в форме круглого цилиндра:

Для трубопроводных коммуникаций с другим (не круглым) сечением:

Где А=57 – для квадратных труб.

Турбулентное течение рабочего потока

При турбулентном (неравномерном, беспорядочном) перемещении рабочего потока коэффициент сопротивления вычисляют опытным путём, как функцию от Re. Если необходимо определить коэффициент гидравлического сопротивления для магистрали круглого сечения с гладкими поверхностями при

, то для расчёта применяется формула Блаузиуса:

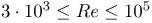
В случае турбулентного перемещения рабочей среды на величину коэффициента трения влияет число Рейнольдса (характер течения) и насколько гладкая внутренняя поверхность трубопроводной коммуникации.

Коэффициент местного сопротивления

Это безмерная величина, которая устанавливается экспериментальным путём с помощью формулы:

– коэффициент местного сопротивления;

– потеря напора;

– отношение скорости потока к ускорению силы тяжести – скоростной поток.

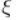
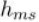
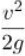
При неизменной скорости перемещения рабочей среды по всему сечению применяется формула:

, где

– энергия торможения.

Источник

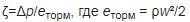
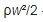
Гидравлическое сопротивление

Выполнение расчета гидравлического сопротивления отдельного трубопровода и всей системы в комплексе является ключевой задачей в гидравлике, решение которой позволяет подобрать сечения труб и насос с необходимыми значениями давления и расхода в рабочем режиме.

В одной из ранних статей на блоге рассмотрен простой пример расчета трубопровода с параллельными участками с использованием понятия «характеристика сопротивления». В конце статьи я анонсировал: «Можно существенно повысить точность метода…». Под этой фразой подразумевалось учесть зависимость характеристик сопротивления от расхода более точно. В том расчете характеристики сопротивлений выбирались из таблиц по диаметру трубы и по предполагаемому расходу. Полковов Вячеслав Леонидович написал взамен таблиц пользовательские функции в Excel для более точного вычисления гидравлических сопротивлений, которые любезно предоставил для печати. Термины «характеристика сопротивления» и «гидравлическое сопротивление» обозначают одно и то же.

Краткая теория.

В упомянутой выше статье теория вкратце рассматривалась. Освежим в памяти основные моменты.

Движение жидкостей по трубам и каналам сопровождается потерей давления, которая складывается из потерь на трение по длине трубопровода и потерь в местных сопротивлениях – в изгибах, отводах, сужениях, тройниках, запорной арматуре и других элементах.

В гидравлике в общем случае потери давления вычисляются по формуле Вейсбаха:

∆Р=ζ·ρ·w²/2, Па, где:

Если с плотностью и скоростью всё более или менее понятно, то определение коэффициентов местных сопротивлений – достаточно непростая задача!

Как было отмечено выше, в гидравлических расчетах принято разделять два вида потерь давления в сетях трубопроводов.

∆Р_тр=ζ_тр·ρ·w²/2=λ·L·ρ·w²/(2·D), Па, где:

Таким образом, при учете сопротивления трению коэффициент потерь – коэффициент местного сопротивления – и коэффициент гидравлического трения связаны для круглых труб зависимостью:

ζ_тр=λ·L/D

Коэффициенты местных сопротивлений определяются для каждого вида «препятствия» по индивидуальным эмпирическим формулам, полученным из практических опытов.

Выполним ряд математических преобразований. Для начала выразим скорость потока через массовый расход жидкости:

w=G/(ρ·π·D²/4), м/с, где:

∆Р_тр=8·λ·L·G²/(ρ·π²·D 5 ), Па;

Введем понятие гидравлических сопротивлений:

S_тр=8·λ·L·/(ρ·π²·D 5 ), Па/(кг/с)²;

S_м=8·ζ_м·/(ρ·π²·D 4 ), Па/(кг/с)².

И получим удобные простые формулы для вычисления потерь давления при прохождении жидкости в количестве G через эти гидравлические сопротивления:

Размерность гидравлического сопротивления (Па/(кг/с)²) определена массовой скоростью (кг/с) движения жидкости, а физические процессы в транспортных системах зависят от её объёмной скорости (м 3 /с), что учтено в формулах присутствием объёмной плотности ρ транспортируемой жидкости.

Для последовательного и параллельного соединений гидравлических сопротивлений справедливы формулы:

S_пар=1/(а₁+a₂+…+a_n)², Па/(кг/с)²;

Коэффициент гидравлического трения.

Для определения гидравлического сопротивления от трения о стенки трубы S_тр необходимо знать параметр Дарси λ – коэффициент гидравлического трения по длине.

В технической литературе приводится значительное количество формул разных авторов, по которым выполняется вычисление коэффициента гидравлического трения в различных диапазонах значений числа Рейнольдса.

Обозначения в таблице:

В [1] приведена еще одна интересная формула расчета коэффициента гидравлического трения:

λ=0,11·[(68/Re+k/D+(1904/Re) 14 )/(115·(1904/Re) 10 +1)] 0,25

Вячеслав Леонидович выполнил проверочные расчеты и выявил, что вышеприведенная формула является наиболее универсальной в широком диапазоне чисел Рейнольдса!

Значения, полученные по этой формуле чрезвычайно близки значениям:

Расчет в Excel гидравлических сопротивлений.

Для облегчения выполнения рутинных гидравлических расчетов Полковов В.Л. разработал ряд пользовательских функций. Перечень некоторых из них, наиболее часто используемых на практике, приведен в таблице ниже.

Некоторые пояснения по аргументам пользовательских функций:

Приведённые пользовательские функции желательно использовать с учётом начального участка транспортирования (расстояния от одного гидравлического сопротивления до следующего гидравлического сопротивления). Это позволяет уменьшить погрешности расчётов, вызванных влиянием «неустановившегося» характера потока жидкости.

Для турбулентных течений длина начального участка должна быть не менее:

L_нач=(7,88·lg (Re) – 4,35)·D

Для ламинарных течений минимальная длина начального участка:

Здесь В=0,029 по данным Буссинекса, и В=0,065 по данным Шиллера, D — внутренний диаметр системы транспортирования.

Далее на скриншоте показана таблица в Excel с примерами расчетов гидравлических сопротивлений.

Литература:

Ссылка на скачивание файла: gidravlicheskie-soprotivleniya (xls 502,0KB).

Источник

Гидравлическое сопротивление: виды и коэффициенты

Местные гидравлические сопротивления — зачастую причина кавитации. Как рассчитывать коэффициенты разных сопротивлений? Какова зависимость между сопротивлениями и кавитацией?

Одно из основных понятий в гидравлике — гидравлические потери (сопротивление). Речь идет о потерях, которые наблюдаются при движении жидкости по водопроводящим каналам.

Условно гидравлические потери можно разделить на две группы:

Исследования потерь энергии потока (потерь напора насосов), обусловленных местными сопротивлениями, проводятся уже не одно десятилетие. В разное время в России и за рубежом проводились различные экспериментальные исследования, которые позволили получить множество данных относительно разных местных сопротивлений. В теории ученые продвинулись не так далеко: до сих пор не удается создать универсальные формулы, которые можно было бы применять с любыми типами локальных сопротивлений, — пока речь идет о некоторых местных сопротивлениях.

Коэффициент гидравлического сопротивления: что это такое и как высчитывается

Выражаться гидравлические потери могут по-разному — в единицах давления или линейных единицах столба жидкости, потерях напора.

Общая формула потери напора выглядит так:

где △P — потери в единицах давления,

p — плотность среды,

g — ускорение свободного падения.

В сфере промышленности, в производственной практике перемещение жидкостей в потоках неразрывно связано с необходимостью преодоления гидравлического сопротивления трубы по всему пути потока. Кроме этого, гидравлические потери обуславливаются местным сопротивлением встречающихся на пути ответвлений и кранов, задвижек и вентилей, поворотов и диафрагм.

Чтобы преодолевать местные сопротивления, поток затрачивает определенную часть энергии — в этом случае речь идет о потере напора на локальные сопротивления. Как правило, такие потери выражают в долях от скоростного напора, который соответствует средней скорости среды в трубах до местного сопротивления либо после него.

Найти данные о коэффициентах разных местных сопротивлений можно в соответствующих учебниках, пособиях, справочниках по гидравлике — данные могут быть представлены в разном виде, например как отдельные значения коэффициента гидравлических потерь, в виде диаграмм, таблиц, эмпирических формул.

При желании или необходимости потери напора на локальные гидравлические сопротивления можно рассчитать самостоятельно. Для этого используется формула:

где ξ представляет собой коэффициент местного сопротивления. Как правило, его определяют опытным путем,

g — ускорение свободного падения.

Местные гидравлические сопротивления: свойства и характеристики

Как мы уже упоминали, потери напора жидкости в случае с местными сопротивлениями определяются в большинстве случаев только опытным путем. Но и в теоретическом обосновании есть некоторые прорывы — так, местное сопротивление по своим свойствам и характеристикам аналогично сопротивлению, которое наблюдается при внезапном расширении струи. И это логично, если учитывать, что поведение потока жидкости при преодолении любого локального сопротивления сопровождается сужением или расширением сечения.

2. При изменении направления трубы под углом гидравлические потери рассчитываются по формуле: ξ поворот = 0,946sin(α/2) + 2,047sin(α/2)², где α — это угол поворота трубы. Поток ведет себя следующим образом: сначала струя сжимается, после чего расширяется, так как при повороте по инерции поток отжимается от стенок трубы.

3. При входе в трубу цилиндрической формы с острой кромкой, которая наклонена к горизонту под углом α, коэффициент местного сопротивления высчитывается по формуле Вейсбаха: ξвх = 0,505 + 0,303sin α + 0,223sin α². Иногда труба имеет закругленную форму или в сечении входа стоит диафрагма, которая сужает сечение, — в любом случае сначала струя потока будет сжиматься, потом расширяться, то есть местное сопротивление при входе в водопровод можно свести к внезапному расширению струи потока.

4. В промышленности, в частности при работе с насосным оборудованием, часто приходится рассчитывать местные сопротивления, которые создаются запорной арматурой — вентилями и клапанами, кранами и задвижками и так далее. Вне зависимости от того, какую геометрическую форму имеет проточная часть, ограниченная запорной арматурой, гидравлический характер течения при преодолении сопротивлений не меняется. Если мы говорим о полностью открытой запорной арматуре, гидравлическое сопротивление будет колебаться в диапазоне от 2,9 до 4,5. Коэффициенты для определенного вида запорной арматуры можно найти в соответствующих справочниках.

5. Гидравлические потери диафрагмы определяются сужением струи потока и последующим ее расширением. Степень сужения потока и его последующего расширения определяется несколькими факторами — это особенности конструкции диафрагмы, отношение диаметров отверстия трубы и диафрагмы, режим движения жидкости и так далее.

6. Наконец, часто бывает необходимо рассчитать коэффициент местного сопротивления при входе струи потока под уровень жидкости. Впрочем, сложных расчетов проводить не потребуется, коэффициент сопротивления при входе струи в большой резервуар под уровень жидкости или в среду без жидкости связан с потерей кинетической энергии и равен 1.

О гидравлическом сопротивлении, насосах и кавитации

Работа насосов и гидравлических машин направлена в том числе на преодоление гидравлических потерь. Чтобы снизить влияние таких потерь, при создании трассы стоит избегать узлов, которые будут резко менять направления потока. Оптимальный вариант — конструкции обтекаемой формы. Но нужно понимать, что даже максимально гладкие трубы не обеспечат отсутствие потерь: ламинарный режим течения не сопровождается большими потерями из-за шероховатых стенок, но турбулентный режим приводит и к росту гидравлического сопротивления трубы.

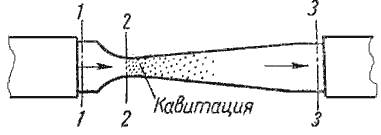
Иногда при движении жидкости по закрытым руслам меняется ее агрегатное состояние — она превращается в пар, то есть из жидкости выделяются газы, в ней растворенные. Если скорость небольшая, видимых изменений в ее движении не будет. Но при увеличении скорости движения на узком участке трубы появится отчетливая зона с пузырьками газа. Далее, когда жидкость подходит к широкой части трубы, пузырьки начинают резко уменьшаться в размерах, а затем исчезать — схлопываться. В месте схлопывания пузырьков резко увеличивается давление, которое затем передается на соседние объемы среды и далее на стенки трубы. Многочисленные местные повышения давлений приводят к вибрации.

Кавитация — нежелательное явление, которое может привести к очень быстрому износу определенных частей трубопроводного и насосного оборудования. Часто она возникает в местах локальных сопротивлений — в вентилях, кранах, задвижках и так далее. При этом кавитация снижает КПД, а в долгосрочной перспективе разрушает детали, стенки трубопроводов, уменьшая их пропускную способность.

Источник