Что называется геодезической широтой
АСТРОНОМИЧЕСКАЯ СИСТЕМА КООРДИНАТ
ГЕОДЕЗИЧЕСКАЯ СИСТЕМА КООРДИНАТ
Геодезическими координатами называются угловые величины (широта и долгота), определяющие положение точек (объектов) на поверхности земного эллипсоида (референц-эллипсоида) относительно плоскости экватора и начального меридиана.
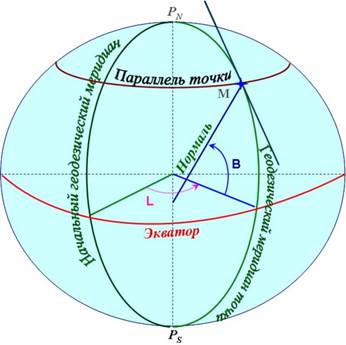
Геодезической широтой (В) называется угол, заключенный между плоскостью экватора и нормалью к поверхности земного эллипсоида, проходящей через данную точку.
Рис. 3.1. Геодезическая система координат
Счет геодезических широт ведется от 0 до 90° к северу и к югу от экватора. Геодезические широты Северного полушария называются северными и имеют знак « + », а Южного — южными и имеют знак «—». Геодезическая широта измеряется центральным углом в плоскости меридиана.
Геодезическая широта (в градусах) показывает, насколько данная точка на земном эллипсоиде расположена севернее или южнее плоскости экватора.
Геодезическая широта для точек, расположенных на экваторе, будет равна 0°, а для точек, расположенных на полюсах ± 90°.
Геодезической долготой (L) называется двугранный угол, заключенный между плоскостью начального меридиана и плоскостью геодезического меридиана, проходящего через данную точку.
В старину в отдельных государствах заначальныймеридиан принимали меридиан, проходящий через свою главную обсерваторию. В настоящее время в Украине и в большинстве стран мира для единообразия в определении долгот условились начальным считать Гринвичский меридиан, проходящий через астрономическую обсерваторию в Гринвиче (близ Лондона). От этого меридиана ведется счет так называемого международного гринвичского времени.
Геодезическая долгота измеряется либо центральным углом в плоскости экватора или параллели, либо дугой экватора от начального (Гринвичского) меридиана до меридиана, проходящего через данную точку (М), в пределах от 0 до 180° к востоку или к западу. Геодезические долготы для точек, расположенных к востоку от меридиана Гринвича до 180°, называются восточными и считаются положительными, а к западу – западными и считаются отрицательными.
Восточная долгота обозначается буквами (в.д.) или знаком « + », западная долгота — буквами (з.д.) или знаком « – ».
Геодезическая система координат, отнесенная к эллипсоиду Красовского, была разработана в 1942 – 1943 годах, поэтому она получила название системы координат 1942 года. Вместе с ней была принята Балтийская система высот, по которой ведется отсчет абсолютных высот относительно нуля Кронштадтского футштока (Футшток — специальная рейка с делениями).
АСТРОНОМИЧЕСКАЯ СИСТЕМА КООРДИНАТ
Астрономические координаты определяют положение точки на поверхности геоида. Их можно получить путем астрономических измерений с помощью геодезических инструментов или путем математической обработки результатов геодезических измерений.
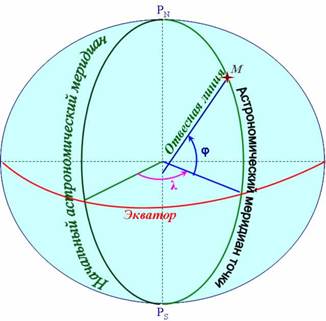
Астрономической широтой (φ) называется угол, заключенный между плоскостью земного экватора и направлением отвесной линии в данной точке.
Астрономическая широта измеряется от 0 до 90° к северу и к югу от экватора. В Северном полушарии астрономические широты называются северными, а в Южном — южными.
Отвесная линия в общем случае не совпадает с направлением нормали к поверхности земного эллипсоида. Поскольку различные по плотности массы в теле Земли распределены неравномерно, то отклонение отвесной линии (силы тяжести) от нормали различное в разных точках Земли. Так, например, в районе Кавказа отклонения отвесных линий от нормалей достигают 35″, а разность отклонений отвесных линий на противоположных берегах озера Байкал достигает 40″. В среднем величина отклонений равна 4 – 5″ (рис. 3.2).
Рис. 3.2. Астрономическая система координат
Астрономической долготой (λ) называется двугранный угол, заключенный между плоскостью начального астрономического меридиана и плоскостью астрономического меридиана, проходящего через данную точку.
Поскольку плоскость астрономического меридиана проходит через отвесную линию в данной точке на поверхности Земли, а плоскость геодезического меридиана проходит через нормаль к поверхности эллипсоида, следовательно, плоскости астрономического и геодезического меридианов не совпадают. В результате этого геодезическая широта, долгота и геодезический азимут в данной точке отличаются от астрономической широты, долготы, и астрономического (истинного) азимута. Эти расхождения будут увеличиваться там, где наблюдаются большие отклонения отвесной линии от нормали, а также в тех точках геоида, где его поверхность дальше удалена от поверхности эллипсоида.
Геодезическая и астрономическая системы координат различаются как две отдельные системы при определении местоположения объектов с точностью до 1″ (в линейной величине до 20 – 30 м). Зная астрономические координаты, можно вычислить геодезические координаты путем ввода поправок на уклонение отвесных линий от нормалей, определяемых астрономо-геодезическим методом или по специальным гравиметрическим картам.
Геодезические координаты
Смотреть что такое «Геодезические координаты» в других словарях:
Геодезические координаты — см. в ст. Координаты. Горная энциклопедия. М.: Советская энциклопедия. Под редакцией Е. А. Козловского. 1984 1991 … Геологическая энциклопедия
ГЕОДЕЗИЧЕСКИЕ КООРДИНАТЫ — широта и долгота точки земной поверхности, определенные путем геодезических измерений расстояния и направления от точки с известными географическими координатами, и высота точки относительно т. н. референц эллипсоида (см. Красовского эллипсоид) … Большой Энциклопедический словарь
геодезические координаты — Три величины, две из которых характеризуют направление нормали к поверхности земного эллипсоида в данной точке пространства относительно плоскостей его экватора и начального меридиана, а третья является высотой точки над поверхностью земного… … Справочник технического переводчика
геодезические координаты — Широта и долгота точки земной поверхности, определенные путем геодезических измерений расстояния и направления от точки с известными географическими координатами, а также высота точки относительно поверхности земного эллипсоида … Словарь по географии
геодезические координаты — широта и долгота точки земной поверхности, определённые путём геодезических измерений расстояния и направления от точки с известными географическими координатами, и высота точки относительно так называемого референц эллипсоида (см Красовского… … Энциклопедический словарь
геодезические координаты — geodezinės koordinatės statusas T sritis fizika atitikmenys: angl. geodesic coordinates; geodetic coordinates vok. geodätische Koordinaten, f rus. геодезические координаты, f pranc. coordonnées géodésiques, f … Fizikos terminų žodynas
Геодезические координаты — СИСТЕМЫ КООРДИНАТ 23. Геодезические координаты D. Geodatische Koordinaten E. Geodetic coordinates F. Coordonnées géodésiques Три величины, две из которых характеризуют направление нормали к поверхности земного эллипсоида в данной точке… … Словарь-справочник терминов нормативно-технической документации
ГЕОДЕЗИЧЕСКИЕ КООРДИНАТЫ — широта и долгота точки земной поверхности, определённые путём геод. измерений расстояния и направления от точки с известными геогр. координатами, и высота точки относительно т. н. референц эллипсоида (см. Красовского эллипсоид) … Естествознание. Энциклопедический словарь
Плоские прямоугольные геодезические координаты — 10. Плоские прямоугольные геодезические координаты Плоские прямоугольные координаты По ГОСТ 22268 76 Источник: ГОСТ 19156 79: Аппаратура навигационная наземная одометрическая. Термины и определения … Словарь-справочник терминов нормативно-технической документации
Геодезическая широта
Источник:
(утв. Приказом Ростехрегулирования от 28.09.2006 N 215-ст)
Смотреть что такое «Геодезическая широта» в других словарях:
геодезическая широта — Угол, образованный нормалью к поверхности земного эллипсоида в данной точке и плоскостью его экватора. [ГОСТ 22268 76] Тематики геодезия Обобщающие термины системы координат EN geodetic latitude DE geodätische Breite FR latitude géodésique … Справочник технического переводчика
Геодезическая широта — 25. Геодезическая широта D. Geodätische Breite Е. Geodetic latitude F. Latitude géodésique Угол, образованный нормалью к поверхности земного эллипсоида в данной точке и плоскостью его экватора Источник: ГОСТ 22268 76: Геодезия. Термины и… … Словарь-справочник терминов нормативно-технической документации
геодезическая широта В — 3.11 геодезическая широта В: Острый угол, образованный нормалью к поверхности эллипсоида в данной точке и плоскостью экватора, положительный по направлению к северу и отрицательный к югу. Источник: ГОСТ Р 52572 2006: Географические информационные … Словарь-справочник терминов нормативно-технической документации
геодезическая — [картографическая] производственная деятельность вид геодезической [картографической] деятельности, основное содержание которой составляют геодезические [картосоставительские, картоиздательские] процессы; Источник: ГКИНП 17 004 99: Инструкци … Словарь-справочник терминов нормативно-технической документации
широта — ы/, мн. о/ты, о/т, м. 1) разг. Протяжение чего л. в поперечнике. Широта улицы. Широта стены. Покровская слобода против Саратова, на другом берегу Волги; только широта реки мешает назвать эту слободу предместьем города (Чернышевский). Синонимы:… … Популярный словарь русского языка
Геодезическая астрономия — раздел практической астрономии (См. Практическая астрономия), наиболее тесно связанный с геодезией и картографией; изучает теорию и методы определения широты φ и долготы λ места, а также азимута а направления на земной предмет и местного… … Большая советская энциклопедия
Широта — одна из координат в ряде систем сферических координат, определяющих положение точек на земной поверхности (см. Географические координаты, Координаты в геодезии), на небесной сфере (см. Небесные координаты), на поверхности Солнца, Луны,… … Большая советская энциклопедия
ГОСТ 22268-76: Геодезия. Термины и определения — Терминология ГОСТ 22268 76: Геодезия. Термины и определения оригинал документа: 114. Абрис Ндп. Кроки D. Gelandeskizze Gelandekroki E. Outline Field sketch F. Croquis Схематический чертеж участка местности Определения термина из разных документов … Словарь-справочник терминов нормативно-технической документации
ГОСТ Р 52572-2006: Географические информационные системы. Координатная основа. Общие требования — Терминология ГОСТ Р 52572 2006: Географические информационные системы. Координатная основа. Общие требования оригинал документа: 3.1 абсцисса X: Линейное расстояние в системе координат картографической сетки от отсчетной линии восток запад, к… … Словарь-справочник терминов нормативно-технической документации
Аномалия силы тяжести — Разность между измеренным значением силы тяжести g и ее нормальным (теоретическим) значением y, т.е. g y. Измерения силы тяжести производят на физической поверхности Земли. Нормальное значение получают с использованием нормальной формулы силы… … Энциклопедия РВСН
Тема 1.3. Системы координат, применяемые в геодезии



Для определения положения точек в геодезии применяют пространственные прямоугольные, геодезические и плоские прямоугольные координаты.
Пространственные прямоугольные координаты. Начало системы координат расположено в центре O земного эллипсоида (рис. 2.2).
Геодезические координаты. Геодезическими координатами точки являются ее широта, долгота и высота (рис. 2.2).
Геодезической широтой точки М называется угол В, образованный нормалью к поверхности эллипсоида, проходящей через данную точку, и плоскостью экватора.
Плоскости сечения эллипсоида, проходящие через ось OZ, называются геодезическими меридианами.
Геодезической долготой точки М называется двугранный угол L, образованный плоскостями начального (гринвичского) геодезического меридиана и геодезического меридиана данной точки.
Долготы отсчитывают от начального меридиана в пределах от 0° до 360° на восток, или от 0° до 180° на восток (положительные) и от 0° до 180° на запад (отрицательные).
Геодезической высотой точки М является ее высота Н над поверхностью земного эллипсоида.
Геодезические координаты с пространственными прямоугольными координатами связаны формулами
Геодезические и пространственные прямоугольные координаты точек определяют с помощью спутниковых измерений, а также путем их привязки геодезическими измерениями к точкам с известными координатами.
Астрономические координаты отличаются от геодезических потому, что направления отвесных линий не совпадают с направлениями нормалей к поверхности эллипсоида. Угол между направлением нормали к поверхности эллипсоида и отвесной линией в данной точке земной поверхности называется уклонением отвесной линии.
Обобщением геодезических и астрономических координат является термин – географические координаты.
Плоские прямоугольные координаты. Для решения задач инженерной геодезии от пространственных и геодезических координат переходят к более простым – плоским координатам, позволяющим изображать местность на плоскости и определять положение точек двумя координатами х и у.
Поскольку выпуклую поверхность Земли изобразить на плоскости без искажений нельзя, введение плоских координат возможно только на ограниченных участках, где искажения так малы, что ими можно пренебречь. В России принята система прямоугольных координат, основой которой является равноугольная поперечно–цилиндрическая проекция Гаусса. Поверхность эллипсоида изображается на плоскости по частям, называемым зонами. Зоны представляют собой сферические двуугольники, ограниченные меридианами, и простирающиеся от северного полюса до южного (рис. 2.3). Размер зоны по долготе равен 6°. Центральный меридиан каждой зоны называется осевым. Нумерация зон идет от Гринвича к востоку.
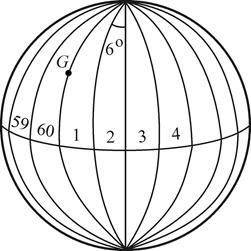 | Рис. 2.3. Деление поверхности Земли на координатные зоны: G – Гринвич |
Долгота осевого меридиана зоны с номером N равна:
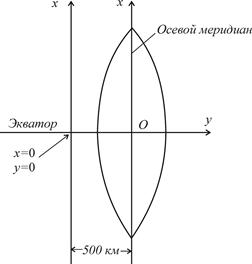 | Рис. 2.4. Изображение координатной зоны на плоскости: О – начало координат (х0=0; у0=500 км). |
Чтобы избежать отрицательных значений ординат, координаты пересечения принимают равными x0 = 0, y0 = 500 км, что равносильно смещению оси х к западу на 500 км.
Чтобы по прямоугольным координатам точки можно было судить, в какой зоне она расположена, к ординате y слева приписывают номер координатной зоны.
Пусть например, координаты точки А имеют вид:
Эти координаты указывают на то, что точка А находится на расстоянии 6276427 м от экватора, в западной части (y
Географические и геодезические координаты
Географические координаты ввел во II в. до н. э. греческий ученый Гиппарх. Земля представлялась в то время как однородный шар.
Географическими координатами являются угловые величины, называемые широтой и долготой, определяющие положение точки земной поверхности относительно экватора и начального меридиана.
Плоскость экватора проходит через центр Земли и перпендикулярна к ее оси вращения. В качестве начального меридиана избран меридиан, проходящий через Гринвичскую обсерваторию (Англия). Однако сама Гринвичская обсерватория в настоящее время не функционирует и сохраняется лишь как историческое место. Следует заметить, что на почетную роль начального меридиана в разное время претендовали Пулковский, Парижский, Лиссабонский и другие меридианы. Плоскость любого меридиана проходит через ось вращения Земли.
Географическая долгота – двугранный угол (l) между плоскостью начального меридиана и плоскостью меридиана, проходящего через данную точку, измеряемый в экваториальной плоскости (рис. 2, а) вправо и влево от начального меридиана, т. е. долгота бывает восточная (+) и западная (-) от 0 до 180°.
Географическая широта – угол (j) между радиусом шара, т. е. отвесной линией проходящей через данную точку, и плоскостью экватора. Широта на экваторе равна 0, на полюсах: северном +90°, на южном –90°.
Координаты, получаемые из непосредственных полевых наблюдений светил, стали называть астрономическими.
Астрономическая широта (jА) – угол, образованный отвесной линией в данной точке и плоскостью, перпендикулярной к оси вращения Земли.
Астрономическая долгота (lА) – двугранный угол между плоскостями астрономических меридианов данной точки и начального меридиана. Астрономический меридиан образуется сечением земной поверхности плоскостью, проходящей через отвесную линию в данной точке параллельно оси вращения Земли.
Рис. 2. Системы координат. Определение координат точки А:
а – географической долготы (l) и широты (j) на шаре;
б – в эллипсоидальной (В, L, Н = АА0) и
пространственной системах координат (ХА, YA, ZA)
Системы координат, применяемые в современной геодезии, можно разделить на две группы: эллипсоидальные, определяющие положение точки на поверхности эллипсоида; прямоугольные (двухмерные на плоскости, трехмерные в пространстве). К эллипсоидальным относятся геодезические координаты.
Геодезическая широта (В) – угол между нормалью к поверхности эллипсоида в данной точке и плоскостью экватора (рис. 2, б).
Геодезическая долгота (L) – двугранный угол между плоскостями геодезического меридиана (на поверхности эллипсоида) данной точки и начального меридиана.
В настоящее время географические координаты рассматриваются как обобщенное понятие об астрономических и геодезических координатах, когда уклонения отвеса от нормали к эллипсоиду не учитываются.
Геодезическую систему координат, связанную с общеземным эллипсоидом, распространенную на всю планету и предназначенную для решения научных и практических задач на планетарном или региональном уровнях, называют общеземной системой.
На поверхности Земли координатные системы закрепляют пункты геодезических сетей, которые являются их составной частью. Поэтому из-за неравномерности размещения геодезических пунктов, погрешностей измерений, особенностей их математической обработки общеземные системы координат различаются между собой.
Геодезическую систему координат, связанную с референц-эллипсоидом, распространяемую в пределах материка или территории того или иного государства, называют референцной системой.
Геодезические системы координат включают:
высоту геоида над эллипсоидом в начальном пункте;
исходные геодезические даты (геодезические широта и долгота начального пункта, азимут с начального пункта на ориентирный пункт геодезической сети).
В работах по геодезии, картографии и топографии, выполняемых в СССР и затем в России, с 1946 г. принят эллипсоид Красовского (начальный пункт Пулково; превышение геоида над референц-эллипсоидом в начальном пункте равно нулю).
Размеры эллипсоида Красовского довольно близки к размерам общеземного эллипсоида, а их сжатия практически совпадают.
Эллипсоид Красовского в качестве координатной поверхности вместе с выбранными исходными геодезическими датами (координатами начального пункта геодезической сети страны и азимутом исходной стороны) образует государственную референцную «Систему координат 1942 г.» (СК-42).
В настоящее время Государственными системами геодезических координат и высот России являются система координат 1995 г. (СК-95), введенная постановлением Правительства РФ с 1 июля 2002 г., и Балтийская система высот. В качестве координатной поверхности в этой системе используется эллипсоид Красовского. За начало координат (как и в СК-42) приняты координаты центра Пулковской астрономической обсерватории, за исходный уровень отсчета высот – средний многолетний уровень Балтийского моря с исходным пунктом нивелирной сети в Кронштадте.
Положение пунктов в принятой системе координат может задаваться следующими координатами:
пространственными прямоугольными координатами X, Y, Z (направление оси Z совпадает с осью вращения отсчетного эллипсоида, ось X лежит в плоскости нулевого меридиана, а ось Y дополняет систему до правой; началом системы координат является центр отсчетного эллипсоида);
геодезическими координатами: широтой – В, долготой – L, высотой – Н. Геодезическая высота Н отсчитывается от точки на земной поверхности по нормали до поверхности эллипсоида;
плоскими прямоугольными координатами х и у, вычисляемыми в проекции Гаусса–Крюгера. Третья координата – абсолютная высота измеряется от среднего уровня Балтийского моря.
Астрономические долготы и широты, обозначаемые соответственно буквами jА и lА, получаются из прямых полевых наблюдений небесных светил, а геодезические обозначаются буквами В и L и связаны с размерами и ориентированием конкретного референц-эллипсоида в теле Земли и могут быть только вычислены. Началом координат в геодезической системе (на референц-эллипсоиде) служит точка ориентирования эллипсоида с известными астрономическими координатами (у нас в стране – это сигнал «А», т. е. центр круглого зала Пулковской обсерватории).
Геодезические координаты относятся к нормали к поверхности эллипсоида, а географические – к отвесной линии, т. е. нормали к уровенной поверхности, или к геоиду. Отвесная линия, нормаль к эллипсоиду и радиус-вектор эллипсоида, проведенные через одну и ту же точку на поверхности эллипсоида, занимают разные положения в пространстве.
Угол между отвесной линией и нормалью к поверхности эллипсоида называют уклонением отвесной линии, оно составляет от 2 – 3″ до 30 – 40″ и более в аномальных районах. Угол в 1″ на поверхности Земли соответствует дуге в 30 м. Из-за этого различия в астрономических и геодезических координатах могут колебаться от сотни метров в среднем до километра и более в аномальных районах. Поэтому для перехода от астрономических широт и долгот к геодезическим необходимо определять в разных пунктах Земли уклонения отвесных линий. Учет этих различий при расчетах обязателен для всех топографических карт. Игнорировать их можно только при мелкомасштабном картографировании.
В настоящее время в спутниковой геодезии применяются две общеземные системы координат: Всемирная геодезическая система WGS-84 и Российская система ПЗ-90 (Параметры Земли).
В системе WGS-84 начало отсчета координат задано в центре масс Земли; ось Z пространственной прямоугольной системы координат параллельна направлению на условный земной полюс (Международное условное начало МУН); ось X определяется плоскостями условного меридиана (параллелен нулевому меридиану) и экватора; ось Y дополняет систему координат до правой. Начало и положение осей этой координатной системы совпадает с геометрическим центром и осями общеземного эллипсоида WGS-84 с параметрами: а = 6 378 137 м,
a = 1:298,257 223 563, е 2 = 0,006 694 380.
Система координат WGS-84, полученная в США по данным наблюдений ИСЗ, в дальнейшем неоднократно уточнялась, и с 1994 г. используется версия WGS-84 (G 730).
Система координат ПЗ-90 также является геоцентрической прямоугольной пространственной системой с началом в центре масс Земли; ось Z направлена к условному земному полюсу, а ось X – в точку пересечения плоскости экватора и нулевого меридиана. Полученные в результате модернизации геодезические параметры Земли относятся к 2002 г., поэтому новой системе дано обозначение ПЗ-90 (2002). Параметры эллипсоида в этой системе следующие: а = 6 378 136 м, a = 1:298,257 839 303, е 2 = 0,006 694 6619.
Системы координат WGS-84 и ПЗ-90 весьма близки друг к другу. Так, например, размеры больших полуосей эллипсоидов различаются на 1 м.