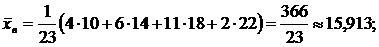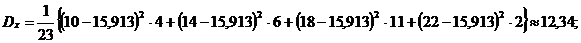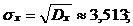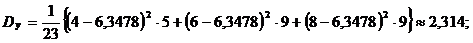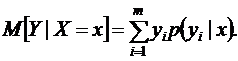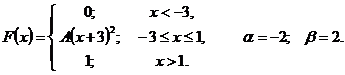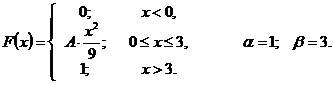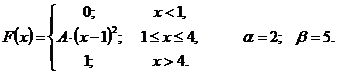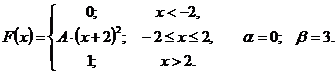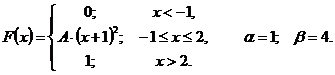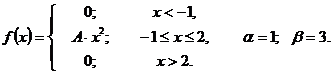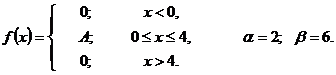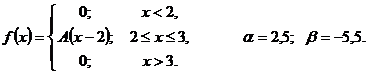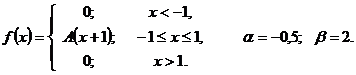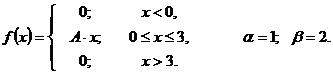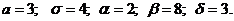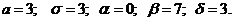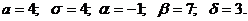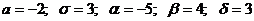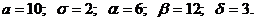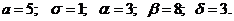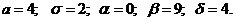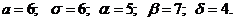Что называется функцией распределения интегральным законом распределения случайной величины х
Содержание:
Законы распределения:
Распределение случайных переменных: Каждая из случайных переменных имеет ряд возможных значений, могущих возникнуть с определенной вероятностью.
Случайные переменные величины могут носить прерывный (дискретный) и непрерывный характер. Возможные значения прерывной случайной переменной отделены друг от друга конечными интервалами. Возможные значения непрерывной случайной переменной не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток.
Примерами прерывных случайных переменных могут служить:
Примеры непрерывных случайных переменных:
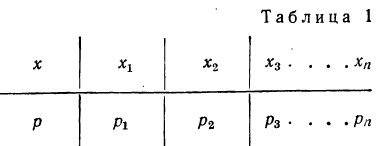
Если перечислить все возможные значения случайной переменной и указать вероятности этих значений, то получится распределение случайной переменной. Распределение случайной переменной указывает на соотношение между отдельными значениями случайной величины и их вероятностями.
Распределение случайной переменной будет задано законом распределения, если точно указать, какой вероятностью обладает каждое значение случайной переменной.
Такая таблица называется также рядом распределения случайной переменной.
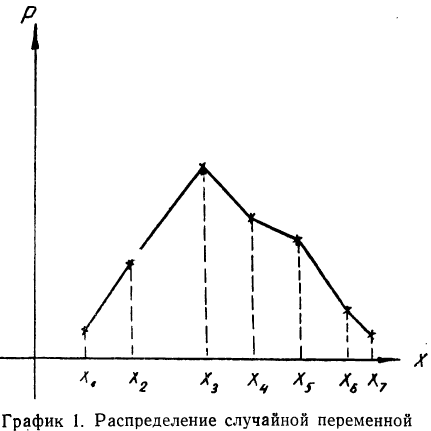
Для наглядности ряд распределения изображают графически, откладывая на прямоугольной системе координат по оси абсцисс возможные значения случайной переменной, а по оси ординат — их вероятности. В результате графического изображения получается многоугольник или полигон распределения (график 1). Многоугольник распределения является одной из форм закона распределения.
Функция распределения
Ряд распределения является исчерпывающей характеристикой прерывной случайной перемен-
Вероятность того, что Х
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Интегральная функция распределения случайной величины и её свойства. Функция распределения дискретной случайно величины
Задание случайной величины её законом распределения не обладает общностью, так как его нельзя использовать, например, для непрерывных случайных величин. Кроме того, даже для дискретных случайных величин закон распределения не удовлетворяет практическим требованиям. Например, с точки зрения практики событие, состоящие в том, что некоторый прибор проработает, например, 1000 часов, не представляет интереса. Более важным является событие Х 1000. Такое событие имеет вероятность, отличную от нуля, и при изменении Х вероятность события 
Следовательно, вероятность 
Определение 4. Интегральной функцией распределения вероятностей случайной величины Х называется функция F(х), соответствующая вероятности того, что в результате опыта случайная величина Х примет значение меньшее х – некоторого значения случайной величины.
Таким образом, по определению
F(x) = Р(X x
Таким образом, функция F(х) здесь составная (ступенчатая) и она претерпевает разрыв 1-го рода в точках хk и скачки этой функций равны pk = = Р(Х = хk) (k = 1, 2, 3, 4, 5, 6) (рисунок 3.5). Заметим, что функция распределе-ния для непрерывной случайной величины имеет форму плавной кривой (рисунок 3.6).
Интегральная функция распределения вероятностей случайной величины



ТЗР-3. Интегральная функция распределения вероятностей СВ
Интегральная функция распределения вероятностей представляет собой вероятность того, что некоторая случайная величина Х принимает значение меньшее, чем текущее х:
| Оценка Х | |||||
| Вероятность | 0,1 | 0,5 | 0,3 | 0,1 | — |
| Функция распределения F(х) | 0,1 | 0,6 | 0,9 | 1,0 |
Для нахождения значений функции распределения необходимо воспользоваться её определением (20):
· для Х = 2 F(2)= Р(Х
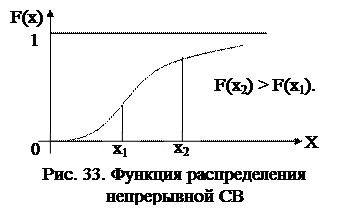
Для того чтобы понять, как будет выглядеть график интегральной функции распределения для непрерывной СВ, можно прибегнуть к следующим рассуждениям. Если представить, что количество значений дискретной СВ возрастает, то мест разрыва будет становиться больше, а высота ступенек будет уменьшаться. В пределе, когда количество возможных значений станет бесконечным (а это и есть непрерывная СВ), ступенчатый график превратится в непрерывный (рис. 30).
Поскольку интегральная функция распределения вероятностей СВ имеет первостепенное значение, рассмотрим подробнее ее свойства:
Свойство 1. Такой способ задания закона распределения универсален, т. к. пригоден для задания закона распределения как дискретных, так и непрерывных СВ.
Свойство 2. Поскольку интегральная функция распределения – это вероятность, то ее значения лежат на отрезке от 0 до 1.
Свойство 3. Функция распределения безразмерна, как и любая вероятность.
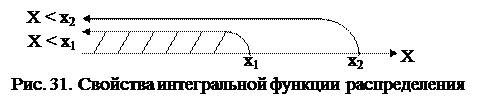


Следствие 1
Вероятность того, что величина Х примет значение в интервале (х1;х2) равна разности значений интегральной функции на границах интервала:
Функция распределения, или интегральный закон распределения
Его числовые характеристики:
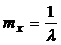
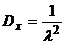

Случайная величина Х распределена по нормальному закону, если ее плотность вероятности имеет вид:
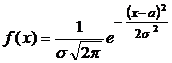
где а, σ – параметры, вероятностный смысл которых: а – математическое ожидание; σ – среднее квадратическое отклонение Х.
Вероятность того, что Х примет значение, принадлежащее интервалу (α, β), равна:
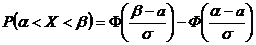
где 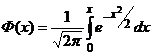
Вероятность того, что абсолютная величина отклонения случайной величины Х от математического ожидания меньше положительного числа δ, равна:
Величины хi называются вариантами вариационного ряда; величина n
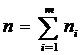
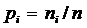
2. При большом значении n для упрощения статистической обработки выборки вариационный ряд разбивается на интервалы одинаковой длины, в каждый из которых попадают варианты с близкими значениями. Длина интервала hx находится по формуле Стерджеса:
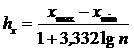
где хmin и хmax – минимальное и максимальное значения вариант в выборке, а в качестве hx удобно брать целое четное число, ближайшее к значению правой части в (2.3).
За начало первого интервала принимается значение хнач.= хmin– hx/2. Конец последнего интервала хкон. должен удовлетворять условию хкон. – hx ≤ хmax ≤ хкон.. Варианта, попадающая на границу интервалов, включается в оба интервала с весом 0,5.
Можно также руководствоваться и другим правилом, например, включать в интервал варианту, совпадающую с началом интервала, а варианту, совпадающую с концом, не включать в интервал, либо наоборот. Важно лишь придерживаться выбранного правила и при заполнении корреляционной таблицы. Полученное представление выборки называется интервальным рядом распределения Х.
При интервальном распределении, помимо hx, вводятся также следующие характеристики: 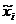
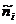
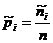
— относительная частота для i-го интервала.
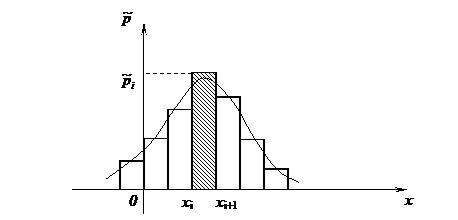
3. Для графического представления интервального ряда используется гистограмма, представляющая собой совокупность 
4. Модой М0 интервального распределения случайной величины называется середина интервала с максимальной относительной частотой (на рис. 6 это интервал, соответствующий заштрихованному прямоугольнику).
Медианой Ме выборки называется значение срединного элемента вариационного ряда. Для интервального распределения при четном числе интервалов медианой является граница двух срединных интервалов, а при нечетном числе интервалов – середина срединного интервала (на рис. 6 медианой является середина заштрихованного интервала).
5. Выборка величины Х может быть охарактеризована статистическим параметрами: средним, дисперсией, среднимквадратическимотклонением, которые вычисляются соответственно по формулам:
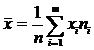
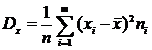
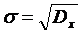
Аналогичные величины для интервального распределения случайной величины Х вычисляются по формулам:
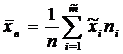
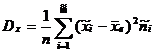
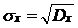
Величины 
6. Пусть для параметра а из опыта получена несмещенная оценка ã. Находится такое значение ε, для которого вероятность теоретического распределения равна Р(|ã – a| 2 (Приложение 3) находится критическое значение 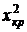
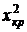
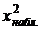
9. Связь между случайными величинами Х и Y может носить случайный характер. В этом случае говорят о статистической связи Х и Y.
Если среднее значение Х (Y) функционально зависит от значений Y, то говорят о корреляционной связи Х и Y.
Для выяснения вопроса о том, существует ли корреляция между Х и Y, интервальный ряд записывается в виде корреляционной таблицы 1.
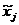 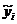 | ny |
| nx | n = 23 |
В первой строке последовательно записываются значения середин интервалов 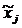
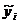
На пересечении i-й строки и j-го столбца записывается частота nxy, равная числу вариант из Х, попавших в j-й интервал интервального распределения Х, при одновременном попадании в i-й интервал интервального распределения Y nxy вариант из Y. В случае nxy = 0 в соответствующей клетке таблицы ставится ноль. В последней строке записываются суммы всех nxy при данных значениях 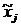

В клетке, расположенной в нижнем правом углу таблицы, записывается сумма всех частот n = ∑nx = ∑ny.
10. Если в корреляционной таблице в основном заполнены клетки вблизи одной или другой диагонали (как в таблице 1), то стоит искать линейную связь между Х и Y.
Если заполненное большинство клеток таблицы образует какую-то кривую, то искать линейную связь между Х и Y не имеет смысла.
Выборочный коэффициент корреляции rв характеризует степень корреляции (связи) между Х и Y и изменяется в пределах 0 ≤ | rв | ≤ 1. При rв = 0 корреляция между Х и Y отсутствует, а при | rв | = 1 корреляция между Х и Y переходит в функциональную связь.
В предположении линейной корреляции между Х и Y rв рассчитывается по формуле
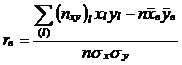
где 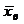
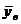
В качестве примера найдем rв из данных таблицы 1:
По формуле (2.21) находим rв:
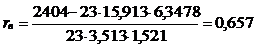
Можно сделать вывод, что между Х и Y имеется заметная корреляция.
11. Условным математическим ожиданием дискретной случайной величины Y при Х=х, где х – определенное значение случайной величины Х, называется произведение возможных значений Y на их условные вероятности:
Как видно из формулы, условное математическое ожидание M[Y | x] является функцией от х:
которую называют функцией регрессии Y на Х.
Аналогично определяется условное математическое ожидание дискретной случайной величины Х и функция регрессии Х на Y:
Величины M[Y | x] и M[Х | у] обозначаются, собственно как 
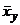
Уравнения 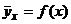
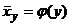
В случае линейной корреляции между Х и Y эти линии будут прямыми и определяются уравнениями:

Задания на контрольную работу № 5
1. В книге 150 страниц. Какова вероятность того, что порядковый номер наудачу открытой страницы будет : а) оканчиваться цифрой 3; б) число кратное 5; в) число 25?
2. Чему равна вероятность того, что наудачу выбранные последовательно 4 цифры: 1) не содержат цифру 0; 2) все различны; 3) образуют четырехзначное число?
4. Номер телефона состоит из 7 цифр. Какова вероятность того, что все цифры наугад набранного номера различные?
5. Слово «планета» составлено из букв разрезной азбуки. Карточки с отдельными буквами тщательно перемешаны. Какова вероятность того, что: а) разложив в ряд, получим слово «крыша»; б) разложив в ряд 4 случайно отобранные карточки, получим слово «план»?
6. Какова вероятность того, что трехзначный номер случайно взятого автомобиля: а) имеет все одинаковые цифры; б) имеет все различные цифры?
7. Найти вероятность того, что наугад взятое двухзначное число окажется: а) кратным 2; б) кратным 5; в) кратным 2-м и 5-ти одновременно.
8. Из цифр 1,2,3,4,5,6,7 составляются трехзначные числа при условии. Что ни одна цифра не повторяется. Какова вероятность того, что: а) это будет число 765; б) трехзначное число будет состоять из цифр 7,6,5?
9. В урне находится 5 шаров, их которых 3 красных. Найти вероятность того, что из трех взятых шаров два будут красными, если: а) выбор происходит без возврата; б) после каждого выбора шар возвращается в урну.
10. На полку ставят четырехтомник Лермонтова. Какова вероятность того, что: а) все тома будут расставлены по порядку; б) на своем месте будет только первый том?
11. Три спортсмена участвуют в соревнованиях. Вероятность зачисления в сборную команду первого, второго и третьего соответственно равны 0,8; 0,7; 0,6. Найти вероятность того, того, что: а) только один спортсмен попадает в сборную; б) хотя бы один попадает в сборную.
12. Вероятность своевременного прибытие каждого поезда дальнего следование равна 0,9. Какова вероятность того, что: а) 4 последовательно прибывших поезда прибудут без опоздания; б) хотел бы один поезд не опоздает?
13. Вероятности успешной сдачи экзамена по первому, второму и третьему предмету у данного студента равны 0,6; 0,7; 0,8. Найти вероятность того, что он: а) сдаст все экзамены; б) не сдаст хотя бы один экзамен; в) сдаст только первый экзамен.
14. Вероятность того, что человек в возрасте 60 лет не умрет в ближайший год, равна 0,9. Страховая компания страхует на год жизни двух людей 60-ти лет. Какова вероятность того, что компания: а) будет платить хотя бы по одному страховому полису; б) будет платить только по одному полису?
15. Студент пришёл на зачёт, зная из 30 вопросов только 24. Какова вероятность сдать зачёт, если после отказа отвечать на вопрос преподаватель задает один вопрос?
16. Брошены три монеты. Предлагая, что элементарные события равновероятны, найти вероятность событий: А = <монета выпала «гербом вверх»>, В = <выпало ровно два «герба»>, С = <выпало не более двух «гербов»>.
17. Сортировочная станция для приема имеет 3 пути. Вероятность того, что пути свободны, соответственно равны 0,2; 0,3; 0,4. Определить вероятность того, что: а)хотя бы один путь свободен; б)все пути свободны; в)только один путь занят.
18. Вероятность наличие свободного места в самолете 0,8; на поезде-0,7; на теплоходе-0,6. Определить вероятность: а) наличие хотя бы одного свободного места; б) наличие свободных мест только на одном виде транспорта; в) наличие свободных мест только на поезде.
19. Турист приехал в город, в котором две гостиницы. Вероятность наличие свободных мест в первой гостинице-0,8, во второй-0,6. Определить вероятность наличия свободных мест хотя бы в одной из гостиниц.
20. Вероятность того, что частный предприниматель получит ссуду в первом, втором, третьем банке равна соответственно 0,4; 0,5; 0,6. Предприниматель последовательно обращается во все три банка, начиная с первого. В следующий банк предприниматель обращается лишь в случае отказа в предыдущем банке. Какова вероятность того, что он получит ссуду?
21. На склад поступает продукция трех фабрик, причем первая фабрика поставляет 20%, вторая 30%, третья 50% изделий. Первая фабрика производит 0,5% нестандартных деталей, вторая и третья – 0,3% и 0,2% соответственно. Со склада наудачу выбирают одно изделие, которое оказалось нестандартным. Найти вероятность того, что оно изготовлено на второй фабрике.
22. В сеансе одновременной игры в шахматы с гроссмейстером играют 10 перворазрядников и 15 второразрядников. Вероятность того, что в таком сеансе перворазрядник выиграет у гроссмейстера, равна 0,2; для второразрядника эта вероятность равна 0,1. Случайно выбранный участник выиграл. Какова вероятность, что это был второразрядник?
23. Турист решивший отдохнуть в США, узнал, что в июле в Калифорнии бывает в среднем 20 солнечных дней, во Флориде 22, а на Гавайях – 24. Из трех рассматриваемых проспектов он случайным образом выбирает один и отправляется в соответствующее место. Турист приехал на отдых и попал под дождь. Какова вероятность того, что он отдыхал на Гавайях?
24. Имеются три одинаковых по виду ящика. В первом ящике 7 белых и 8 черных шаров, во втором 10 белых, в третьем 5 черных шаров. Из выбранного наугад ящика вынули белый шар. Найти вероятность того, что он взят из второго ящика?
26. В первой урне 3 белых и 5 черных шара, во второй 7 белых и 2 черных шара. Из второй урны переложили в первую один шар, а затем из первой урны вынули шар, который оказался черным. Найти вероятность того, что он ранее находился в первой урне?
27. Из десяти студентов, пришедших сдавать экзамен по математике, Иванов знает 5 билетов из 30, Петров – 25, Сидоров – 20, А остальные по 15. Преподаватель случайным образом выбирает первого студента из этой группы студентов. Этот студент сдал экзамен. Какова вероятность что он – Петров?
28. В группе спортсменов 20 лыжников, 5 велосипедистов, 4 легкоатлета. Вероятность выполнить квалификационную норму равна: для лыжника 0,7; для велосипедиста 0,8; для легкоатлета 0,9. Первый спортсмен выполнил норму. Какова вероятность, что он велосипедист?
29. Из продаваемого в магазине молока 40% поставляет первый молокозавод, второй – 60%. В среднем 9 из 1000 пакетов первого поставщика не выдерживают транспортировки, и разгерметизируется, а у второго – 1 из 250. Случайно выбранный пакет оказался разгерметизированным. Найти вероятность того, что он произведен на первом заводе?
30. Дальтониками являются 5% мужчин и 0,25% женщин. Наудачу выбранное лицо оказалось дальтоником. Какова вероятность того, что это был мужчина?
31 – 40.Вероятность того, что в локомотивном депо расход электроэнергии превысит суточную норму, равна р.
1)Какова вероятность того, что за n рабочих дней будет зафиксирован перерасход электроэнергии в течение m дней? Произвести вычисление: а) по формуле Бернулли; б) по формуле Пуассона; в) по локальной теореме Лапласа. Сделать вывод.
2) Найти вероятность того, что перерасхода энергии не будет хотя бы в течение (n-2) дней, используя: а) формулу Бернулли; б) интегральную теорему Лапласа.
42. В урне имеются 4 шара с номерами от 1 до 4. Случайным образом вынимают 2 шара. Случайная величина 

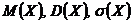
43. Вероятность выигрыша на один лотерейный билет равна р = 0,3. Случайная величина 

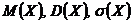
44. На некоторой остановке автобус останавливается только по требованию. Вероятность остановки равна 0,3. За смену автобус проходит мимо этой остановки 4 раза. Составить закон распределения случайной величины 

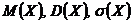
45. Из урны, содержащей 2 белых и 3 черных шара, извлекается 3 шара. Случайная величина 

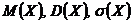
46. Трижды подбрасывается монета. Случайная величина 
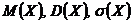
47. Два представителя одной команды участвуют в соревнованиях. Один из них попадает в финал за 1 – 3 места, причем вероятность занять первое место 0,2; второе – 0,3. Второй участник команды попадает в утешительный финал за 4 – 6 места, где его вероятность быть четвертым и пятым одинакова, и равна 0,4. Составить закон распределения случайной величины 

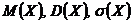
48. Вероятность рождения мальчика р = 0,5. Составить закон распределения случайной величины 

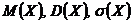
49. Подбрасывание колец на колышек производится до первого попадания либо до полного израсходования всех трех имеющихся колец. Вероятность попадания 0,7. Случайная величина 

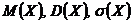
50. Трижды подбрасывается монета. Случайная величина 
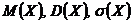
51 – 55. Задана непрерывная случайная величина X своей функцией распределения
1)найти плотность распределения 
2)определить коэффициент A;
3)схематично построить график функций 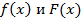
4)вычислить математическое ожидание и дисперсию;
5)определить вероятность того, что X примет значение из интервала 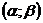
56 – 60. Задана непрерывная случайная величина X своей плотностью распределения вероятностей ƒ(x). Требуется:
1) определить коэффициент A;
2) найти функцию распределения F(x);
3) схематично построить график функций ƒ(x) и F(x);
4) вычислить математическое ожидание и дисперсию;
5) определить вероятность того, что X примет значение из интервала 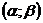
61 – 70. Нормально распределенная случайная величина Х задано своими параметрами а (математическое ожидание) и 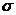
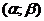
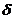
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
Математическая статистика
Дана двумерная выборка дискретных случайных величин 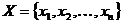
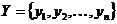
1. Построить вариационные ряды для величин 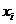
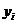
2. Используя вариационные ряды, составить интегральные ряды распределения величин 

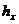
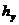
3. Построить гистограммы относительных интервальных частот величин 



4. Найти моду и медиану для интервальных распределений 

5. Используя данные вариационных рядов, найдите статистические средние значения, дисперсии и средние квадратические отклонения 



6. Найти доверительные интервалы для оценок математического ожидания и дисперсии величин 

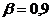
7. Считая средние интервальные значения 





8. В случае качественного совпадения графиков эмпирических и теоретических функций плотностей вероятностей проверить гипотезу о нормальном распределении случайных величин 

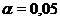
9. Используя интервальные ряды распределения, составить корреляционную таблицу.
10. Найти выборочный коэффициент корреляции в предположении линейной зависимости между 

11. Найти выборочные уравнения прямой линии регрессии 



| X | Y | X | Y | X | Y | X | Y | X | Y |
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.