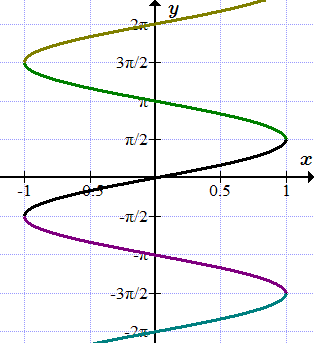Что называется функцией приведите примеры

Что такое Функция?

7 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие функции

Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.

1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.

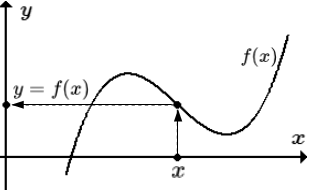
Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.

Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.

2. Функция — это определенное действие над переменной.

Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.

В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:

В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.

3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.

Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида

область определения выглядит так:

И записать это можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.

Источник

Что такое функция

Понятие функции – одно из основных в математике.

На уроках математики вы часто слышите это слово. Вы строите графики функций, занимаетесь исследованием функции, находите наибольшее или наименьшее значение функции. Но для понимания всех этих действий давайте определим, что такое функция.

Определение функции можно дать несколькими способами. Все они будут дополнять друг друга.

1. Функция – это зависимость одной переменной величины от другой. Другими словами, взаимосвязь между величинами.

Чем больше глубина, тем больше давление жидкости. Можно сказать, что давление жидкости является функцией от глубины, на которой его измеряют.

2. Можно дать и другое определение.

Функция – это определенное действие над переменной.

Итак, функция – это действие над переменной. В этом значении слово «функция» применяется и в областях, далеких от математики. Например, можно говорить о функциях мобильного телефона, о функциях головного мозга или функциях депутата. Во всех этих случаях речь идет именно о совершаемых действиях.

3. Дадим еще одно определение функции – то, что чаще всего встречается в учебниках.

Функция – это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.

Но зачем здесь такое длинное уточнение: «каждому элементу первого множества соответствует один и только один элемент второго»? Оказывается, что соответствия между множествами тоже бывают разные.

Могут быть и другие типы соответствий между множествами. Возьмем для примера компанию друзей и месяцы, в которые они родились:

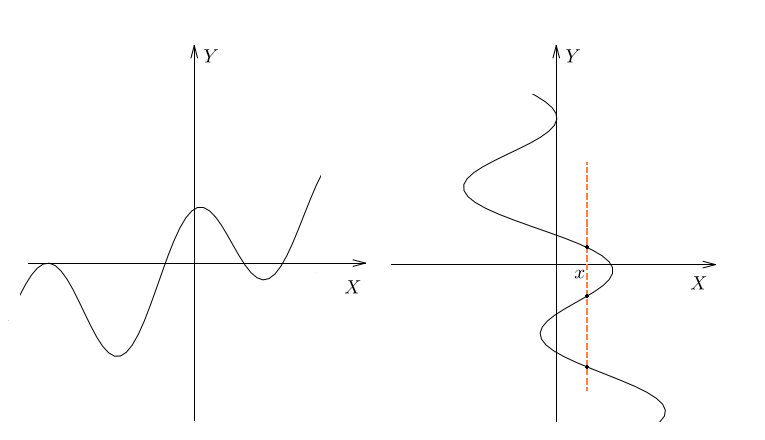
Каждый человек родился в какой-то определенный месяц. Но данное соответствие не является взаимно-однозначным. Например, в июне родились Сергей и Олег.

А каким должно быть соответствие между двумя множествами, чтобы оно не являлось функцией? Очень просто! Возьмем ту же компанию друзей и их хобби:

Мы видим, что в первом множестве есть элементы, которым соответствует два или три элемента из второго множества.

Очень сложно было бы описать такое соответствие математически, не правда ли?

Вот другой пример. На рисунках изображены кривые. Как вы думаете, какая из них является графиком функции, а какая – нет?

Ты нашел то, что искал? Поделись с друзьями!

Перечислим способы задания функции.

Это примеры функций, заданных формулами.

К тому же не всегда легко вывести точную формулу функции. Например, курс доллара (то есть зависимость стоимости доллара от времени) можно показать только на графике.

Источник

Функции

Если две переменные величины находятся между собой в такой зависимости, что каждому значению одной переменной соответствует строго определённое значение другой, то первая величина называется аргументом, а вторая его функцией.

Функция — это зависимая переменная величина. Аргумент — это независимая переменная. Зависимость функции от аргумента называется функциональной зависимостью.

Если нужно указать на тот факт, что y функция от x, не акцентируя внимания на то, в какой именно зависимости находится функция от аргумента, то пишут просто:

Иногда, чтобы показать, что y зависит от x, пишут просто:

Обратите внимание, что вместо y и x могут использоваться любые другие буквы.

Значение y, соответствующее заданному значению x, называют значением функции. Все значения, которые принимает аргумент, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют множество значений функции. Для функции f приняты следующие обозначения:

D(f) — область определения функции
(множество значений аргумента).

E(f) — множество значений функции.

Пример. Возьмём формулу нахождения расстояния по скорости и времени:

где S — это расстояние, v — скорость, а t — время. Если взять скорость, равную 50 км/ч, то каждому неотрицательному значению t будет соответствовать строго определённое значение S:

Источник

Определение функции

Определение функции

Сложные функции

Действительные функции

В математическом анализе большую роль играют числовые функции.

Числовая функция – это функция, значениями которой являются действительные или комплексные числа.
Действительная или вещественная функция – это функция, значениями которой являются действительные числа.

Максимум и минимум

Действительные числа имеют операцию сравнения. Поэтому множество значений действительной функции может быть ограниченным и иметь наибольшее и наименьшее значения.

Верхняя и нижняя грани

Монотонные функции

Многозначные функции

Как следует из определения функции, каждому элементу x из области определения, ставится в соответствие только один элемент из множества значений. Но существуют такие отображения, в которых элемент x имеет несколько или бесконечное число образов.

Многозначная функция – это совокупность функций, определенных на некотором множестве.
Ветвь многозначной функции – это одна из функций, входящих в многозначную функцию.
Однозначная функция – это функция.

Сужение и продолжение функции

Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник

Основные элементарные функции: их свойства и графики

Основные элементарные функции, присущие им свойства и соответствующие графики – одни из азов математических знаний, схожих по степени важности с таблицей умножения. Элементарные функции являются базой, опорой для изучения всех теоретических вопросов.

Статья ниже дает ключевой материал по теме основных элементарных функций. Мы введем термины, дадим им определения; подробно изучим каждый вид элементарных функций, разберем их свойства.

Выделяют следующие виды основных элементарных функций:

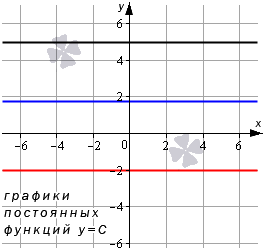
Постоянная функция

Свойства постоянных функций:

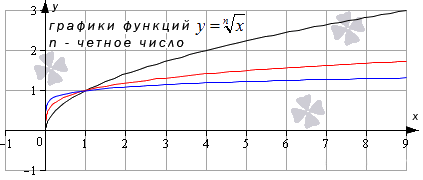
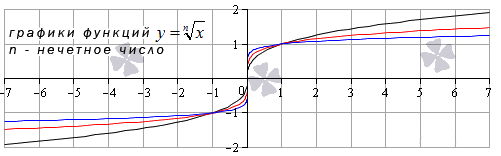
Корень n-й степени

Данная элементарная функция определяется формулой y = x n ( n – натуральное число больше единицы).

Рассмотрим две вариации функции.

Похожий вид у графиков функции четной степени при иных значениях показателя.

Свойства функции корень n-ой степени, n – четное число

Иные нечетные значения показателя корня функции y = x n дадут график аналогичного вида.

Свойства функции корень n-ой степени, n – нечетное число

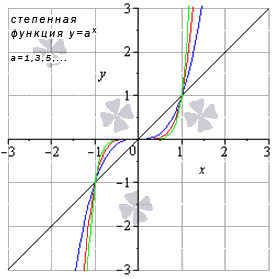
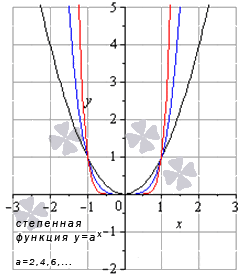
Степенная функция

Вид графиков и свойства функции зависят от значения показателя степени.

Степенная функция при нечетном положительном показателе

Свойства степенной функции, когда показатель степени – нечетный положительный

Степенная функция при четном положительном показателе

Свойства степенной функции, когда показатель степени – четный положительный:

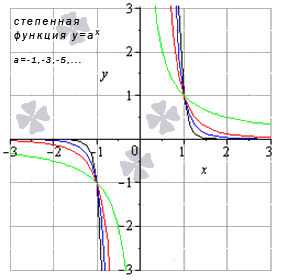
Степенная функция при нечетном отрицательном показателе

Свойства степенной функции, когда показатель степени – нечетный отрицательный:

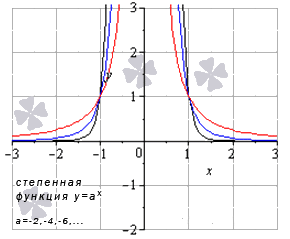
Степенная функция при четном отрицательном показателе степени

Свойства степенной функции, когда показатель степени – четный отрицательный:

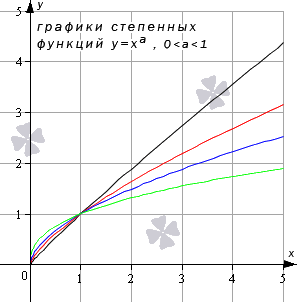
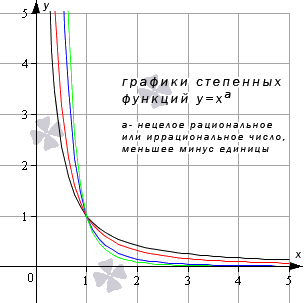
Степенная функция при рациональном или иррациональном показателе (значение больше нуля и меньше единицы)

Иные значения показателя степени a (при условии 0 a 1 ) дадут аналогичный вид графика.

Свойства степенной функции при 0 a 1 :

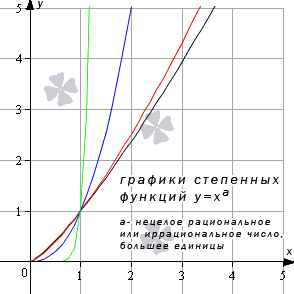
Степенная функция при нецелом рациональном или иррациональном показателе степени (больше единицы)

Иные значения показателя степени а при условии a > 1 дадут похожий вид графика.

Свойства степенной функции при a > 1 :

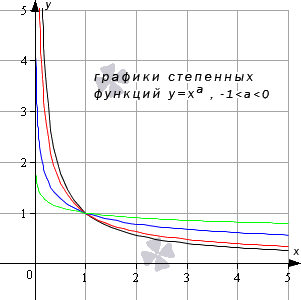
Степенная функция при действительном показателе степени (больше минус единицы и меньше нуля)

Степенная функция при нецелом действительном показателе степени (меньше минус единицы)

Показательная функция

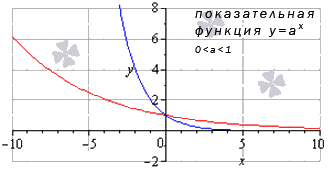
Сначала разберем ситуацию, когда основание показательной функции имеет значение от нуля до единицы ( 0 a 1 ) . Наглядным примером послужат графики функций при a = 1 2 (синий цвет кривой) и a = 5 6 (красный цвет кривой).

Свойства показательной функции, когда основание меньше единицы:

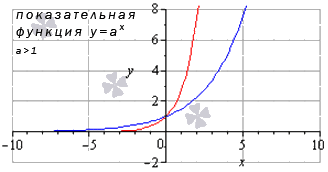
Проиллюстрируем этот частный случай графиком показательных функций y = 3 2 x (синий цвет кривой) и y = e x (красный цвет графика).

Иные значения основания, большие единицы, дадут аналогичный вид графика показательной функции.

Свойства показательной функции, когда основание больше единицы:

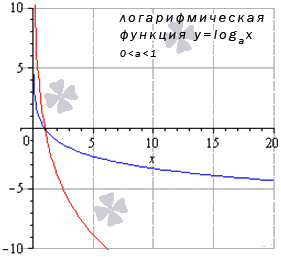
Логарифмическая функция

График логарифмической функции имеет различный вид, исходя из значения основания а.

Иные значения основания, не большие единицы, дадут аналогичный вид графика.

Свойства логарифмической функции, когда основание меньше единицы:

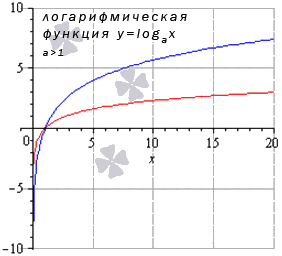
Теперь разберем частный случай, когда основание логарифмической функции больше единицы: а > 1 . На чертеже ниже – графики логарифмических функций y = log 3 2 x и y = ln x (синий и красный цвета графиков соответственно).

Иные значения основания больше единицы дадут аналогичный вид графика.

Свойства логарифмической функции, когда основание больше единицы:

Тригонометрические функции, их свойства и графики

Тригонометрические функции – это синус, косинус, тангенс и котангенс. Разберем свойства каждой из них и соответствующие графики.

В общем для всех тригонометрических функций характерно свойство периодичности, т.е. когда значения функций повторяются при разных значениях аргумента, отличающихся друг от друга на величину периода f ( x + T ) = f ( x ) ( T – период). Таким образом, в списке свойств тригонометрических функций добавляется пункт «наименьший положительный период». Помимо этого, будем указывать такие значения аргумента, при которых соответствующая функция обращается в нуль.

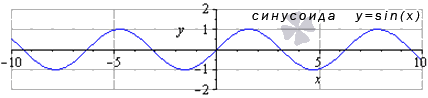
График данной функции называется синусоида.

Свойства функции синус:

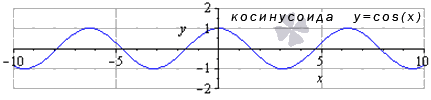
График данной функции называется косинусоида.

Свойства функции косинус:

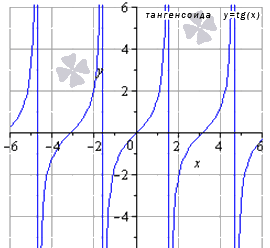
График данной функции называется тангенсоида.

Свойства функции тангенс:

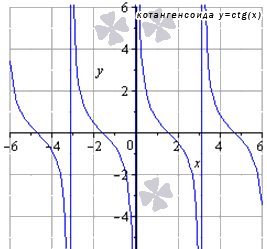
График данной функции называется котангенсоида.

Свойства функции котангенс:

Обратные тригонометрические функции, их свойства и графики

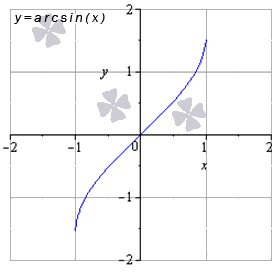
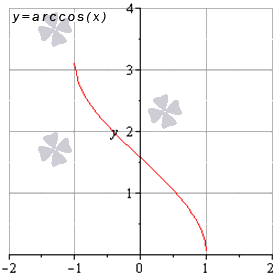
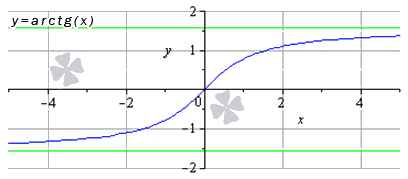
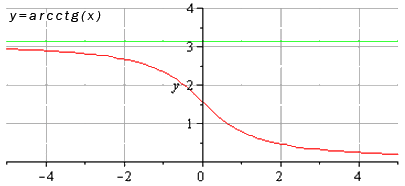
Обратные тригонометрические функции – это арксинус, арккосинус, арктангенс и арккотангенс. Зачастую, в связи с наличием приставки «арк» в названии, обратные тригонометрические функции называют аркфункциями.

Свойства функции арксинус:

Свойства функции арккосинус:

Свойства функции арктангенс:

Свойства функции арккотангенс:

Источник