Что называется функцией отклика

Что называется функцией отклика

Функция отклика

К задачам поиска оптимальных условий проведения эксперимента можно отнести выбор оптимального состава многокомпонентных смесей или сплавов, определение направлений повышения качества продукции, производительности оборудования и т. д. Для решения поставленной задачи объект исследования представляется в виде кибернетической системы. Изучение ее выполняется с помощью математической модели, представляющей уравнение связи (функцию отклика) параметра оптимизации с факторами, воздействующими на объект. Каждый фактор имеет несколько уровней значений. Фиксированный набор уровней факторов определяет одно из возможных состояний объекта. Если перебрать все возможные состояния, то получится полное множество состояний объекта, т. е. число возможных опытов. Но такое число оказывается очень большим и равняется числу р уровней факторов, возведенных в степень, равную числу факторов /с, т. е. pk. Задача планирования эксперимента и сводится к тому, чтобы сократить количество опытов до разумного минимума. [c.49]

Можно построить и более сложные конструкции, описывающие форму взаимодействия Центра и производственных единиц. Было, однако, показано, что все более сложные ситуации сводятся к ситуациям 1, 2 и 3, причем наиболее выгодной Центру оказывается вторая ситуация, далее следуют третья и первая. Задачи поиска наилучших механизмов стимулирования (в первом случае надо найти конечное число величин, во втором — функции, в третьем — функционалы, заданные на всех возможных функциях отклика производственных единиц), как удалось показать, можно свести к некоторым специальным задачам математического программирования. [c.356]

Установлено, что в пределах изменения безразмерных факторов эксперимента, максимальное значение коэффициента замещения обеспечивается при наименьших отношениях пластической и вязкостной составляющих буровых и тампонажных растворов, максимальных скоростях потока, а также при условиях наименьшей разницы в плотностях замещающей и замещаемой жидкостей. Безразмерное уравнение регрессии рекомендовано использовать в качестве функции отклика при оптимизации процесса замещения. [c.244]

В регрессионном анализе рассматриваются односторонняя зависимость случайной переменной Y от одной (или нескольких) неслучайной независимой переменной X. Такая зависимость может возникнуть, например, в случае, когда при каждом фиксированном значении X соответствующие значения Y подвержены случайному разбросу за счет действия ряда неконтролируемых факторов. Такая зависимость Гот X (иногда ее называют регрессионной) может быть также представлена в виде модельного уравнения регрессии 7 по X (3.1). При этом зависимую переменную У называют также функцией отклика, объясняемой, выходной, результирующей, эндогенной переменной, результативным признаком, а независимую переменную X — объясняющей, входной, [c.51]

В качестве функции отклика можно использовать различные критерии эффективности, в том числе коэффициент технической готовности парка машин J u. Установлено, что прослеживается закономерность [c.253]

Мы пересмотрели свою теорию с целью введения для каждого района сбыта трех функций отклика. Это означало, что суммарные функции отклика могли существенно отличаться друг от друга для разных районов вследствие различий в соотношении числа жителей, потребляющих пиво в больших, в умеренных и в малых количествах. [c.179]

Процесс моделирования связан с рядом процедур, например, таких как выбор целевой функции (функции отклика), переменных, параметров и т.д. Рассмотрим основные из них. [c.16]

Для проверки линейности уравнения регрессии используется следующий подход. Так как изменение функции отклика вносит случайный характер, то при каждом значении рекомендуется проводить по несколько экспериментов, чтобы для данного значения А получить некоторое среднее значение Y. [c.90]

В практике часто возникают ситуации, когда функция отклика (цели) Y зависит не от одного, а от многих факторов. Установление формы связи в этих случаях начинают, как правило, с рассмотрения линейной регрессии вида [c.109]

С помощью матрицы Rk, вычисляют частные коэффициенты корреляции, показывающие степень влияния одного из факторов х. на функцию отклика Упри условии, что остальные факторы имеют постоянные значения. [c.116]

Если необходимо изучить степень тесноты связи между функцией отклика У и несколькими факторами xl,x2. xp, (р

Смотреть страницы где упоминается термин Функция отклика

Источник

Что называется функцией отклика

Для исследования зависимости реакции экологической системы от тех или иных факторов в современной науке используют метод функций отклика. Этот метод широко применяется в инженерных науках, например, теории автоматического регулирования или теории планирования эксперимента. Его суть заключается в использовании информации об отклике системы на известные воздействия для получения оператора перехода по схеме: воздействие реакция. В терминах теории сложных систем, динамика сложной открытой системы, каковой является экосистема, характеризуется описанием связи между входными и выходными сигналами.

Идея функций отклика восходит к работам немецкого агрохимика Митчерлиха, сформулированная в начале века как «закон физиологических взамосвязей» (1909, 1925). Митчерних утверждал, что величина урожая зависит от уровней всех фактров роста и тем самым противопоставлял свой закон принципу минимума Либиха.

В современной экологической литературе (Одум, 1975, 1986; Федоров, Гельманов, 1980; Левич и др., 1997) закон толерантности рассматривается как продолжение и расширение принципа Либиха. Лимитирующим при этом называют фактор, по которому для достижения заданного относительного изменения функции отклика необходимо минимальное относительное изменение значения фактора. Такое определение требует подробного изучения зависимости функций отклика от всей совокупности экологических факторов в каждом конкретном случае, что связано с использованием приемов многофакторного эксперимента и аппарата многомерной математической статистики. Практическое использование такого подхода к исследованию большинства природных экосистем затруднено из-за недостатка экспериментальных данных и отсутствия систематических наблюдений.

Применение метода функций отклика для описания сложных экологических систем подразумевает решение задачи идентификации нелинейных систем достаточно большой размерности и стало возможным лишь в последние десятилетия 20 века в связи с появлением принципиально новых возможностей обработки временных рядов, новых пакетов решения систем дифференциальных уравнений, новых оптимизационных пакетов для проведения процедуры идентификации параметров, новых информационных технологий. Важным вопросом моделирования систем на основе метода функций отклика является анализ и обработка экспериментальных данных и использование робастных процедур, приводящих к тому, что результаты обработки мало зависят от наличия данных с большими ошибками

Наиболее часто используемые на практике частные функции отклика:

Формирование обобщенной функции отклика представляет собой наиболее сложную задачу. Обычно используют мультипликативное представление, позволяющее очертить в многомерном пространстве факторов границу толерантности системы:

Задача идентификации обобщенной функции отклика является задачей нелинейной регрессии с достаточно большим количеством параметров идентификации. Задача не может быть упрощена путем снижения ее размерности за счет выделения отдельных частных функций отклика или путем линейной аппроксимации, так как эти процедуры неправомерны в силу сложности системы и неоднозначности связей ее компонентов.

В отличие от классических моделей популяционной динамики и гидродинамики параметры функции отклика не имеют физического или биологического смысла, однако их сочетания, определяющие положение кардинальных точек (например, максимумов) частных функций отклика, могут иметь конкретный биологический смысл и называются параметрами связи. Они также используются при решении задачи идентификации. При решении задачи идентификации параметров в качестве начальных приближений можно использовать экспериментальные данные по отдельным процессам (частным функциям отклика).

Аппарат функций отклика успешно применялись для решения проблем, связанных с анализом отклика лесных экосистем на изменения окружающей среды (Teller, 1992), изучения проблем риска (Hubert, 1996). Разработка теории функций отклика и их применение для широкого круга задач экологической экспертизы и формирования индексов качества окружающей среды представлены в работах И.Г.Малкиной-Пых и Ю.А.Пых (1991,1997, 1998). В этих работах также решаются практические задачи прогнозирования продуктивности сортов сельскохозяйственных культур, оптимизации режимов орошения и внесения удобрений, прогнозирования последствий загрязнения территории радионуклидами, предсказания самоочищения звеньев экосистемы системы от различных поступивших загрязнителей, в том числе пестицидов, прогнозирования динамики органического вещества почв при их использовании для производства сельскохозяйственной продукции и др.

Источник

Функция отклика

19. Функция отклика

Зависимость математического ожидания отклика от факторов

Смотреть что такое «Функция отклика» в других словарях:

функция отклика — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN response function … Справочник технического переводчика

Оценочная функция отклика — 66. Оценочная функция отклика Функция отклика, в которой неизвестные значения параметров заменены их оценками Источник: РДМУ 109 77: Методические указания. Методика выбора и оптимизации контролируемых … Словарь-справочник терминов нормативно-технической документации

функция — 2.1 функция (function): Реализация в программе алгоритма, по которому пользователь или программа могут частично или полностью выполнять решаемую задачу. Примечания 1 Пользователю нет необходимости вызывать функцию (например, автоматическое… … Словарь-справочник терминов нормативно-технической документации

функция калибровки — 3.6 функция калибровки: Функция, связывающая математическое ожидание отклика с приведенной переменной состояния X. Примечания1) 1 При изображении функции калибровки на графике отклик обычно откладывают по ординате, а приведенную переменную… … Словарь-справочник терминов нормативно-технической документации

РЕАКЦИИ ФУНКЦИЯ — (отклика функция) в статистической физике ф ция, представляющая реакцию статистич. системы на зависящее от времени внеш. возмущение. Если на систему действуют зависящие от времени внеш. силы (напр., электрич. или магн. поля), то вызываемое ими… … Физическая энциклопедия

критическое значение отклика — 3.9 критическое значение отклика: Значение отклика Y, превышение которого для заданной вероятности ошибки a приводит к решению о том, что наблюдаемая система не находится в базовом состоянии. Примечания 1 Если приведенная переменная состояния… … Словарь-справочник терминов нормативно-технической документации

ПЕРЕДАТОЧНАЯ ФУНКЦИЯ — линейной стационарной системы управления (системы автоматич. регулирования) Лапласа преобразование отклика системы на воздействие единичной импульсной функции (дельта функции) 6 (г) при нулевых условиях в момент t=0 (сам этот отклик наз. функцией … Математическая энциклопедия

спектр действия (реакции, ответа, отклика) однокомпонентной акселерограммы — 3.30 спектр действия (реакции, ответа, отклика) однокомпонентной акселерограммы: Функция, связывающая между собой максимальное по модулю ускорение одномассового линейного осциллятора и соответствующий этому ускорению период (либо частоту)… … Словарь-справочник терминов нормативно-технической документации

спектр отклика однокомпонентной акселерограммы — 3.49 спектр отклика однокомпонентной акселерограммы : Функция, связывающая между собой максимальное по модулю ускорение одномассового линейного осциллятора и соответствующий этому ускорению период (либо частоту) собственных колебаний того же… … Словарь-справочник терминов нормативно-технической документации

Источник

Что такое отклик? Функция отклика. Поверхность отклика.

Что такое отклик? Функция отклика. Поверхность отклика.

Классификация видов экспериментальных исследований

5. Назовите методы планирования эксперимента, применяемые на разных этапах исследования.

Что такое ошибка опыта? Классификация ошибок опыта.

Ошибки параллельных опытов

Каждый эксперимент содержит элемент неопределен­ности вследствие ограниченности экспериментального ма­териала. Постановка повторных (или параллельных) опытов не дает полностью совпадающих результатов, потому что всегда существует ошибка опыта (ошибка воспроиз­водимости). Эту ошибку и нужно оценить по параллель­ным опытам. Для этого опыт воспроизводится по возмож­ности в одинаковых условиях несколько раз и затем бе­рется среднее арифметическое всех результатов. Среднее арифметическое равно сумме всех п отдельных резуль­татов, деленной на количество параллельных опытов п

.

Отклонение результата любого опыта от среднего арифметического можно представить как разность где – результат отдельного опыта. Наличие откло­нения свидетельствует об изменчивости, вариации значе­ний повторных опытов. Для измерения этой изменчи­вости чаще всего используют дисперсию. Диспер­сией называется среднее значение квадрата отклонений величины от ее среднего значения. Дисперсия обозна­чается s 2 и выражается формулой

.

где (n – 1) – число степеней свободы, равное количе­ству опытов минус единица. Одна степень свободы исполь­зована для вычисления среднего.

Корень квадратный из дисперсии, взятый с положи­тельным знаком, называется средним квадратическим от­клонением, стандартом или квадратичной ошибкой

Стандарт имеет размерность той величины, для кото­рой он вычислен. Дисперсия и стандарт – это меры рассеяния, изменчивости. Чем больше дисперсия и стан­дарт, тем больше рассеяны значения параллельных опы­тов около среднего значения.

Ошибка опыта являемся суммарной величиной, результатом многих ошибок: ошибок измерений факторов, ошибок измерений параметра оптимизации и др. Каждую из этих ошибок можно, в свою очередь, разделить на состав­ляющие.

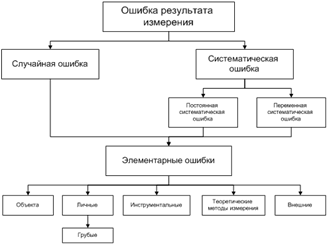
Вопрос о классификации ошибок довольно сложный и вызывает много дискуссий. В качестве примера одной из возможных схем классификации мы приведем схему из книги Ю. В. Кельница «Теория ошибок измере­ний» (М., изд-во «Недра», 1967).

Все ошибки принято разделять на два класса: система­тические и случайные.

Систематические ошибки порождаются причинами, действующими регулярно, в определенном направлении. Чаще всего эти ошибки можно изучить и определить количественно.

Систематические ошибки находят, калибруя измери­тельные приборы и сопоставляя опытные данные с изме­няющимися внешними условиями (например, при градуи­ровке термопары по реперным точкам, при сравнении с эта­лонным прибором).

Если систематические ошибки вызываются внешними условиями (переменной температуры, сырья и т. д.), следу­ет компенсировать их влияние. Как это делать, будет показано ниже.

Случайными ошибками называются те, которые появ­ляются нерегулярно, причины возникновения которых неизвестны и которые невозможно учесть заранее.

Систематические и случайные ошибки состоят из мно­жества элементарных ошибок. Для того, чтобы исключать инструментальные ошибки, следует проверять приборы перед опытом, иногда в течение опыта и обязательно после опыта. Ошибки при проведении самого опыта возникают вследствие неравномерного нагрева реакционной среды, раз­ного способа перемешивания и т.п. При повторении опытов такие ошибки могут вызвать большой разброс эксперимен­тальных результатов.

Очень важно исключить из экспе­риментальных данных грубые ошибки, так называемый брак при повторных опытах. Для отброса оши­бочных опытов существуют правила. Для определения брака используют, например, кри­терий Стьюдента

.

Значение t берут из таблицы t-распределения Стьюдента. Опыт считается бракованным, если эксперименталь­ное значение критерия t по модулю больше табличного значения.

Что такое фактор? Классификация факторов. Требования, предъявляемые к факторам.

Определение фактора

Фактором называется измеряемая переменная ве­личина, принимающая в некоторый момент времени определенное значение. Факторы соответствуют способам воз­действия на объект исследования.

Также, как и параметр оптимизации, каждый фактор имеет область определения. Мы будем считать фактор заданным, если вместе с его названием указана область его определения. Под областью определения понимается совокупность всех значений, которые в принципе может принимать данный фактор, Ясно, что совокупность зна­чений фактора, которая используется в эксперименте, является подмножеством из множества значений, обра­зующих область определении.

Область определения может быть непрерывной и дис­кретной. Однако в тех задачах планирования экспери­мента, которые мы собираемся рассматривать, всегда ис­пользуются дискретные области определения. Так, для факторов с непрерывной областью определения, таких, как температура, время, количество вещества и т. п., всегда выбираются дискретные множества уровней.

В практических задачах области определения факторов, как правило, ограничены. Ограничения могут носить принципиальный либо технический характер.

Произведем классификацию факторов и зависимости от того, является ли фактор переменной величиной, кото­рую можно оценивать количественно: измерять, взвеши­вать, титровать и т.п., или же он – некоторая перемен­ная, характеризующаяся качественными свойствами.

Факторы разделяются на коли­чественные и качественные. Качественные факторы – это разные вещества, разные технологические способы, ап­параты, исполнители и т. д.

Хотя качественным факторам не соответствует число­вая шкала в том смысле, как это понимается для коли­чественных факторов, однако можно построить условную порядковую шкалу, которая ставит в соответствие уров­ням качественного фактора числа натурального ряда, т. е. производит кодирование. Порядок уровней может быть произволен, но после кодирования он фиксируется.

В ряде случаев граница между понятием качественного и количественного фактора весьма условна. Пусть, на­пример, при изучении воспроизводимости результатов хи­мического анализа надо установить влияние положения тигля с навеской в муфельной печи. Можно разделить под печи на квадраты и считать номера квадратов уровнями качественного фактора, определяющего положение тигля. Вместо этого можно ввести два количественных фактора – ширину и длину пода печи. Качественным фак­торам не соответствует числовая шкала, и порядок уров­ней факторов не играет роли.

Требования, предъявляемые к факторам при планировании эксперимента

При планировании эксперимента факторы должны быть управляемыми. Это значит, что экспери­ментатор, выбрав нужное значение фактора, может его поддерживать постоянным в течение всего опыта, т. е. может управлять фактором. В этом состоит особенность «активного» эксперимента. Планировать эксперимент мож­но только в том случае, если уровни факторов подчиняются воле экспериментатора.

Чтобы точно определить фактор, нужно указать последовательность действий (операций), с помощью ко­торых устанавливаются его конкретные значения (уровни). Такое определение фактора будем называть опера­циональным. Так, если фактором является давление в некотором аппарате, то совершенно необходимо указать, в какой точке и с помощью какого прибора оно измеряется и как оно устанавливается. Введение операционального определения обеспечивает однозначное понимание фак­тора.

Точность замера факторов должна быть возможно более высокой. Степень точности определяется диапазоном изменения факторов. При изучении процесса, который длится десятки часов, нет необходимости учиты­вать доли минуты, а в быстрых процессах необходимо учитывать, быть может, доли секунды.

Факторы должны быть непосредственными воздейст­виями на объект. Факторы должны быть однозначны. Трудно управлять фактором, который является функцией других факторов. Но в планировании могут участвовать сложные факторы, такие, как соотношения между компонентами, их логарифмы и т. п.

Необходимость введения сложных факторов возникает при желании представить динамические особенности объекта в статической форме. Пусть, например, тре­буется найти оптимальный режим подъема температуры в реакторе. Если относительно температуры известно, что она должна нарастать линейно, то в качестве фактора вместо функции (в данном случае линейной) можно ис­пользовать тангенс угла наклона, т. е. градиент. Положе­ние усложняется, когда исходная температура не зафик­сирована. Тогда ее приходится вводить в качестве еще одного фактора. Для более сложных кривых пришлось бы ввести большее число факторов (производные высоких порядков, координаты особых точек и т. д.). Поэтому целесообразно пользоваться сложным качественным фак­тором – номером кривой. Различные варианты кривых рассматриваются в качестве уровней. Это могут быть разные режимы термообработки сплавов, переходные процессы в системах управления и т. д.

Требования к совокупности факторов

При планировании эксперимента обычно одно­временно изменяется несколько факторов. Поэтому очень важно сформулировать требования, которые предъяв­ляются к совокупности факторов. Прежде всего, выдви­гается требование совместимости. Совместимость факторов означает, что все их комбинации осуществимы и безопасны. Это очень важное требование. Представьте себе, что вы поступили легкомысленно, не обратили внима­ния на требование совместимости факторов и запланиро­вали такие условия опыта, которые могут привести к взрыву установки или осмолению продукта. Согласитесь, что такой результат очень далек от целей оптимиза­ции.

Несовместимость факторов может наблюдаться на гра­ницах областей их определения. Избавиться от нее можно сокращением областей. Положение усложняется, если несовместимость проявляется внутри областей определе­ния. Одно из возможных решений – разбиение на под­области и решение двух отдельных задач.

При планировании эксперимента важна независи­мость факторов, т. е. возможность установления факто­ра на любом уровне вне зависимости от уровней других факторов. Если это условно невыполнимо, то невозможно планировать эксперимент. Итак, мы подошли ко второму требованию – отсутствию корреляции между факторами. Требование некоррелированности не означает, что между значениями факторов нет никакой связи. Достаточно, что­бы связь не была линейной.

Множественная регрессия

Виды НИР в промышленности

Методическая программа НИР

Что такое отклик? Функция отклика. Поверхность отклика.

Источник