Что называется фигурами лиссажу
Фигуры Лиссажу
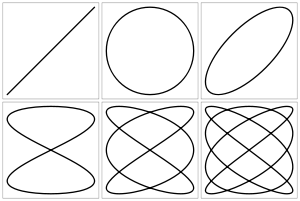
Фигу́ры Лиссажу́ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Жюлем Антуаном Лиссажу. Вид фигур зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или 
вырождаются в отрезки прямых, а при разности фаз 
и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний неточно совпадают, то разность фаз всё время меняется, вследствие чего эллипс всё время деформируется. При существенно различных периодах фигуры Лиссажу не наблюдаются. Однако, если периоды относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в то же положение — получаются фигуры Лиссажу более сложной формы. Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, равных амплитудам колебаний.
Математическое выражение для кривой Лиссажу
где A, B — амплитуды колебаний, a, b — частоты, δ — сдвиг фаз
Вид кривой сильно зависит от соотношения a/b. Когда соотношение равно 1, фигура Лиссажу имеет вид эллипса, при определённых условиях она имеет вид прямой (A = B, δ = π/2 радиан) и отрезка прямой (δ = 0). Ещё один пример фигуры Лиссажу — парабола (a/b = 2, δ = π/2). При других соотношениях фигуры Лиссажу представляют собой более сложные фигуры, которые являются замкнутыми при условии a/b — рациональное число.
являются полиномами Чебышева первого рода степени N.
Примеры
Анимация внизу показывает изменение кривых при постоянно возрастающем соотношении 
от 0 до 1 с шагом 0.01. (δ=0)
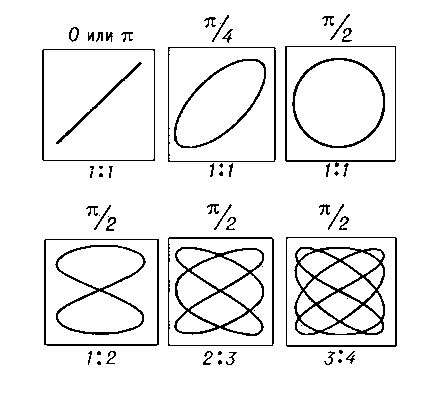
Примеры фигур Лиссажу ниже с δ = π/2, нечётным натуральным числом a, и также натуральным числом b, и |a − b| = 1.
Применение в технике — сравнение частот
Если подать на входы «X» и «Y» осциллографа сигналы близких частот, то на экране можно увидеть фигуры Лиссажу. Этот метод широко используется для сравнения частот двух источников сигналов и для подстройки одного источника под частоту другого. Когда частоты близки, но не равны друг другу, фигура на экране вращается, причем период цикла вращения является величиной, обратной разности частот, например, период оборота равен 2 с — разница в частотах сигналов равна 0,5 Гц. При равенстве частот фигура застывает неподвижно, в любой фазе, однако на практике, за счет кратковременных нестабильностей сигналов, фигура на экране осциллографа обычно чуть-чуть подрагивает. Использовать для сравнения можно не только одинаковые частоты, но и находящиеся в кратном отношении, например, если образцовый источник может выдавать частоту только 5 МГц, а настраиваемый источник — 2,5 МГц.
Литература
См. также
Ссылки
Полезное
Смотреть что такое «Фигуры Лиссажу» в других словарях:
фигуры Лиссажу — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN Lissajous figures … Справочник технического переводчика
Лиссажу фигуры — Фигуры Лиссажу замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Ж. Лиссажу (J. Lissajous; 1822 80). Вид фигур… … Википедия
Лиссажу, Жюль Антуан — Жюль Антуан Лиссажу (фр. Jules Antoine Lissajous; 4 марта 1822, Версаль, Франция … Википедия
Фигуры Хладни — Примеры фигур Хладни из книги Э.Хладни «Акустика» Фигуры Хладни фигуры, о … Википедия
ЛИССАЖУ ФИГУРЫ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонич. колебания в двух взаимно перпендикулярных направлениях. Впервые изучены франц. учёным Ж. Лиссажу (J. Lissajous). Вид Л. ф. зависит от соотношения между периодами… … Физическая энциклопедия
ЛИССАЖУ ФИГУРЫ — замкнутые траектории, описываемые точкой, совершающей одновременно два гармонических колебательных движения в двух взаимно перпендикулярных направлениях. Вид этих фигур зависит от соотношения между периодами (частотами), фазами и амплитудами… … Большая политехническая энциклопедия
ЛИССАЖУ ФИГУРЫ — [по имени франц. физика Ж. Лиссажу (J. Lissajous; 1822 80)] замкнутые траектории точки, совершающей одновременно 2 гармонич. колебат. движения в двух взаимно перпендикулярных направлениях. Вид Л. ф. зависит от соотношений между периодами… … Большой энциклопедический политехнический словарь
ЛИССАЖУ ФИГУРЫ — замкнутые траектории точки, совершающей одновременно два гармонич. колебат. движения в двух взаимно перпендикулярных направлениях. Вид Л.ф. зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний и позволяет… … Естествознание. Энциклопедический словарь
Лиссажу фигуры — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Ж. Лиссажу (J. Lissajous; 1822 80). Вид Л. ф. зависит от… … Большая советская энциклопедия
Фигура Лиссажу — Фигуры Лиссажу замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Ж. Лиссажу (J. Lissajous; 1822 80). Вид фигур… … Википедия
Что называется фигурами лиссажу
Этот топик не приурочен ко дню рождения, но всё-таки пару слов скажу об авторе.
Жюль Антуан Лиссажу (фр. Jules Antoine Lissajous; 4 марта 1822, Версаль, Франция — 24 июня 1880) — французский математик, в честь которого названы фигуры Лиссажу. Член-корреспондент Парижской Академии наук (1879).
Родился в Версале 4 марта 1822 года. Учился в лицее Гоша́ (Версаль). Стал профессором в лицее Луи, в 1850 году представил диссертацию о вибрирующей решётке. Изучал акустические колебания. Умер в 1880 году.
А вообще просто хочу рассказать и показать «красивые картинки». Наверняка многие с ними знакомы, но всё равно, надеюсь, что это будет интересно!
Фигуры Лиссажу
Фигуры Лиссажу — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Жюлем Антуаном Лиссажу. Вид фигур зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или `pi` вырождаются в отрезки прямых, а при разности фаз `pi/2` и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний неточно совпадают, то разность фаз всё время меняется, вследствие чего эллипс всё время деформируется. При существенно различных периодах фигуры Лиссажу не наблюдаются. Однако, если периоды относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в то же положение — получаются фигуры Лиссажу более сложной формы. Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, равных амплитудам колебаний.
где A, B — амплитуды колебаний, a, b — частоты, δ — сдвиг фаз
Вид кривой сильно зависит от соотношения a/b. Когда соотношение равно 1, фигура Лиссажу имеет вид эллипса, при определённых условиях она имеет вид окружности (A = B, δ = π/2 радиан) и отрезка прямой (δ = 0). Ещё один пример фигуры Лиссажу — парабола (a/b = 2, δ = π/2). При других соотношениях фигуры Лиссажу представляют собой более сложные фигуры, которые являются замкнутыми при условии a/b — рациональное число.
Фигуры Лиссажу, где a = 1, b = N (N — натуральное число) и
`delta=(N-1)/N * pi/2`
являются полиномами Чебышёва первого рода степени N.
Примеры
Много красивого Анимация внизу показывает изменение кривых при постоянно возрастающем соотношении a/b от 0 до 1 с шагом 0.01. (δ=0)
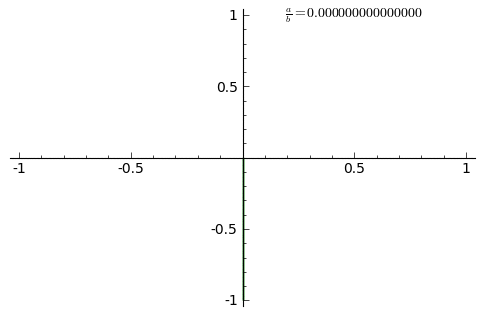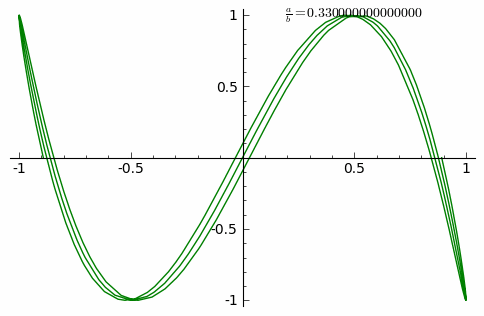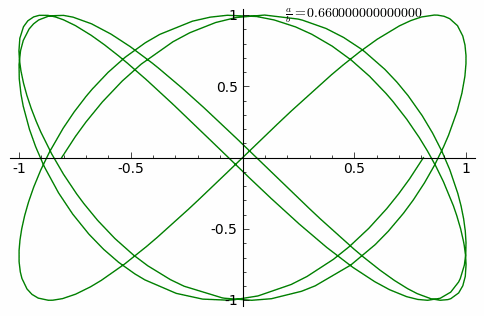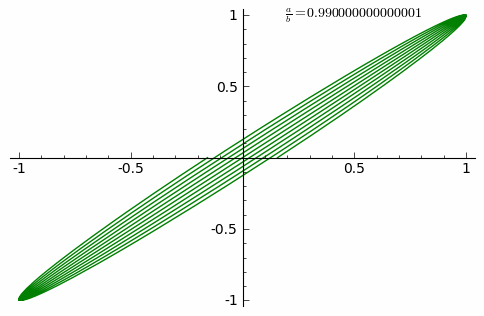
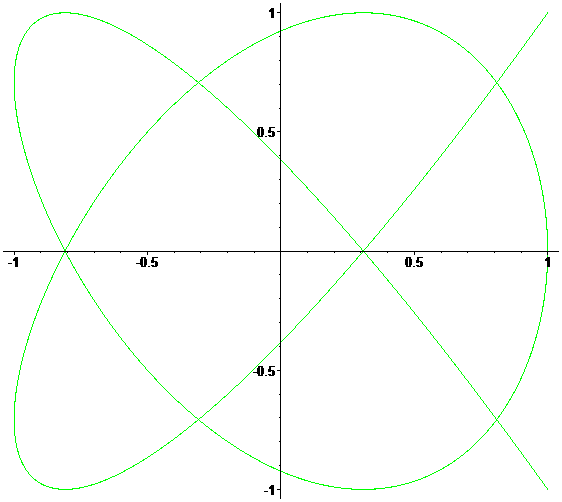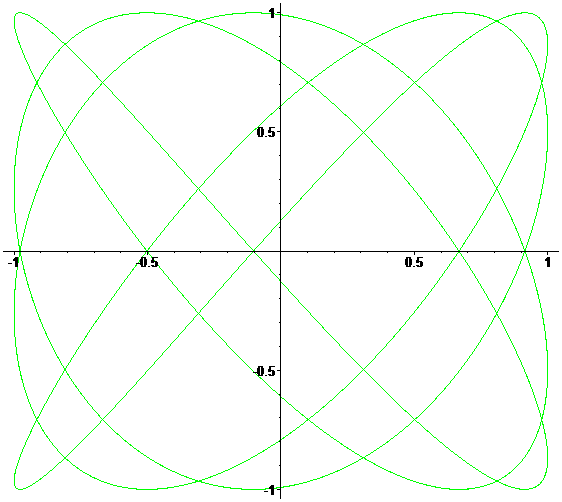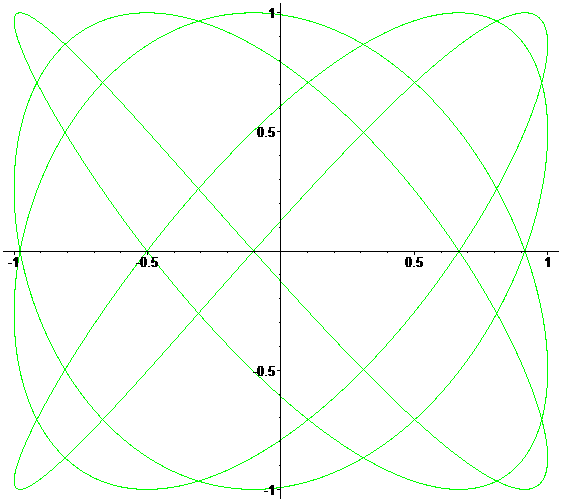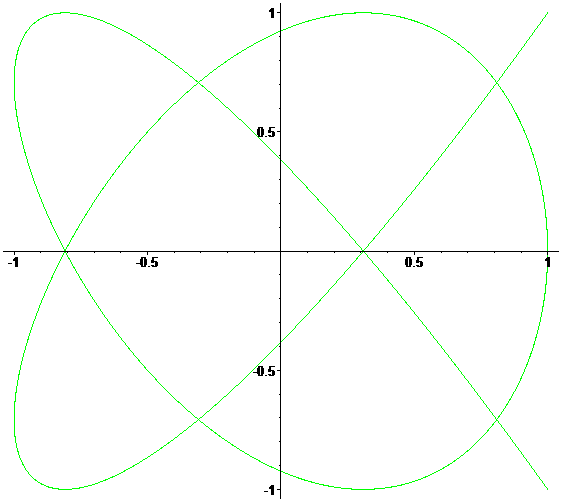
Два видео от НИЯУ МИФИ: фигуры Лиссажу из песка и на экране осциллографа. Очень впечатляет!
читать дальше
И вот напоследок, для тех, кто посмотрел на фигуры Лиссажу на осциллографе, а также, для тех, кто скептически воспринимает нынешние реалии, демотиватор.
Фигуры Лиссажу
Что такое фигуры Лиссажу?
Фигуры Лиссажу представляют из себя различные геометрически-красивые рисунки, которые вычерчиваются точкой, колеблющейся в двух взаимно-перпендикулярных направлениях на одной плоскости.
Чтобы было более понятно, давайте представим девочку на качели из покрышки:
И вот представьте, что сзади ее раскачивает папа, а сбоку — мама. То есть наша девочка будет одновременно летать вперед-назад, а также влево-вправо. Долго ли она продержится — это уже другой вопрос). Если в солнечный денек посмотреть на землю, то мы увидим, что тень девочки вырисовывает различную траекторию полета.
Почему бы нам не поиграться пучком электронов, отклоняя его одновременно и по вертикали и по горизонтали? Вспоминаем, как выглядит электронно-лучевая трубка осциллографа:
1 — это горизонтальные пластины
2 — вертикальные пластины
ну и остальные детали — это составляющие электронной пушки.
Подаем на вертикальные пластины один синусоидальный сигнал, а на горизонтальные — другой синусоидальный сигнал. В результате точка на осциллографе будет вырисовывать различные линии и кривые, в зависимости от частоты сигналов. Хотя, цифровой осциллограф и аналоговый почти не похожи по внутренней начинке, но принцип действия у них все равно схож.
Как получить фигуры Лиссажу
Итак, для того, чтобы вырисовывать фигуры Лиссажу, нам потребуются два генератора частоты.
и осциллограф с функцией XY-режима. В моем случае это цифровой осциллограф OWON
Думаю, почти во всех современных осциллографах есть режим XY, будь это аналоговый или цифровой осциллограф.
Режим XY-осциллографа
Как вы помните, при простом использовании осциллографа у нас по оси X было время, а по оси Y — напряжение. Поэтому, по умолчанию, мы на осциллографе смотрим изменение напряжения во времени. Но если с помощью нехитрой кнопки переключить в режим XY, то у нас по Y будет напряжение и по X…. тоже напряжение, но уже с другого генератора частоты. Если включить в таком режиме только один генератор, то мы увидим только одну прямую линию либо по вертикали, либо по горизонтали. Это аналогично тому, если бы нашу девочку раскачивал только папа или только мама. Наша девочка летела бы только по одной прямой траектории.
А что будет, если сбоку нашу девочку будет раскачивать мама, а сзади — папа? Тут уже траектория девочки будет хаотичной. Но во всяком хаосе рождается порядок. И первым его заметил французский математик Жюль Антуан Лиссажу.
Строим фигуры Лиссажу на осциллографе
Цепляем на один канал один генератор частоты, а на другой канал — другой генератор частоты:
На осциллографе мы должны увидеть два сигнала с разных генераторов частоты, благо у меня осциллограф двухканальный:
Теперь переводим осциллограф в режим XY. На моем осциллографе это делается с помощью кнопки Display
Ну а потом с помощью дисплейных клавиш выбираем режим XY
И получается примерно вот такая хаотическая картинка:
Ну еще бы, один генератор дергает точку по X, другой по Y и у каждого генератора разная частота.
А давайте возьмем один генератор и с него подадим сигнал на два канала сразу. Частота и фаза совпадают и на первом и втором канале, так как мы берем сигнал с одного и то же генератора. В результате у нас будет вот такая картинка:
Если взять 100 Герц на первом генераторе и на втором генераторе, то получим что-то типа этого:
В реальности же получается круг, который все время крутится и превращается то в эллипс, то в прямую, так как очень ровно подобрать частоту на первом и втором генераторе очень сложно. Хотя на практике можно подавать сигнал на один канал напрямую, а на другой — через фазовращатель.
Если увеличить частоту на одном из генераторов вдвое, то можно наблюдать уже другие фигуры:
Эта фигура тоже все время крутится на осциллографе.
Увеличиваем на одном генераторе частоту в кратное число раз, то есть было 100, потом 200, 300 и тд и получаем абсолютно новые 3D фигуры 😉
Различное отношение частот одного генератора к другому дает различные фигуры Лиссажу:
Вот такие фигуры вы будете видеть на экране своего осциллографа:
А вот такие фигуры Лиссажу получаются, если использовать пилообразный сигнал с обоих генераторов сразу при разных отношениях коэффициентов
А вот такие фигуры получаются, если на одном оставить синус, а на втором поставить пилу:
Лиссажу фигуры
Смотреть что такое «Лиссажу фигуры» в других словарях:
Лиссажу фигуры — Фигуры Лиссажу замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Ж. Лиссажу (J. Lissajous; 1822 80). Вид фигур… … Википедия
ЛИССАЖУ ФИГУРЫ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонич. колебания в двух взаимно перпендикулярных направлениях. Впервые изучены франц. учёным Ж. Лиссажу (J. Lissajous). Вид Л. ф. зависит от соотношения между периодами… … Физическая энциклопедия
ЛИССАЖУ ФИГУРЫ — замкнутые траектории, описываемые точкой, совершающей одновременно два гармонических колебательных движения в двух взаимно перпендикулярных направлениях. Вид этих фигур зависит от соотношения между периодами (частотами), фазами и амплитудами… … Большая политехническая энциклопедия
ЛИССАЖУ ФИГУРЫ — [по имени франц. физика Ж. Лиссажу (J. Lissajous; 1822 80)] замкнутые траектории точки, совершающей одновременно 2 гармонич. колебат. движения в двух взаимно перпендикулярных направлениях. Вид Л. ф. зависит от соотношений между периодами… … Большой энциклопедический политехнический словарь
ЛИССАЖУ ФИГУРЫ — замкнутые траектории точки, совершающей одновременно два гармонич. колебат. движения в двух взаимно перпендикулярных направлениях. Вид Л.ф. зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний и позволяет… … Естествознание. Энциклопедический словарь
Фигуры Лиссажу — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Жюлем Антуаном Лиссажу. Вид фигур зависит от соотношения между… … Википедия
фигуры Лиссажу — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN Lissajous figures … Справочник технического переводчика
Лиссажу, Жюль Антуан — Жюль Антуан Лиссажу (фр. Jules Antoine Lissajous; 4 марта 1822, Версаль, Франция … Википедия
Фигуры Хладни — Примеры фигур Хладни из книги Э.Хладни «Акустика» Фигуры Хладни фигуры, о … Википедия
Фигура Лиссажу — Фигуры Лиссажу замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Ж. Лиссажу (J. Lissajous; 1822 80). Вид фигур… … Википедия
Физика Б1.Б8.
Электронное учебное пособие по разделу курса физики Механика
Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.
Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.
Введение
Механика – это раздел физики, который изучает наиболее простой вид движения материи – механическое движение и причины, вызывающие или изменяющие это движение.
Механическое движение – это изменение во времени взаимного расположения тел или частей одного и того же тела. Причиной, вызывающей механическое движение тела или его изменение, является воздействие со стороны других тел.
Развитие механики началось еще в древние времена, однако, как наука она формировалась в средние века. Основные законы механики установлены итальянским физиком и астрономом Г. Галилеем (1564-1642) и английским ученым И. Ньютоном (1643-1727).
Механику Галилея-Ньютона принято называть классической механикой. В ней изучается движение макроскопических тел, скорости которых значительно меньше скорости света с в вакууме. Законы движения тел со скоростями, близкими к скорости света сформулированы А. Эйнштейном (1879-1955), они отличаются от законов классической механики. Теория Эйнштейна называется специальной теорией относительности и лежит в основе релятивистской механики. Законы классической механики неприемлемы к описанию движения микроскопических тел (элементарных частиц – электронов, протонов, нейтронов, атомных ядер, самих атомов и т.д.) их движение описывается законами квантовой механики.
Механика состоит из трех разделов: кинематики, динамики и статики. Кинематика дает математическое описание движения, не касаясь причин, которыми вызвано движение. Динамика – основной раздел механики, она изучает законы движения тел и причины, которыми вывзывается движение и его изменение. Статика изучает законы равновесия системы тел под действием приложенных сил. Мы ограничимся изучением двух основных разделов – кинематики и динамики.
В механике для описания движения в зависимости от условий решаемой задачи пользуются различными упрощающими моделями: материальная точка, абсолютно твердое тело, абсолютно упругое тело, абсолютно неупругое тело, и т.д. Выбор той или иной модели диктуется необходимостью учесть в задаче все существенные особенности реального движения и отбросить несущественные, усложняющие решение.
Материальная точка – это тело обладающее массой, размеры и форма которого несущественны в данной задаче. Любое твердое тело или систему тел можно рассматривать как систему материальных точек. Для этого любое тело или тела системы нужно мысленно разбить на большое число частей так, чтобы размеры каждой части были пренебрежимо малы по сравнению с размерами самих тел.
Абсолютно твердое тело – это тело, расстояние между любыми точками которого остается неизменным в процессе движения или взаимодействия. Эта модель пригодна, когда можно пренебречь деформацией тел в процессе движения.
Абсолютно упругое и абсолютно неупругое тело – это два предельных случая реальных тел, деформациями которых можно и нельзя пренебречь в изучаемых процессах.
Любое движение рассматривается в пространстве и времени. В пространстве определяется местоположение тела, во времени происходит смена местоположений или состояний тела в пространстве, время выражает длительность состояния движения или процесса. Пространство и время –это два фундаментальных понятия, без которых теряется смысл понятия движения: движения не может быть вне времени и пространства.