Что называется элементарной ячейкой кристаллической решетки

Кристаллическая решётка. Элементарная ячейка

Структура кристалла– это конкретное расположение частиц в пространстве (физическая реальность). Чтобы представить структуру кристалла, нужно знать относительные размеры частиц, расстояния между ними, силы связи ме­жду частицами, их взаимное расположение, повторяющее расположение частиц в пространстве (пространственную решётку), и законы симметрических преоб­разований.

Симметрия– основная особенность, характерная для структуры кристаллов. Теорию строения структуры кристаллов развил английский учёный Бравэ, основываясь на многих экспериментальных результатах других исследовате­лей. Положив в основу своей теории анизотропию и симметрию кристаллов, он пришёл к понятию о пространственной решётке.

Рис. 1.11.Пространственные решётки некоторых веществ

Рассмотрим простейший случай, когда одинаковые частицы расположены в кристалле параллельными бесконечными рядами. На 1 мм в кристалле находится порядка 10 7 частиц (рис. 1.12). Трансляция(период идентичности) –симметричное преобразование, при котором точка (частица) повторяется в пространстве. Её величина – кратчайшее из возможных расстояний между одина­ковыми точками в ряду.

Рис. 1.12.Линейная цепочка атомов

Если сдвинуть точки бесконечного ряда на один период идентичности вдоль направления трансляции, то ряд совместится сам с собой, его вид не на­рушится. Выбор основных трансляций в структуре кристалла очень важен, по­тому что ими определяются кристаллографические системы координат. В об­щем случае это косоугольные координаты с разными масштабными отрезками по осям (рис. 1.13).

Узлы ряда– одинаковые точки, связанные между собой величиной трансляции ав бесконечном ряду. При перенесении точек по трём направлениям на величину трансляций а, b, c можнополучить трёхмерную сетку.

Ячейки сетки– параллелограммы, вершины которых являются узлами.

Элементарная ячейка– параллелепипед с характерным для данной решётки расположением частиц, с помощью которого весь кристалл может быть построен путём его многократного повторения в трёх направлениях. Она стро­ится на трёх элементарных трансляциях а, b, с. Элементарную ячейку принято выбирать так, чтобы она удовлетворяла следующим условиям: наилучшим об­разом отражала симметрию сетки, имела бы прямые углы и, если возможно, обладала бы наименьшим объёмом.

Примитивнойназывается элементарная ячейка, внутри которой нет узлов, частицы содержатся только в вершинах (рис. 1.13). Узлы решётки– вершины ячеек, в которых располагаются одинаковые атомы или группы атомов. Они эк­вивалентны друг другу.

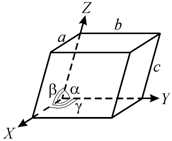
Период (постоянная) кристаллической ячейки– расстояние между однородными атомами. Параметры элементарной ячейки: три ребра ячейки a, b, c; три угла между ними α, β, γ. Например, для представленной на рис. 1.13 примитивной ячейки, соотношения между параметрами следующие:

Рис. 1.13.Примитивная элементарная ячейка

Элементарные ячейки, составляющие кристаллическую решётку кристалла, имеют одинаковые форму и объём. Кристалл можно построить с помощью разных примитивных ячеек. В некоторых случаях удобно характеризовать про­странственную сетку не примитивной, а сложной элементарной ячейкой, у ко­торой узлы есть не только в вершинах, но и внутри ячейки. Элементарная ячей­ка может содержать несколько примитивных ячеек.

Элементарные ячейкиразличаются по элементам симметрии и степени заполнения атомами (рис. 1.14).

Рис. 1.14.Разные примитивные ячейки в плоской сетке

К элементам симметрииотносятся: трансляции, плоскости симметрии, зеркальные плоскости, оси симметрии разных порядков, инверсионные оси симметрии (рис. 1.15).

Рис. 1.15. Элементы симметрии в кубическом кристалле

Кристаллические ячейки делятся по элементам симмет­рии на 7 сингоний:триклинная, моноклинная, ромбическая, ромбоэдрическая, гексагональная, тетрагональная, кубическая. Сингония в дословном переводе – сходноугольность. В сингонию объединяют кристаллы, у которых одинакова симметрия элементарных ячеек и одинаковая система координат.На рис. 1.16 показана тетрагональная ячейка.

Рис. 1.16. Кристаллическая ячейка тетрагональной сингонии

В каждой сингонии элементарные ячейки делятся по степени заполнения их атомами. Так на одну ячейку простой кубической ячейки имеет приходится 1 атом: n = (1/8)8 = 1; объёмноцентрированной кубической ячейки (ОЦК) – 2 атома: n = (1/8)8 + 1 = 2; гранецентрированной кубической ячейки (ГЦК) – 4 атома: n =(1/8)8 + (1/2)6 = 4 Рис. 1.17); гексагональной с плотной упаковкой (ГПУ) – 2 атома.

Рис. 1.17. Кристаллические ячейки

Кристаллическую решетку общего типа называют решеткой с базисом(БЦК). Решетка с базисом представляется в виде двух вставленных одна в другую подрешеток Бравэ, каждая из которых определяется трансляцион­ными векторами. Базисный вектор устанавливает смещение реше­ток друг относительно друга. Количество базисных векторов может быть сколь угодно большим.

Рис. 1.18.Решётки Браве

Все известные в природе кристаллические тела кристаллизуются в 14 ре­шётках Браве(рис. 1.18). Далее они делятся на 32 класса симметрии и 230 пространственных групп.

Некоторым телам свойственна не одна, а две или более кристаллических структур, устойчивых при различных температурах и давлениях. Такое явление называется полиморфизмом.Полиморфные формы (модификациивещества) имеют, например, углерод и олово. Углеродможет существовать в виде алмаза и графита. Алмаз очень прочный и твёрдый, графит – хрупкий. Элементарные ячейки алмаза и графита относятся к различным сингониям (рис. 1.19).

Рис. 1.19.Кристаллические решётки алмаза и графита

Оловоможет существовать в виде двух модификаций – серого и белого. Серое оловопри температурах ниже 13,3 °С. имеет решётку типа алмаза. При температурах выше 13,3 °С серое олово превращается в белое олово – очень хрупкое вещество, которое легко разрушается в порошок. Белое (металличе­ское) оловоимеет тетрагональную объёмноцентрированную решётку.

ИНДЕКСЫ МИЛЛЕРА

Для описания кристаллических многогранников и структур применяется метод индицирования.Через узлы кристаллической решетки можно провести прямые линии и плоскости. Выберем один из узлов решётки за начало координат.

Любой другой узел решётки определяется радиус–вектором:

Индексы узла– три простых числа [[mnp]], взятые в двойные квадратные или фигурные скобки (рис. 1.20). В системе параллельных прямых всегда можно выделить прямую линию (ряд), проходящую через начало координат. Тогда направление прямой линии определится двумя точками: началом координат и любым узлом ряда.

Индексы направления(прямой линии) – три простых числа [mnp], взятые в квадратные скобки. Эти числа характеризуют положение ближайшего узла, лежащего на прямой линии, проходящей через начало координат.

Рис. 1.20.Миллеровские индексы узлов

Проходящая сквозь узлы прямая, а также ребро кристаллического многогранника имеют наклон в выбранной системе координат. В целом плоские сет­ки в пространственной решётке и соответствующие им грани кристаллического многогранника имеют наклон в системе координат.

Пусть некоторая плоскость решётки пересекает все три оси координат, отсекая на них отрезки ma, nb, pc. Отношение чисел m:n:p характеризует наклон плоскости к осям координат. Серию отношений рациональных чисел m:n:p для всех параллельных плоско­стей можно заменить отношением взаимно простых чисел р:q:r. Числа р, q, r называются параметрами Вейса.

Миллеровские индексы плоскости– три простых числа (HKL), записанные в круглых скобках. Индексы плоскости – дополнительные множители к величинам, обратно пропорциональным числу осевых единиц, отсекаемых лю­бой плоскостью данного семейства на координатных осях Х, У, Z.

Миллеровские индексы опреде­ляются из соотношения чисел р:q:r.

Пусть некоторая плоскость отсекает на осях координат отрезки:

р =1, q = 3, c = 2 (рис. 1.21). Составим отношения:

Общий знаменатель равен 6. Дополнительные множители: H = 6, K = 2, L = 3.

Миллеровские индексы данной плоскости (623).

Рис.1.21. Индексы плоскости(623)

Межплоскостное расстояние– это расстояние между параллельными плоскостями, содержащими одинаковое количество атомов. Чем больше индексы H, K, L, тем меньше расстояние между плоскостями. Для кубического кристалла межплоскостное расстояние d для параллельных плоскостей с одинаковыми индексами выражаются через индексы этих плоскостей соотношением:

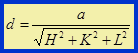
а– постоянная решётки.

В 1819 г. Гаюи сформулировал законцелых чисел(теперь закон Гаюи): для любых двух граней реального кристалла двойные отношения параметров равны отношению малых чисел. На кристаллографическом многограннике образуются лишь такие грани, для которых двойные отношения отрезков, отсекаемых данной гранью и еди­ничной гранью на трёх рёбрах кристалла, принятых за оси координат, равны отношению целых небольших простых чисел.

Грани, для которых отношение р:q:r является иррациональным, в реальном кристалле невозможны. Наклон всякой грани можно определить тремя целыми числами, если за оси координат выбрать направление трёх рёбер кристалла, а за параметры – отрезки, отсекае­мые на этих осях данной гранью.

Источник

Элементарная ячейка

Из Википедии — свободной энциклопедии

Элементарная ячейка — в геометрии, физике твёрдого тела и минералогии, в частности при обсуждении кристаллической решётки, минимальная ячейка, отвечающая единичной решёточной точке структуры с трансляционной симметрией в 2D, 3D или других размерностях.

Элементарная ячейка — фундаментальная область группы трансляций кристаллической решётки (решётки Браве).

Существует принципиальное различие между примитивной и элементарной ячейкой при рассмотрении структуры кристалла (англ. primitive unit cell, conventional unit cell ). Примитивной ячейкой называется минимальный воображаемый объём кристалла, параллельные переносы (трансляции) которого в трёх измерениях позволяют построить трёхмерную кристаллическую решётку в целом. Элементарной примитивная ячейка может называться только в том случае, когда она обладает теми же элементами симметрии, что и конечный объем. Таким образом при моделировании кристаллических структур оказывается удобнее использовать именно элементарную ячейку, так как она воспроизводит не только структуру, но в конечном счете и свойства кристалла.

Бравэ были сформулированы 3 правила выбора элементарных ячеек:

Содержимое элементарной ячейки позволяет охарактеризовать всю структуру минерала. Часть структуры, охватываемая элементарной ячейкой, состоит из атомов, удерживаемых вместе благодаря электронным связям. Такие мельчайшие ячейки, бесконечно повторяющиеся в трехмерном пространстве, образуют кристалл. Элементарная ячейка не является физическим телом, её можно передвигать по структуре параллельно самой себе, независимо от выбора начала координат ячейка будет содержать те же атомы в прежних количествах, так как структура периодична. Элементарная ячейка и представляет собой такой минимальный период в трёх измерениях.

Применяемые в кристаллографии элементарные ячейки имеют вид параллелепипедов, их форма и размер определяются заданием трёх некомпланарных трансляций (векторов) решётки, то есть трёх не лежащих в одной плоскости ребер ячейки. Ячейка полностью определяет решётку. Обратное неверно: в одной и той же решётке выбор ячейки может совершаться по-разному.

Ячейка, построенная на трёх кратчайших некомпланарных трансляциях решётки, называется основной ячейкой. Объём такой ячейки минимален, она содержит всего один узел кристаллической решётки, и относится поэтому к примитивным ячейкам. Нередко такая ячейка оказывается низкосимметричной, при том, что симметрия самой структуры выше. В таком случае выбирают другую, высокосимметричную ячейку большего объёма, с дополнительными узлами решётки (непримитивная, или центрированная ячейка).

При помощи рентгеноструктурного анализа определяют размеры элементарной ячейки минерала, его сингонию, вид симметрии и пространственную группу симметрии, а также расшифровывают кристаллическую структуру.

Источник

элементарная ячейка кристалла

Полезное

Смотреть что такое «элементарная ячейка кристалла» в других словарях:

ЭЛЕМЕНТАРНАЯ ЯЧЕЙКА КРИСТАЛЛА — часть кристаллической решетки, параллельные переносы которой в трех измерениях (трансляции) позволяют построить всю кристаллическую решетку. Выбор элементарной ячейки кристалла производится различными способами. Элементарная ячейка кристалла в… … Большой Энциклопедический словарь

элементарная ячейка кристалла — Смотри элементарная ячейка (элементарная ячейка кристалла) … Энциклопедический словарь по металлургии

ЭЛЕМЕНТАРНАЯ ЯЧЕЙКА КРИСТАЛЛА — часть кристаллич. решётки, параллельные переносы к рой в трёх измерениях (трансляции) позволяют построить всю кристаллич. решётку. Выбор Э.я. к. производится разл. способами. Э. я. к. в общем случае имеет форму параллелепипеда. Длины рёбер… … Естествознание. Энциклопедический словарь

элементарная ячейка (элементарная ячейка кристалла) — [unit cell] элементарная часть кристаллической решетки, параллельные переносы которой (трансляции) в трех измерениях позволяют построить всю кристаллическую решетку. Смотри также: Ячейка электролитическая ячейка гранецентрированная ячейка… … Энциклопедический словарь по металлургии

ЭЛЕМЕНТАРНАЯ ЯЧЕЙКА — кристалла, часть ат. структуры кристалла, параллельными переносами к рой (трансляциями) в трёх измерениях можно построить всю крист. решётку. Э. я. имеет форму параллелепипеда, выбор её определяется симметрией кристаллов. (см. КРИСТАЛЛИЧЕСКАЯ… … Физическая энциклопедия

элементарная ячейка — Смотри элементарная ячейка (элементарная ячейка кристалла) … Энциклопедический словарь по металлургии

Элементарная ячейка — Элементарная ячейка в геометрии, физике твёрдого тела и минералогии, в частности при обсуждении кристаллической решётки, минимальная ячейка, отвечающая единичной решёточной точке структуры с трансляционной симметрией в 2D, 3D или других… … Википедия

ЭЛЕМЕНТАРНАЯ ЯЧЕЙКА МАГНИТНАЯ — ЭЛЕМЕНТАРНАЯ ЯЧЕЙКА МАГНИТНАЯ, наименьшая совокупность групп атомов кристаллической решетки, периодическим повторением которой (трансляциями) получается вся магнитная структура кристалла. Кристаллическая элементарная ячейка может или совпадать с… … Энциклопедический словарь

Элементарная ячейка — кристалла, минимальный объём кристалла, параллельные переносы (трансляции) которого в трёх измерениях позволяют построить всю кристаллическую решётку. Выбор Э. я. может быть произведён различными способами … Большая советская энциклопедия

Ячейка — [cell]: Смотри также: электролитическая ячейка гранецентрированная ячейка базоцентрированная ячейка … Энциклопедический словарь по металлургии

Источник

Элементарная ячейка

Бравэ были сформулированы 3 правила выбора элементарных ячеек:

* Симметрия элементарной ячейки должна соответствовать симметрии кристалла.

* Элементарная ячейка должна иметь максимальное число равных ребер и равных углов.

* При условии выполнения двух первых правил элементарная ячейка должна иметь минимальный объем.

Содержимое элементарной ячейки позволяет охарактеризовать всю структуру минерала. Часть структуры, охватываемая элементарной ячейкой, состоит из атомов, удерживаемых вместе благодаря электронным связям. Такие мельчайшие ячейки, бесконечно повторяющиеся в трехмерном пространстве, образуют кристалл. Элементарная ячейка не является физическим телом, её можно передвигать по структуре параллельно самой себе, независимо от выбора начала координат ячейка будет содержать те же атомы в прежних количествах, так как структура периодична. Элементарная ячейка и представляет собой такой минимальный период в трёх измерениях.

Применяемые в кристаллографии элементарные ячейки имеют вид параллелепипедов, их форма и размер определяются заданием трёх некомпланарных трансляций (векторов) решётки, то есть трёх не лежащих в одной плоскости ребер ячейки. Ячейка полностью определяет решётку. Обратное неверно: в одной и той же решётке выбор ячейки может совершаться по-разному.

Ячейка, построенная на трёх кратчайших некомпланарных трансляциях решётки, называется основной ячейкой. Объём такой ячейки минимален, она содержит всего один узел кристаллической решётки, и относится поэтому к примитивным ячейкам. Нередко такая ячейка оказывается низкосимметричной, при том, что симметрия самой структуры выше. В таком случае выбирают другую, высокосимметричную ячейку большего объёма, с дополнительными узлами решётки (непримитивная, или центрированная ячейка).

При помощи рентгеноструктурного анализа определяют размеры элементарной ячейки минерала, его сингонию, вид симметрии и пространственную группу симметрии, а также расшифровывают кристаллическую структуру.

Связанные понятия

Кристаллографические группы, или фёдоровские группы — набор групп симметрий, которые описывают все возможные симметрии бесконечного количества периодически расположенных точек в трёхмерном пространстве.

Упоминания в литературе

Связанные понятия (продолжение)

Кристалл — вспомогательный геометрический образ, вводимый для анализа строения кристалла. Решётка имеет сходство с канвой или сеткой, что даёт основание называть точки решётки узлами. Решёткой является совокупность точек, которые возникают из отдельной произвольно выбранной точки кристалла под действием группы трансляции. Это расположение замечательно тем, что относительно каждой точки все остальные расположены совершенно одинаково. Применение к решётке в целом любой из присущих ей трансляций приводит.

Термин геометрическая координация используется в целом ряде смежных областей химии — химии/физики твердого тела и не только.

Три вектора (или большее число) называются компланарными, если они, будучи приведёнными к общему началу, лежат в одной плоскости.

Антиферромагнетик — вещество, в котором установился антиферромагнитный порядок магнитных моментов атомов или ионов. В антиферромагнетиках спиновые магнитные моменты электронов самопроизвольно ориентированы антипараллельно друг другу. Такая ориентация охватывает попарно соседние атомы. В результате антиферромагнетики обладают очень малой магнитной восприимчивостью и ведут себя как слабые парамагнетики.

Твёрдые растворы — фазы переменного состава, в которых атомы различных элементов расположены в общей кристаллической решётке.

Источник

Что называется элементарной ячейкой кристаллической решетки

Одним из основных представлений, связанных со структурой кристаллов, является понятие об элементарной ячейке. В общем случае элементарную ячейку можно представить, как минимальный объём кристалла, параллельные переносы (трансляции) которого в трёх измерениях позволяют построить всю кристаллическую решётку.

Закономерности строения элементарной ячейки, в частности степень их симметричности определяет многие свойства кристалла, в первую очередь электрические, магнитные и механические. Элементарная ячейка может содержать как один, так и несколько атомов. Так у многих металлов, например железа, хрома, меди, серебра, она состоит из одного атома. В тех случаях когда, кристалл состоит из нескольких химических элементов, например, натрия и хлора, элементарная ячейка будет содержать два атома: натрий и хлор. Широко распространены кристаллы с элементарной ячейкой, состоящей из нескольких сцепленных друг с другом молекулярных групп, например кристаллы льда или же многих магнитных материалов. Существуют кристаллы, например, белковые, элементарная ячейка которых состоит из молекул, содержащих несколько тысяч атомов.

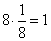
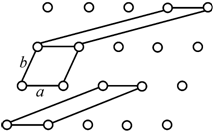
Каждый узел, находящийся в вершине элементарной ячейки, принадлежит еще восьми соседним элементарным ячейкам. Поскольку всего узлов (или вершин параллелепипеда) восемь, то ( ) и на примитивную элементарную ячейку приходится всего один узел.

Казалось бы, что выбор элементарной ячейки произволен. На рис. 1.6 все три плоские ячейки примитивны. Хотя трансляции в двух из них и не являются кратчайшими, но любая из них воспроизводит при переносе параллельно самой себе в двух направлениях всю «структуру кристалла». Однако Бравэ были сформулированы 3 правила выбора элементарных ячеек, выполняемые в указанной ниже последовательности.

1. Симметрия элементарной ячейки должна соответствовать симметрии кристалла.

2. Элементарная ячейка должна иметь максимальное число равных ребер и равных углов.

3. При условии выполнения двух первых правил элементарная ячейка должна иметь минимальный объем.

При выполнении этих правил элементарная ячейка, в отличие от примитивной, кроме узлов в вершинах, может иметь дополнительные узлы.

Рис. 1.5. Элементарная ячейка

Рис. 1.6. Различные способы выбора элементарных ячеек

Совокупность координат всех узлов, приходящихся на элементарную ячейку, часто называют ее базисом. Сложную ячейку обычно выбирают так, чтобы узлы находились либо в центрах граней, либо в центре объема. Поэтому принята система наиболее распространенных видов сложных ячеек.

Приведем примеры сложных элементарных ячеек в узлах которых находятся атомы одного сорта.

Источник