Что называется электроемкостью двух проводников
Учебники
Журнал «Квант»
Общие
Электроемкость
Электроемкость характеризует способность проводников или системы из нескольких проводников накапливать электрические заряды, а следовательно, и электроэнергию, которая в дальнейшем может быть использована, например, при фотосъемке (вспышка) и т.д.
Различают электроемкость уединенного проводника, системы проводников (в частности, конденсаторов).
Уединенным называется проводник, расположенный вдали от других заряженных и незаряженных тел так, что они не оказывают на этот проводник никакого влияния.
Электроемкость уединенного проводника — физическая величина, равная отношению электрического заряда уединенного проводника к его потенциалу\[
C = \frac<\varphi>\]. В СИ единицей электроемкости является фарад (Ф).
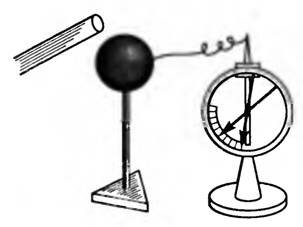
Электроемкость проводника не зависит от рода вещества и заряда, но зависит от его формы и размеров, а также от наличия вблизи других проводников или диэлектриков. Действительно, приблизим к заряженному шару, соединенному с электрометром, незаряженную палочку (рис. 1). Он покажет уменьшение потенциала шара. Заряд q шара не изменился, следовательно, увеличилась емкость. Это объясняется тем, что все проводники, расположенные вблизи заряженного проводника, электризуются через влияние в поле его заряда и более близкие к нему индуцированные заряды противоположного знака ослабляют поле заряда q.
Если уединенным проводником является заряженная сфера, то потенциал поля на ее поверхности \(
\varphi = \frac<4 \pi \varepsilon_0 \varepsilon R>\), где R — радиус сферы, ε — диэлектрическая проницаемость среды, в которой находится проводник. Тогда
электроемкость уединенного сферического проводника.
Взаимная электроемкость зависит от формы и размеров проводников, от их взаимного расположения и относительной диэлектрической проницаемости среды, заполняющей пространство между ними.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 236-237.
Учебники
Журнал «Квант»
Общие
Содержание
Электроемкость
Различают электроемкость уединенного проводника, системы проводников (в частности, конденсаторов).
Электроемкость уединенного проводника
В СИ единицей электроемкости является фарад (Ф).
Поскольку 1 Ф очень большая единица емкости, применяют дольные единицы:
Электроемкость проводника не зависит от рода вещества и заряда, но зависит от его формы и размеров, а также от наличия вблизи диэлектрика.
Если уединенным проводником является заряженная сфера, то потенциал поля на ее поверхности
где R — радиус сферы, ε — диэлектрическая проницаемость среды, в которой находится проводник. Тогда электроемкость уединенного сферического проводника
Электроемкость двух проводников
Обычно на практике имеют дело с двумя и более проводниками. Рассмотрим два проводника произвольной формы, находящиеся в однородном диэлектрике. Сообщим им заряды +q и –q. При этом между проводниками установится некоторая разность потенциалов (напряжение): φ1 – φ2 = U.
Эксперимент показывает, что увеличение заряда каждого проводника, например, в 2 раза приводит к увеличению напряжения между ними также в 2 раза, т.е. отношение \(\dfrac\) для данной пары проводника остается постоянным:
Электроемкость двух проводников зависит от формы и размеров проводников, от их взаимного расположения и относительной диэлектрической проницаемости среды, заполняющей пространство между ними.
Конденсаторы
Для практического использования электрической энергии необходимо уметь ее накапливать. Для этого используют специальные устройства — конденсаторы.
Проводники, из которых состоит конденсатор, называются обкладками.
Как правило, при зарядке конденсатора заряды его обкладок равны по величине и противоположны по знаку. Под зарядом конденсатора понимают значение заряда положительно заряженной обкладки.
При небольших размерах конденсатор отличается значительной емкостью, не зависящей от наличия вблизи него других зарядов или проводников.
Виды конденсаторов
Конденсаторы можно классифицировать по следующим признакам и свойствам:
Что называется электроемкостью двух проводников
При каком условии можно накопить на проводниках большой электрический заряд?
В сильном электрическом поле (при большом напряжении и соответственно при большой напряженности) диэлектрик (например, воздух) становится проводящим.
Возможен так называемый пробой диэлектрика: между проводниками проскакивает искра, и они разряжаются.
Чем меньше увеличивается напряжение между проводниками с увеличением их зарядов, тем больший заряд можно на них накопить.
Введем физическую величину, характеризующую способность двух проводников накапливать электрический заряд.
Эту величину называют электроемкостью.
Поэтому отношение заряда q одного из проводников (на другом находится такой же по модулю заряд) к разности потенциалов между этим проводником и соседним не зависит от заряда.
Оно определяется геометрическими размерами проводников, их формой и взаимным расположением, а также электрическими свойствами окружающей среды.
Это позволяет ввести понятие электроемкости двух проводников.
Электроемкостью двух проводников называют отношение заряда одного из проводников к разности потенциалов между ними:
Электроёмкость уединённого проводника равна отношению заряда проводника к его потенциалу, если все другие проводники бесконечно удалены и потенциал бесконечно удалённой точки равен нулю.
На проводниках можно накопить большие заряды, не вызывая пробоя диэлектрика.
Но сама электроемкость не зависит ни от сообщенных проводникам зарядов, ни от возникающего между ними напряжения.
Формула (14.22) позволяет ввести единицу электроемкости.
Эту единицу называют фарад (Ф); 1 Ф = 1 Кл/В.
Систему проводников очень большой электроемкости вы можете обнаружить в любом радиоприемнике или купить в магазине. Называется она конденсатором. Сейчас вы узнаете, как устроены подобные системы и от чего зависит их электроемкость.
Большой электроемкостью обладают системы из двух проводников, называемые конденсаторами. Конденсатор представляет собой два проводника, разделенные слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Проводники в этом случае называются обкладками конденсатора.
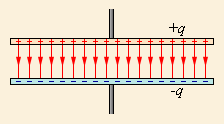
Простейший плоский конденсатор состоит из двух одинаковых параллельных пластин, находящихся на малом расстоянии друг от друга (рис.14.33).
Если заряды пластин одинаковы по модулю и противоположны по знаку, то силовые линии электрического поля начинаются на положительно заряженной обкладке конденсатора и оканчиваются на отрицательно заряженной (рис.14.28). Поэтому почти все электрическое поле сосредоточено внутри конденсатора и однородно.
Для зарядки конденсатора нужно присоединить его обкладки к полюсам источника напряжения, например к полюсам батареи аккумуляторов. Можно также первую обкладку соединить с полюсом батареи, у которой другой полюс заземлен, а вторую обкладку конденсатора заземлить. Тогда на заземленной обкладке останется заряд, противоположный по знаку и равный по модулю заряду незаземленной обкладки. Такой же по модулю заряд уйдет в землю.
Под зарядом конденсатора понимают абсолютное значение заряда одной из обкладок.
Электроемкость конденсатора определяется формулой (14.22).
Электрические поля окружающих тел почти не проникают внутрь конденсатора и не влияют на разность потенциалов между его обкладками. Поэтому электроемкость конденсатора практически не зависит от наличия вблизи него каких-либо других тел.
Электроемкость плоского конденсатора.
Геометрия плоского конденсатора полностью определяется площадью S его пластин и расстоянием d между ними. От этих величин и должна зависеть емкость плоского конденсатора.
Чем больше площадь пластин, тем больший заряд можно на них накопить: q
S. С другой стороны, напряжение между пластинами согласно формуле (14.21) пропорционально расстоянию d между ними. Поэтому емкость
Кроме того, емкость конденсатора зависит от свойств диэлектрика между пластинами. Так как диэлектрик ослабляет поле, то электроемкость при наличии диэлектрика увеличивается.
Проверим на опыте зависимости, полученные нами из рассуждений. Для этого возьмем конденсатор, у которого расстояние между пластинами можно изменять, и электрометр с заземленным корпусом (рис.14.34). Соединим корпус и стержень электрометра с пластинами конденсатора проводниками и зарядим конденсатор. Для этого нужно коснуться наэлектризованной палочкой пластины конденсатора, соединенной со стержнем. Электрометр покажет разность потенциалов между пластинами.
Раздвигая пластины, мы обнаружим увеличение разности потенциалов. Согласно определению электроемкости (см. формулу (14.22)) это указывает на ее уменьшение. В соответствии с зависимостью (14.23) электроемкость действительно должна уменьшаться с увеличением расстояния между пластинами.
Кроме того, ёмкость конденсатора зависит от свойств диэлектрика между пластинами. Так как диэлектрик ослабляет поле, то электроёмкость при наличии диэлектрика увеличивается: 
где ε — диэлектрическая проницаемость диэлектрика.
Последовательное и параллельное соединения конденсаторов. На практике конденсаторы часто соединяют различными способами. На рисунке 14.40 представлено последовательное соединение трёх конденсаторов.
Определить эквивалентную электроёмкость — это значит определить электроёмкость такого конденсатора, который при той же разности потенциалов будет накапливать тот же заряд q, что и система конденсаторов.
Воспользовавшись формулой (14.23), запишем:
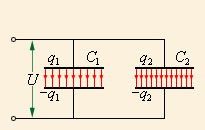
На рисунке 14.41 представлена схема параллельно соединённых конденсаторов. Разность потенциалов между пластинами всех конденсаторов одинакова и равна:
Заряды на пластинах конденсаторов
На эквивалентном конденсаторе ёмкостью Сэкв заряд на пластинах при той же разности потенциалов
Для электроёмкости, согласно формуле (14.23) запишем: CэквU = C1U + C2U + C3U, следовательно, Сэкв = C1+ С2 + С3, и в общем случае 
Различные типы конденсаторов.
В зависимости от назначения конденсаторы имеют различное устройство. Обычный технический бумажный конденсатор состоит из двух полосок алюминиевой фольги, изолированных друг от друга и от металлического корпуса бумажными лентами, пропитанными парафином. Полоски и ленты туго свернуты в пакет небольшого размера.
В радиотехнике широко применяют конденсаторы переменной электроемкости (рис.14.35). Такой конденсатор состоит из двух систем металлических пластин, которые при вращении рукоятки могут входить одна в другую. При этом меняются площади перекрывающихся частей пластин и, следовательно, их электроемкость. Диэлектриком в таких конденсаторах служит воздух.
Значительного увеличения электроемкости за счет уменьшения расстояния между обкладками достигают в так называемых электролитических конденсаторах (рис.14.36). Диэлектриком в них служит очень тонкая пленка оксидов, покрывающих одну из обкладок (полосу фольги). Другой обкладкой служит бумага, пропитанная раствором специального вещества (электролита).
Конденсаторы позволяют накапливать электрический заряд. Электроемкость плоского конденсатора пропорциональна площади пластин и обратно пропорциональна расстоянию между пластинами. Кроме того, она зависит от свойств диэлектрика между обкладками.
Электроемкость. Конденсаторы
Что такое электроемкость проводников
В рамках темы данной статьи нам больше всего интересна такая разность потенциалов между проводниками, когда их заряды противоположны по знаку, но равны друг другу по модулю. В таком случае мы можем ввести новое понятие – электрическая емкость (электроемкость).
Электрической емкостью системы, состоящей из двух проводников, называется отношение заряда одного проводника ( q ) к разности потенциалов между этими двумя проводниками.
Конфигурации и размеры проводников, а также свойства диэлектрика определяют величину электроемкости заданной системы. Наибольший интерес для нас представляют проводники особой формы, называемые конденсаторами.
Конденсатор – это проводник, конфигурация которого позволяет локализовать (сосредотачивать) электрическое поле в одной выделенной части пространства. Проводники, составляющие конденсатор, называются обкладками.
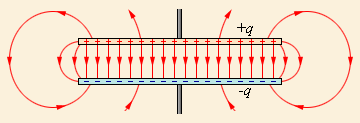
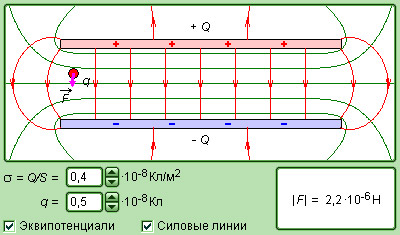
Если мы возьмем две плоские пластины из проводящего материала, расположим их на небольшом расстоянии друг от друга и проложим между ними слой диэлектрика, то мы получим простейший конденсатор, называемый плоским. При его работе электрическое поле будет располагаться преимущественно в промежутке между пластинами, но небольшая часть этого поля будет рассеиваться вокруг них.
Часть электрического поля вблизи конденсатора называется полем рассеяния.
Иногда в задачах мы можем не учитывать его и работать только с той частью электрического поля, которое расположено между обкладками. Однако пренебрегать полем рассеяния допустимо далеко не всегда, поскольку это может привести к ошибочным расчетам из-за нарушения потенциального характера электрического поля.
Модуль напряженности электрического поля, которое создает каждая обкладка в плоском конденсаторе, выражается соотношением следующего вида:
Как рассчитать электроемкость конденсатора
Электрическая емкость плоского конденсатора – величина, обратно пропорциональная расстоянию между обкладками и прямо пропорциональная их площади.
Заполнение пространства между проводниками диэлектрическим материалом может увеличить электроемкость плоского конденсатора в число раз, кратное undefined.
Введем обозначение емкости в виде буквы С и запишем это в виде формулы:
Данная формула называется формулой электроемкости плоского конденсатора.
Конденсаторы бывают не только плоскими. Возможны и другие конфигурации, также обладающие специфическими свойствами.
Обозначим проницаемость диэлектрического материала как ε и запишем формулы, по которым можно найти электрическую емкость конденсаторов:
Как рассчитать электроемкость батареи конденсаторов
Если мы соединим несколько проводников между собой, то мы получим конструкцию, называемую батареей.
С = q 1 + q 2 U или C = C 1 + C 2
Если в батарее конденсаторов элементы соединены параллельно, то для нахождения общей электроемкости нам нужно сложить емкости ее отдельных элементов.
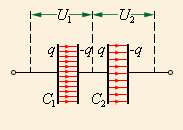
C = q U 1 + U 2 или 1 C = 1 C 1 + 1 C 2
Если конденсаторы в батарее соединены последовательно, то для нахождения общей электроемкости нам нужно сложить величины, обратные емкостям каждого из них.
Справедливость обеих формул, приведенных выше, не зависит от количества конденсаторов в батарее.
где
