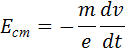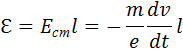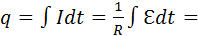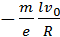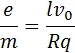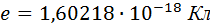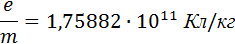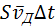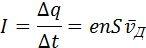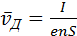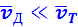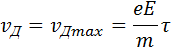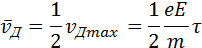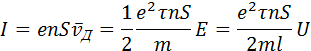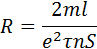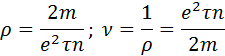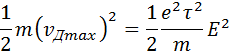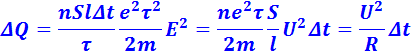Что называется электрическим током в металлах

Электрический ток в металлах

Электрический ток в металлах – это упорядоченное движение электронов под действием электрического поля. Опыты показывают, что при протекании тока по металлическому проводнику переноса вещества не происходит, следовательно, ионы металла не принимают участия в переносе электрического заряда.

Наиболее убедительное доказательство электронной природы тока в металлах было получено в опытах с инерцией электронов. Идея таких опытов и первые качественные результаты (1913 г.) принадлежат русским физикам Л.И. Мандельштаму и Н.Д. Папалекси В 1916 году американский физик Р. Толмен и шотландский физик Б. Стюарт усовершенствовали методику этих опытов и выполнили количественные измерения, неопровержимо доказавшие, что ток в металлических проводниках обусловлен движением электронов.

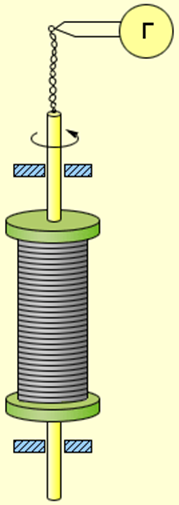
Схема опыта Толмена и Стюарта показана на рис. 1.12.1. Катушка с большим числом витков тонкой проволоки приводилась в быстрое вращение вокруг своей оси. Концы катушки с помощью гибких проводов были присоединены к чувствительному баллистическому гальванометру Г. Раскрученная катушка резко тормозилась, и в цепи возникал кратковременных ток, обусловленный инерцией носителей заряда. Полный заряд, протекающий по цепи, измерялся по отбросу стрелки гальванометра.

Схема опыта Толмена и Стюарта

При торможении вращающейся катушки на каждый носитель заряда e действует тормозящая сила 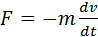которая играет роль сторонней силы, то есть силы неэлектрического происхождения. Сторонняя сила, отнесенная к единице заряда, по определению является напряженностью E_ст поля сторонних сил:

Следовательно, в цепи при торможении катушки возникает электродвижущая сила 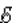, равная

где l – длина проволоки катушки. За время торможения катушки по цепи протечет заряд q, равный

Здесь I – мгновенное значение силы тока в катушке, R – полное сопротивление цепи, υ₀ – начальная линейная скорость проволоки.

Отсюда удельный заряд e / m свободных носителей тока в металлах равен:

Все величины, входящие в правую часть этого соотношения, можно измерить. На основании результатов опытов Толмена и Стюарта было установлено, что носители свободного заряда в металлах имеют отрицательный знак, а отношение заряда носителя к его массе близко к удельному заряду электрона, полученному из других опытов. Так было установлено, что носителями свободных зарядов в металлах являются электроны.

По современным данным модуль заряда электрона (элементарный заряд) равен

а его удельный заряд есть

Хорошая электропроводность металлов объясняется высокой концентрацией свободных электронов, равной по порядку величины числу атомов в единице объема.

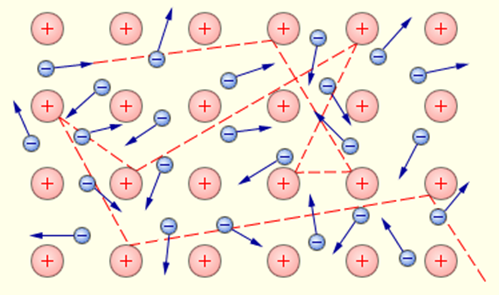
Предположение о том, что за электрический ток в металлах ответственны электроны, возникло значительно раньше опытов Толмена и Стюарта. Еще в 1900 году немецкий ученый П. Друде на основании гипотезы о существовании свободных электронов в металлах создал электронную теорию проводимости металлов. Эта теория получила развитие в работах голландского физика Х. Лоренца и носит название классической электронной теории. Согласно этой теории, электроны в металлах ведут себя как электронный газ, во многом похожий на идеальный газ. Электронный газ заполняет пространство между ионами, образующими кристаллическую решетку металла (рис. 1.12.2).

Газ свободных электронов в кристаллической решетке металла. Показана траектория одного из электронов

Из-за взаимодействия с ионами электроны могут покинуть металл, лишь преодолев так называемый потенциальный барьер. Высота этого барьера называется работой выхода. При обычных (комнатных) температурах у электронов не хватает энергии для преодоления потенциального барьера.

Из-за взаимодействия с кристаллической решеткой потенциальная энергия выхода электрона внутри проводника оказывается меньше, чем при удалении электрона из проводника. Электроны в проводнике находятся в своеобразной «потенциальной яме», глубина которой и называется потенциальным барьером.

Как ионы, образующие решетку, так и электроны участвуют в тепловом движении. Ионы совершают тепловые колебания вблизи положений равновесия – узлов кристаллической решетки. Свободные электроны движутся хаотично и при своем движении сталкиваются с ионами решетки. В результате таких столкновений устанавливается термодинамическое равновесие между электронным газом и решеткой. Согласно теории Друде–Лоренца, электроны обладают такой же средней энергией теплового движения, как и молекулы одноатомного идеального газа. Это позволяет оценить среднюю скорость 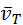теплового движения электронов по формулам молекулярно-кинетической теории. При комнатной температуре она оказывается примерно равной 10 5 м/с.

При наложении внешнего электрического поля в металлическом проводнике кроме теплового движения электронов возникает их упорядоченное движение (дрейф), то есть электрический ток. Среднюю скорость 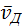дрейфа можно оценить из следующих соображений. За интервал времени Δt через поперечное сечение S проводника пройдут все электроны, находившиеся в объеме

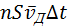
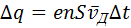
Число таких электронов равно , где n – средняя концентрация свободных электронов, примерно равная числу атомов в единице объема металлического проводника. Через сечение проводника за время Δt пройдет заряд Отсюда следует:

или

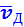
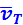
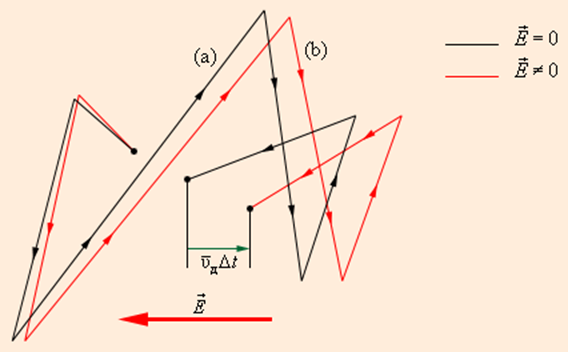
средняя скорость упорядоченного движения электронов в металлических проводниках на много порядков меньше средней скорости их теплового движения

Рис. 1.12.3 дает представление о характере движения свободного электрона в кристаллической решетке.

Движение свободного электрона в кристаллической решетке: а – хаотическое движение электрона в кристаллической решетке металла; b – хаотическое движение с дрейфом, обусловленным электрическим полем. Масштабы дрейфа 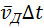сильно преувеличены

Малая скорость дрейфа на противоречит опытному факту, что ток во всей цепи постоянного тока устанавливается практически мгновенно. Замыкание цепи вызывает распространение электрического поля со скоростью c = 3·10 8 м/с. Через время порядка l / c (l – длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля и в ней начинается упорядоченное движение электронов.

В классической электронной теории металлов предполагается, что движение электронов подчиняется законам механики Ньютона. В этой теории пренебрегают взаимодействием электронов между собой, а их взаимодействие с положительными ионами сводят только к соударениям. Предполагается также, что при каждом соударении электрон передает решетке всю накопленную в электрическом поле энергию и поэтому после соударения он начинает движение с нулевой дрейфовой скоростью.

Несмотря на то, что все эти допущения являются весьма приближенными, классическая электронная теория качественно объясняет законы электрического тока в металлических проводниках.

Закон Ома. В промежутке между соударениями на электрон действует сила, равная по модулю eE, в результате чего он приобретает ускорение 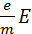. Поэтому к концу свободного пробега дрейфовая скорость электрона равна

где τ – время свободного пробега, которое для упрощения расчетов предполагается одинаковым для всех электронов. Среднее значение скорости дрейфа 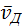равно половине максимального значения:

Рассмотрим проводник длины l и сечением S с концентрацией электронов n. Ток в проводнике может быть записан в виде:

где U = El – напряжение на концах проводника. Полученная формула выражает закон Ома для металлического проводника. Электрическое сопротивление проводника равно:

а удельное сопротивление ρ и удельная проводимость ν выражаются соотношениями:

Закон Джоуля-Ленца.

К концу свободного пробега электроны под действием поля приобретают кинетическую энергию

Согласно сделанным предположениям вся эта энергия при соударениях передается решетке и переходит в тепло.

За время Δt каждый электрон испытывает Δt / τ соударений. В проводнике сечением S и длины l имеется nSl электронов. Отсюда следует, что выделяемое в проводнике за время Δt тепло равно:

Это соотношение выражает закон Джоуля-Ленца.

Таким образом, классическая электронная теория объясняет существование электрического сопротивления металлов, законы Ома и Джоуля–Ленца. Однако в ряде вопросов классическая электронная теория приводит к выводам, находящимся в противоречии с опытом.

Эта теория не может, например, объяснить, почему молярная теплоемкость металлов, также как и молярная теплоемкость диэлектрических кристаллов, равна 3R, где R – универсальная газовая постоянная (закон Дюлонга и Пти, см. ч. I, § 3.10). Наличие свободных электронов на сказывается на величине теплоемкости металлов.

Классическая электронная теория не может также объяснить температурную зависимость удельного сопротивления металлов. Теория дает соотношение 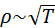, в то время как из эксперимента получается зависимость ρ

T. Однако наиболее ярким примером расхождения теории и опытов является сверхпроводимость.

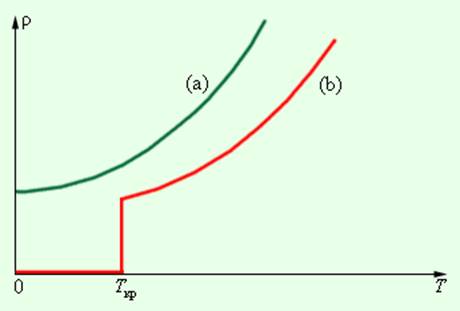
Согласно классической электронной теории, удельное сопротивление металлов должно монотонно уменьшаться при охлаждении, оставаясь конечным при всех температурах. Такая зависимость действительно наблюдается на опыте при сравнительно высоких температурах. При более низких температурах порядка нескольких кельвинов удельное сопротивление многих металлов перестает зависеть от температуры и достигает некоторого предельного значения. Однако наибольший интерес представляет удивительное явление сверхпроводимости, открытое датским физиком Х.Каммерлинг-Онесом в 1911 году. При некоторой определенной температуре T_кр, различной для разных веществ, удельное сопротивление скачком уменьшается до нуля (рис. 1.12.4). Критическая температура у ртути равна 4,1 К, у аллюминия 1,2 К, у олова 3,7 К. Сверхпроводимость наблюдается не только у элементов, но и у многих химических соединений и сплавов. Например, соединение ниобия с оловом (Ni₃Sn) имеет критическую температуру 18 К. Некоторые вещества, переходящие при низких температурах в сверхпроводящее состояние, не являются проводниками при обычных температурах. В то же время такие «хорошие» проводники, как медь и серебро, не становятся сверхпроводниками при низких температурах.

Зависимость удельного сопротивления ρ от абсолютной температуры T при низких температурах: a – нормальный металл; b – сверхпроводник

Вещества в сверхпроводящем состоянии обладают исключительными свойствами. Практически наиболее важным их них является способность длительное время (многие годы) поддерживать без затухания электрический ток, возбужденный в сверхпроводящей цепи.

Классическая электронная теория не способна объяснить явление сверхпроводимости. Объяснение механизма этого явления было дано только через 60 лет после его открытия на основе квантово-механических представлений.

Научный интерес к сверхпроводимости возрастал по мере открытия новых материалов с более высокими критическими температурами. Значительный шаг в этом направлении был сделан в 1986 году, когда было обнаружено, что у одного сложного керамического соединения T_кр = 35 K. Уже в следующем 1987 году физики сумели создать новую керамику с критической температурой 98 К, превышающей температуру жидкого азота (77 К). Явление перехода веществ в сверхпроводящее состояние при температурах, превышающих температуру кипения жидкого азота, было названо высокотемпературной сверхпроводимостью. В 1988 году было создано керамическое соединение на основе элементов Tl–Ca–Ba–Cu–O с критической температурой 125 К.

В настоящее время ведутся интенсивные работы по поиску новых веществ с еще более высокими значениями T_кр. Ученые надеятся получить вещество в сверхпроводящем состоянии при комнатной температуре. Если это произойдет, это будет настоящей революцией в науке, технике и вообще в жизни людей.

Следует отметить, что до настоящего времени механизм высокотемпературной сверхпроводимости керамических материалов до конца не выяснен.

Источник

Электрический ток в металлах: подробное объяснение

Электрический ток в металлах представляет собой упорядоченное движение свободных электронов. Более подробно об этом читайте далее в нашей статье.

Важно знать

Как известно, электрический ток — это упорядоченный поток носителей электрического заряда. Носители — это заряженные частицы, способные свободно перемещаться во всем объеме тела.

В случае металлов этими частицами являются электроны, которые высвобождаются при образовании связи между атомами металла.

Известно, что металлы в твердом состоянии имеют кристаллическую структуру. Частицы в кристаллах расположены в определенном порядке, образуя пространственную решетку (кристалл).

Наконец, кристаллическая решетка металла образована положительными ионами, погруженными в «облако» хаотически движущихся так называемых свободных электронов, также называемых электронами проводимости. В зависимости от валентности атомов металла, один атом может освободить от одного до трех электронов при образовании металлических связей. Число таких высвобожденных электронов непосредственно переводится в число носителей заряда. Это является одним из факторов, влияющих на способность металла проводить электрический ток.

Доказательством того, что ток в металлах вызывается электронами, послужили эксперименты наших отечественных физиков Леонида Исааковича Мандельштама и Николая Дмитриевича Папалекси, а также американских физиков Бальфура Стюарта и Роберта Толмана.

В таблице ниже приведены некоторые примеры удельного сопротивления часто используемых металлов.

Удельное электрическое сопротивление может быть связано с микроскопическими свойствами материала. В частности, он зависит от концентрации носителей заряда и их подвижности.

Движение свободных электронов в металлах не является полностью «свободным», поскольку во время их движении они взаимодействуют с другими электронами, и прежде всего с ионами кристаллической решетки. Специфика этого движения описывается так называемой классической моделью проводимости.

Основные предположения и выводы этой модели представлены в большом упрощении ниже.

Классическая модель проводимости

Без внешнего электрического поля электроны совершают тепловые хаотические движения, сталкиваясь друг с другом, а также сталкиваясь с ионами кристаллической решетки. В результате такого движения среднее положение электронов практически не меняется (см. рис. 1.).

Рис. 1. Пример траектории электрона во время его хаотического теплового движения в металле

Из-за квантовых эффектов, и в частности из-за принципа запрета Паули, который не позволяет всем электронам занимать самое низкое энергетическое состояние, средняя скорость электронов в металлах, связанная с их хаотическим тепловым движением, больше, чем скорость частиц в классическом идеальном газе той же температуры. Она составляет порядка 10 м/с.

Если электрическое напряжение U приложено к концам проводника длиной L в нем появится электрическое поле с напряженностью E = U / L

Под действием этого внешнего поля, согласно второму закону динамики, электроны ускоряются: a = F / m,

Ускоренное движение электрона длится лишь довольно короткое время, пока он не столкнется с ионом
кристаллической решетки. В результате такого столкновения электрон теряет практически всю свою кинетическую энергию. Однако замедленный электрон не остается в состоянии покоя — он снова ускоряется под действием электрического поля, снова сталкивается с одним из ионов из ионы кристаллической решетки и т.д. Этот эффект добавляет к скорости тепловых движений дополнительную направленную среднюю скорость u, которая из-за отрицательного заряда электрона имеет направление, противоположное напряженности внешнего электрического поля. Эта скорость называется средней скоростью дрейфа (рис. 2).

Рис. 2. Дрейф электрона под действием внешнего электрического поля

В проводнике начинает течь электрический ток с силой тока I (см. рисунок 3).

Из полученной формулы следует, что скорость дрейфа, помимо внешнего электрического поля, определяется средним интервалом времени между столкновениями электронов с ионами решетки. Этот параметр зависит от многих факторов (включая температуру, кристаллическую структуру металла, дефекты кристаллической структуры, примеси) и, как выясняется, существенно влияет на электрическое сопротивление материала.

Классическая теория проводимости достаточно хорошо описывает явление электропроводности в металлах. Однако эта теория не может объяснить экспериментально наблюдаемую зависимость электрического сопротивления от температуры.

Причина упомянутой неудачи классической теории проводимости заключается в том, что она не учитывает влияние ионов решетки на движение электронов между столкновениями. Более близкие к реальности результаты дает квантовая теория проводимости, которая описывает электроны как частицы, подверженные квантовой статистике, движущиеся в периодическом электрическом поле, создаваемом положительными ионами решетки.

Выводы простым языком

Отрицательный заряд всех свободных электронов по абсолютному значению равен положительному заряду всех ионов решётки. Поэтому в обычных условиях металл электрически нейтрален. Свободные электроны в нём движутся беспорядочно. Но если в металле создать электрическое поле, то свободные электроны начнут двигаться направленно под действием электрических сил. Возникнет электрический ток. Беспорядочное движение электронов при этом сохраняется, подобно тому как сохраняется беспорядочное движение в стайке мошкары, когда под действием ветра она перемещается в одном направлении.

« Скорость движения самих электронов в проводнике под действием электрического поля невелика — несколько миллиметров в секунду, а иногда и ещё меньше. Но как только в проводнике возникает электрическое поле, оно с огромной скоростью, близкой к скорости света в вакууме (300 000 км/c), распространяетcя по всей длине проводника. »

Перышкин А. В. Физика 8. – М.: Дрофа, 2010

Как пример, электрический сигнал, посланный, например, по проводам из Москвы во Владивосток (s = 8000 км), приходит туда примерно через 0,03 с.

Одновременно с распространением электрического поля все электроны начинают двигаться в одном направлении по всей длине проводника. Так, например, когда цепь электрической лампы замкнута, электроны в спирали лампы также движутся упорядоченно.

Сравнение электрического тока с потоком воды в водопроводной системе и распространения электрического поля с распространением давления воды поможет нам понять это. Когда вода поднимается в резервуар для воды, давление (напор) воды очень быстро распространяется по всей системе водоснабжения. Когда мы включаем кран, вода уже находится под давлением и сразу же начинает течь. Но вода, которая была в кране, течет, а вода из башни достигает крана гораздо позже, потому что вода движется с меньшей скоростью, чем распространяется давление.

Когда говорят о скорости распространения электрического тока в проводнике, то имеют в виду скорость распространения по проводнику электрического поля.

Источник

Электрический ток в металлах

Содержание:

Электрический ток — это направленное (упорядоченное) движение частиц или квазичастиц — носителей электрического заряда. Такими носителями могут являться: в металлах — электроны, в электролитах — ионы (катионы и анионы), в газах — ионы и электроны, в вакууме при определённых условиях — электроны, в полупроводниках — электроны или дырки (электронно-дырочная проводимость).

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Электрический ток в металлах

Электрический ток в металлах – это упорядоченное движение электронов под действием электрического поля. Наиболее убедительное доказательство электронной природы тока в металлах было получено в опытах с инерцией электронов (опыт Толмена и Стьюарта)

Подвижные носители зарядов и электрический ток

Когда проводник помещают в электрическое поле, подвижные носители зарядов в проводнике перемещаются под действием поля, что приводит к выравниванию потенциалов всех точек проводника (§ 15.8). Однако если у двух точек проводника каким-то образом искусственно поддерживать разные потенциалы, то внутри проводника будет существовать поле. Это поле будет создавать непрерывное движение зарядов. Положительные заряды при этом движутся от точек с большим потенциалом к точкам с меньшим потенциалом, а отрицательные — наоборот.

Направленное движение свободных зарядов в проводнике под действием сил поля называется электрическим током проводимости или электрическим током. Подвижными носителями зарядов в любых проводниках являются свободные электроны или ионы. Отметим, что движение отдельного заряда в проводнике иногда называют микротоком, а полный ток — макротоком.

При движении в вакууме свободные носители зарядов (одного знака) не встречают никакого противодействия и приобретают кинетическую энергию за счет работы сил электрического поля. Когда же ток проходит в веществе, движущиеся заряды встречают противодействие, поскольку взаимодействуют с другими зарядами и частицами, входящими в состав вещества. (Например, электроны в металле, сталкиваясь о ионами решетки, теряют энергию, сообщенную им полем.) При этом увеличивается интенсивность хаотического движения частиц вещества, т. е. происходит нагревание вещества. Таким образом, ток в веществе всегда сопровождается увеличением внутренней энергии вещества.

Сила тока и плотность тока в проводнике

Если в вакууме движение зарядов под действием поля происходит с непрерывно нарастающей скоростью, то в твердых веществах и в жидкостях дело обстоит иначе.

Подобно тому, как поезд движется с постоянной скоростью, когда сила тяги равна силе сопротивления окружающей среды, средняя скорость направленного движения подвижных носителей зарядов при постоянной напряженности поля Е в проводнике пропорциональна напряженности поля Е:

Коэффициент пропорциональности и, который выражает зависимость скорости движения носителей зарядов, обусловленной действием сил поля, от рода вещества проводника и внешних условий, называют подвижностью носителей тока. Подвижность измеряется скоростью направленного движения носителей тока в проводнике при напряженности поля, равной единице. (Покажите, что единицей подвижности зарядов в СИ является

Если в проводнике течет электрический ток, то через сечение проводника , перпендикулярное линиям напряженности поля, проходят подвижные носители зарядов подобно тому, как мимо наблюдателя, стоящего у обочины дороги, проезжают автомашины. Величину , характеризующую быстроту переноса заряда в проводнике через его поперечное сечение, называют силой тока (или током). Силу тока в проводнике измеряют количеством электричества, проходящего через поперечное сечение проводника за единицу времени:

Величину , характеризующую быстроту переноса заряда в проводнике через единицу площади его поперечного сечения, называют плотностью тока. При равномерном распределении потока зарядов по всей площади сечения проводника плотность тока

Если поток зарядов распределяется по площади поперечного сечения проводника неравномерно, то всегда можно выбрать столь малую часть площади сечения , чтобы поток зарядов через нее можно было считать равномерным. Тогда, если сила тока через выбранную площадку равна , то плотность тока в этом месте поперечного сечения равна

Выясним, чем определяется плотность тока в проводнике. Предположим, что линии напряженности поля перпендикулярны плоскости поперечного сечения проводника, а все носители тока заряжены положительно и имеют одинаковый заряд . Пусть напряженность поля в проводнике Е, количество подвижных носителей зарядов в единице объема проводника , а скорость их направленного движения в проводнике . Выделим внутри проводника цилиндр, образующая которого параллельна Е, а площадь сечения равна (рис. 16.1). Тогда внутри цилиндра будет находиться носителей тока, а их общий заряд будет равен .

За время все эти носители тока пройдут через переднее основание цилиндра. При этом ток через поперечное сечение цилиндра будет равен , а плотность тока

или в векторной форме

Поскольку , получим

Так как напряженность поля Е есть вектор, а и — скалярные величины, то плотность тока является вектором, направление которого совпадает с направлением вектора Е. Таким образом, за направление тока условно принимается направление движения положительных зарядов в проводнике. Поскольку , то

Напряженность поля в цилиндре можно выразить по формуле (15.14):

Тогда из (16.6) и (16.7) получим

Эти формулы можно применять и к проводнику произвольных размеров, тогда будет обозначать длину всего проводника, — площадь его поперечного сечения, а — напряжение на его концах.

Такой ток, при котором плотность тока в каждой точке проводника не изменяется со временем, называют постоянным. Из (16.7 а) видно, что постоянный ток существует в проводнике только при постоянном напряжении на концах проводника. Если же ток изменяется со временем, то его называют переменным. Все изложенное ниже в этом разделе относится к постоянному току.

Подчеркнем еще раз, что за направление тот принято направление движения положительных зарядов, которое совпадает с направлением электрического поля. Отрицательно заряженные носители тока, как мы знаем, под действием сил поля движутся в направлении, противоположном направлению поля. Однако перемещение в проводнике отрицательных зарядов в каком-либо направлении эквивалентно перемещению таких же по величине положительных зарядов в противоположном направлении. Следовательно, направление тока, созданного отрицательно заряженными носителями, также совпадает с направлением поля. При этом плотность тока и сила тока определяются выражениями, аналогичными (16.6 а) и (16.7 а). В этих формулах следует отбросить знак заряда, и тогда они будут применимы и для положительных, и для отрицательных зарядов:

Чтобы установить, какие заряды в металлах являются свободными, был выполнен следующий опыт. Металлический провод большой длины наматывали на цилиндрический каркас, а концы провода соединяли с двумя кольцами (рис. 16.2), к которым были прижаты угольные пластинки, присоединенные к гальванометру (прибору для измерения слабых токов).

Катушку с проводом приводили в быстрое вращение, а затем резко тормозили. В этот момент стрелка гальванометра отклонялась, т. е. возникал кратковременный ток. Его появление объясняется следующим образом.

При вращении катушки вместе с проводником двигались и носители тока в проводнике. Когда катушку резко останавливали, то носители тока некоторое время продолжали свое движение по инерции, т. е. в проводнике создавался кратковременный ток. По направлению этого тока было установлено, что движутся отрицательные заряды, а более подробные исследования показали, что подвижными носителями зарядов в металлах являются электроны.

Замкнутая электрическая цепь

Кратковременный электрический ток в проводнике можно получить,, соединяя проводником два заряженных проводящих тела, которые имеют различный потенциал. Ток в проводнике исчезает, когда потенциал тел становится одинаковым. Напомним, что вообще ток в проводнике ослабляет поле внутри него и выравнивает потенциал всех точек проводника (§ 15.8).

Для получения длительного тока нужно замкнуть цепь из проводников, чтобы заряды могли циркулировать по этой цепи. Кроме того, в проводниках нужно поддерживать электрическое поле, которое ток стремится уничтожить. Поле внутри проводников, составляющих замкнутую цепь, должен поддерживать источник электрической энергии.

В цепь включают также потребители электрической энергии, в которых ток выполняет полезную работу. Кроме того, в цепь включают соединительные провода и выключатель (рубильник) для замыкания и размыкания цепи. Заметим, что приборы, предназначенные для включения в цепь должны иметь зажимы (клеммы), к которым присоединяют подводящие провода. Следовательно, простая электрическая цепь состоит из источника электрической энергии, потребителя, подводящих проводов и выключателя.

Электродвижущая сила источника электрической энергии

Выше было показано, что работа сил электрического поля при перемещении заряда по замкнутому контуру равна нулю (§ 15.5). Это означает, что если в замкнутой цепи на заряды действуют одни только электрические силы, то работу с помощью тока получить нельзя. Следовательно, в электрической цепи должен быть хотя бы один такой участок, в котором на подвижные носители зарядов, кроме сил электрического поля, действовали бы еще какие-либо другие силы, способные совершить работу по перемещению этих зарядов. Такие силы называют сторонними.

Представим себе два заряженных проводника А и В (рис. 16.3).

Допустим, что потенциал проводника А больше, чем потенциал проводника В. Если соединить их проводником АСВ, то положительные заряды под действием сил электрического поля устремятся от А к В по проводнику АСВ. Однако это движение очень скоро прекратится, так как потенциалы проводников А и В станут равными. Чтобы этого не произошло и движение носителей тока продолжалось достаточно долго, необходимо положительные заряды из точки В каким-то образом переносить снова в точку А, например, по проводнику ВDА. Но такое перемещение зарядов самопроизвольно происходить не может, так как силы электрического поля действуют на них в противоположную сторону.

Следовательно, в проводнике ВDА на заряды должны действовать сторонние силы направленные против сил электрического поля и превышающие их по величине. Тогда на участке АСВ носители тока будут двигаться под действием сил электрического поля от А к В, а на участке ВDА — под действием поля сторонних сил от В к А. В этом случае в замкнутой цепи будет непрерывно циркулировать поток зарядов, т. е. будет идти электрический ток, а потенциалы проводников А и В не смогут выравняться.

Сторонние силы будут совершать работу по перемещению подвижных носителей зарядов на участке ВDА, преодолевая противодействие электрического поля и частиц вещества, из которого сделан проводник ВDА. За счет работы, выполненной сторонними силами против сил электрического поля, ток совершает работу на участке цепи АСВ.

Таким образом, на участке ВDА электрическая энергия получается за счет других видов энергии, а на участке АСВ, наоборот, электрическая энергия будет превращаться в другие виды энергии, например во внутреннюю энергию проводника. Поэтому участок цепи, в котором заряды движутся в сторону действия сторонних сил, называют источником электрической энергии (участок ВDА), а участок, в котором заряды движутся в сторону действия электрических сил называют потребителем электрической энергии.

Отметим, что в электротехнике источники электрической энергии называют генераторами. Те из них, в которых химическая энергия превращается в электрическую, называют гальваническими элементами или аккумуляторами.

Величину, характеризующую зависимость электрической энергии, приобретенной зарядом в генераторе, от внутреннего устройства последнего, называют электродвижущей силой генератора и обозначают э. д. с. или . Электродвижущую силу генератора измеряют работой сторонних сил, выполненной при перемещении единичного положительного заряда:

(Покажите, что единицей э.д.с. в СИ является 1 В.)

Итак, длительный ток может идти в замкнутой цепи только при наличии в ней э.д.с. Если убрать проводник АСВ (рис. 16.3), то в результате перемещения зарядов на участке ВDА под действием сторонних сил в точке А будут накапливаться положительные заряды, а в точке В — отрицательные. Напряжение между проводниками A и В будет увеличиваться до тех пор, пока электрические и сторонние силы, действующие на заряды, не сравняются. Тогда накопление зарядов в точках A и В прекратится, а напряжение между A и В достигнет максимального значения для данного генератора. (Объясните, почему напряжение на генераторе при разомкнутой цепи равно его э. д. с.)

Таким образом, чтобы измерить э. д. с. генератора, нужно присоединить к нему вольтметр при разомкнутой, цепи.

Внешняя и внутренняя части цепи

В предыдущем параграфе было показано, что электрическая цепь имеет две существенно различные части. Часть цепи, в которой заряды движутся по направлению действия электрических сил (АСВ на рис. 16.3), называют внешней, а часть цепи, в которой заряды движутся в сторону действия сторонних сил (ВDА на рис. 16.3), называют внутренней. Иначе говоря, внутренней цепью является источник электрической энергии, а внешней — вся остальная часть цепи.

Те точки, в которых внешняя цепь граничит с внутренней, называют полюсами. Во внешней цепи заряды движутся из одной точки в другую только при наличии разности потенциалов; поэтому, когда в замкнутой цепи идет ток, потенциал во внешней цепи от точки к точке уменьшается (в направлении от A к В на рис. 16.3). Таким образом, у одного из полюсов имеется самый большой потенциал, а у другого — самый маленький потенциал по сравнению с другими точками цепи. Полюс с наибольшим потенциалом называют положительным и обозначают знаком «+», а полюс с наименьшим потенциалом называют отрицательным и обозначают знаком «—».

В схемах электрических цепей применяются условные обозначения, показанные на рис. 16.4.

Принято считать, что тонкая длинная черта в обозначении источника электрической энергии является положительным полюсом, а короткая толстая — отрицательным.

Схема простой электрической цепи с включением измерительных приборов показана на рис. 16.5.

Напомним, что за направление тока во внешней цепи принимают движение положительных зарядов от положительного полюса к отрицательному (§ 16.2), а во внутренней —отрицательного полюса к положительному, хотя в металлах электроны движутся в обратную сторону.

Поскольку во внешней цепи по направлению тока потенциал от точки к точке падает, напряжение на любом участке, составляющем часть внешней цепи (рис. 16.5), меньше, чем напряжение на полюсах источника, т. е. на всей внешней цепи. Заметим, что это справедливо только при наличии тока в цепи. Если цепь разомкнуть, то потенциал всех точек проводника, соединенного с одним из полюсов, будет один и тот же. (Подумайте, существует ли при этом напряжение между полюсами.)

Закон Ома для участка цепи без ЭДС

Сопротивление проводника. Падение напряжения. Когда по какому-либо участку цепи протекает ток, то между силой тока и напряжением для этого участка существует определенная функциональная зависимость, которую называют вольтамперной характеристикой.

Для металлического проводника вольтамперная характеристика выражается формулой (16.76):

Отсюда видно, что между и должна быть прямо пропорциональная зависимость. Эту зависимость впервые установил опытным путем немецкий ученый Г. Ом.

Наглядным изображением вольтамперной характеристики является график зависимости от , который для проводника, как следует из формулы (16.7 6), представляет собой прямую линию (рис. 16.6).

Эту зависимость можно выразить формулой

где коэффициент пропорциональности

Ветчину , выражающую зависимость силы тока в проводнике от его рода, размеров и внешних условий, называют проводимостью участка цепи. Проводимость измеряется силой тока, возникающей в проводнике при напряжении на его концах, равном единице.

На практике соотношение (16.9) чаще записывают в виде

Величину R называют электрическим сопротивлением. Аналогично тому, как трение в механике создает противодействие движению тел, сопротивление проводника создает противодействие направленному движению зарядов и определяет превращение электрической энергии во внутреннюю энергию проводника.

Величина, характеризующая противодействие электрическому току в проводнике, которое обусловлено внутренним строением проводника и хаотическим движением его частиц, называется электрическим сопротивлением проводника. Сопротивление участка цепи (без э. д. с.) измеряется напряжением на этом участке, необходимым для получения в нем тока, равного единице.

Выведем единицу сопротивления R в СИ:

В СИ за единицу сопротивления принимается ом (Ом). Омом называется сопротивление такого участка цепи без э. д. е., по которому течет ток в 1 А при напряжении на его концах в 1 В *).

*) За единицу проводимости в СИ принят симено (См): 1.

Закономерность, найденная Омом для металлических проводников, выражается формулой (16.11) и называется законом Ома для участка цепи без э. д. c.: сила тока на участке цепи без э. д. с. прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению: .

Перепишем формулу закона Ома следующим образом:

Физический смысл этого выражения заключается в том, что — это полная работа, совершаемая электрическим полем при перемещении единичного заряда на данном участке цепи, т. е. израсходованная электрическая энергия на участке цепи при перемещении по нему единичного заряда. На участке цепи без э. д. c., обладающем сопротивлением R, вся эта энергия идет на нагревание проводника, т. е. превращается в его внутреннюю энергию. Подчеркнем еще раз, что это превращение энергии обусловлено сопротивлением, которое действует аналогично трению в механических процессах.

Считая, что на участке цепи энергия отданная равна энергии полученной, можно рассматривать (16.116) как выражение закона сохранения энергии для участка цепи. Поэтому можно сказать, что произведение IR, которое называют падением напряжения, выражает увеличение внутренней энергии участка цепи, т. е. численно равно электрической энергии, затраченной на тепловое действие в этом участке цепи при прохождении по нему единичного заряда.

В подводящих проводах, по которым идет ток от генератора к потребителю, всегда существует падение напряжения. Именно поэтому напряжение, у потребителя всегда меньше, чем на полюсах генератора. Падение напряжения в подводящих проводах иногда называют еще потерей напряжения.

Заметим еще, что устройства, которые включают в электрическую цепь для ограничения тока, называют резисторами.

Зависимость сопротивления от материала, длины и площади поперечного сечения проводника

Выясним, чем определяется сопротивление металлического проводника. В металле подвижными носителями зарядов являются свободные электроны. Можно считать, что при своем хаотическом движении они ведут себя подобно молекулам газа. Поэтому в классической физике свободные электроны в металлах называют электронным газом и в первом приближении считают, что к нему применимы законы, установленные для идеального газа.

Плотность электронного газа и строение кристаллической решетки зависят от рода металла. Поэтому сопротивление проводника должно зависеть от рода его вещества. Кроме того, оно должно еще зависеть от длины проводника, площади его поперечного сечения и от температуры.

Влияние сечения проводника на его сопротивление объясняется тем, что при уменьшении сечения поток электронов в проводнике при одной и той же силе тока становится более плотным, поэтому и взаимодействие электронов с частицами вещества в проводнике становится сильнее. Покажем это более строго.

Поскольку то

Из этой формулы видно, что сопротивление проводника прямо пропорционально его длине и обратно пропорционально площади его поперечного сечения. Величину , характеризующую зависимость сопротивления проводника от материала, из которого он сделан, и от внешних условий, называют удельным сопротивлением вещества. (Покажите, что единицей удельного сопротивления в СИ является 1 Ом . м.) Удельное сопротивление различных веществ при расчетах берут из таблиц.

Величину, обратную удельному сопротивлению, называют удельной проводимостью вещества и обозначают :

(Покажите, что единицей удельной проводимости в СИ является 1 См/м.)

Зависимость сопротивления от температуры

Поскольку при нагревании вещества хаотическое движение его частиц становится интенсивнее, возрастает противодействие направленному движению носителей тока. Это видно из формулы (16.14): .

При нагревании металлического проводника подвижность носителей тока и уменьшается, а и е остаются постоянными. Следовательно, должно при этом возрастать. Опыт показал, что в широком интервале температур приращение удельного сопротивления металла прямо пропорционально приращению температуры. Если удельное сопротивление при 0°С обозначить через , а при температуре t — через то , или

Величину , характеризующую зависимость изменения удельного сопротивления при нагревании от рода вещества, называют температурным коэффициентом сопротивления. Температурный коэффициент сопротивления измеряют числом, показывающим, на какую часть своей величины, взятой при О °С, изменятся удельное сопротивление при нагревании на 1 °С:

Выведем формулу для расчета сопротивления проводников при различных температурах. Из (16.17) имеем

Подставляя это значение в (16.15), окончательно получим

Зависимость сопротивления металлов от температуры используется в термометрах сопротивления. Они позволяют измерять температуру с точностью до тысячных долей градуса (поскольку сопротивление можно измерять с высокой точностью). Отметим еще, что коэффициент а для угля и электролитов, а также для чистых полупроводников отрицателен, так как их сопротивление при нагревании уменьшается (§§ 19.1 и 21.2).

Сверхпроводимость

Зависимость сопротивления от температуры, оказывается, не всегда можно выражать формулой (16.18). При низких температурах были обнаружены интересные отклонения от этой зависимости. При приближении температуры некоторых проводников из чистых металлов к абсолютному нулю их сопротивление стремится не к нулю, как следует из (16.18), а к некоторому предельному значению, отличному от нуля.

Измеряя сопротивления проводников при очень низких температурах, голландский физик X. Камерлинг-Оннес в 1911 г. обнаружил явление, названное в дальнейшем сверхпроводимостью. Оказалось, что в некоторых случаях при достаточно низкой температуре сопротивление вещества скачком падает до нуля (рис. 16.7).

Если из такого вещества сделать замкнутую цепь (например, кольцо) и возбудить в ней ток, то он будет циркулировать в цепи сколь угодно долгое время, так как носители тока не будут терять своей энергии на нагревание проводника.

Для получения сверхпроводимости нужно иметь вещество с правильной кристаллической решеткой. Посторонние примеси и дефекты решетки нарушают сверхпроводимость, и такие проводники даже при температуре, близкой к абсолютному нулю, имеют некоторое сопротивление.

Сверхпроводимость позволяет получать при низких температурах в проводниках небольшого сечения огромные токи. Поэтому из сверхпроводников (сплавы ниобий — титан, ниобий — олово и др.) изготавливаются обмотки мощных электрических генераторов и сверхмощных электромагнитов, которые охлаждаются жидким гелием до 4 К. Разрабатываются сверхпроводящие кабели для передачи электроэнергии.

Эквивалентное сопротивление

Пусть между точками A и В (рис. 16.8, а) включено несколько потребителей, соединенных произвольным образом. Допустим, что общий ток у этих потребителей равен , а напряжение между точками A и В равно . Представим теперь, что все потребители между точками A и В отключены и вместо них включен один проводник с сопротивлением R (рис. 16.8, б). Сопротивление этого проводника можно подобрать так, чтобы показания амперметра и вольтметра остались прежними. Очевидно, что такая замена не вызовет изменений во всех остальных участках замкнутой цепи (не показанных на рисунке). Это означает, что сопротивления между точками A и В на обеих схемах равноценны.

Сопротивление, при включении которого вместо всех других проводников, находящихся между двумя точками цепи, ток и напряжение остаются неизменными, называют эквивалентным сопротивлением этих проводников.

Последовательное соединение потребителей энергии тока

Последовательное соединение потребителей изображено на рис. 16.9. Расчет токов, напряжений и сопротивлений при таком соединении делают с помощью правил, приведенных ниже.

1. При последовательном соединении сила тока во всех участках цепи одинакова:

Все амперметры на рис. 16.9 показывают одинаковую силу тока.

Объясняется это тем, что заряды в цепи не создаются и не уничтожаются. Индекс у обозначения силы тока при последовательном соединении ставить нет смысла.

2. При последовательном соединении напряжение на внешней цепи равно сумме напряжений на отдельных участках цепи:

Это можно установить из опытов по показаниям вольтметров. (Объясните соотношение (16.20) на основании закона сохранения энергии.)

3. Напряжения на отдельных участках цепи при последовательном соединении прямо. пропорциональны сопротивлениям участков:

(Докажите это с помощью закона Ома и соотношения (16.19).)

4. При последовательном соединении эквивалентное сопротивление всей цепи равно сумме сопротивлений отдельных участков цепи:

Выведите это соотношение с помощью закона Ома и формулы (16.20).)

Из соотношения (16.20) видно, что при последовательном соединении п одинаковых участков цепи общее напряжение равно

где —напряжение на одном участке. Аналогично из (16.22) получаем

Отметим, что при размыкании цепи у одного из последовательно соединенных потребителей ток исчезает во всей цепи. Поэтому последовательное соединение на практике не всегда удобно.

Параллельное соединение потребителей энергии тока

Параллельное соединение потребителей изображено на рис. 16.10. Отметим, что точка, в которой сходится больше двух проводников, называется узлом (В и С на рис. 16.10).

Все вместе параллельно соединенные проводники составляют разветвление, а каждый из них называется ветвью. При параллельном соединении потребителей для расчета токов, напряжений и сопротивлений пользуются тоже четырьмя правилами.

1. При параллельном соединении напряжения на отдельных ветвях и на всем разветвлении одинаковы:

2. Ток до и после разветвления равен сумме токов в отдельных ветвях:

Это можно установить по показаниям амперметров. (Объясните правило (16.26), основываясь на законе сохранения заряда.)

3. Токи в отдельных ветвях разветвления обратно пропорциональны сопротивлениям этих ветвей:

(Выведите это соотношение с помощью закона Ома и формулы (16.25).)

4. Проводимость всего разветвления равна сумме проводимостей отдельных ветвей:

(Выведите это соотношение с Помощью закона Ома и формулы (16.26).)

Отметим, что эквивалентное сопротивление разветвления всегда меньше самого маленького из сопротивлений составляющих его ветвей. В случае, когда все ветви в разветвлении одинаковы, общий ток в цепи будет

где — сила тока в одной ветви, a m — число ветвей. Эквивалентное сопротивление разветвления

Если напряжение между узлами остается постоянным, то токи в ветвях не зависят друг от друга. Из этого следует, что в большинстве случаев на практике для потребителей удобно использовать параллельное соединение.

Закон Ома для всей цепи

Пусть к источнику электрической энергии с электродвижущей силой присоединена внешняя цепь, в которой идет ток I, а вольтметр, соединенный G полюсами источника, показывает напряжение на внешней цепи (рис. 16.11, а).

Источник электрической энергии является проводником и всегда имеет некоторое сопротивление, поэтому ток выделяет в нем тепло. Это сопротивление r называют внутренним сопротивлением источника. На основании закона сохранения энергии можно сделать следующее заключение.

Электродвижущая сила численно равна энергии, полученной единичным электрическим зарядом во внутренней цепи, а напряжение равно той энергии, которую он теряет во внешней цепи. Кроме того, этот заряд теряет во внутренней цепи энергию Ir, которая идет на выделение тепла в источнике электрической энергии. Так как энергия в цепи не возникает и не исчезает, то сколько энергии заряд получает, столько же и теряет, пройдя всю замкнутую цепь. Поэтому

Если внешняя цепь состоит из неподвижных металлических проводников, эквивалентное сопротивление которых R то , так как в этом случае вся электрическая энергия расходуется на тепловое действие. Заменяя в (16.31) напряжение через , получаем

Это соотношение называют законом Ома для всей цепи: сила тока в электрической цепи с одной э. д. с. прямо пропорциональна электродвижущей силе и обратно пропорциональна сумме сопротивлений внешней и внутренней цепей.

Если пользоваться определенным источником электрической энергии, то и r в соотношении (16.31) можно считать постоянными величинами. Внешнюю цепь к этому источнику можно присоединять с разными сопротивлениями R. В зависимости от этого будут получаться различные значения тока и напряжения . Так как при этом сумма остается постоянной, то при увеличении должно уменьшаться , и наоборот.

Итак, чем больше сопротивление внешней цепи R, тем больше энергии единичный заряд расходует во внешней цепи и меньше во внутренней (r уменьшается).

Когда R велико по сравнению с r, падение напряжения во внутренней цепи так мало по сравнению с , что им можно пренебречь. Таким образом, при большом сопротивлении R напряжение на внешней цепи приближенно равно э. д. c.:

На этом основано измерение э. д. c., описанное в § 16.4. Действительно, когда внешней цепи нет, то источник электрической энергии замкнут на вольтметр (рис. 16.11,6), который показывает падение напряжения R на самом себе, равное . А так как сопротивление вольтметра очень велико (§22.17), то при этом справедливо соотношение (16.33).

Соединение одинаковых источников электрической энергии в батарею

При получении электрической энергии от гальванических элементов и аккумуляторов часто приходится соединять их в батарею. Соединяют элементы последовательно, параллельно и смешано.

При последовательном соединении элементов в батарею положительный полюс предыдущего источника соединяется с отрицательным полюсом последующего (рис. 16.12). Применяя к батарее формулу (16.32 а), следует помнить, что для этого случая под подразумевается э. д. с. всей батареи , а под r — внутреннее сопротивление батареи . Таким образом, формула (16.32 а) принимает вид

На практике всегда соединяют в батарею одинаковые элементы.

При последовательном соединении п элементов заряд под действием сторонних сил приобретает энергию поочередно во всех п элементах. Поэтому э. д. с. батареи будет равна где — э. д. с. одного элемента. Если внутреннее сопротивление одного элемента r, то сопротивление батареи будет равно , так как заряд поочередно преодолевает сопротивление всех элементов. Следовательно, закон Ома для всей цепи при последовательном соединении элементов имеет вид

Как видно из этой формулы, последовательное соединение элементов дает значительное увеличение тока в том случае, когда внутреннее сопротивление одного элемента много меньше сопротивления внешней цепи R.
При параллельном соединении элементов в батарею все их положительные полюсы присоединяются к одной клемме, а отрицательные — к другой (рис. 16.13). В этом случае заряды, которые проходят через один элемент, не попадают в другие, т. е. э. д. с. батареи равна э. д. с. одного элемента , а внутреннее сопротивление батареи из т одинаковых элементов равно . Таким образом, закон Ома для всей цепи при параллельном соединении имеет вид

(Подумайте, почему целесообразно соединять элементы параллельно в том случае, когда внутреннее сопротивление одного элемента много больше, чём сопротивление внешней цепи.)

Смешанное соединение элементов изображено на рис. 16.14.

В этом случае увеличение э. д. с. дает только последовательное соединение, т. е. . Учитывая, что последовательное соединение увеличивает сопротивление, а параллельно уменьшает, имеем . Таким образом, закон Ома для всей цепи при смешанном соединении имеет вид

Смешанное соединение выгодно применять, когда сопротивление внешней цепи близко к сопротивлению одного элемента.

Закон Ома для участка цепи с ЭДС и для всей цепи при нескольких ЭДС

Сторонние силы могут действовать одновременно во многих участках замкнутой цепи, в том числе и у потребителя. Поэтому э. д. с. имеется не только в генераторе, но и во всех тех участках цепи, в которых действуют сторонние силы.

Когда заряды на участке цепи движутся по направлению действия на них сторонних сил, э. д. с. участка считается положительной. На этом участке обязательно происходит превращение в электрическую энергию других видов энергии. Если же заряды движутся в сторону, противоположную направлению действия на них сторонних сил, э. д. с. считается отрицательной. В этом случае электрические заряды теряют свою энергию, преодолевая противодействие сторонних сил. Электродвижущую силу на таком участке цепи принято называть противо-э. д. с.

Вспомним, что, преодолевая сопротивление, заряды теряют свою энергию, которая превращается во внутреннюю энергию-проводника, т. е. идет на его нагревание. Аналогично, преодолевая противодействие сторонних сил На участке цепи с отрицательной э. д. c., заряды теряют свою энергию, которая превращается в другие виды энергии, отличные от внутренней энергии. Итак, наличие э. д. с. на участке цепи обеспечивает либо превращение в электрическую энергию других видов энергии (в генераторе), либо превращение электрической энергии в другие виды (кроме внутренней энергии) при отрицательной э. д. с. Например, при работе электродвигателя наличие противо-э. д. с. обусловливает превращение электрической энергии в механическую.

Обобщим все изложенное. Когда на участке цепи действуют сторонние силы, то возможны три различных случая:

Первый случай относится к генератору, т. е. к участку цепи, который снабжает электрической энергией другие участки цепи. Его э. д. с. численно равна электрической энергии, приобретенной единичным зарядом. Если R есть сопротивление всего этого участка (включая сюда и внутреннее сопротивление генератора r), а — напряжение на нем, то, когда по нему течет ток I,

Действительно, на основании закона сохранения энергии можно утверждать, что если единичный заряд получил на участке энергию и потерял на нем же энергию на тепловое действие, то у него остается энергия . Эту энергию заряд передает в цепь, присоединенную к генератору. Определив I из (16.37), получим закон Ома для участка цепи, являющегося генератором:

Заметим, что эта формула применима при любой присоединенной к генератору цепи.

Второй случай наблюдают при зарядке аккумулятора и при работе электродвигателя. Электрическая энергия, израсходованная единичным зарядом на таком участке, определяется напряжением (рис. 16.15).

Если сопротивление всего этого участка, а ток в нем I, то энергия, израсходованная в нем единичным зарядом на тепловое действие, равна , а энергия, превратившаяся в другие виды, равна . Таким образом, на основании закона сохранения энергии имеем

откуда получаем закон Ома для участка цепи с противо-э.д.c.:

В третьем случае электрические и сторонние силы направлены в одну сторону. Поэтому заряды будут двигаться в ту же сторону. Это означает, что такой участок обязательно будет потребителем энергии, полученной из остальной цепи. Кроме того, под действием сторонних сил он получает дополнительную энергию. Итак, единичный заряд, получив энергию от остальной цепи, на таком участке цепи получает еще энергию и всю эту энергию расходует на тепловое действие, которое оценивает падением напряжения . Таким образом,

Определив I, получим закон Ома для такого участка цепи:

Объединяя все три случая, можно следующим образом сформулировать закон Ома для участка цепи с э. д. c.: сила тока на участке цепи с э. д. с. прямо пропорциональна алгебраической сумме напряжения и э. д. с. на атом участке и обратно пропорциональна его сопротивлению.

При расчетах, когда знак или не известен, следует пользоваться формулой (16.39). Если в результате решения найденная величина или окажется отрицательной, то это будет означать, что ее действие на заряды в действительности обратно принятому при решении.

Заметим, что для неразветвлённой цепи с несколькими источниками э. д. с. закон Ома для всей цепи имеет вид

где т — число э. д. с., а п — число сопротивлений во всей цепи. Здесь в числителе — алгебраическая сумма всех э. д. с., причем э. д. с. на участке цепи положительна, если по направлению тока потенциал на этом участке возрастает; если же потенциал в этом направлении убывает, то значение э. д. с. берется с минусом.

Для схемы рис. 16.16 формула (16.40) имеет вид

Услуги по физике:

Лекции по физике:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник