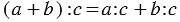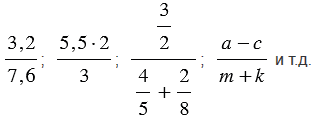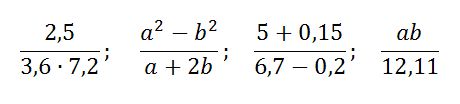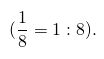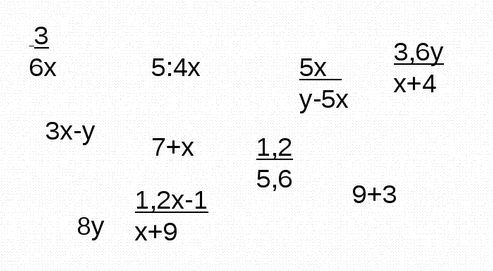Что называется дробным выражением
Деление и дроби
Не всегда можно одно натуральное число разделить на другое, так, например, 2 нельзя разделить на 3, в таком случае деление можно заменить дробью 

Пример:
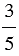
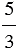
| В результате деления двух натуральных чисел может получится натуральное число или дробное число. |
Пример:
20 : 4 = 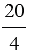
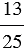
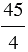
| Всякое натуральное число может быть записано в виде дроби, причем натуральное число можно представить в виде дроби с каким угодно знаменателем. |
Пример:
Получаем, что число 1 можно представить в виде дроби, у которой числитель и знаменатель равны.
Свойство деления суммы на число
Чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные частные.
Пример:
(64 + 72) : 8 = 64 : 8 + 72 : 8 = 8 + 9 = 17.
Дробные выражения
| Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением. |
К дробным выражениям относятся:
Обратите внимание, в числителе и в знаменателе дробного выражения могут стоять любые числа (натуральные числа, обыкновенные дроби, десятичные дроби и т.д.), а также числовые или буквенные выражения (смотри примеры выше).
Если числитель и знаменатель дробного выражения разделить или умножить на одно и то же число отличное от нуля, то получим дробное выражение, равное данному. Данное свойство часто используют, когда преобразуют дробное выражение с десятичными дробями в обыкновенную дробь.
Пример:
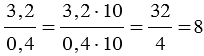
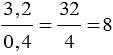
То есть, получается, что мы переносим запятую в числителе и знаменателе дробного выражения на одинаковое количество цифр вправо, при этом если в одном числе цифр после запятой больше, чем в другом, то переносим запятую на большее количество цифр, а там где цифр после запятой меньше дописываем нули.
Пример:
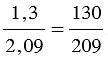
Поделись с друзьями в социальных сетях:
Что называется дробным выражением
В курсе алгебры 7 класса мы занимались преобразованиями целых выражений, т. е. выражений, составленных из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число, отличное от нуля. Так, целыми являются выражения
В отличие от них выражения
помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными. Такие выражения называют дробными выражениями.
Целые и дробные выражения называют рациональными выражениями.
Целое выражение имеет смысл при любых значениях входящих в него переменных, так как для нахождения значения целого выражения нужно выполнить действия, которые всегда возможны.
Дробное выражение при некоторых значениях переменных может не иметь смысла. Например, выражение не имеет смысла
при а = 0. При всех остальных значениях а это выражение имеет
смысл. Выражение имеет смысл при тех значениях х и у, x ≠ y.
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.
Выражение вида называется, как известно, дробью.
Дробь, числитель и знаменатель которой многочлены, называют рациональной дробью.
Примерами рациональных дробей служат дроби
В рациональной дроби допустимыми являются те значения переменных, при которых не обращается в нуль знаменатель дроби.
Пример 1. Найдем допустимые значения переменной в дроби
Это уравнение имеет два корня: 0 и 9. Следовательно, допустимыми значениями переменной а являются все числа, кроме 0 и 9.
Дробь равна нулю тогда и только тогда, когда a = 0 и b ≠ 0.
2. Основное свойство дроби. Сокращение дробей
Мы знаем, что для обыкновенных дробей выполняется следующее свойство: если числитель и знаменатель дроби умножить на одно и то же натуральное число, то значение дроби не изменится. Иначе говоря, при любых натуральных значениях а, b и с верно paвенство
Докажем, что это равенство верно не только при натуральных, но и при любых других значениях а, b и с, при которых знаменатель отличен от нуля, т. е. при b ≠ О и с ≠ О.
Пусть Тогда по определению частного а = bm. Умножим обе части этого равенства на с :
На основании сочетательного и переместительного свойств умножения имеем:
Так как bс ≠ 0, то по определению частного
Мы показали, что для любых числовых значений переменных b и с, где b ≠ О и с ≠ 0, верно равенство
Равенство (1) сохраняет силу и в том случае, когда под буквами а, b и с понимают многочлены, причем b и с — ненулевые многочлены, т. е. многочлены, не равные тождественно нулю.
Равенство (1) выражает основное свойство рациональной дроби:
если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.
Это равенство верно при всех допустимых значениях переменных. Такие равенства будем называть тождествами. Ранее тождествами мы называли равенства, верные при всех значениях переменных. Теперь мы расширяем понятие тождества.
Определение. Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.
Основное свойство рациональной дроби позволяет выполнять приведение дроби к новому знаменателю и сокращение дробей. Приведем примеры.
Пример 1. Приведем дробь к знаменателю
Множитель называют дополнительным множителем к числителю и знаменателю дроби
Пример 2. Приведем дробь к знаменателю
Для этого числитель и знаменатель данной дроби умножим на -1:
если изменить знак числителя (или знак знаменателя) дроби и знак перед дробью, то получим выражение, тождественно равное данному.
Пример 3. Сократим дробь
Разложим числитель и знаменатель дроби на множители:
Сократим полученную дробь на общий множитель a + 3:
Пример 4. Построим график функции
Графиком функции является прямая, а графиком функции но с «выколотой» точкой (4 ; 4) (рис. 1.)
Урок 20 Бесплатно Дробные выражения
В этом уроке мы познакомимся с понятием дробных выражений и с тем, как их считать. Узнаем интересные способы работы с дробями, в числителе или знаменателе которых стоят дроби.
Дробные выражения
Для начала определимся с определением дробного выражения.
Дробным выражением называется частное двух выражений или чисел, знак деления в котором обозначается чертой.
Пример:
Мы привыкли называть такое выражение обыкновенной дробью. Она ничем не противоречит определению дробного выражения. Поэтому если вас спросят: «Является ли обыкновенная дробь дробным выражением?», то можно смело ответить: «Да, является!»
Мы не накладываем никаких ограничений на то, что из себя представляют выражения; нужно только то, чтобы это было деление, записанное как дробь.
Также никто не запрещает записать в одну или даже в обе части выражения, содержащие дроби.
Примеры:
Можем пойти дальше и записать так называемую многоэтажную дробь. Это дробь, в числителе или в знаменателе (а иногда и в числителе и в знаменателе) которой стоят дробные выражения.
Примеры:
Помимо определения дробного выражения необходимо знать определения числителя и знаменателя дробного выражения.
Если мы считаем дробное выражение делением, то числителем будет являться делимое, а знаменателем делитель.
Например, существует следующее дробное выражение:
В данном случае \(\mathbf<3+10\cdot2>\) будет являться числителем, а \(\mathbf<2+\frac<1><2>>\)- знаменателем.
Также можно преобразовывать обычные выражения в дробные.
Это можно делать при условии, что выражение представляет из себя частное двух выражений или чисел, но пока что записанное через обычный знак деления.
Примеры преобразования обычного выражения в дробное:
Сформулируем правило: для того, чтобы преобразовать выражение, представляющее из себя частное двух выражений или чисел, необходимо делимое поместить в числитель дробного выражения, а делитель- в знаменатель.
Теперь вы видите, насколько большой класс формул покрывается понятием дробного выражения.
Давайте пройдем небольшой тест и перейдем к изучению того, как вычислять значения дробных выражений.
Пройти тест и получить оценку можно после входа или регистрации
Вычисление дробных выражений
Начнем с самого простого способа вычисления значений дробных выражений.
Он заключается в том, чтобы отдельно посчитать значения числителя и знаменателя и получить дробное выражение, в знаменателе и числителе которого стоят числа.
Далее надо смотреть, что получилось:
Пример 1
Вычислим значение выражения \(\mathbf<\frac<1+2\cdot4><5-2>>\)
Решение:
Для начала вычислим значения числителя и знаменателя:
В данном примере числитель делится на знаменатель, поэтому из дроби получится натуральное число.
Пример 2
Решение:
Сначала вычислим числитель и знаменатель:
В данном случае получилась неправильная дробь, выделим целую ее часть, чтобы получить в ответе смешанное число:
Пока что были рассмотрены случаи, в которых выражения в числителе и знаменателе представляли из себя арифметические действия над натуральными числами. Но вас нисколько не должны смущать случаи, в которых выражения содержат в себе дроби как обыкновенные, так и десятичные.
Пример:
Решение:
Наверное, вы уже догадываетесь, что мы сделаем дальше. Правильно! Вычислим числитель и знаменатель:
В данном случае мы получили неправильную дробь в числителе и десятичную дробь в знаменателе.
Чтобы получить окончательный результат разделим одно на другое:
Прежде чем перейти к дополнительным приемам работы с дробными выражениями, решим небольшой тест для закрепления навыка вычисления дробных выражений.
Пройти тест и получить оценку можно после входа или регистрации
Приемы для работы с дробными выражениями
Пока что во всех предыдущих случаях мы находили значения дробных выражений «в лоб», по достаточно простому алгоритму.
Но, как это часто бывает в математике, в некоторых случаях можно упростить себе подсчеты, вовремя заметив определенные вещи.
Вы уже наверняка хорошо освоили сокращение дробей.
Напомним, в чем его суть: если числитель представляет из себя произведение, и знаменатель также является произведением, и в этих произведениях есть одинаковый множитель, то мы можем сократить дробь на этот множитель.
Как же это относится к дробным выражениям?
Дело в том, что в некоторых случаях числитель и знаменатель могут быть произведениями или же могут стать произведениями в процессе подсчетов.
Тогда почему бы не сокращать их по возможности?!
Пример:
Начнем считать выражение и посмотрим, что получается.
Числитель и знаменатель дробного выражения после первых преобразований превратились в произведения.
Также можно заметить, что в этих произведениях есть общий множитель: 127
Тогда мы можем поделить числитель и знаменатель дробного выражения на это число, тем самым значительно упростив выражение.
Это и будет значением этого выражения.
Также мы можем быть еще более хитрыми и внимательными.
Конечно же, можно начать вычислять сначала числитель, потом знаменатель. Для этого мы будем вычислять разность шестизначных чисел.
Но можно сделать проще: заметим, что числитель и знаменатель являются произведениями.
Числитель является произведением 2-х и выражения (478569-145236)
Знаменатель же является произведением выражения (478569-145236) и 3-х.
Выражение (478569-145236) является множителем и можно утверждать, что это один и тот же множитель в числителе и в знаменателе.
Значит, мы можем уверенно сокращать дробное выражение на это выражение.
В данном случае мы сразу получили правильную дробь, это и будет являться значением выражения.
Отдельно стоит упомянуть работу с многоэтажными дробями.
Но также можно запомнить два правила, которые существенно экономят время.
Первое правило говорит о том, что, если в числителе дробного выражения находится дробь (или же дробное выражение), мы можем домножить дробное выражение на знаменатель дроби (или дробного выражения), стоящей в числителе, тем самым уменьшив «этажность» дробного выражения.
Второе правило рассматривает случай, когда дробь (или дробное выражение) находится в знаменателе дробного выражения.
В таком случае уменьшить «этажность» дробного выражения поможет домножение всего дробного выражения на знаменатель дроби (или дробного выражения), стоящей в знаменателе.
И парочка примеров на этот случай:
И в завершение еще дам такой пример:
Пройти тест и получить оценку можно после входа или регистрации
Интересная информация
Десять интересных математических фактов:
1. Известные всем знаки сложения и вычитания впервые были использованы только около 500 лет назад
2. 2 и 5— единственные простые числа, которые оканчиваются на 2 или 5
3. Несмотря на то, что сохранилось много трудов древнегреческого ученого Евклида, о его биографии почти ничего не известно
4. В римской системе счисления не существует нуля
5. Знак равенства «=» появился только в XVI веке
6. Слово «миг» обозначает не только короткое мгновение, но и вполне конкретный временной промежуток: 0,01 секунды
7. У древних египтян отсутствовала таблицы умножения и прочие математические правила
8. В свое время заниматься математикой в высоких кругах было настолько популярно, что даже Наполеон Бонапарт оставил после себя научные труды
9. Самые древние математические записи были найдены написанными на костях
10. Ученый Муавр с помощью математики смог рассчитать дату своей смерти
Заключительный тест
Пройти тест и получить оценку можно после входа или регистрации
Что называется дробным выражением
Алгебраическое выражение в записи которого наряду с действиями сложения, вычитания и умножения используют также деление на буквенные выражения, называется дробным алгебраическим выражением. Таковы, например, выражения
Алгебраической дробью мы называем алгебраическое выражение, имеющее вид частного от деления двух целых алгебраических выражений (например, одночленов или многочленов). Таковы, например, выражения


Тождественные преобразования дробных алгебраических выражений имеют по большей части своей целью представить их в виде алгебраической дроби. Для отыскания общего знаменателя используется разложение на множители знаменателей дробей — слагаемых с целью отыскания их наименьшего общего кратного. При сокращении алгебраических дробей может нарушаться строгая тождественность выражений: необходимо исключать значения величин, при которых множитель, на который производится сокращение, обращается в нуль.
Приведем примеры тождественных преобразований дробных алгебраических выражений.
Пример 1. Упростить выражение
Все слагаемые можно привести к общему знаменателю 
Наше выражение равно единице при всех значениях 


Пример 2. Представить в виде алгебраической дроби выражение
Решение. За общий знаменатель можно принять выражение 
1. Найти значения алгебраических выражений при указанных значениях параметров:
2. Разложить на множители:
3. Раскрыть скобки в выражении 
4. Найти разложение степени бинома
5. Вычислить, пользуясь формулой бинома Ньютона, степени комплексных чисел: а) 

В разложении 


7. Упростить следующие рациональные алгебраические выражения:
Что называется дробным выражением
Сегодня на уроке мы с вами приступим к изучению дробных выражений. Для начала начнем с определения, и узнаем, какие именно выражения принято называть дробными.
Дробные выражения – это частное 2-х чисел или выражений, знак деления которого обозначают чертой.
В дробном выражении, то выражение, которое стоит под этой дробной чертой, называют знаменателем.
В дробном выражении его числителями и знаменателями являются какие-либо числа или буквенные выражения.
Вот несколько примеров дробных выражений:
Также как и с обыкновенными дробями, так и с дробными выражениями все действия делаются по одним и тем же правила.
Что такое простая дробь
Прежде чем приступить к изучению дробных выражений и выполнению практических заданий, давайте вспомним, что такое дроби.
Простой дробью называют часть единицы или ее нескольких частей.
Знаменателем простой дроби называют то количество равных частей, на которое делится единица. А числителем простой дроби называют количество взятых частей.
Простая дробь записывается в таком виде:
Из этого следует, что дробь — это число, составленное из целого числа долей единицы.
Историческая справка о математических дробях
А теперь давайте заглянем в историю и попробуем узнать, когда люди познакомились с понятием дробь. Естественно, что это понятие возникло не сразу, вначале у человека сформировалось представление о целых числах, а потом люди пришли к пониманию «половины».
Вначале древний человек научился считать предметы, но позднее пришло понимание для измерения длины, времени, площади и вести расчеты при купле-продаже. А в этих случаях не всегда удавалось использовать только натуральные числа, а необходимо было учитывать и какие-то части или доли. Вот так постепенно и появились дроби.
Исторический след исчисления дробей был замечен в использовании многих народов. В Древнем Вавилоне существовала мера в один талант, что составляло 60 мин, одна мина равнялась 60 шекелей. То есть, можно сказать, что в вавилонской системе исчислений применялись шестидесятеричные дроби.
Древние римляне пользовались двенадцатеричными дробями, поскольку у них в весовой системе один «асе» делился на 12 унций. Так, дробь, которую мы знаем, как 1/12 римляне называли «унцией», а «1/8» получила название «полторы унции».
Индийцам также были известны обыкновенные дроби, но они слегка отличались от наших дробей, так как у индусов отсутствовала дробная черта. У греков была своя запись дробей. Они знаменатель писали сверху, а числитель – снизу. Также часто использовали и такую запись, как 3 5х – это значило три пятых. А вот в русском языке термин «дробь» происходило от глагола «дробить», ломать, делить на части и получил широкое применение только в VIII веке. В первых учебниках по математике вместо дробей использовалось название «ломаные числа».
Домашнее задание
Дайте ответы на следующие вопросы:
1. Назовите действия, которые необходимые выполнить, чтобы найти дробь от числа?
2. Какие вы знаете способы нахождения числа по его значению дроби?
3. Сформулируйте правило умножения обыкновенных дробей.
4. Сформулируйте правило деления обыкновенных дробей.
5. Какие выражения принято называть дробными?
6. Чем дробные выражения отличаются от остальных?
Перед вами предоставлены различные виды выражений, выберите из них те, которые являются дробными выражениями.
1. Таня читает интересную книгу и уже прочла 32 страницы, это составляет 2/3 всей книги. Дайте ответ, сколько в этой книге страниц?
2. Денису четырнадцать лет. Его возраст составляет 2/7 возраста отца. Решите задачу и ответьте, сколько же лет отцу Дениса?