Что называется дизъюнкцией двух высказываний
Лекция 8. Конъюнкция и дизъюнкция высказываний.
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Лекция 8. Конъюнкция и дизъюнкция высказываний.
КОНЪЮНКЦИЕЙ (или логическим произведением) двух высказываний называется высказывание «А и В», которое истинно тогда и только тогда, когда оба высказывания истинны ( А истинно и В истинно). Во всех остальных случаях высказывание «А и В» ложно.
Для задания таких связок удобно записывать таблицы истинности:
Согласно определению, конъюнкция двух элементарных высказываний истинна только в том случае, когда истинны оба высказывания, ее образующие (строка 1), и ложна в любом другом случае (строка2,3,4).
КОНЪЮНКЦИЯ А = истинна только тогда, когда Петя любит физику, а математику не любит. В остальных трех случаях, т.е. когда Петя:
не любит математику и не любит физику,
любит математику и физику,
любит математику, но не любит физику
высказывание А В ложно.
Достаточно часто для выражения конъюнкции вместо союза «и» используются союзы «а», «но», «хотя», «однако» и др. Но союз «и» не всегда обозначает конъюнктивную связь предложений. Рассмотрим два высказывания: «7и13 – взаимно простые числа». Здесь первое предложение – сокращенная запись конъюнкции «7 – простое число и 13 – простое число». Второе предложение – элементарное, которое выражает отношение между двумя числами 7 и 13, состоящее в том, что у них нет общего делителя, отличного от единицы. Значит, во втором предложении союз «и» связывает не два суждения, а два предмета, которые находятся в определенном соотношении. Логический союз «и» отличается от грамматического союза «и» еще и тем, что грамматическим союзом «и» соединяют суждения, имеющие между собой что-нибудь общее по содержанию, а логический союз «и» может соединять любые суждения. Например, суждение «Т.Г. Шевченко – поэт и число 3201 делится на 3» в логике являются истинными, так как единственным условием для того, чтобы конъюнктивное суждение было истинным, является истинность его составных суждений.
Таблица истинности для дизъюнкции имеет вид:
Дизъюнкция А VВ = будет истинной, если на первом уроке будет литература (вторая строка таблицы истинности) или математика (третья строка таблицы истинности), и ложной, если на первом уроке будет любой другой предмет или если урока вообще не будет (четвертая строка таблицы истинности).
Согласно Единой спортивной квалификации и высказывание А, и высказывание В истинны, следовательно, и дизъюнкция их истинна (1-я строка таблицы истинности).
Как видно из приведенных примеров, для образования дизъюнкции используется союз «или». В обычной речи этот союз чаще всего имеет разделительный смысл (как в примере 1: либо математика, либо литература), но не всегда. В примере 2 союз «или» лишен разделительного оттенка: шахматист одновременно может набрать 11,5 очка и занять 1-е место.
В математике союз «или» всегда понимается в широком смысле.
Задания для самостоятельной работы по теме:
Определите значение истинности следующих высказываний:
а) «Париж расположен на Сене и 2+3=4»;
б) «Число 4 – простое и это число четное»;
в) «Днепропетровск – столица Украины и Миссисипи протекает в Австралии»;
2. Составьте 2-4 сложных высказывания на конъюнкцию, определите их истинность.
3. Определите значение истинности высказываний А,В, если:
4. Сформулируйте и запишите в виде конъюнкции условие истинности каждого предложения
(а, в ϵ R ): а) а×в≠0; б) а÷в=0; в) а 2 + в 2 = 0;
Определите значение истинности следующих высказываний:
а) «Число 4 простое или это число четное»;
б) «2 + 2 = 4 или белые медведи живут в Африке»;
в) «2 + 2 = 5 или Днепр впадает в белое море»;
г) «2 + 2 = 4 или Днепр впадает в Черное море».
5. Составьте 2-4 сложных высказывания на дизъюнкцию, определите их истинность.
6. Определите значение истинности высказываний С и D, если:
7. Сформулируйте и запишите в виде дизъюнкции условие истинности каждого предложения (а, в ϵ R ):а) а × в = 0, б) >2.
Что называется дизъюнкцией двух высказываний

2. Построение таблиц истинности и логических функций.
3. Законы логики и преобразование логических выражений.
Лабораторная работа № 3. Основы математической логики.

Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики). Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).
Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно.
Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.
Высказывания 1 и 3 являются истинными. Высказывание 2 – ложным , потому что число 27 составное 27=3*3*3.
Итак, отличительным признаком высказывания является свойство быть истинным или ложным, последние четыре предложения этим свойством не обладают.
С помощью высказываний устанавливаются свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно.
Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание «Число 1 +22 = 4294 967297 — простое», принадлежащее Ферма (1601-1665), долгое время считалось истинным, пока в 1732 году Эйлер (1707-1783) не доказал, что оно ложно. В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна 180°» устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.
В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные, большими буквами латинского алфавита.
Существуют разные варианты обозначения истинности и ложности логических переменных:
Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух) связанных логическими операциями.
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).
Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.
Введем перечисленные логические операции.
В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
Конъюнкция и дизъюнкция высказываний



Рассмотрим составное высказывание, которое образуется из элементарных высказываний с помощью союза «и».
Союз «и» в русском языке имеет различные смысловые оттенки. Например, предложение «Кубик маленький и красный» будет истинным, если истинны оба составляющих предложения. А предложение «На этих местах сидят дети и инвалиды» истинно, если истинно хотя бы одно из составляющих предложений. В математической речи союз «и» употребляется только в первом смысле.
Пусть даны высказывания А и В.
Конъюнкцией высказываний А и В называется высказывание, которое истинно, когда истинны оба данные высказывания одновременно.
Конъюнкция высказываний А и В обозначается: АÙВ. Читаем: «Конъюнкция высказываний А и В» или «А и В».
Название «конъюнкция» произошло от латинского слова «conjunctio», что означает «союз, связь или единение». Определение конъюнкции высказываний А и В можно записать в следующей таблице.
| А | В | АÙВ |
| и | и | и |
| и | л | л |
| л | и | л |
| л | л | л |
Замечание. В этой таблице, кроме первой строки для обозначения высказываний, еще – 4 строки для комбинаций значений истинности высказываний А и В. Для подсчета числа комбинаций используется комбинаторная задача – размещение с повторениями, т.к. мы два значения истинности («и» или «л») распределяем на два высказывания.
Используя формулу для подсчета числа размещений с повторениями Ā 
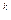
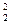
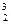
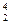
1. Составное высказывание «Число 2 чётное и простое» будет истинным, т.к. оно является конъюнкцией двух истинных высказываний «Число 2 чётное» и «Число 2 простое».
2. Составное высказывание «Число 14 четное и простое» будет ложным, т.к. оно представляет собой конъюнкцию двух высказываний «Число 14 четное» и «Число 14 простое», из которых первое истинно, а второе ложно.
3. Составное высказывание «8
Например, «Число 16 делится не только на 2, но и на 4».
Рассмотрим составное высказывание, которое образуется из элементарных высказываний с помощью союза «или».
Предложение «Идет дождь или светит солнце» будет истинным, если истинно хотя бы одно из составляющих предложений, причем не исключается возможность истинности обоих предложений. Именно в этом смысле понимается союз «или» и в математическом языке.
Пусть даны высказывания А и В.
Дизъюнкцией высказываний А и В называется высказывание, которое истинно, когда истинно хотя бы одно из данных высказываний.
Дизъюнкция высказываний А и В обозначается: А 
Название «дизъюнкция» произошло от латинского слова «disjunctio», что означает «разделение, разобщение».
Определение дизъюнкции высказываний А и В можно записать в следующей таблице.
| А | В | А  В В |
| и | и | и |
| и | л | и |
| л | и | и |
| л | л | л |
1. Составное высказывание «Число 14 чётное или простое» будет истинным, т.к. оно представляет собой дизъюнкцию высказываний «Число 14 чётное» и «Число 14 простое», где первое – истинно, а второе – ложно.
2. Составное высказывание «Число 36 делится на 6 или на 9» будет также истинным, т.к. оно является дизъюнкцией двух истинных высказываний «Число 36 делится на 6» и «Число 36 делится на 9».
3. Составное высказывание «4≥6» будет ложным, т.к. оно представляет собой дизъюнкцию двух ложных высказываний «4>6» и «4=6».
4. Пример использования составного высказывания «А или В» в работе с детьми дошкольного возраста. Наглядный материал изображён на рисунке 17:
Задание ребенку: «Возьми фигуру, похожую на яблоко по цвету или по форме».





Элементарные предложения: А – «форма как у яблока», В – «цвет как у яблока».
| Выбор ребенка | Значение истинности элементарных предложений | Оценка воспитателя | |
| А | В | ||
 | и | и | «правильно» |
 | и | л | «правильно» |
 | л | и | «правильно» |
 | л | л | «неправильно» |
Замечание. Определения конъюнкции и дизъюнкции двух высказываний можно обобщить на n составляющих их высказываний.
Конъюнкцией высказываний A 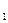
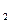

Дизъюнкцией высказываний A 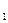
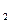

Для операций конъюнкции и дизъюнкции высказываний выполняются одинаковые законы, поэтому рациональнее рассматривать их одновременно.
I. Закон коммутативности
а) конъюнкции высказываний: ( 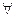


б) дизъюнкции высказываний: ( 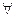


I а) читаем: «Для любых высказываний А и В конъюнкция высказываний А и В равносильна конъюнкции высказываний В и А».
I б) читаем: «Для любых высказываний А и В дизъюнкция высказываний А и В равносильна дизъюнкции высказываний В и А».
Название этого закона произошло от латинского слова «commutatio», что означает «перемена», поэтому закон иначе называется переместительным (от перемены мест высказываний конъюнкция или дизъюнкция не меняется).
Доказательство законов Iа и Iб проводят в таблицах истинности.
| А | В | A B B | B A A | А | В | A B B | B A A |
| и | и | и | и | и | и | и | и |
| и | л | л | л | и | л | и | и |
| л | и | л | л | л | и | и | и |
| л | л | л | л | л | л | л | л |
Сравнивая в этих таблицах значения истинности для результатов операций A











II. Закон ассоциативности
а) конъюнкции высказываний: ( 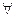




б) дизъюнкции высказываний: ( 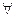




II а) читаем: «Для любых высказываний А, В и С конъюнкция высказывания А с конъюнкцией высказываний В и С равносильна конъюнкции высказывания С с конъюнкцией высказываний А и В».
II б) читаем: «Для любых высказываний А, В и С дизъюнкция высказывания А с дизъюнкцией высказываний В и С равносильна дизъюнкции высказывания С с дизъюнкцией высказываний А и В».
Название закона произошло от латинского слова «associatio», что означает «сочетание, соединение», поэтому он иначе называется сочетательным (от перемены мест скобок конъюнкция или дизъюнкция не меняется).
В следующей таблице истинности докажем закон II а.
| А | В | С | B C C | A (B (B C) C) | A B B | (A B) B) C C |
| и | и | и | и | и | и | и |
| и | и | л | л | л | и | л |
| и | л | и | л | л | л | л |
| и | л | л | л | л | л | л |
| л | и | и | и | л | л | л |
| л | л | и | л | л | л | л |
| л | л | л | л | л | л | л |
Сравнивая в этой таблице по строкам значения истинности для результатов операций A







Закон II б предлагается доказать самостоятельно.
III. Закон дистрибутивности
а) конъюнкции относительно дизъюнкции: ( 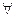





б) дизъюнкции относительно конъюнкции: ( 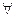





Название закона произошло от латинского слова «distributio», что означает «распределение», поэтому иначе его называют распределительным законом.
III а) читаем: «Для любых высказываний А, В и С конъюнкция высказывания А с дизъюнкцией высказываний В и С равносильна дизъюнкции конъюнкции А и В с конъюнкцией высказываний А и С».
III б) читаем: «Для любых высказываний А, В и С дизъюнкция высказывания А с конъюнкцией высказываний В и С равносильна конъюнкции дизъюнкции А и В с дизъюнкцией А и С».
Докажем закон IIIа дистрибутивности конъюнкции относительно дизъюнкции, используя таблицу истинности и определения операций конъюнкции и дизъюнкции.
| А | В | С | B C C | A (B (B C) C) | A B B | A С С | (A B) B) (А (А C) C) |
| и | и | и | и | и | и | и | и |
| и | и | л | и | и | и | л | и |
| и | л | и | и | и | л | и | и |
| и | л | л | л | л | л | л | л |
| л | и | и | и | л | л | л | л |
| л | и | л | и | л | л | л | л |
| л | л | и | и | л | л | л | л |
| л | л | л | л | л | л | л | л |
Сравнивая по строкам значения истинности для результатов операций A














Закон III б предлагается доказать самостоятельно.
IV. Законы де Моргана
а) отрицание конъюнкции: ( 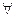


б) отрицание дизъюнкции: ( 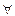
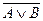

IV а) читаем: «Для любых высказываний А и В отрицание конъюнкции высказываний А и В равносильно дизъюнкции отрицаний высказываний А и В».
IV б) читаем: «Для любых высказываний А и В отрицание дизъюнкции высказываний А и В равносильно конъюнкции отрицаний высказываний А и В».
Доказательство этих законов выполнено в следующих таблицах.
| А | В | A B B |  | Ā | `В | `А  `B `B | А | В | A B B | 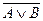 | Ā | `В | `А  `B `B |
| и | и | и | л | л | л | л | и | и | и | л | л | л | л |
| и | л | л | и | л | и | и | и | л | и | л | л | и | л |
| л | и | л | и | и | л | и | л | и | и | л | и | л | л |
| л | л | л | и | и | и | и | л | л | л | и | и | и | и |
Сравнивая по строкам значения истинности для результатов операций 

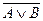

Рассмотрим применение этих законов на следующих примерах.





