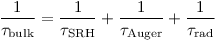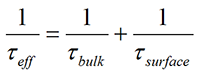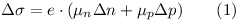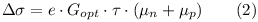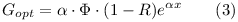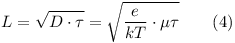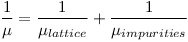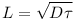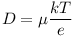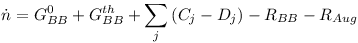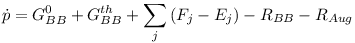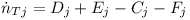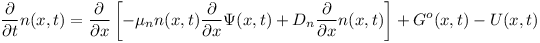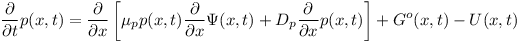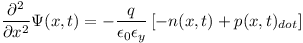Что называется диффузионной длиной

диффузионная длина

Смотреть что такое «диффузионная длина» в других словарях:

диффузионная длина — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN diffusion length … Справочник технического переводчика

диффузионная длина — difuzijos nuotolis statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. diffusion length vok. Diffusionslänge, f rus. диффузионная длина, f; длина диффузии, f pranc.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

диффузионная длина — difuzijos nuotolis statusas T sritis Standartizacija ir metrologija apibrėžtis Kvadratinė šaknis iš difuzijos ploto. atitikmenys: angl. diffusion length vok. Diffusionslänge, f rus. диффузионная длина, f; длина диффузии, f pranc. distance de… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

диффузионная длина неосновных носителей заряда полупроводника — диффузионная длина Расстояние, на котором в однородном полупроводнике при одномерной диффузии в отсутствие электрического и магнитного полей избыточная концентрация неосновных носителей заряда уменьшается вследствие рекомбинации в е раз. [ГОСТ… … Справочник технического переводчика

диффузионная длина пламени — (в топке котла) [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN diffusion distance … Справочник технического переводчика

Диффузионная длина неосновных носителей заряда полупроводника — 33. Диффузионная длина неосновных носителей заряда полупроводника Диффузионная длина Расстояние, на котором в однородном полупроводнике при одномерной диффузии в отсутствие электрического и магнитного полей избыточная концентрация неосновных… … Словарь-справочник терминов нормативно-технической документации

диффузионная длина электронов — elektronų difuzijos nuotolis statusas T sritis radioelektronika atitikmenys: angl. electron diffusion length vok. Elektronendiffusionslänge, f rus. диффузионная длина электронов, f pranc. longueur de diffusion d électrons, f … Radioelektronikos terminų žodynas

диффузионная длина дырок — skylių difuzijos nuotolis statusas T sritis radioelektronika atitikmenys: angl. hole diffusion length vok. Löcherdiffusionslänge, f rus. диффузионная длина дырок, f pranc. distance de diffusion des trous, f; parcours de diffusion des trous, m … Radioelektronikos terminų žodynas

длина диффузии — difuzijos nuotolis statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. diffusion length vok. Diffusionslänge, f rus. диффузионная длина, f; длина диффузии, f pranc.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

длина диффузии — difuzijos nuotolis statusas T sritis Standartizacija ir metrologija apibrėžtis Kvadratinė šaknis iš difuzijos ploto. atitikmenys: angl. diffusion length vok. Diffusionslänge, f rus. диффузионная длина, f; длина диффузии, f pranc. distance de… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

Источник

Большая Энциклопедия Нефти и Газа

Диффузионная длина

Диффузионная длина не должна быть меньше чем 0 3 мм. Поэтому проводимость области между рассматриваемыми близко друг от друга эмиттерным и базовым контактами будет модулирована инжектированным током. [4]

Диффузионная длина определяет расстояние от границы стержня, на котором концентрация неравновесных носителей уменьшается в в раз по сравнению с ее граничным значением. Диффузионная длина неосновных носителей является важным электрофизическим параметром полупроводника. Она увеличивается с ростом времени жизни и коэффициента диффузии. [5]

Диффузионная длина L еще более чувствительна к искажениям кристаллической решетки, чем подвижность. [6]

Диффузионная длина носителей тока представляет собой среднюю величину, численное значение которой определяется диффузионными длинами всех электронов проводимости. Значение диффузионной длины играет важную роль в решении ряда практических задач полупроводниковой электроники. [7]

Диффузионной длиной L называют расстояние, на котором концентрация неравновесных носителей заряда убывает в е раз. [9]

Если диффузионная длина полупроводника сравнима с толщиной пластинки, то действительное сопротивление будет несколько меньше вследствие уменьшения р за счет инъекции носителей тока. [11]

Измерение диффузионной длины методом подвижного светового зонда дает возможность определить диффузионную длину и скорость поверхностной рекомбинации по результатам измерений фототока в двух точках образца. [12]

Измерения диффузионной длины и времени жизни носителей заряда, основанные на люминесценции, обязаны своим развитием использованию полупроводниковых соединений в светодиодах и лазерах. [14]

Понятие диффузионной длины играет важную роль в теории фотоэлектрических и контактных явлений. [15]

Источник

Электрические свойства полупроводников

Производительность полупроводниковых устройств в основном зависит от электрических параметров исходного материала, а также от наличия тех или иных электрических дефектов. С развитием усовершенствованного MDP метода анализа стало возможным измерение ключевых электрических свойств полупроводников с высокой чувствительностью, разрешением и скоростью.

Время жизни неосновных носителей заряда

Данный параметр является одним из наиболее важных и значимых параметров материала. Он чрезвычайно чувствителен к наименьшему количеству примесей или собственных дефектов материала и, следовательно, является идеальным параметром для онлайн анализа качества материала и технологического процесса. Время жизни неосновных носителей заряда имеет важное значение для производительности многих полупроводниковых приборов. Время жизни носителя определяется как среднее время, которое требуется избыточному неосновному носителю для рекомбинации, и также сильно зависит от величины и типа рекомбинационных процессов в полупроводнике.

Основными типами рекомбинационных процессов являются:

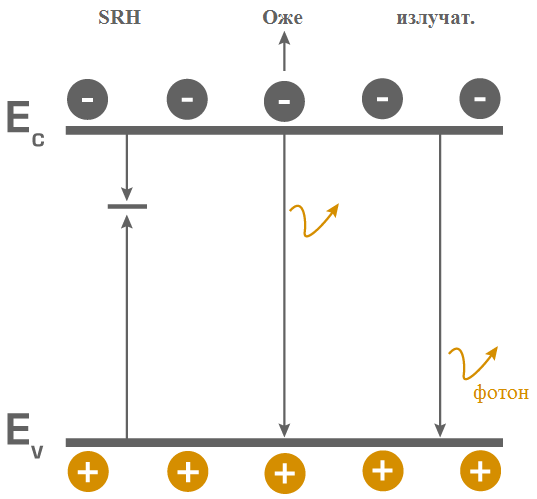
Для кремния SRH рекомбинация («Шокли-Рида-Холла») часто является доминирующим механизмом рекомбинации. Время жизни неосновных носителей заряда в объеме (τ_bulk) зависит соответственно от количества присутствующих дефектов и их рекомбинационных свойств. В кремнии время жизни может достигать 1 мс, тогда как в прямозонном полупроводнике, таком как GaAs, где доминирующей является излучательная рекомбинация, время жизни находится в диапазоне нс…мкс.

Рис. 1. Энергетическая схема различных типов рекомбинации.

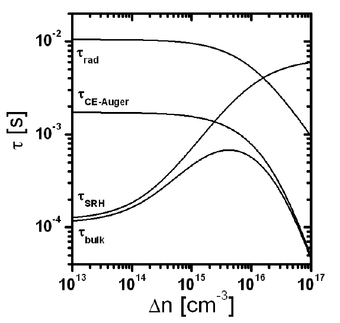
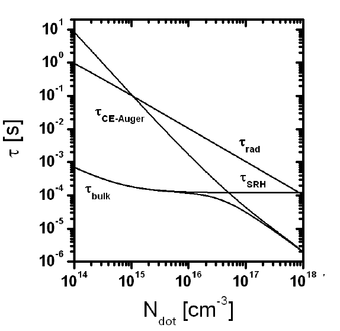
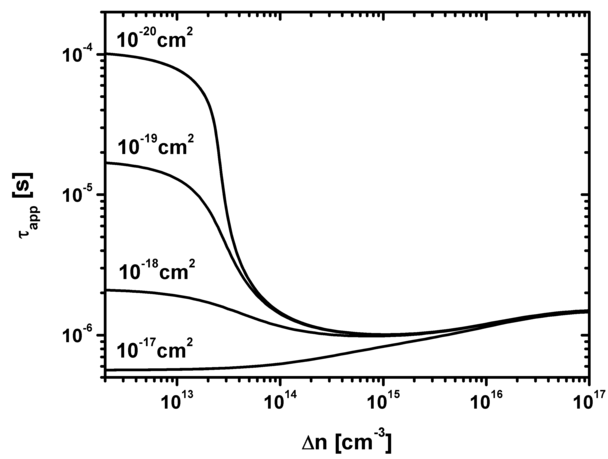
Помимо дефектов, время жизни неосновных носителей зависит от уровня инжекции (концентрации избыточных носителей) и концентрации легирующей примеси. На рисунках 2 и 3 отображены зависимости времени жизни от двух последних параметров.

Рис. 2. Зависимость типов рекомбинации от уровня инжекции.

Рис. 3. Зависимость типов рекомбинации от концентрации легирующей примеси.

Измеренное эффективное время жизни носителей (τ_eff) определяется объемным (τ_bulk) и поверхностным (τ_surface) временем жизни, зависящим от свойств поверхности материала, и может быть выражено через следующую формулу:

Следовательно, поверхность должна быть пассивирована, если требуется измерение объемных свойств по образцу. Если же необходимо исследовать качество пассивации поверхности, то рекомендуется проводить анализ, на примере кремния, на Fz-si, поскольку объемной рекомбинацией можно пренебречь. Также не стоит забывать, что измеренное эффективное время жизни носителей зависит от измерительного метода.

Фотопроводимость

Когда свет достаточной энергии поглощается полупроводником, число свободных электронов и дырок в нем изменяется и повышает его электропроводность. Это увеличение называется фотопроводностью, зависит от концентрации избыточных электронов и дырок и их подвижности и может быть выражено через следующие уравнения:

G_opt – это скорость оптической генерации, которая зависит от интенсивности падающего света, диаметра пятна на поверхности образца и длины волны излучения:

Из уравнения (2) следует, что фотопроводимость пропорционально произведению времени жизни τ и подвижности μ носителей заряда. Следовательно, она также пропорциональна квадрату диффузионной длины L, определяющейся по формуле (4):

Удельное сопротивление

Удельное электрическое сопротивление напрямую зависит от плотности полупроводника и, следовательно, является полезным параметром для контроля профиля распределения легирующей примеси и однородности. Время жизни и диффузионная длина также зависят от концентрации легирующей примеси. Поскольку легирование смещает уровень Ферми, то в большинстве случаев увеличивается скорость SRH рекомбинации. Кроме того, поскольку при сильном легировании более вероятна рекомбинация Оже, сам процесс рекомбинации также усиливается.

Часто удельное сопротивление измеряется бесконтактным методом вихревых токов. Вихревой ток возникает, когда образец подвергается воздействию изменяющегося магнитного поля из-за изменений поля во времени, например, если в катушке, расположенной в непосредственной близости от образца, протекает переменный ток. Это вызывает ток в объеме образца, а циркулирующие вихри тока создают индуцированные магнитные поля, которые противодействую изменению исходного магнитного поля. Чем выше электропроводность образца, тем больше развивающиеся токи и тем больше будет противоположное поле. Другими словами, измеряются электрические потери в материале, напрямую связанные с удельным сопротивлением образца.

Стоит также учитывать, что измерение зависит и от расстояния от катушки до образца и, следовательно, от геометрических особенностей образца.

Подвижность носителей заряда

Подвижность – это величина, связанная со скоростью дрейфа электронов или дырок в приложенном электрическом поле через материал. Подвижность зависит от различных процессов рассеяния, которые могут замедлять свободные носители, таких как столкновения с решеткой (lattice) или рассеяние на кристаллических дефектах и примесях (impurities) и определяется по следующей формуле:

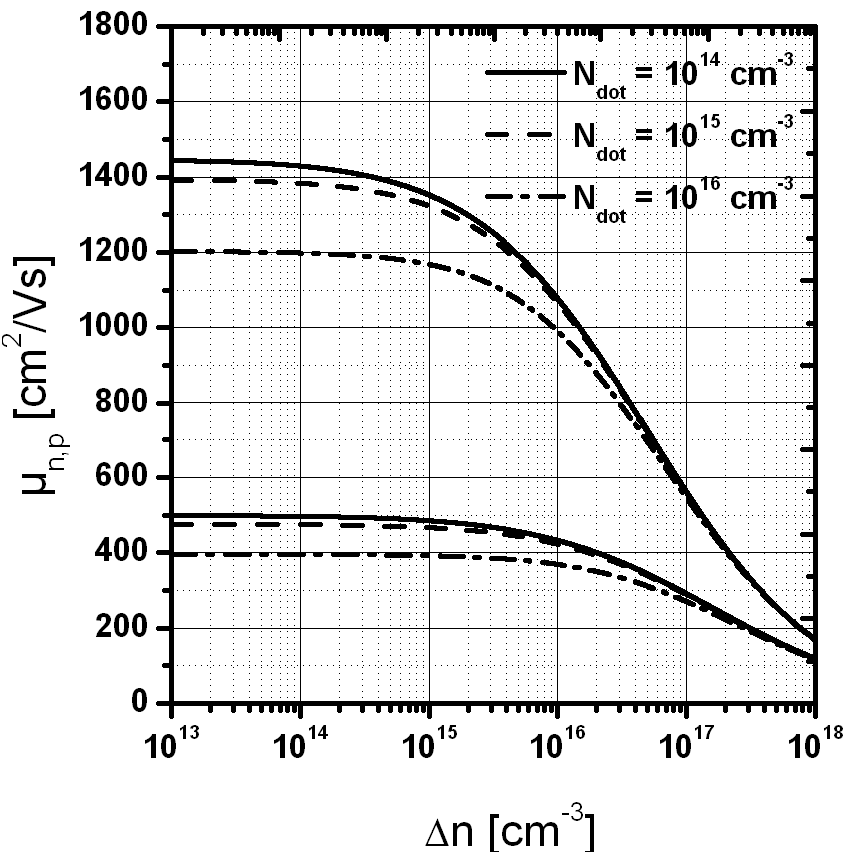
Следовательно, подвижность носителей заряда зависит от уровня легирования и плотности дефектов, а также от уровня инжекции. Обычно при моделировании и измерениях применяется модель Dorkel-Leturcq.

Рис. 4. Зависимость подвижности электронов и дырок от инжекции для разных концентраций легирующей примеси.

Диффузионная длина

Данный параметр представляет собой среднее расстояние, которое избыточные носители могут пройти, прежде чем они рекомбинируют. Диффузионная длина зависит от времени жизни носителей τ и их подвижности μ и определяется по следующей формуле:

где D – это диффузионный коэффициент, зависящий от подвижности носителей заряда:

Диффузионная длина служит своеобразным ограничением, влияющим на разрешающую способность для каждого электрического измерения. Например, при измерении образцов кремния высокого качества может быть достигнуто максимальное разрешение в 1 мм.

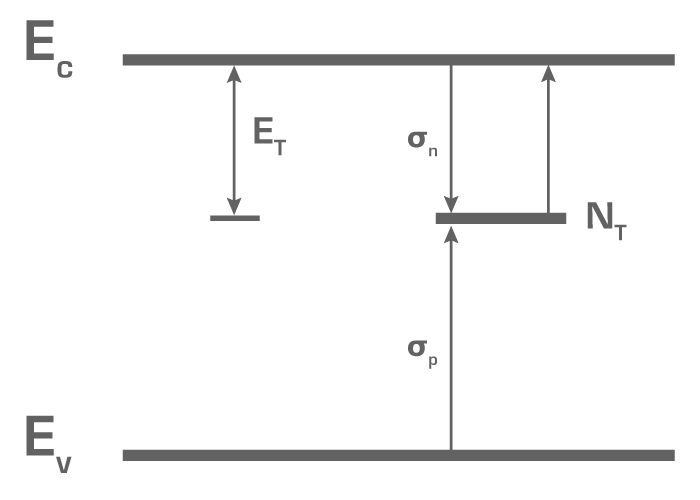
Свойства дефектов

Анализ данных свойств имеет особое значение для понимания эффективности и оценки качества материалов. Любой электрический дефект в полупроводнике определяется следующими параметрами:

Рис. 5. Энергетическая схема дефекта и его важных параметров.

Все эти свойства для оценки дефектов являются частью используемых имитационных моделей.

Имитационная модель времени жизни

Чтобы лучше понять измерения времени жизни и добиться более хорошей сопоставимости результатов между различными методами измерения, необходимо моделирование.

Обобщенные уравнения скорости для моделирования времени жизни

Данная модель основана на обобщенной системе уравнений скорости, которая решается для всех возможных переходов между уровнями дефектов в запрещенной зоне и зонами полупроводника. Единственное приближение состоит в том, что никакие взаимодействия между уровнями дефекта не включены в рассмотрение. Это является правильным приближением, так как плотность дефектов, например, в кремнии обычно низкая.

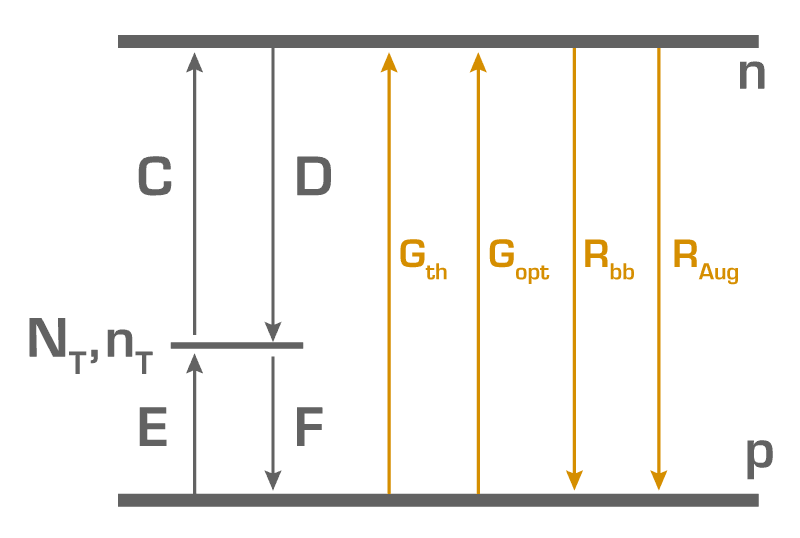
Применяемая система уравнений скорости описывает зависящее от времени изменение концентрации носителей в зоне проводимости и валентной зоне, а также на энергетических уровнях дефектов. В эту систему уравнений включены скорости оптической (G_opt) и тепловой (G_th) генерации, скорости межзонной рекомбинации (R_bb) и рекомбинации Оже (R_Aug), а также скорости захвата и излучения носителей от всех дефектов (C_j, D_j, E_j, F_j).

Рис. 6. Энергетическая схема всех скоростей перехода, которые учитываются при моделировании.

Скорости перехода без приближений могут быть описаны по следующим формулам:

Из смоделированной зависимости от времени изменения концентрации носителей с помощью модели подвижности Dorkel-Leturcq может быть рассчитана фотопроводимость. Далее время жизни неосновных носителей заряда может быть извлечено из переходного процесса фотопроводимости при принятии G_opt = 0.

Данная имитационная модель имеет ряд преимуществ по сравнению с SRH или PC1D:

Инструмент численного моделирования подходит для моделирования измерений, связанных с инжекцией и температурой, для исследования влияния захвата на время жизни и фотопроводимость, а также для сравнения MDP и µ-PCD или других методов измерений. Подводя итог можно сказать, что данный тип моделирования позволяет сделать измерения времени жизни более сопоставимыми и добиться лучшего понимания результатов.

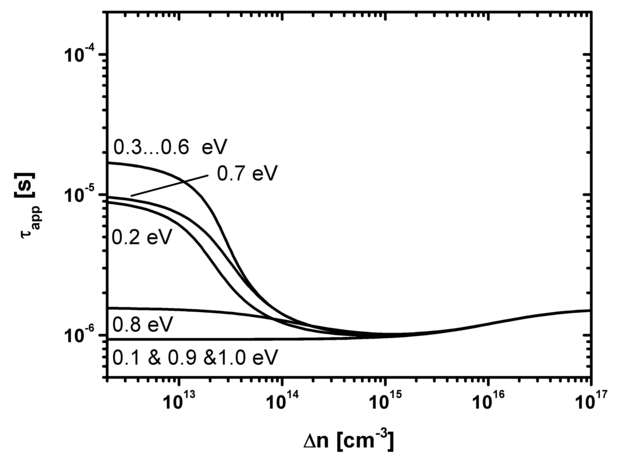
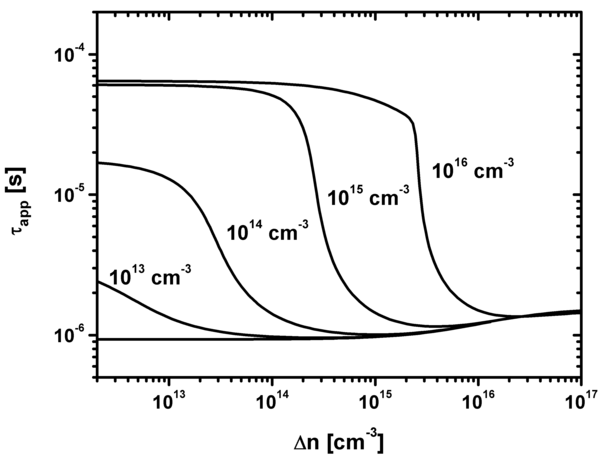
Рис. 7. Изменение параметра E_T (энергия активации).

Рис. 8. Изменение параметра N_T (плотность дефектов).

Рис. 9. Изменение параметра σ_p (поперечное сечение захвата).

Имитационная модель профилей носителей заряда

Профиль глубины носителя заряда, который развивается в образце, сильно влияет на измеренное время жизни – именно поэтому необходимо учитывать этот эффект.

Симуляция профилей носителей заряда в толстых образцах

Измерение толстых образцов в виде брусков и слитков всегда приводит к новым вопросам и проблемам. Одним из таких вопросов заключается в том, как профили носителей заряда, которые развиваются в образце, влияют на измерения времени жизни. Чтобы решить эту проблему, был разработан инструмент моделирования для симуляции профилей носителей заряда. Этот инструмент состоит из системы дифференциальных уравнений в частных производных из уравнений переноса для электронов и дырок и уравнения Пуассона:

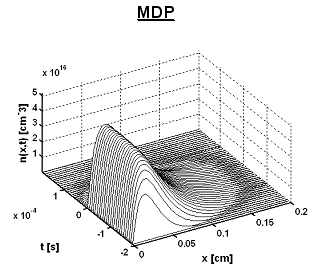
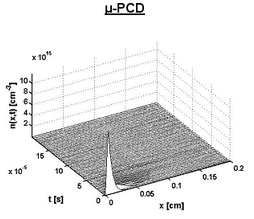
Примеры симуляции для измерений с длинным (типовое состояние для MDP) или очень коротким (типовое состояние для µ-PCD) световым импульсом на толстых непассивированных образцов показаны на рисунках 10 и 11. Становится ясно, что профиль носителя длинного светового импульса расширяется через большой объем образца, тогда как профиль светового импульса длиной всего в 200 нс находится очень близко к поверхности. Это оказывает прямое влияние на измеренное время жизни, поскольку поверхностная рекомбинация оказывает гораздо более сильное влияние на измерения методом µ-PCD.

Рис. 10. Симуляция профиля носителя заряда для типового состояния MDP: длительность импульса 200 мкс; сильное влияние объема образца на результат – профиль уширяется по объему.

Рис. 11. Симуляция профиля носителя заряда для типового состояния µ-PCD: длительность импульса 200 нс; сильное влияние поверхности образца на результат – профиль вблизи поверхности.

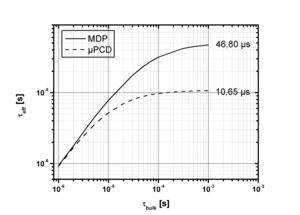
На рис. 12 показано количественное влияние поверхностной рекомбинации на эффективное время жизни для обоих методов измерения. Измерения методом MDP менее подвержены поверхностному воздействию, поэтому больше подходят для исследования объемных свойств. Тогда как метод µ-PCD является идеальным методом для исследования свойств поверхности образца.

Рис. 12. Оценка эффективного времени жизни как функции общего времени жизни для обоих методов.

Источник

Диффузия носителей заряда.

Диффузионная длина

Если в полупроводнике носители заряда распределены неравномерно, возникает диффузия носителей заряда. Она может быть описана известным законом Фика:

Здесь J_p, J_n _ плотности потоков дырок, электронов, равные числу частиц, пересекающих в единицу времени единичную площадку, перпендикулярную направлению градиента концентрации; D_p, D_n – коэффициенты диффузии.

Подвижные носители заряда являются заряженными частицами, поэтому их направленное движение является электрическим током. Плотность тока может быть найдена путем умножения (4.6.1) на элементарный заряд q или (4.6.2) – на (-q)

Если в какой-либо части полупроводника создана избыточная концентрация неравновесных носителей заряда, то одновременно с процессом диффузии происходит их рекомбинация. Поэтому избыточная концентрация уменьшается в направлении от места источника этой избыточной концентрации. Найдем закон изменения избыточной концентрации носителей, например дырок, от расстояния.

В уравнение (4.5.1) – уравнение непрерывности – добавим еще одно слагаемое:

. (4.6.5)

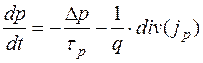
В стационарном случае

, (4.5.6)

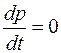
тогда подставим (3) в(5) и приравняем к нулю

; (4.5.7)

после преобразований получим

. (8)

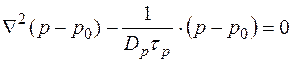
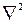
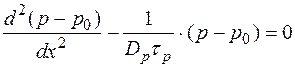
Здесь — оператор Лапласа.

. (4.5.9)

Решение этого уравнения имеет вид

. (4.5.10)

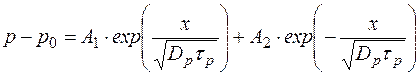
Коэффициенты А₁ и А₂ найдем из граничных условий.

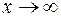
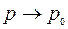
При , откуда А₁=0;

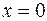
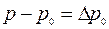
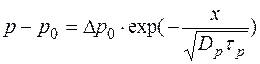
при ,откуда А₂= Dp₀.

(4.5.11)

. (4.5.12)

Здесь 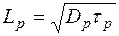— диффузионная длина.

Расстояние, на котором пpи одномерной диффузии в полупpоводнике без электрического поля в нем избыточная концентpация носителей заряда уменьшается вследствие рекомбинации в е раз, называют диффузионной длиной. Можно показать, что диффузионная длина pавна среднему расстоянию, на которое диффундируют носители за вpемя жизни.

Замечание: не следует путать диффузионную длину ни со средней длиной свободного пробега носителей, которая определяется как среднее расстояние, проходимое носителем между двумя последовательными актами рассеяния, ни с длиной волны де Бройля, равной h/mv.

Диффузионная длина очень важна, её вносят в марку материала.

Источник

Что называется диффузионной длиной

Диффузия носителей заряда

Если по какой-то причине концентрация n носителей заряда в полупроводнике неоднородна, то возникает градиент концентрации носителей:

Наличие градиента концентрации приводит к диффузии— движению носителей заряда из области с большей концентрацией в область с меньшей концентрацией, приводящее к выравниванию концентрации носителей заряда по полупроводнику.

Диффузия не связана с электрическим зарядом свободных носителей. Она наблюдается и для нейтральных частиц, например, молекул газа или атомов в твердых телах при нагреве их до достаточно высокой температуры.

В одномерном случае плотность потока частиц при диффузии выражается первым законом Фика :

где D_n – коэффициент диффузии электронов.

Диффузионный ток дырок

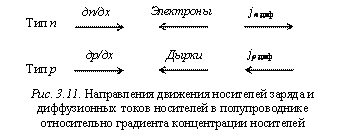
Диффузионный ток электронов совпадает с направлением вектора градиента концентрации электронов, а диффузионный ток дырок противоположен направлению вектора градиента концентрации дырок (рис. 3.11).

Между коэффициентами диффузии и подвижностями носителей заряда существует взаимосвязь, выражаемая соотношениями Эйнштейна. Коэф­фи­циент диф­­фузии D связан с подвижностью носителей за­ряда m со­отношением Эйнштейна. Для электронов

Соотношение Эйнштейна для дырок:

Зависимость подвижности и коэффициента диффузии от типа носителей заряда и материала полупроводника. Из соотношений Эйнштейна (3.23) следует пропорциональная связь между коэффициентом диффузии носителей заряда и их подвижностью.

Величина подвижности, и, следовательно, коэффициента диффузии зависят от материала полупроводника, в частности, от ширины его запрещенной зоны. В таблице 3.1 приведены значения коэффициентов диффузии и подвижностей для основных полупроводников.

Источник