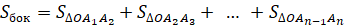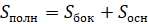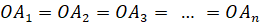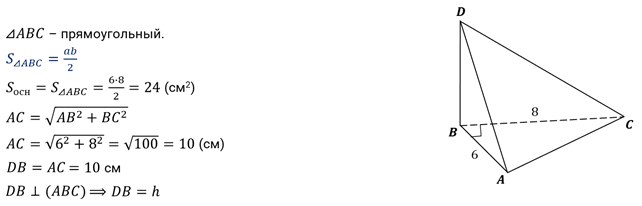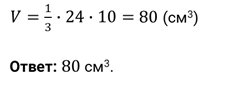Что называется диагональным сечением пирамиды
Пирамида
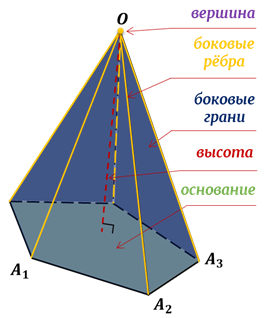
Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.
Основание — многоугольник, которому не принадлежит вершина пирамиды.
Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.
Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).
Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.
Некоторые свойства пирамиды
1) Если все боковые ребра равны, то
– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр
– боковые ребра образуют с плоскостью основания равные углы
Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.
Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
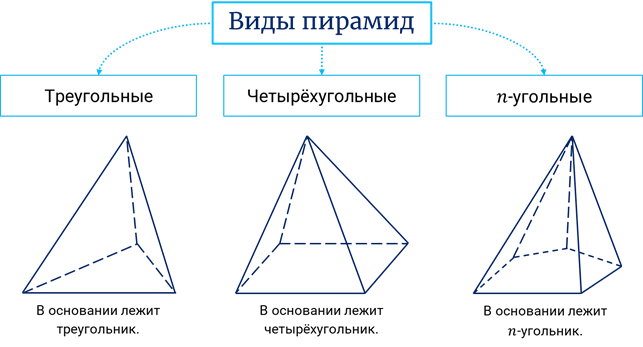
Виды пирамид
Для правильной пирамиды справедливо:
– боковые ребра правильной пирамиды равны;
– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;
– в любую правильную пирамиду можно вписать сферу;
– около любой правильной пирамиды можно описать сферу;
– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
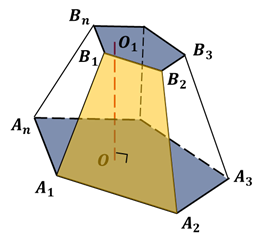
Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.
Что называется диагональным сечением пирамиды
Диагональное сечение параллелепипеда – это сечение плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.
Это сечение всегда представляет собой прямоугольник или квадрат.
Диагональное сечение разбивает параллелепипед на две призмы
Диагональным сечением пирамиды называется сечение её плоскостью, проходящей через два боковых ребра пирамиды, не лежащих в одной грани.
Это сечение всегда представляет собой треугольник.
Любое диагональное сечение разбивает пирамиду на две пирамиды..
Осевое сечение фигуры – это сечение, которое проходит через ось фигуры и перпендикулярно основанию.
Осевое сечение конуса – это всегда равнобедренный треугольник.
Осевое сечение усеченного конуса – равнобедренная трапеция
Осевое сечение цилиндра – прямоугольник. Любое сечение, параллельное осевому – тоже прямоугольник.
3. Сечения плоскостью, параллельной основанию
3.1. Сечение цилиндра плоскостью, параллельной его основаниям
Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.
3.2. Сечение конуса плоскостью, параллельной его основанию
Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковая поверхность – по окружности с центром на оси конуса.
О – Центр шара, В – центр круга сечения.
Самое большой сечение шара – сечение, проходящее через его центр
Геометрические фигуры. Пирамида.
Пирамида — многогранник, в основании которого лежит многоугольник, а остальные грани являются треугольниками, которые имеют общую вершину. Пирамида – это частный случай конуса.
Элементы пирамиды.
Свойства пирамиды.
1. Когда все боковые ребра имеют одинаковую величину, тогда:
2. Когда боковые грани имеют угол наклона к плоскости основания одной величины, тогда:
3. Около пирамиды можно описать сферу в том случае, если в основании пирамиды лежит многоугольник, вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы станет точка пересечения плоскостей, которые проходят через середины ребер пирамиды перпендикулярно им. Из этой теоремы делаем вывод, что как около всякой треугольной, так и около всякой правильной пирамиды можно описать сферу.
4. В пирамиду можно вписать сферу в том случае, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в 1-ной точке (необходимое и достаточное условие). Эта точка станет центром сферы.
5. Конус будет вписанным в пирамиду, когда вершины их совпадут, а основание конуса будет вписанным в основание пирамиды. При этом вписать конус в пирамиду можно лишь в том случае, если апофемы пирамиды имеют равные величины (необходимое и достаточное условие).
6. Конус будет описанным около пирамиды, если их вершины совпадут, а основание конуса будет описано около основания пирамиды. При этом описать конус около пирамиды можно лишь в том случае, если все боковые ребра пирамиды имеют одинаковые величины (необходимое и достаточное условие). Высоты у этих конусов и пирамид одинаковы.
7. Цилиндр будет вписанным в пирамиду, если 1-но его основание совпадет с окружностью, которая вписана в сечение пирамиды плоскостью, параллельной основанию, а второе основание будет принадлежать основанию пирамиды.
8. Цилиндр будет описанным около пирамиды, когда вершина пирамиды будет принадлежать его одному основанию, а второе основание цилиндра будет описано около основания пирамиды. При этом описать цилиндр около пирамиды можно лишь в том случае, если основанием пирамиды служит вписанный многоугольник (необходимое и достаточное условие).
Виды пирамид.
По количеству углов основания пирамиды делят на треугольные, четырехугольные и так далее.
Пирамида будет треугольной, четырехугольной, и так далее, когда основанием пирамиды будет треугольник, четырехугольник и так далее. Треугольная пирамида есть четырехгранник — тетраэдр. Четырехугольная — пятигранник и так далее.
Что такое пирамида: определение, элементы, виды, варианты сечения
В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения пирамиды. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
Определение пирамиды
Пирамида – это геометрическая фигура в пространстве; многогранник, который состоит из основания и боковых граней (с общей вершиной), количество которых зависит от количества углов основания.
Примечание: пирамида – это частный случай конуса.
Элементы пирамиды
Развёртка пирамиды – фигура, полученная при “разрезе” пирамиды, т.е. при совмещении всех ее граней в плоскости одной из них. Для правильной четырехугольной пирамиды развертка в плоскости основания выглядит следующим образом.
Примечание: свойства пирамиды представлены в отдельной публикации.
Виды сечения пирамиды
1. Диагональное сечение – секущая плоскость проходит через вершину фигуры и диагональ основания. У четырехугольной пирамиды таких сечения два (по одному на каждую диагональ):
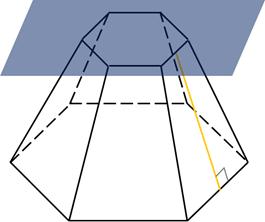
2. Если секущая плоскость параллельна основанию пирамиды, она делит ее на две фигуры: подобную пирамиду (считая от вершины) и усеченную пирамиду (считая от основания). Сечением является подобный основанию многоугольник.
Примечание: Существуют и другие виды сечения, но они не так распространены.
Пирамида. Площади поверхностей. Объём
Урок 36. Подготовка к ЕГЭ по математике
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Пирамида. Площади поверхностей. Объём»
Напомним, что пирамида – это многогранник, в основании которого лежит 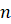
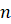
Многоугольник 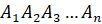
Треугольники 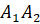
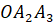
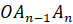
Точка 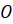
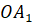
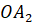
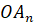
Отрезок, соединяющий вершину пирамиды с плоскостью её основания и перпендикулярный к этой плоскости, называется высотой пирамиды.
Пирамиду с вершиной 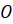
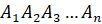
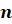
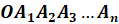
Диагональное сечение – это сечение пирамиды плоскостью, которая проходит через два боковых ребра, не принадлежащих одной грани.
Объединение боковых граней называется боковой поверхностью пирамиды, а объединение всех граней называется полной поверхностью пирамиды.
Тогда площадью боковой поверхности пирамиды называется сумма площадей её боковых граней.
А площадью полной поверхности пирамиды называется сумма площадей всех её граней.
Объём пирамиды равен:
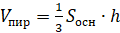
Пирамида, в зависимости от того, какой многоугольник лежит в основании, имеет своё название.
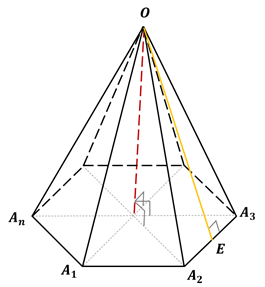
Пирамида называется правильной, если её основанием является правильный многоугольник, а все боковые рёбра равны.
Отрезок, соединяющий вершину пирамиды с центром основания, является её высотой.
Высота боковой грани правильной пирамиды, проведённая из её вершины к ребру основания, называется апофемой.
Выше изображена правильная пирамида. 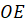
Отметим некоторые свойства правильной 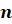
1. В правильной 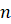
2. Боковые рёбра равно наклонены к основанию.
3. Из равенства боковых рёбер пирамиды следует и равенство её боковых граней.
4. Боковые грани равно наклонены к основанию.
5. Вершина проектируется в центр основания (основание высоты совпадает с центром основания).
6. Площадь боковой поверхности правильной пирамиды равна:
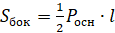
7. Объём правильной четырёхугольной пирамиды со стороной основания 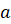
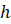
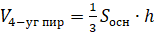
Параллельное сечение пирамиды – сечение пирамиды плоскостью, параллельной основанию.
Параллельное сечение пирамиды обладает следующими свойствами:
1. сечение, параллельное основанию пирамиды, отсекает на высоте пирамиды и боковых рёбрах пропорциональные отрезки;
2. в сечении получается многоугольник, подобный основанию;
3. площади сечения и основания относятся как квадраты их расстояний до вершины.
Усечённая пирамида – это часть пирамиды, заключённая между основанием и параллельным сечением пирамиды.
Основания усечённой пирамиды – подобные многоугольники, лежащие в параллельных плоскостях.
Боковые грани усечённой пирамиды – трапеции.
Высота усечённой пирамиды – это перпендикуляр, опущенный из любой точки верхнего основания на плоскость нижнего.
Площадь полной поверхности усечённой пирамиды равна сумме площади боковой поверхности и площадей двух оснований.
Объём усечённой пирамиды равен разности объёмов полной и отсечённой пирамиды, или его ещё можно вычислить по следующей формуле:
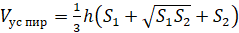
Правильная усечённая пирамида получается из правильной пирамиды.
Апофема – высота боковой грани правильной усечённой пирамиды.
Площадь боковой поверхности правильной усечённой пирамиды равна:
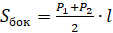
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задача первая. Дана треугольная пирамида, боковые рёбра которой взаимно перпендикулярны и равны 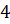
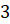
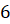
Задача вторая. Дана правильная четырёхугольная пирамида со стороной основания 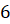
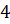
Задача третья. Найдите высоту правильной усечённой треугольной пирамиды 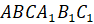
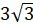
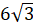
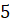
Задача четвёртая. В пирамиде 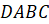
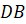
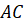
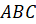
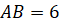
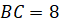
Задача пятая. Найдите объём правильной треугольной пирамиды с ребром основания, равным