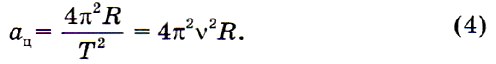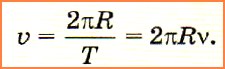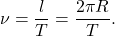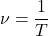Что называется частотой обращения ее формула и частота измерения

Частная школа. 9 класс

Конспекты, контрольные, тесты

Период и частота

Конспект по физике для 9 класса «Период и частота». Что такое период обращения. Что такое частота обращения. Как вычислить скорость и ускорение тела, движущегося по окружности, если известны его период и частота обращения.

Период и частота

Измерить скорость тела, движущегося по окружности, не всегда просто. Однако её можно вычислить, используя такие понятия, как период и частота обращения.

ПЕРИОД

Когда тело движется по окружности с постоянной по модулю скоростью, через определённые промежутки времени движение повторяется снова и снова. Примером этому может служить движение на обычной детской карусели.

Время, в течение которого тело совершает один полный оборот, называют периодом обращения. Период обращения принято обозначать буквой Т. Единица этой физической величины в СИ — секунда.

С понятием периода обращения вы уже знакомились при изучении географии. Например, период обращения Земли вокруг своей оси составляет 23 ч 56 мин 4 с, а период обращения Земли вокруг Солнца — 1,00004 земных года. Самый короткий период обращения вокруг Солнца в нашей Солнечной системе имеет планета Меркурий. Её период обращения составляет 0,24085 земных лет. Интересно, что самая большая планета Солнечной системы — Юпитер — имеет самый короткий период обращения вокруг своей оси — всего 9 ч 50 мин. В 226 000 000 лет оценивается период обращения Солнечной системы вокруг ядра Галактики.

ЧАСТОТА

Число оборотов в единицу времени, которое совершает тело при движении по окружности, называют частотой обращения. Частоту обращения обозначают греческой буквой ν.

Если, катаясь на карусели в парке, мы совершаем один оборот за 20 с, то период обращения в этом случае Т = 20 с. Как определить частоту обращения при этом движении? Сколько оборотов совершает карусель за 1 с?

Очевидно, ν = 1/Т = 1/20 1 /с, т. е. за 1 с карусель совершает одну двадцатую часть своего полного оборота.

Таким образом, частота обращения является величиной, обратной периоду обращения:

СВЯЗЬ МОДУЛЯ СКОРОСТИ С ПЕРИОДОМ И ЧАСТОТОЙ ОБРАЩЕНИЯ

Чтобы определить модуль скорости тела, движущегося по окружности, достаточно знать радиус окружности R и период или частоту обращения. Действительно, один полный оборот тело совершает за время, равное периоду обращения Т. Путь, пройденный телом, в этом случае равен длине окружности: l = 2πR. Тогда можно записать:

или с учётом формулы (1):

С учётом формул (2) и (3) можно найти центростремительное ускорение тела, выразив скорость через период или частоту обращения:

Часто мгновенную скорость движения по окружности называют линейной скоростью.

Модуль скорости движения тела по окружности рассчитывается по формуле:

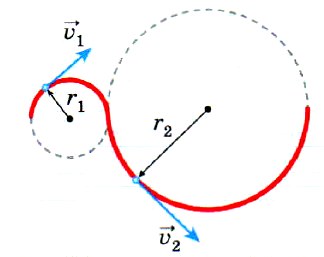
Умение описывать движение тела по окружности чрезвычайно важно, так как движение по криволинейной траектории можно приближённо представить как движение по дугам окружностей различных радиусов.

РЕШЕНИЕ ЗАДАЧ

Задача 1. Найдём модуль скорости вращения ребёнка на карусели, если радиус окружности, по которой происходит движение, равен 2,3 м, а время, за которое карусель совершает один полный оборот, равно 20 с.

Ответ: υ = 0,722 м/с.

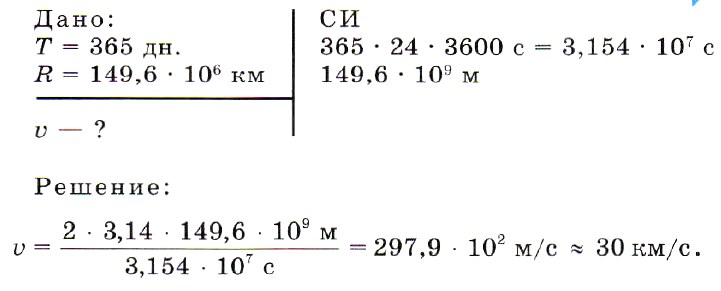
Задача 2. Земля делает один оборот вокруг Солнца за 365 дней. Расстояние от Солнца до Земли составляет 149,6 • 10 6 км. Определим линейную скорость движения Земли вокруг Солнца, считая орбиту окружностью.

Ответ: υ ≈ 30 км/с.

Вы смотрели Конспект по физике для 9 класса «Период и частота».

Источник

Движение по окружности, период обращения и частота.

1. Равномерное движение по окружности

Внимание следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения.

Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу.

Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня.

Во время движения по кругу скорость в любой точке траектории направлена ​​по касательной к окружности в этой точке.

Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время меняется.

2. Период вращения и вращающаяся частота

Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения.

Период обращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот.

Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток.

При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле:

Если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности: . Итак,

Движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой:

частота вращения равна количеству полных оборотов за одну секунду.

Частота вращения и период обращения связаны следующим соотношением:

Частоту в СИ измеряют в

3. Вращательное движение

В природе довольно распространенный вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. Д.

Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусов.

Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу крупнейшего радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.

ПРОВЕРЬТЕ СЕБЯ

1.Равномерное движение по кругу. Внимание учащихся следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения. Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу. Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня. Таким образом, • Во время движения по кругу скорость в любой точке траектории направлена ​​по касательной к окружности в этой точке. Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время изменяется.

2. Период вращения и частота вращения. Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения. • Период вращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот. Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток. При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле: если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности:. Итак, движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой: • вращающаяся частота равна количеству полных оборотов в одну секунду. Частота вращения и период обращения связаны следующим соотношением: Частоту в СИ измеряют в обратных секундах.

3. Вращательного движения. В природе довольно распространенно вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. д.Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусив. Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу самого большого радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.

Источник

Формула частоты

Частота (наряду со временем) является самой точно измеряемой величиной.

Формула частоты колебаний

Единицей измерения частоты в Международной системе единиц (СИ) служат в герцы или обратные секунды:

Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, но близкими по величине частотами ($<\nu >_1\ и\ <\nu >_2$) равна:

Еще одно величиной характеризующей колебательный процесс является циклическая частота ($<\omega >_0$), связанная с частотой как:

Циклическая частота измеряется в радианах, деленных на секунду:

Формула (4) верна для упругих, малых колебаний. Кроме того масса пружины должна быть малой по сравнению с массой тела, прикрепленного к этой пружине.

Для математического маятника частоту колебаний вычисляют как: длина нити:

Физический маятник совершает колебания с частотой:

Формулы для вычисления частоты дискретных событий, частота вращения

Единицей измерения частоты дискретных событий является обратная секунда:

Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.

Примеры задач с решением

Задание. Колебательная система совершила за время равное одной минуте ($\Delta t=1\ мин$) 600 колебаний. Какова частота этих колебаний?

Источник

Частота вращения: формула

Количество повторений каких-либо событий или их возникновения за одну единицу таймера называется частотой. Это физическая величина измеряется в герцах – Гц (Hz). Она обозначается буквами ν, f, F, и есть отношение количества повторяющихся событий к промежутку времени, в течение которого они произошли.

При обращении предмета вокруг своего центра можно говорить о такой физической величине, как частота вращения, формула:

В системе СИ обозначается как – с-1 (s-1) и именуется как обороты в секунду (об/с). Применяют и другие единицы вращения. При описании вращения планет вокруг Солнца говорят об оборотах в часах. Юпитер делает одно вращение в 9,92 часа, тогда как Земля и Луна оборачиваются за 24 часа.

Номинальная скорость вращения

Прежде, чем дать определение этому понятию, необходимо определиться, что такое номинальный режим работы какого-либо устройства. Это такой порядок работы устройства, при котором достигаются наибольшая эффективность и надёжность процесса на продолжении длительного времени. Исходя из этого, номинальная скорость вращения – количество оборотов в минуту при работе в номинальном режиме. Время, необходимое для одного оборота, составляет 1/v секунд. Оно называется периодом вращения T. Значит, связь между периодом обращения и частотой имеет вид:

К сведению. Частота вращения вала асинхронного двигателя – 3000 об./мин., это номинальная скорость вращения выходного хвостовика вала при номинальном режиме работы электродвигателя.

Как найти или узнать частоты вращений различных механизмов? Для этого применяется прибор, который называется тахометр.

Угловая скорость

Когда тело движется по окружности, то не все его точки движутся с одинаковой скоростью относительно оси вращения. Если взять лопасти обычного бытового вентилятора, которые вращаются вокруг вала, то точка расположенная ближе к валу имеет скорость вращения больше, чем отмеченная точка на краю лопасти. Это значит, у них разная линейная скорость вращения. В то же время угловая скорость у всех точек одинаковая.

Угловая скорость представляет собой изменение угла в единицу времени, а не расстояния. Обозначается буквой греческого алфавита – ω и имеет единицу измерения радиан в секунду (рад/с). Иными словами, угловая скорость – это вектор, привязанный к оси обращения предмета.

Формула для вычисления отношения между углом поворота и временным интервалом выглядит так:

Обозначение угловой скорости употребляется при изучении законов вращения. Оно употребляется при описании движения всех вращающихся тел.

Угловая скорость в конкретных случаях

На практике редко работают с величинами угловой скорости. Она нужна при конструкторских разработках вращающихся механизмов: редукторов, коробок передач и прочего.

Вычислить её, применяя формулу, можно. Для этого используют связь угловой скорости и частоты вращения.

В качестве примера могут быть рассмотрены угловая скорость и частота вращения колёсного диска при движении мотоблока. Часто необходимо уменьшить или увеличить скорость механизма. Для этого применяют устройство в виде редуктора, при помощи которого понижают скорость вращения колёс. При максимальной скорости движения 10 км/ч колесо делает около 60 об./мин. После перевода минут в секунды это значение равно 1 об./с. После подстановки данных в формулу получится результат:

ω = 2*π*ν = 2*3,14*1 = 6,28 рад./с.

К сведению. Снижение угловой скорости часто требуется для того, чтобы увеличить крутящий момент или тяговое усилие механизмов.

Как определить угловую скорость

Принцип определения угловой скорости зависит от того, как происходит движение по окружности. Если равномерно, то употребляется формула:

Если нет, то придётся высчитывать значения мгновенной или средней угловой скорости.

Величина, о которой идёт разговор, векторная, и при определении её направления используют правило Максвелла. В просторечии – правило буравчика. Вектор скорости имеет одинаковое направление с поступательным перемещением винта, имеющего правую резьбу.

Рассмотрим на примере, как определить угловую скорость, зная, что угол поворота диска радиусом 0,5 м меняется по закону ϕ = 6*t:

ω = ϕ / t = 6 * t / t = 6 с-1

Вектор ω меняется из-за поворота в пространстве оси вращения и при изменении значения модуля угловой скорости.

Угол поворота и период обращения

Рассмотрим точку А на предмете, вращающимся вокруг своей оси. При обращении за какой-то период времени она изменит своё положение на линии окружности на определённый угол. Это угол поворота. Он измеряется в радианах, потому что за единицу берётся отрезок окружности, равный радиусу. Ещё одна величина измерения угла поворота – градус.

Когда в результате поворота точка А вернётся на своё прежнее место, значит, она совершила полный оборот. Если её движение повторится n-раз, то говорят о некотором количестве оборотов. Исходя из этого, можно рассматривать 1/2, 1/4 оборота и так далее. Яркий практический пример этому – путь, который проделывает фреза при фрезеровании детали, закреплённой в центре шпинделя станка.

Внимание! Угол поворота имеет направление. Оно отрицательное, когда вращение происходит по часовой стрелке и положительное при вращении против движения стрелки.

Если тело равномерно продвигается по окружности, можно говорить о постоянной угловой скорости при перемещении, ω = const.

В этом случае находят применения такие характеристики, как:

Интересно. По известным данным, Юпитер обращается вокруг Солнца за 12 лет. Когда Земля за это время делает вокруг Солнца почти 12 оборотов. Точное значение периода обращения круглого гиганта – 11,86 земных лет.

Циклическая частота вращения (обращения)

Скалярная величина, измеряющая частоту вращательного движения, называется циклической частотой вращения. Это угловая частота, равная не самому вектору угловой скорости, а его модулю. Ещё её именуют радиальной или круговой частотой.

Циклическая частота вращения – это количество оборотов тела за 2*π секунды.

У электрических двигателей переменного тока это частота асинхронная. У них частота вращения ротора отстаёт от частоты вращения магнитного поля статора. Величина, определяющая это отставание, носит название скольжения – S. В процессе скольжения вал вращается, потому что в роторе возникает электроток. Скольжение допустимо до определённой величины, превышение которой приводит к перегреву асинхронной машины, и её обмотки могут сгореть.

Устройство этого типа двигателей отличается от устройства машин постоянного тока, где токопроводящая рамка вращается в поле постоянных магнитов. Большое количество рамок вместил в себя якорь, множество электромагнитов составили основу статора. В трёхфазных машинах переменного тока всё наоборот.

При работе асинхронного двигателя статор имеет вращающееся магнитное поле. Оно всегда зависит от параметров:

Скорость вращения ротора состоит в прямом соотношении со скоростью магнитного поля статора. Поле создаётся тремя обмотками, которые расположены под углом 120 градусов относительно друг друга.

Переход от угловой к линейной скорости

Существует различие между линейной скоростью точки и угловой скоростью. При сравнении величин в выражениях, описывающих правила вращения, можно увидеть общее между этими двумя понятиями. Любая точка В, принадлежащая окружности с радиусом R, совершает путь, равный 2*π*R. При этом она делает один оборот. Учитывая, что время, необходимое для этого, есть период Т, модульное значение линейной скорости точки В находится следующим действием:

Так как ω = 2*π*ν, то получается:

Следовательно, линейная скорость точки В тем больше, чем дальше от центра вращения находится точка.

К сведению. Если рассматривать в качестве такой точки города на широте Санкт-Петербурга, их линейная скорость относительно земной оси равна 233 м/с. Для объектов на экваторе – 465 м/с.

Числовое значение вектора ускорения точки В, движущейся равномерно, выражается через R и угловую скорость, таким образом:

а = ν2/ R, подставляя сюда ν = ω* R, получим: а = ν2/ R = ω2* R.

Это значит, чем больше радиус окружности, по которой движется точка В, тем больше значение её ускорения по модулю. Чем дальше расположена точка твердого тела от оси вращения, тем большее ускорение она имеет.

Поэтому можно вычислять ускорения, модули скоростей необходимых точек тел и их положений в любой момент времени.

Понимание и умение пользоваться расчётами и не путаться в определениях помогут на практике вычислениям линейной и угловой скоростей, а также свободно переходить при расчётах от одной величины к другой.

Видео

Источник

Частота

Определение частоты

Частотой называют физическую величину, характеризующую периодический процесс.

Частота колебаний

Частота служит одним из основных параметров, характеризующих колебания.

В Международной системе единиц (СИ) частота измеряется в герцах или обратных секундах:

Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, о близкими по величине частотами ($<\nu >_1\ и\ <\nu >_2$) равна:

Другой характеристикой колебаний является циклическая частота, которая равна:

Циклическая частота измеряется в радианах, деленных на секунду:

Выражение (4) выполняется для упругих, малых колебаний. Масса пружины должна быть мала в сравнении с массой тела.

Частота колебаний физического маятника:

Частота дискретных событий, частота вращения

Единицей измерения частоты дискретных событий является обратная секунда:

Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.

Примеры задач с решением

Решение. Рассмотрим уравнение движения частицы:

Подставим значение циклической частоты, полученное из уравнения (1.1) в формулу (1.3), получаем:

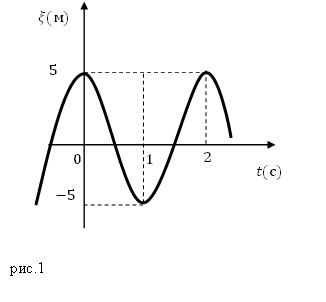
Решение. Сделаем рисунок.

В нашей задаче мы имеем колебания пружинного маятника, частоту которого можно найти как:

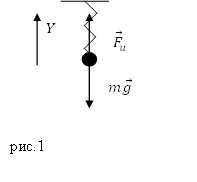
Рассмотрим состояние равновесия тела, которое прикреплено к пружине (рис.1). Запишем второй закон Ньютона для сил, действующих на это тело в состоянии равновесия:

Запишем проекцию уравнения (2.2) на ось Y:

Так как колебания груза на пружине малые, то выполняется закон Гука и мы можем считать, что:

\[F_u=k\Delta x\ \left(2.4\right).\]

Подставим полученный в (2.5) результат в (1.1), частота колебаний тела на пружине равна:

Источник