Что называется арктангенсом числа а

Обратные тригонометрические функции и их графики

Обратные тригонометрические функции — это арксинус, арккосинус, арктангенс и арккотангенс.

Сначала дадим определения.

Расскажем подробно об этих четырех новых для нас функциях — обратных тригонометрических.

Например, арифметический квадратный корень из числа а — такое неотрицательное число, квадрат которого равен а.

Логарифм числа b по основанию a — такое число с, что

Мы понимаем, для чего математикам пришлось «придумывать» новые функции. Например, решения уравнения — это и Мы не смогли бы записать их без специального символа арифметического квадратного корня.

Понятие логарифма оказалось необходимо, чтобы записать решения, например, такого уравнения: Решение этого уравнения — иррациональное число Это показатель степени, в которую надо возвести 2, чтобы получить 7.

Так же и с тригонометрическими уравнениями. Например, мы хотим решить уравнение

Ясно, что его решения соответствуют точкам на тригонометрическом круге, ордината которых равна И ясно, что это не табличное значение синуса. Как же записать решения?

Здесь не обойтись без новой функции, обозначающей угол, синус которого равен данному числу a. Да, все уже догадались. Это арксинус.

А вторая серия решений нашего уравнения — это

Подробнее о решении тригонометрических уравнений — здесь.

Повторим определение еще раз:

Мы готовы построить график функции

Как обычно, отмечаем значения х по горизонтальной оси, а значения у — по вертикальной.

Значит, областью определения функции y = arcsin x является отрезок

Заметим, что график функции y=arcsinx весь помещается в области, ограниченной линиями и

Как всегда при построении графика незнакомой функции, начнем с таблицы.

Строим график функции

1. Область определения

2. Область значений

Напомним, что графики взаимно обратных функций симметричны относительно прямой

Аналогично, определим функцию Только отрезок нам нужен такой, на котором каждому значению угла соответствует свое значение косинуса, а зная косинус, можно однозначно найти угол. Нам подойдет отрезок

Арккосинусом числа a называется число , такое, что

Легко запомнить: «арккосинусы живут сверху», и не просто сверху, а на отрезке

Обозначение: Область определения арккосинуса — отрезок Область значений — отрезок

Арккосинус не является ни чётной, ни нечётной функцией. Зато мы можем использовать следующее очевидное соотношение:

Построим график функции

Заполним таблицу, пользуясь определением арккосинуса.

Вот график арккосинуса:

1. Область определения

2. Область значений

Эта функция общего вида — она не является ни четной, ни нечетной.

5. Функции и являются взаимно обратными.

Следующие — арктангенс и арккотангенс.

Арктангенсом числа a называется число , такое, что

Дальше рассуждаем так же, как при построении графиков арксинуса и арккосинуса.

А что же будет при бесконечно больших значениях х? Другими словами, как ведет себя эта функция, если х стремится к плюс бесконечности?

Мы можем задать себе вопрос: для какого числа из интервала значение тангенса стремится к бесконечности? — Очевидно, это

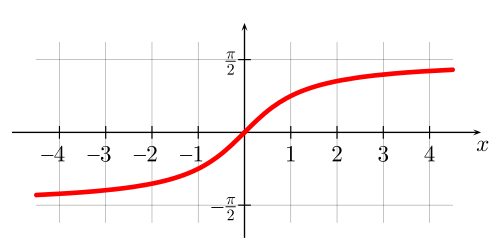
А значит, при бесконечно больших значениях х график арктангенса приближается к горизонтальной асимптоте

Аналогично, если х стремится к минус бесконечности, график арктангенса приближается к горизонтальной асимптоте

На рисунке — график функции

1. Область определения

2. Область значений

3. Функция нечетная.

4. Функция является строго возрастающей.

5. Прямые и — горизонтальные асимптоты данной функции.

6. Функции и являются взаимно обратными — конечно, когда функция рассматривается на промежутке

Аналогично, определим функцию арккотангенс и построим ее график.

Арккотангенсом числа a называется число , такое, что

1. Область определения

2. Область значений

4. Функция является строго убывающей.

5. Прямые и — горизонтальные асимптоты данной функции.

6. Функции и являются взаимно обратными, если рассматривать на промежутке

Источник

Арксинус, арккосинус, арктангенс и арккотангенс числа: основные свойства

Синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса

Это свойство используется чаще всего, поэтому логичнее всего начать рассмотрение всех основных свойств именно с него. Рассмотрим, чему равны синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса числа.

Синус арксинуса, косинус арккосинуса, тангенс арктангенса и котангенс арккотангенса числа

Данное свойство следует напрямую из определения арксинуса, арккосинуса, арктангенса и арккотангенса.

sin ( a r c sin a ) = a

Доказательство для арккосинуса, арктангенса и арккотангенса строится аналогично, на базе определений этих функций. Вот несколько примеров использования данного свойства.

Пример 1. Свойства обратных тригонометрических функций

Арксинус, арккосинус, арктангенс и арккотангенс противоположных чисел

Существует связь между арксинусами, арккосинусами, арктангенсами и арккотангенсами противоположных чисел. Запишем соотношения, выражающие ее.

arcsin, arccos, arctg и arcctg противоположных чисел

Доказательство свойства арксинусов противоположных чисел завершено.

Теперь рассмотрим доказательство свойства арккосинусов противоположных чисел.

Доказательства для арктангенса и арккотангенса проводится по аналогичному принципу.

Сумма арксинуса и арккосинуса, арктангенса и арккотангенса

Данное свойство устанавливает связь соответственно между арксинусом и арккосинусам, арктангенсом и арккотангенсом. Запишем формулы для арксинуса и арккосинуса.

Сумма arcsin и arccos

Соответственно, для арктангенса и арккотангенса

Сумма arctg и arcctg

Пользуясь разобранными свойствами, можно выряжать арксинус через арккосинус, арккосинус через арксинус, арктангенс через арккотангенс и наоборот.

Пример 2. Сумма арксинуса и арккосинуса

Арксинус синуса, арккосинус косинуса, арктангенс тангенса и арккотангенс котангенса

Запишем соотношения, иллюстрирующие свойства арксинуса синуса, арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса.

Свойства арксинуса синуса, арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса

Аналогично, соблюдение условий обязательно для арккосинуса косинуса, арктангенса тангенса и арккотангенса котангенса.

К примеру, запись a r c sin ( sin 8 π 3 ) = 8 π 3 будет ошибочной, так как число 8 π 3 не удовлетворяет условиям неравенства.

Описанные в этой статье свойства позволяют получить ряд полезных формул, определяющих связи между основными и обратными тригонометрическими функциями. Соотношениям, связывающим sin, cos, tg, ctg, arcsin, arccos, arctg и arcctg будет посвящена отдельная статья.

Источник

Арксинус, арккосинус, арктангенс и арккотангенс – начальные сведения

Задача, обратная нахождению значения синуса, косинуса, тангенса и котангенса данного угла (числа), подразумевает нахождение угла (числа) по известным значениям тригонометрических функций. Она приводит к понятиям арксинуса, арккосинуса, арктангенса и арккотангенса числа.

В этой статье мы дадим определения арксинуса, арккосинуса, арктангенса и арккотангенса числа, введем принятые обозначения, а также приведем примеры арксинуса, арккосинуса, арктангенса и арккотангенса. В заключение упомянем про аркфункции и покажем, как арксинус, арккосинус, арктангенс и арккотангенс связаны с единичной окружностью.

Навигация по странице.

Определения, обозначения, примеры

Арксинус, арккосинус, арктангенс и арккотангенс можно определить как угол и как число. Это связано с тем, что мы определили синус, косинус, тангенс и котангенс как угла, так и числа (смотрите синус, косинус, тангенс и котангенс в тригонометрии). Остановимся на обоих подходах к определению арксинуса, арккосинуса, арктангенса и арккотангенса.

Арксинус, арккосинус, арктангенс и арккотангенс как угол

Аналогично определяются арккосинус, арктангенс и арккотангенс.

В свете введенных обозначений, определения арксинуса, арккосинуса, арктангенса и арккотангенса числа можно записать более формально:

Теперь можно привести примеры арксинуса, арккосинуса, арктангенса и арккотангенса числа.

Арксинус, арккосинус, арктангенс и арккотангенс как число

Когда мы имеем дело с синусом, косинусом, тангенсом и котангенсом угла, то естественно арксинус, арккосинус, арктангенс и арккотангенс определять как угол. Если же мы начинаем говорить про синус, косинус, тангенс и котангенс числа, а не угла, то естественно арксинус, арккосинус, арктангенс и арккотангенс определять уже как число.

Источник

Арксинус, арккосинус, арктангенс и арккотангенс числа

Арккотангенс

Arcctg числа a – принимает такое значение α из интервала (0; π), что его котангенс равен а.

Свойства функции арккотангенса:

Сопоставить ctg x и arctg x очень просто, нужно лишь сделать два рисунка и описать поведение кривых.

Задание 2. Соотнести график и форму записи функции.

Если рассуждать логически, из графиков видно, что обе функции возрастающие. Следовательно, оба рисунка отображают некую функцию arctg. Из свойств арктангенса известно, что y=0 при x = 0,

Ответ: рис. 1 – 1, рис. 2 – 4.

Видео

Решение уравнения cosx = a

Рассмотрим тригонометрическое уравнение, в левой части которого стоит ф-ция cosx, а в правой – число, например, 0,5:

По определению арккосинуса очевидно, что arccos 0,5 будет его решением, ведь

Так как arccos 0,5 = π/3, то мы находим очевидный корень х = π/3. И действительно, если подставить это значение в исходное ур-ние, то получится верное равенство:

Значит ли это, что мы решили ур-ние? Нет, ведь мы нашли только один корень, а их может быть несколько. Проведем на единичной окружности вертикальную прямую х = 0,5 и посмотрим, где она пересечет окружность:

Видно, что есть ещё одна точка пересечения, соответствующая углу (– arccos 0,5). Это значит, что этот угол также является решением ур-ния. Проверим это:

Здесь мы использовали тот факт, косинус – четная функция, то есть

Итак, число – π/3 также является корнем ур-ния. Есть ли ещё какие-нибудь корни? Оказывается, есть. Построим график ф-ции у = cosx и посмотрим, где ее пересекает прямая у = 0,5:

Оказывается, прямая пересекает график в бесконечном количестве точек! Это связано с периодичностью ф-ции у = cosx. Период этой ф-ции равен 2π, то есть

Поэтому, если число π/3 является решением ур-ния, то так же решением будут и число π/3 + 2π. Но к этому числу можно ещё раз добавить 2π и получить число π/3 + 4π. И оно тоже будет корнем. С другой стороны, период можно не только добавлять, но и вычитать, поэтому корнями ур-ния окажутся числа π/3 – 2π, π/3 – 4π и т.д. Как же записать все эти бесчисленные решения? Для этого используется такая запись:

Запись «π/3+ 2πn» называется серией решений. Она включает в себя бесконечное количество значений х, которые обращают ур-ние в справедливое равенство. Достаточно выбрать любое целое число и подставить его в серию решений. Например, при n = 0 получим решение

При n = 5 получим корень

При n = – 10 у нас получится решение

Однако помимо серии х = π/3 + 2πn решениями ур-ния будет определять ещё одна серия:

Действительно, число (– π/3) является корнем, но не входит в первую серию. Поэтому оно порождает собственную серию корней. Так, подставив в эту серию n = 4, получим корень

Итак, решением ур-ния являются две серии решений. Заметим, что каждой серии решений с периодом 2π соответствует ровно одна точка на единичной окружности:

Объединить же обе серии можно одной записью:

Напомним, что мы решали ур-ние

и получили для него решение

Число π/3 появилось в записи по той причине, что arccos 0,5 = π/3. Поэтому в общем случае, когда ур-ние имеет вид

где а – некоторое число, его решением будут все такие х, что

Для краткости запись «n– целое число» заменяют эквивалентной записью

Напомним, что буквой Z обозначают множество целых чисел.

Задание. Решите ур-ние

Решение. Вспомним, что

Задание. Решите ур-ние

Решение. В таблице стандартных углов нет такого числа, у которого косинус равен 0,25. Поэтому вычислить значение arccos 0,25 мы не сможем. Но для записи решения и не нужно его вычислять:

Иногда встречаются задачи, в которых надо не просто решить ур-ние, но и выбрать некоторые его корни, удовлетворяющие определенному условию. Процедуру выбора корней, удовлетворяющих условию задачи, часто называют отбором корней. Заметим, что иногда при отборе корней удобнее записывать решение ур-ние не в виде одной серии, а в виде двух серий, у каждой из которых период равен 2π. Рассмотрим отбор корней на примере.

Задание. Укажите три наименьших положительных корня ур-ния

то все решения образуют две серии:

Начнем подставлять вместо n целые числа и выпишем из каждой серии несколько чисел. Так мы сможем найти наименьшие положительные числа в каждой серии.

Отметим все найденные корни на координатной прямой (схематично, не выдерживая масштаб):

Видно, что тремя наименьшими положительными корнями являются числа π/4, 7π/4 и 9π/4

Ответ: π/4, 7π/4 и 9π/4.

Отметим, что возможны три частных случая, когда две серии решений сливаются в одну. Для ур-ния

На графике видно, что этим значениям х соответствуют вершины синусоиды. Решениями же ур-ния

являются точки, в которых график пересекает ось Ох:

Отдельно отметим, что если правая часть в ур-нии – это число, большее единицы или меньшее (– 1), то ур-ние корней не имеет, ведь область определения косинуса – это отрезок [– 1; 1].

Сумма арксинуса и арккосинуса, арктангенса и арккотангенса

Данное свойство устанавливает связь соответственно между арксинусом и арккосинусам, арктангенсом и арккотангенсом. Запишем формулы для арксинуса и арккосинуса.

Сумма arcsin и arccos

arcsin a+arccos a=π2, a∈-1, 1

Соответственно, для арктангенса и арккотангенса

Сумма arctg и arcctg

arctg a+arcctg a=π2, a∈-∞, +∞

≤ a r c cos a ≤ π ≥ — arccos a ≥ — π π 2 ≥ π 2 — arccos a ≥ — π 2 — π 2 ≤ π 2 — arccos a ≤ π 2

sin π 2 — a r c cos a = cos a r c cos a = a

Пользуясь разобранными свойствами, можно выряжать арксинус через арккосинус, арккосинус через арксинус, арктангенс через арккотангенс и наоборот.

Пример 2. Сумма арксинуса и арккосинуса

Известно, что arcsin6-22=π12. Найдем арккосинус этого числа. arcsin6-22+arccos6-22=π2arccos6-22=π2-arcsin6-22arccos6-22=π2-π12=5π12

Решение уравнений tgx = a и ctgx = a

Ур-ния вида tgx = a отличаются тем, что имеют решение при любом значении а. Действительно, построим одну тангенсоиду и проведем горизонтальную линии у = а. При любом а прямая пересечет тангенсоиду, причем ровно в одной точке, которая имеет координаты (arctga; a):

Таким образом, у ур-ния tgx = a существует очевидное решение

Однако напомним, что тангенс является периодической ф-цией, его график представляет собой бесконечное множество тангенсоид, расстояние между которыми равно π. Поэтому корень х = arctga порождает целую серию корней, которую можно записать так:

Задание. Решите ур-ние

Задание. Запишите формулу корней ур-ния

Далее рассмотрим ур-ние вида

Задание. Решите ур-ние

Существует особый случай, когда нельзя заменить котангенс на тангенс. В ур-нии

Из сегодняшнего урока мы узнали про обратные тригонометрические ф-ции – арксинус, арккосинус и арктангенс. Также мы научились находить решения простейших тригонометрических уравнений. Это поможет нам в будущем при изучении более сложных ур-ний.

Источник

Как найти арктангенс: формула, функция, свойства

Понятие арктангенса

Область определения для функции \(y=\operatorname x\) распространяется на всю прямую с числами, не прерывается и обладает ограничениями. Такая функция строго возрастает на графике.

\(\operatorname \,(\operatorname \,x)=x, если при x\in <\mathbb R>,\)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

\(D(\operatorname \,x)=(-\infty ;\infty )\) (область определения),

Функция arctg обладает следующими свойствами, которые полезно использовать при расчете:

Получение функции арктангенса

Предположим, что имеется некая функция:

Заметим, что эта функция имеет вид кусочно-монотонной. Такая ситуация наблюдается на любом участке области определения. В результате нельзя назвать функцией:

Это связано с нарушением условий однозначности. Проанализируем участок, где функция является возрастающей и имеет каждое значение лишь однажды:

Отрезок \(y=\operatorname \,x\) отличается тем, что здесь функция является монотонно возрастающей со всеми своими значениями, которые она принимает только однажды.

График арктангенса

Рассматриваемая аркфункция характеризуется определенным графиком. Изобразить арктангенс на координатной плоскости можно с помощью преображения графика, которому соответствует тангенс. В процессе требуется переместить между собой оси абсцисс и ординат.

График функции \(y=\operatorname \,x\) (можно построить в программе Эксель при вводе нужной формулы):

Арксинус, арккосинус, арктангенс и арккотангенс как число

Обратными функциями в тригонометрии называют такие функции, которые являются обратными к тригонометрическим функциям.

Существует несколько основных аркфункций:

Обратные тригонометрические функции обладают особыми наименованиями. Названия аркфункций формулируют путем приписывания к наименованию функции приставки «арк-».

Функции в тригонометрии отличаются периодичностью. В связи с этим обратные к ним функции обладают множеством значений в виде углов (дуг), для которых конкретная прямая функция определена соответствующим числом.

Под функцией \(\arcsin 1/2\) понимается множество углов \(\left ( \frac<\pi><6>, \frac<5 \pi><6>, \frac<13 \pi><6>, \frac<17 \pi> <6>\dots

(30^\circ, 150^\circ, 390^\circ, 510^\circ \dots) \right ).\)

Если посчитать, синус перечисленных углов соответствует 1/2.

Если рассмотреть множество значений обратной тригонометрической функции, то можно получить ключевые ее значения. Данные значения подразумевают при упоминании арксинуса, арккосинуса и других аркфункций.

Тогда каждое из решений уравнения \(\sin x=\alpha\) допустимо записать, как:

\(x=(-1)^\arcsin \alpha +\pi n,

При нахождении ответов в процессе решения задач, в условии которых присутствуют такие функции, как: синус, косинус, тангенс, котангенс угла, обратные им функции — арксинус, арккосинус, арктангенс, арккотангенс — определяют угол. В том случае, когда речь в задании идет о тригонометрических функциях числа, то аркфункции также будут определяться в виде числа.

Арккосинус числа \(а \in [−1, 1]\) является числом \(t\in [0, \pi]\) с косинусом, равным а.

Арккотангенс числа а \(\in (−\infty, \infty)\) является числом \(t\in (0, \pi)\) с котангенсом, равным а. В данном случае используют знак бесконечности, когда речь идет об определении а.

Важно различать задачи, где аркфункции являются числами, а где — углами. Данное условие можно понять по контексту. Если указана обратная тригонометрическая функция а без каких-либо уточнений, то ее допускается определять, как аркфункцию а в виде угла или числа.

Источник