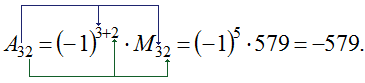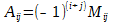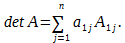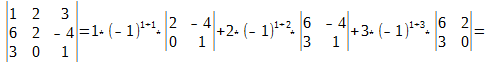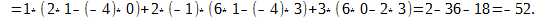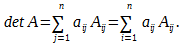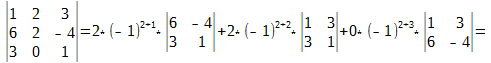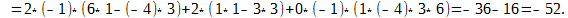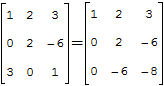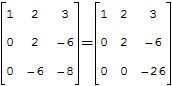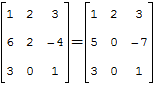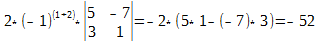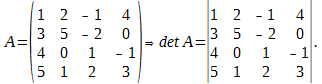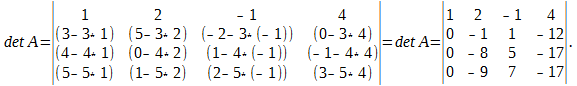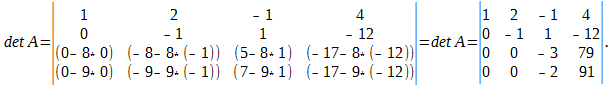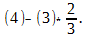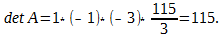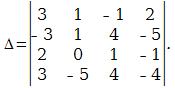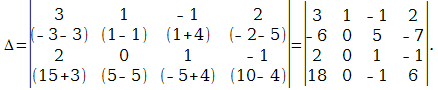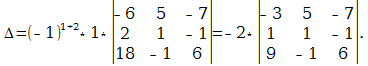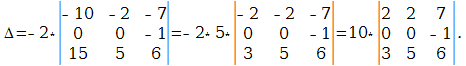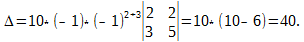Что называется алгебраическим дополнением элемента матрицы

Алгебраические дополнения и миноры. Виды миноров и алгебраических дополнений.

В данной теме рассмотрим понятия алгебраического дополнения и минора. Изложение материала опирается на термины, пояснённые в теме «Матрицы. Виды матриц. Основные термины». Также нам понадобятся некоторые формулы для вычисления определителей. Так как в данной теме немало терминов, относящихся к минорам и алгебраическим дополнениям, то я добавлю краткое содержание, чтобы ориентироваться в материале было проще.

Этот минор несложно вычислить, используя формулу №2 из темы вычисления определителей второго и третьего порядков:

Чтобы найти значение данного минора используем формулу №1 из темы вычисления определителей второго и третьего порядков:

Например, рассмотрим такую матрицу:

Запишем для неё какой-либо минор третьего порядка. Чтобы записать минор третьего порядка нам потребуется выбрать какие-либо три строки и три столбца данной матрицы. Например, возьмём строки №2, №4, №6 и столбцы №1, №2, №4. На пересечении этих строк и столбцов будут располагаться элементы требуемого минора. На рисунке элементы минора показаны синим цветом:

Миноры первого порядка находятся на пересечении одной строки и одного столбца, т.е. миноры первого порядка равны элементам заданной матрицы.

Естественно, что мы могли взять иные строки и столбцы, – например, с номерами 2 и 4, получив при этом иной главный минор второго порядка.

Для примера рассмотрим такую матрицу:

Найдём значение этого минора, используя формулу №2 из темы вычисления определителей второго и третьего порядков:

Данный пример, конечно, тривиальный, так как его цель – наглядно показать суть базисного минора. Вообще, базисных миноров может быть несколько, и обычно процесс поиска такого минора куда сложнее и объёмнее.

Введём ещё одно понятие – окаймляющий минор.

Для примера обратимся к такой матрице:

Запишем минор второго порядка, элементы которого расположены на пересечении строк №2 и №5, а также столбцов №2 и №4. Эти элементы выделены в матрице красным цветом:

Вновь вернёмся к квадратным матрицам. Введём понятие дополнительного минора.

Для примера рассмотрим квадратную матрицу пятого порядка:

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Источник

Минор и алгебраическое дополнение матрицы

Что такое минор и алгебраическое дополнение матрицы

Минор Mij к элементу aij определителя n-го порядка является определителем (n−1)-го порядка, получающимся из начального определителя после исключения i-той строки и j-того столбца.

Исходя из определения, минор представляет собой определитель, который остается после того, как вычеркнуть конкретную строку и конкретный столбец. К примеру, M12 будет получен в результате устранения первой строки и второго столбца. Для того чтобы получить M34 следует вычеркнуть третью строку и четвертый столбец.

Найти миноры с помощью вычерков можно, следуя алгоритму:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Порядок действия при определении алгебраического дополнения следующий:

Общие понятия, основные формулы

Предположим, что существует какая-то квадратная матрица или квадратная матрица n-го порядка:

\(Минор \ M_ \ элемента \ a_ \ матрицы \ A_\) будет являться определитель матрицы, которая получается из матрицы A в результате устранения i-й строки и j-го столбца, которые расположены таким образом, что их пересечение совпадает с элементом \(a_.\)

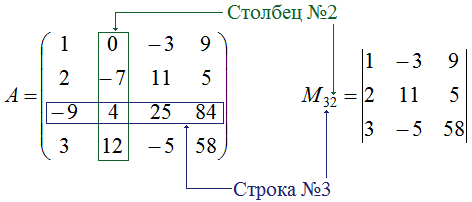
В качестве доказательства можно рассмотреть такую квадратную матрицу четвертого порядка:

Данный минор достаточно просто рассчитать с помощью теоремы для вычисления определителей второго и третьего порядков. Расчет будет следующий:

Таким образом, минор элемента \(a_<32>\) равен 579, то есть \(M_<32>=579\)

Нередко в тематической литературе вместо «минор элемента матрицы» употребляют понятие «минор элемента определителя». Смысл выражения сохраняется. Таким образом, для вычисления минора элемента \(a_\) требуется исключить из начального определителя i-ю строку и j-й столбец. Элементы, которые остались, следует записать в новый определитель, который представляет собой минор элемента \(a_.\)

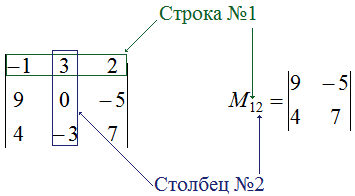
В качестве примера можно рассчитать минор элемента \(a_<12>\) определителя:

Вычислить минор целесообразно с помощью формулы для расчета определителей второго и третьего порядков:

В результате минор элемента \(a_<12>\) составит 83, то есть \(M_<12>=83\)

где \(M_\) является минором элемента \(a_.\)

В качестве примера можно рассчитать алгебраическое дополнение элемента \(a_<32>\) матрицы:

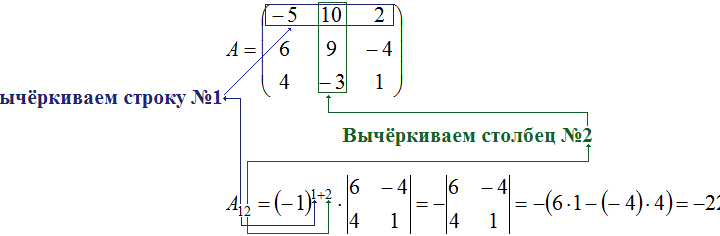
Как правило, при определении алгебраических дополнений не требуется выполнять отдельный расчет минора перед вычислением непосредственно дополнения. К примеру, если требуется определить \(A_<12>\) при условии, что:

Необходимо записать справедливое равенство:

Рассчитать \(M_<12>\) легко с помощью вычерка первой строки и второго столбца матрицы А. Поэтому нет необходимости вводить лишнее обозначение для минора. Достаточно сразу записать уравнение для алгебраического дополнения \(A_<12>\) :

Решение миноров и алгебраических дополнений

Миноры и алгебраические дополнения встречаются в задачах не только с квадратными матрицами, но и прямоугольными. Во втором случае матрицы отличаются тем, что количество строк не обязательно совпадает с количеством столбцов. К примеру, записана матрица:

В рассматриваемой матрице m строк и n столбцов. Минор k-го порядка матрицы \(A_\) представляет собой определитель с элементами, расположенными на пересечении k строк и k столбцов матрицы A. Следует учитывать, что при этом k≤ m и k≤ n.

В качестве примера можно рассмотреть матрицу:

Можно записать для нее какой-то минор третьего порядка. Для этого следует отобрать какие-то три строки и три столбца рассматриваемой матрицы. Выберем для расчета строки №2, №4, №6 и столбцы №1, №2, №4. Данные строки и столбцы будут пересекаться в том месте, где расположены элементы искомого минора.

\(M=\left|\begin 2 & 7 & 6 \\ 0 & 1 & 8 \\ 5 & 3 & 9 \end \right|.\)

Расположение миноров первого порядка будет совпадать с пересечением одной строки и одного столбца. Таким образом, выводим равенство миноров первого порядка элементам рассматриваемой матрицы.

Минор k-го порядка матрицы \(A_=(a_)\) является ключевым в том случае, когда главная диагональ рассматриваемого минора включает исключительно ключевые диагональные элементы матрицы A.

Главные диагональные элементы представляют собой такие элементы матрицы, которые содержат индексы, равные \( a_<11>, a_<22>, a_<33>\) и так далее. К примеру, матрица А, которая рассматривается в примере, содержит элементы \(a_<11>=-1, a_<22>=7, a_<33>=18, a_<44>=8.\)

В том случае, когда в матрице А исключены строки и столбцы, которые соответствуют номерам 1 и 3, их пересечение будет совпадать с элементами минора второго порядка. Главная диагональ этого минора будет содержать лишь диагональные элементы матрицы А. К примеру, такими элементами являются элементы \( a_<11>=-1\) и \(a_<33>=18\) матрицы A. Таким образом, главный минор второго порядка будет равен:

В том случае, если выбрать строки и столбцы с другими номерами, получится другой главный минор второго порядка.

Можно предположить, что какой-то минор M k-го порядка матрицы A_ обладает ненулевым значением, то есть M\neq 0. В данном случае, для всех миноров с порядками выше, чем k, справедливо равенство нулю. Тогда минор M является базисным, а строки и столбцы, содержащие элементы базисного минора, носят названием базисных строк и базисных столбцов.

В качестве примера можно рассмотреть следующую матрицу:

Запись минора рассматриваемой матрицы с элементами, распложенными на месте, где пересекаются строки №1, №2, №3 и столбцы №1, №3, №4, представляет собой минор третьего порядка и имеет следующий вид:

Рассчитать значение искомого минора можно, используя правило для расчета определителей второго и третьего порядков:

Далее можно попытаться записать какой-либо минор с порядком выше, чем 3. Для составления минора четвертого порядка необходимо воспользоваться четвертой строкой, элементы которой имеют нулевые значения. Исходя из этого, можно заключить, что любой минор четвертого порядка обладает нулевой строкой. Таким образом, значение каждого из миноров четвертого порядка равно нулю. Записать миноры пятого порядка и выше не представляется возможным по причине наличия в матрице А всего четырех строк.

По результатам вычислений удалось определить минор третьего порядка с ненулевым значением. Одновременно с этим, миноры более высоких порядков равны нулю, из чего можно сделать вывод: рассматриваемый минор является базисным. Строки №1, №2, №3 матрицы А, которые содержат элементы данного минора, являются базисными строками, а столбцы №1, №3, №4 матрицы А — базисными столбцами.

Пример, который был рассмотрен, является тривиальным. Однако с его помощью удобно продемонстрировать смысл базисного минора. В реальных условиях базисных миноров может быть более одного, а решение подобных задач на нахождение подобного минора существенно сложнее и объемнее.

Еще одним важным термином является окаймляющий минор. Для раскрытия понятия можно предположить, что какой-то минор k-го порядка M матрицы \(A_\) находится в месте, где пересекаются k строки и k столбцы. Если прибавить к совокупности данных строк и столбцов дополнительные строку и столбец, то минор (k+1)-го порядка, который получился в результате, представляет собой окаймляющий минор для минора M.

В качестве примера можно рассмотреть матрицу:

В первую очередь нужно записать минор второго порядка с элементами, расположенными в месте, где пересекаются строки №2 и №5, а также столбцы №2 и №4.

\(M=\left|\begin -17 & 19 \\ 12 & 21 \end \right|\)

К комплекту строк с элементами минора М требуется прибавить одну строку №1, а к столбцам — столбец №5. В результате манипуляций получится новый минор M’ третьего порядка с элементами, расположенными там, где пересекаются строки №1, №2, №5 и столбцы №2, №4, №5.

Минор M’ представляет собой окаймляющий минор для минора M. Таким же образом, путем добавления к комплекту строк с элементами минора М строки №4, а к совокупности столбцов — столбца №3, можно записать минор M», то есть минор третьего порядка.

Минор M», аналогично предыдущему, представляет собой окаймляющий минор для минора M.

Предположим, что существует какой-то минор M k-го порядка матрицы \(A_.\)

Определитель (n-k)-го порядка с элементами, полученными из матрицы A путем исключения строк и столбцов, которые содержали минор M, называется минором, дополнительным к минору M.

В качестве примера можно рассмотреть квадратную матрицу пятого порядка:

В рассматриваемой матрице можно выбрать строки №1 и №3, столбцы №2 и №5. Пересечение данных строк и столбцов будет совпадать с элементами минора М второго порядка.

Далее следует исключить из матрицы А строки №1 и №3, а также столбцы №2 и №5. На пересечении данных компонентов расположены элементы минора М. Элементы, которые остались нетронутыми, сформируют минор M’.

Минор M’ с порядком, соответствующим 5-2=3, представляет собой минор, являющийся дополнительным к минору M.

Запись алгебраического дополнения к минору M квадратной матрицы \(A_\) имеет следующий вид:

В данном случае \alpha является суммой номеров строк и столбцов матрицы A, содержащих элементы минора M, а M’ является дополнительным к минору M. Термин «алгебраическое дополнение к минору M», как правило, формулируют таким образом: «алгебраическое дополнение минора M».

В качестве примера можно рассмотреть матрицу А. Ранее для рассматриваемой матрицы был определен в ходе расчетов минор второго порядка:

Дополнительным к данному минору является такой минор третьего порядка:

В качестве обозначения алгебраического дополнения минора M целесообразно использовать: M^*

Исходя из определения, получим:

Параметр \alpha представляет собой сумму номеров строк и столбцов, которым соответствует минор М. Расположение данного минора соответствует пересечению строк №1, №3 и столбцов №2, №5. Таким образом:

В результате можно записать:

Благодаря формуле для расчета определителей второго и третьего порядков, представляется возможным вычислить алгебраическое дополнение:

Источник

Алгебраическое дополнение матрицы

В данной публикации мы рассмотрим определение и свойства алгебраического дополнения матрицы, приведем формулу, с помощью которой его можно найти, а также разберем пример для лучшего понимания теоретического материала.

Определение и нахождение алгебраического дополнения

Пример
Вычислим алгебраическое дополнение A₃₂ к a₃₂ определителя ниже:

Свойства алгебраического дополнения

1. Если просуммировать произведения элементов произвольной строки и алгебраических дополнений к элементам строки i определителя, то получится определитель, в котором вместо строки i стоит данная произвольная строка.

2. Если просуммировать произведения элементов строки (столбца) определителя и алгебраических дополнений к элементами другой строки (столбца), то получится ноль.

3. Сумма произведений элементов строки (столбца) определителя и алгебраических дополнений к элементам данной строки (столбца) равняется определителю матрицы.

Источник

Что называется алгебраическим дополнением элемента матрицы

Матрицей называют прямоугольную таблицу, заполненную числами. Важнейшие характеристики матрицы – число строк и число столбцов. Если у матрицы одинаковое число строк и столбцов, ее называют квадратной. Обозначают матрицы большими латинскими буквами.

Сами числа называют элементами матрицы и характеризуют их положением в матрице, задавая номер строки и номер столбца и записывая их в виде двойного индекса, причем вначале записывают номер строки, а затем столбца. Например, a₁₄ есть элемент матрицы, стоящий в первой строке и четвертом столбце, a₃₂ стоит в третьей строке и втором столбце.

Главной диагональю квадратной матрицы называют элементы, имеющие одинаковые индексы, то есть те элементы, у которых номер строки совпадает с номером столбца. Побочная диагональ идет «перпендикулярно» главной диагонали.

Особую важность представляют собой так называемые единичные матрицы. Это квадратные матрицы, у которых на главной диагонали стоят 1, а все остальные числа равны 0. Обозначают единичные матрицы E. Матрицы называют равными, если у них равны число строк, число столбцов, и все элементы, имеющие одинаковые индексы, равны. Матрица называется нулевой, если все ее элементы равны 0. Обозначается нулевая матрица О.

Простейшие действия с матрицами

1. Умножение матрицы на число. Для этого необходимо умножить каждый элемент матрицы на данное число.

2. Сложение матриц. Складывать можно только матрицы одинакового размера, то есть имеющие одинаковое число строк и одинаковое число столбцов. При сложении матриц соответствующие их элементы складываются.

4. Умножение матриц. Для произведения матриц существуют следующие свойства:

Свойства произведения матриц:

Определитель матрицы

Определителем (детерминантом) квадратной матрицы А называется число, которое обозначается detA, реже |A| или просто Δ, и вычисляется определённым образом. Для матрицы размера 1х1 определителем является сам единственный элемент матрицы. Для матрицы размера 2х2 определитель находят по следующей формуле:

Миноры и алгебраические дополнения

Рассмотрим матрицу А. Выберем в ней s строк и s столбцов. Составим квадратную матрицу из элементов, стоящих на пересечении полученных строк и столбцов. Минором матрицы А порядка s называют определитель полученной матрицы.

Рассмотрим квадратную матрицу А. Выберем в ней s строк и s столбцов. Дополнительным минором к минору порядка s называют определитель, составленный из элементов, оставшихся после вычеркивания данных строк и столбцов.

Вычисление определителя матрицы через алгебраические дополнения

Рассмотрим квадратную матрицу А. Для вычисления ее определителя необходимо выбрать любую ее строку или столбец и найти произведения каждого элемента этой строки или столбца на алгебраическое дополнение к нему. А дальше надо просуммировать все эти произведения.

Расчет алгебраического дополнения может сводиться к расчету определителя размером более чем 2х2. В этом случае такой расчет также нужно проводить через алгебраические дополнения, и так далее до тех пор, пока алгебраические дополнения, которые нужно будет считать, не станут размером 2х2, после чего воспользоваться формулой выше.

Обратная матрица

Рассмотрим квадратную матрицу А. Матрица A –1 называется обратной к матрице А, если их произведения равны единичной матрице. Обратная матрица существует только для квадратных матриц. Обратная матрица существует, только если матрица А невырождена, то есть ее определитель не равен нулю. В противном случае обратную матрицу посчитать невозможно. Для построения обратной матрицы необходимо:

Таким образом, в случае, если матрица А имеет размер 3х3, обратная к ней матрица имеет вид:

Источник

Как вычислить определитель (детерминант) матрицы? Минор и алгебраическое дополнение

Без преобразования матрицы, определитель легко посчитать только для матриц размером 2×2 и 3×3. Это делается по формулам:

(можно посчитать по любой строке, выше приводиться формула расчёта определителя по первой строке).

Расчёты для матриц размером 4×4 и выше затруднительны, поэтому их нужно преобразовывать в соответствии со свойствами определителя. Нужно стремиться получить матрицу, в которой все значения кроме одного любого столбца или любой строки равны нулю. Пример такой матрицы:

Для неё определитель равен:

Обратите внимание, что

это вычисление детерминанта матрицы, полученой вычетом строки и столбца, на пересечении которых находиться единственное не нулевое числов строки/столбца, по которому мы разлагаем матрицу:

Если привести матрицу к треугольному виду, то её определитель вычисляется как произведение цифр по диагонали. Например, для матрицы

Аналогично следует поступать с матрицами 5×5, 6×6 и другими больших размерностей.

Преобразования матриц нужно выполнять в соответствии со свойствами определителя. Но прежде чем перейти к практике по вычислению определителя для матриц 4×4, давайте вернёмся к матрицам 3×3 и подробно рассмотрим, как вычисляется определитель для них.

Минор

Определитель матрицы не очень прост для понимания, поскольку в его понятии присутствует рекурсия: определитель матрицы состоит из нескольких элементов, в том числе из определителя (других) матриц.

Чтобы не застрять на этом, давайте прямо сейчас (временно) примем, что определитель матрицы

Ещё разберёмся в условных обозначения и в таких понятиях как минор и алгебраическое дополнение.

Буквой i мы обозначаем порядковый номер стоки, буквой j – порядковый номер столбца.

a_ij означает элемент матрицы (цифру) на пересечении строки i и столбца j.

Представим себе матрицу, которая получена из исходной удалением строки i и столбца j. Определитель новой матрицы, которая получена из исходной удалением строки i и столбца j, называется минором M_ij элемента a_ij.

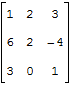
Проиллюстрируем сказанное. Предположим, дана матрица

Тогда для определения минора M₁₁ элемента a₁₁ нам нужно составить новую матрицу, которая получается из исходной удалением первой строки и первого столбца:

И вычислить для неё определитель: 2*1 — (-4)*0 = 2

Для определения минора M₂₂ элемента a₂₂ нам нужно составить новую матрицу, которая получается из исходной удалением второй строки и второго столбца:

Алгебраическое дополнение

Алгебраическим дополнением А_ij для элемента a_ij называется минор M_ij этого элемента, взятый со знаком «+», если сумма индексов строки и столбца (i + j), на пересечении которых стоит этот элемент, чётная, и со знаком «-», если сумма индексов нечётная.

Для матрицы из предыдущего примера

Вычисление определителя для матриц

Определителем порядка n, соответствующим матрице А, называется число, обозначаемое det A и вычисляемое по формуле:

В этой формуле нам всё уже знакомо, давайте теперь посчитаем определитель матрицы для

Каков бы ни был номер строки i=1,2,…, n или столбца j = 1, 2,…, n определитель n-го порядка равен сумме произведений элементов этой строки или этого столбца на их алгебраические дополнения, т. е.

Т.е. детерминант можно вычислить по любому столбцу или по любой строке.

Чтобы убедиться в этом, вычислим определитель для матрицы из последнего примера по второму столбцу

Свойства определителя матриц

Для вычисления определителя любого порядка можно применять метод последовательного понижения порядка определителя. Для этого пользуются правилом разложения определителя по элементам строки или столбца. Еще один способ вычисления определителей заключается в том, чтобы с помощью элементарных преобразований со строками (или столбцами), прежде всего в соответствии со свойствами 4 и 7 определителей, привести определитель к виду, когда под главной диагональю определителя (определяемой так же, как и для квадратных матриц) все элементы равны нулю. Тогда определитель равен произведению элементов, расположенных на главной диагонали.

При вычислении определителя последовательным понижением порядка для уменьшения объема вычислительной работы целесообразно с помощью свойства 7 определителей добиться обнуления части элементов какой-либо строки или какого-либо столбца определителя, что уменьшит число вычисляемых алгебраических дополнений.

Приведение матрицы к треугольному виду, преобразование матрицы, облегчающее вычисление определителя

Показанные ниже методы нецелесообразно использовать для матриц 3×3, но я предлагаю рассмотреть суть методов на простом примере. Воспользуемся матрицей, для которой мы уже считали определитель — нам будет проще проверить правильность вычислений:

Используя 7-е свойство определителя, вычтем из второй строки третью, умноженную на 2:

из третьей строки вычтем соответствующие элементы первой строки определителя, умноженные на 3:

Так как элементы определителя, расположенные под его главной диагональю, равны 0, то, следовательно, определитесь равен произведению элементов, расположенных на главной диагонали:

Как видим, ответ совпал с полученными ранее.

Давайте вспомним формулу определителя матрицы:

Детерминант — это сумма алгебраических дополнений, умноженная на члены одной из строк или одного из столбцов.

Если в результате преобразований мы сделаем так, что одна из строк (или столбец) будет состоять полностью из нулей кроме одной позиции, то нам не нужно будет считать все алгебраические дополнения, поскольку они заведомо будут равны нулю. Как и предыдущий метод, этот целесообразно применять для матриц больших размеров.

Покажем пример на той же самой матрице:

Вычислим определитель по второму столбцу. Нам нужно посчитать только одно алгебраическое дополнение, поскольку остальные заведомо сводятся к нулю:

Вычисление определителя для матриц 4×4, 5×5 и больших размерностей

Чтобы избежать слишком больших вычислений для матриц больших размеров следует делать преобразования, описанные выше. Приведём пару примеров.

Вычислить определитесь матрицы

Р е ш е н и е. Используя 7-е свойство определителя, вычтем из второй строки третью, из четвёртой строки — соответствующие элементы первой строки определителя, умноженные соответственно на 3, 4, 5. Эти действия сокращённо будем обозначать так: (2) — (1) * 3; (3) — (1) * 4; (4) — (1) * 5. Получим:

Далее, в соответствии с ведёнными обозначениями, выполним действия: (3) — (2) * 8; (4) — (2) * 9. Получаем

Так как элементы определителя, расположенные под его главной диагональю, равны 0, то, следовательно, определитесь равен произведению элементов, расположенных на главной диагонали:

Вычислить определитель

Разлагая полученный определитесь по второй строке имеем:

(Затем мы вынесли сомножитель 2 первого столбца на основании свойства 4). Далее прибавим к элементам первого и второго столбца элементы определителя. Получим:

Затем мы вынесли множитель в первом столбце, а затем общий множитель (-1) в первой строке. Разлагая теперь получившийся определитесь третьего порядка по элементам второй строки получим:

Здесь определитесь второго порядка вычислен в соответствии с его определением, по формуле

Вычисление определителя (детерминанта) матрицы wxMaxima и Maxima

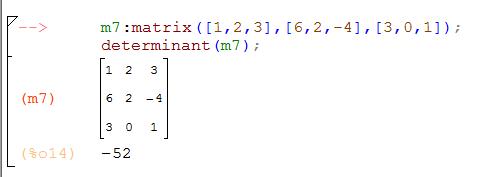
В wxMaxima и Maxima для вычисления определителя используется функция determinant:

Для приведения матриц к треугольному виду можно воспользоваться функцией triangularize:

Источник