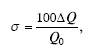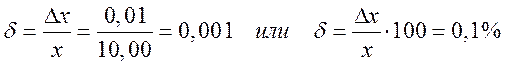Что называется абсолютной относительной систематической и случайной погрешностями измерений

Виды погрешностей. Погрешность измерений. Виды погрешностей

Погрешность измерений. Виды погрешностей.

В практике использования измерений очень важным показателем становится их точность, которая представляет собой ту степень близости итогов измерения к некоторому действительному значению, которая используется для качественного сравнения измерительных операций. А в качестве количественной оценки, как правило, используется погрешность измерений.

Разница между результатом измерения и истинным значением измеряемой величины называется погрешностью измерения.

Причем чем погрешность меньше, тем считается выше точность.

Согласно закону теории погрешностей, если необходимо повысить точность результата (при исключенной систематической погрешности) в 2 раза, то число измерений необходимо увеличить в 4 раза; если требуется увеличить точность в 3 раза, то число измерений увеличивают в 9 раз и т. д.

Процесс оценки погрешности измерений считается одним из важнейших мероприятий в вопросе обеспечения единства измерений. Естественно, что факторов, оказывающих влияние на точность измерения, существует огромное множество. Следовательно, любая классификация погрешностей измерения достаточно условна, поскольку нередко в зависимости от условий измерительного процесса погрешности могут проявляться в различных группах.

Выделяют следующие виды погрешностей:

1) абсолютная погрешность;

2) относительна погрешность;

3) приведенная погрешность;

4) основная погрешность;

5) дополнительная погрешность;

6) систематическая погрешность;

7) случайная погрешность;

8) инструментальная погрешность;

9) методическая погрешность;

10) личная погрешность;

11) статическая погрешность;

12) динамическая погрешность.

Абсолютная погрешность – это значение, вычисляемое как разность между значением величины, полученным в процессе измерений, и настоящим (действительным) значением данной величины.

Абсолютная погрешность вычисляется по следующей формуле:

где AQ_n – абсолютная погрешность;

Q_n – значение некой величины, полученное в процессе измерения;

Q₀ – значение той же самой величины, принятое за базу сравнения (настоящее значение).

Относительная погрешность – это число, отражающее степень точности измерения.

Относительная погрешность вычисляется по следующей формуле:

где ΔQ – абсолютная погрешность;

Q₀ – настоящее (действительное) значение измеряемой величины.

Относительная погрешность выражается в процентах.

Приведенная погрешность – это значение, вычисляемое как отношение значения абсолютной погрешности к нормирующему значению.

Инструментальная погрешность – это погрешность, возникающая из—за допущенных в процессе изготовления функциональных частей средств измерения ошибок.

Методическая погрешность – это погрешность, возникающая по следующим причинам:

1) неточность построения модели физического процесса, на котором базируется средство измерения;

2) неверное применение средств измерений.

Субъективная погрешность – это погрешность возникающая из-за низкой степени квалификации оператора средства измерений, а также из-за погрешности зрительных органов человека, т. е. причиной возникновения субъективной погрешности является человеческий фактор.

Погрешности по взаимодействию изменений во времени и входной величины делятся на статические и динамические погрешности.

Неточность градуировки, конструктивные несовершенства, изменения характеристик прибора в процессе эксплуатации и т. д. являются причинами основных погрешностей инструмента измерения.

Дополнительные погрешности, связанные с отклонением условий, в которых работает прибор, от нормальных, отличают от инструментальных (ГОСТ 8.009-84), т. к. они связаны скорее с внешними условиями, чем с самим прибором.

Систематическая погрешность – это составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. Причинами появления систематической погрешности могут являться неисправности средств измерений, несовершенство метода измерений, неправильная установка измерительных приборов, отступление от нормальных условий их работы, особенности самого оператора.

Статическая погрешность – это погрешность, которая возникает в процессе измерения постоянной (не изменяющейся во времени) величины.

Динамическая погрешность – это погрешность, численное значение которой вычисляется как разность между погрешностью, возникающей при измерении непостоянной (переменной во времени) величины, и статической погрешностью (погрешностью значения измеряемой величины в определенный момент времени).

Случайная погрешность – это составная часть погрешности результата измерения, изменяющаяся случайно, незакономерно при проведении повторных измерений одной и той же величины. Появление случайной погрешности нельзя предвидеть и предугадать. Случайную погрешность невозможно полностью устранить, она всегда в некоторой степени искажает конечные результаты измерений. Но можно сделать результат измерения более точным за счет проведения повторных измерений.

Причиной случайной погрешности может стать, например, случайное изменение внешних факторов, воздействующих на процесс измерения. Случайная погрешность при проведении многократных измерений с достаточно большой степенью точности приводит к рассеянию результатов.

Источник

Погрешность измерений

Неотъемлемой частью любого измерения является погрешность измерений. С развитием приборостроения и методик измерений человечество стремиться снизить влияние данного явления на конечный результат измерений. Предлагаю более детально разобраться в вопросе, что же это такое погрешность измерений.

Погрешность измерения – это отклонение результата измерения от истинного значения измеряемой величины. Погрешность измерений представляет собой сумму погрешностей, каждая из которых имеет свою причину.

По форме числового выражения погрешности измерений подразделяются на абсолютные и относительные

Абсолютная погрешность – это погрешность, выраженная в единицах измеряемой величины. Она определяется выражением.

(1.2), где X — результат измерения; Х₀ — истинное значение этой величины.

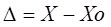
Поскольку истинное значение измеряемой величины остается неизвестным, на практике пользуются лишь приближенной оценкой абсолютной погрешности измерения, определяемой выражением

(1.3), где Х_д — действительное значение этой измеряемой величины, которое с погрешностью ее определения принимают за истинное значение.

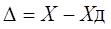
Относительная погрешность – это отношение абсолютной погрешности измерения к действительному значению измеряемой величины:

(1.4)

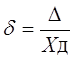
По закономерности появления погрешности измерения подразделяются на систематические, прогрессирующие, и случайные .

Систематическая погрешность – это погрешность измерения, остающаяся постоянной или закономерно изменяющейся при повторных измерениях одной и той же величины.

Прогрессирующая погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени.

Систематические и прогрессирующие погрешности средств измерений вызываются:

Систематическая погрешность остается постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины. Особенность систематической погрешности состоит в том, что она может быть полностью устранена введением поправок. Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. Они требуют непрерывной коррекции.

Случайная погрешность – это погрешность измерения изменяется случайным образом. При повторных измерениях одной и той же величины. Случайные погрешности можно обнаружить только при многократных измерениях. В отличии от систематических погрешностей случайные нельзя устранить из результатов измерений.

По происхождению различают инструментальные и методические погрешности средств измерений.

Инструментальные погрешности — это погрешности, вызываемые особенностями свойств средств измерений. Они возникают вследствие недостаточно высокого качества элементов средств измерений. К данным погрешностям можно отнести изготовление и сборку элементов средств измерений; погрешности из-за трения в механизме прибора, недостаточной жесткости его элементов и деталей и др. Подчеркнем, что инструментальная погрешность индивидуальна для каждого средства измерений.

Методическая погрешность — это погрешность средства измерения, возникающая из-за несовершенства метода измерения, неточности соотношения, используемого для оценки измеряемой величины.

Погрешности средств измерений.

Абсолютная погрешность меры – это разность между номинальным ее значением и истинным (действительным) значением воспроизводимой ею величины:

(1.5), где X_н – номинальное значение меры; Х_д – действительное значение меры

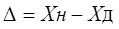
Абсолютная погрешность измерительного прибора – это разность между показанием прибора и истинным (действительным) значением измеряемой величины:

(1.6), где X_п – показания прибора; Х_д – действительное значение измеряемой величины.

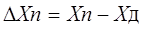
Относительная погрешность меры или измерительного прибора – это отношение абсолютной погрешности меры или измерительного прибора к истинному

(действительному) значению воспроизводимой или измеряемой величины. Относительная погрешность меры или измерительного прибора может быть выражена в ( % ).

(1.7)

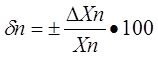
Приведенная погрешность измерительного прибора – отношение погрешности измерительного прибора к нормирующему значению. Нормирующие значение XN – это условно принятое значение, равное или верхнему пределу измерений, или диапазону измерений, или длине шкалы. Приведенная погрешность обычно выражается в ( % ).

(1.8)

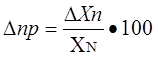
Основная – это погрешность средства измерений, используемого в нормальных условиях, которые обычно определены в нормативно-технических документах на данное средство измерений.

Дополнительная – это изменение погрешности средства измерений вследствии отклонения влияющих величин от нормальных значений.

Статическая – это погрешность средства измерений, используемого для измерения постоянной величины. Если измеряемая величина является функцией времени, то вследствие инерционности средств измерений возникает составляющая общей погрешности, называется динамической погрешностью средств измерений.

Также существуют систематические и случайные погрешности средств измерений они аналогичны с такими же погрешностями измерений.

Факторы влияющие на погрешность измерений.

Погрешности возникают по разным причинам: это могут быть ошибки экспериментатора или ошибки из-за применения прибора не по назначению и т.д. Существует ряд понятий которые определяют факторы влияющие на погрешность измерений

Вариация показаний прибора – это наибольшая разность показаний полученных при прямом и обратном ходе при одном и том же действительном значении измеряемой величины и неизменных внешних условиях.

Класс точности прибора – это обобщенная характеристика средств измерений (прибора), определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на точность, значение которой устанавливаются на отдельные виды средств измерений.

Классы точности прибора устанавливают при выпуске, градуируя его по образцовому прибору в нормальных условиях.

Прецизионность — показывает, как точно или отчетливо можно произвести отсчет. Она определяется, тем насколько близки друг к другу результаты двух идентичных измерений.

Разрешение прибора — это наименьшее изменение измеряемого значения, на которое прибор будет реагировать.

Диапазон прибора — определяется минимальным и максимальным значением входного сигнала, для которого он предназначен.

Полоса пропускания прибора — это разность между минимальной и максимальной частотой, для которых он предназначен.

Чувствительность прибора — определяется, как отношение выходного сигнала или показания прибора к входному сигналу или измеряемой величине.

Шумы — любой сигнал не несущий полезной информации.

Источник

ПОГРЕШНОСТИ ИЗМЕРЕНИЙ

Вследствие погрешностей, присущих средству измерений, выбранному методу и методике измерений, отличия внешних условий, в которых выполняется измерение, от установленных, и других причин результат практически каждого измерения отягощен погрешностью. Эта погрешность вычисляется или оценивается и приписывается полученному результату.

Погрешность результата измерений (кратко — погрешность измерений) — отклонение результата измерения от истинного значения измеряемой величины.

Истинное значение величины вследствие наличия погрешностей остается неизвестным. Его применяют при решении теоретических задач метрологии. На практике пользуются действительным значением величины, которое заменяет истинное значение.

Погрешность измерения (Δх) находят по формуле:

где х_изм. — значение величины, полученное на основании измерений; х_действ. — значение величины, принятое за действительное.

За действительное значение при однократных измерениях нередко принимают значение, полученное с помощью образцового средства измерений, при многократных измерениях — среднее арифметическое из значений отдельных измерений, входящих в данный ряд.

Погрешности измерения могут быть классифицированы по следующим признакам:

— по характеру проявления — систематические и случайные;

— по способу выражения — абсолютные и относительные;

— по условиям изменения измеряемой величины — статические и динамические;

— по способу обработки ряда измерений — средние арифметические и средние квадратические;

— по полноте охвата измерительной задачи — частные и полные;

— по отношению к единице физической величины — погрешности воспроизведения единицы, хранения единицы и передачи размера единицы.

Систематическая погрешность измерения (кратко — систематическая погрешность) — составляющая погрешности результата измерения, остающаяся постоянной для данного ряда измерений или же закономерно изменяющаяся при повторных измерениях одной и той же физической величины.

По характеру проявления систематические погрешности подразделяются на постоянные, прогрессивные и периодические. Постоянные систематические погрешности (кратко — постоянные погрешности) — погрешности, длительное время сохраняющие свое значение (например, в течение всей серии измерений). Это наиболее часто встречающийся вид погрешности.

Прогрессивные систематические погрешности (кратко — прогрессивные погрешности) — непрерывно возрастающие или убывающие погрешности (например, погрешности от износа измерительных наконечников, контактирующих в процессе шлифования с деталью при контроле ее прибором активного контроля).

Периодическая систематическая погрешность (кратко — периодическая погрешность) — погрешность, значение которой является функцией времени или функцией перемещения указателя измерительного прибора (например, наличие эксцентриситета в угломерных приборах с круговой шкалой вызывает систематическую погрешность, изменяющуюся по периодическому закону).

Исходя из причин появления систематических погрешностей, различают инструментальные погрешности, погрешности метода, субъективные погрешности и погрешности вследствие отклонения внешних условий измерения от установленных методиками.

Инструментальная погрешность измерения (кратко — инструментальная погрешность) является следствием ряда причин: износ деталей прибора, излишнее трение в механизме прибора, неточное нанесение штрихов на шкалу, несоответствие действительного и номинального значений меры и др.

Погрешность метода измерений (кратко — погрешность метода) может возникнуть из-за несовершенства метода измерений или допущенных его упрощений, установленных методикой измерений. Например, такая погрешность может быть обусловлена недостаточным быстродействием применяемых средств измерений при измерении параметров быстропротекающих процессов или неучтенными примесями при определении плотности вещества по результатам измерения его массы и объема.

Субъективная погрешность измерения (кратко — субъективная погрешность) обусловлена индивидуальными погрешностями оператора. Иногда эту погрешность называют личной разностью. Она вызывается, например, запаздыванием или опережением принятия оператором сигнала.

Погрешность вследствие отклонения (в одну сторону) внешних условий измерения от установленных методикой измерения приводит к возникновению систематической составляющей погрешности измерения.

Систематические погрешности искажают результат измерения, поэтому они подлежат исключению, насколько это возможно, путем введения поправок или юстировкой прибора с доведением систематических погрешностей до допустимого минимума.

Неисключенная систематическая погрешность (кратко — неисключенная погрешность) — это погрешность результата измерений, обусловленная погрешностью вычисления и введения поправки на действие систематической погрешности, или небольшой систематической погрешностью, поправка на действие которой не введена вследствие малости.

Иногда этот вид погрешности называют неисключенными остатками систематической погрешности (кратко — неисключенные остатки). Например, при измерении длины штрихового метра в длинах волн эталонного излучения выявлено несколько неисключенных систематических погрешностей (_i): из-за неточного измерения температуры — ₁; из-за неточного определения показателя преломления воздуха — ₂, из-за неточного значения длины волны — ₃.

Обычно учитывают сумму неисключенных систематических погрешностей (устанавливают их границы). При числе слагаемых N ≤ 3 границы неисключенных систематических погрешностей вычисляют по формуле

(1.4)

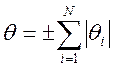
При числе слагаемых N ≥ 4 для вычислений используют формулу

(1.5)

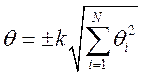
где k — коэффициент зависимости неисключенных систематических погрешностей от выбранной доверительной вероятности Р при их равномерном распределении. При Р = 0,99, k = 1,4, при Р = 0,95, k = 1,1.

Случайная погрешность измерения (кратко — случайная погрешность) — составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) в серии измерений одного и того же размера физической величины. Причины случайных погрешностей: погрешности округления при отсчете показаний, вариация показаний, изменение условий измерений случайного характера и др.

Случайные погрешности вызывают рассеяние результатов измерений в серии.

В основе теории погрешностей лежат два положения, подтверждаемые практикой:

1. При большом числе измерений случайные погрешности одинакового числового значения, но разного знака, встречаются одинаково часто;

2. Большие (по абсолютному значению) погрешности встречаются реже, чем малые.

Из первого положения следует важный для практики вывод: при увеличении числа измерений случайная погрешность результата, полученного из серии измерений, уменьшается, так как сумма погрешностей отдельных измерений данной серии стремится к нулю, т. е.

(1.6)

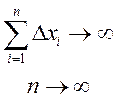
Несмотря на то, что с увеличением числа измерений сумма случайных погрешностей стремится к нулю (в данном примере она случайно получилась равной нулю), обязательно производится оценка случайной погрешности результата измерений. В теории случайных величин характеристикой рассеяния значений случайной величины служит дисперсия 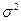о2. «|/о2 = а называют средним квадратическим отклонением генеральной совокупности или стандартным отклонением.

Оно более удобно, чем дисперсия, так как его размерность совпадает с размерностью измеряемой величины (например, значение величины получено в вольтах, среднее квадратическое отклонение тоже будет в вольтах). Так как в практике измерений имеют дело с термином «погрешность», для характеристики ряда измерений следует применять производный от него термин «средняя квадратическая погрешность». Характеристикой ряда измерений может служить средняя арифметическая погрешность или размах результатов измерений.

Размах результатов измерений (кратко — размах) — алгебраическая разность наибольшего и наименьшего результатов отдельных измерений, образующих ряд (или выборку) из n измерений:

где R_n — размах; X_max и Х_min — наибольшее и наименьшее значения величины в данном ряду измерений.

Например, из пяти измерений диаметра d отверстия значения R₅ = 25,56 мм и R₁ = 25,51 мм оказались максимальным и минимальным его значением. В этом случае R_n = d₅ — d₁= 25,56 мм — 25,51 мм = 0,05 мм. Это означает, что остальные погрешности данного ряда менее 0,05 мм.

Средняя арифметическая погрешность отдельного измерения в серии (кратко — средняя арифметическая погрешность) — обобщенная характеристика рассеяния (вследствие случайных причин) отдельных результатов измерений (одной и той же величины), входящих в серию из n равноточных независимых измерений, вычисляется по формуле

(1.8)

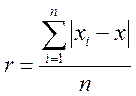
Истинное значение средней арифметической погрешности р определяется из соотношения

При числе измерений n > 30 между средней арифметической (r) и средней квадратической (s) погрешностями существуют соотношения

s = 1,25 r; r и= 0,80 s. (1.10)

Преимущество средней арифметической погрешности — простота ее вычисления. Но все же чаще определяют среднюю квадратическую погрешность.

Средняя квадратическая погрешность отдельного измерения в серии (кратко — средняя квадратическая погрешность) — обобщенная характеристика рассеяния (вследствие случайных причин) отдельных результатов измерений (одной и той же величины), входящих в серию из п равноточных независимых измерений, вычисляемая по формуле

(1.11)

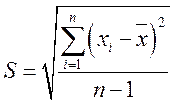
Средняя квадратическая погрешность для генеральной выборки о, являющаяся статистическим пределом S, может быть вычислена при /і-мх > по формуле:

В действительности число измерений всегда ограничено, поэтому вычисляется не σ, а ее приближенное значение (или оценка), которым является s. Чем больше п, тем s ближе к своему пределу σ.

При нормальном законе распределения вероятность того, что погрешность отдельного измерения в серии не превзойдет вычисленную среднюю квадратическую погрешность, невелика: 0,68. Следовательно, в 32 случаях из 100 или 3 случаях из 10 действительная погрешность может быть больше вычисленной.

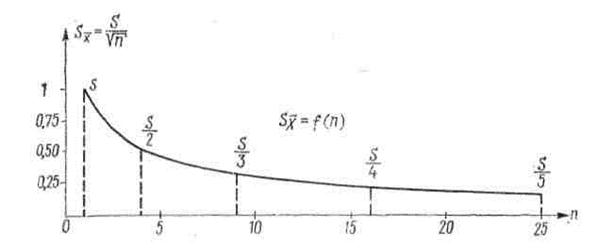Рисунок 1.2 Уменьшение значения случайной погрешности результата многократного измерения при увеличении числа измерений в серии

В серии измерений существует зависимость между средней квадратической погрешностью отдельного измерения s и средней квадратической погрешностью арифметического среднего S_x:

(1.13)

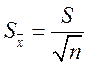
которую нередко называют «правилом У n». Из этого правила следует, что погрешность измерений вследствие действия случайных причин может быть уменьшена в уn раз, если выполнять n измерений одного размера какой-либо величины, а за окончательный результат принимать среднее арифметическое значение (рис. 1.2).

Выполнение не менее 5 измерений в серии дает возможность уменьшить влияние случайных погрешностей более чем в 2 раза. При 10 измерениях влияние случайной погрешности уменьшается в 3 раза. Дальнейшее увеличение числа измерений не всегда экономически целесообразно и, как правило, осуществляется лишь при ответственных измерениях, требующих высокой точности.

Средняя квадратическая погрешность отдельного измерения из ряда однородных двойных измерений S_α вычисляется по формуле

(1.14)

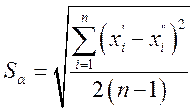
где x’_i и х»_i — і-ые результаты измерений одного размера величины при прямом и обратном направлениях одним средством измерений.

При неравноточных измерениях среднюю квадратическую погрешность арифметического среднего в серии определяют по формуле

(1.15)

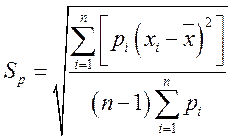
где p_i — вес і-го измерения в серии неравноточных измерений.

Среднюю квадратическую погрешность результата косвенных измерений величины Y, являющейся функцией Y = F (X₁, X₂, X_n), вычисляют по формуле

(1.16)

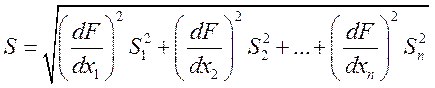
где S₁, S₂, S_n — средние квадратические погрешности результатов измерений величин X₁, X₂, X_n.

Если для большей надежности получения удовлетворительного результата проводят несколько серий измерений, среднюю квадратическую погрешность отдельного измерения из m серий (S_m) находят по формуле

(1.17)

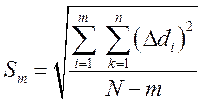
Где n — число измерений в серии; N — общее число измерений во всех сериях; m — число серий.

При ограниченном числе измерений часто необходимо знать погрешность средней квадратической погрешности. Для определения погрешности S, вычисляемой по формуле (2.7), и погрешности S_m, вычисляемой по формуле (2.12), можно воспользоваться следующими выражениями

(1.18)

(1.19)

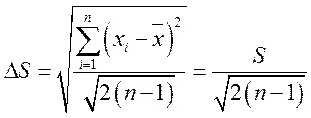
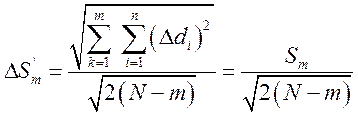
где S и S_m — средние квадратические погрешности соответственно S и S_m.

Например, при обработке результатов ряда измерений длины х получены

= 86 мм 2 при n = 10,

= 3,1 мм

= 0,7 мм или S = ±0,7 мм

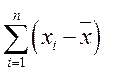
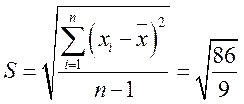
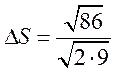
Значение S = ±0,7 мм означает, что из-за погрешности вычисления s находится в пределах от 2,4 до 3,8 мм, следовательно, десятые доли миллиметра здесь ненадежны. В рассмотренном случае надо записать: S = ±3 мм.

Чтобы иметь большую уверенность в оценке погрешности результата измерений, вычисляют доверительную погрешность или доверительные границы погрешности. При нормальном законе распределения доверительные границы погрешности вычисляют как ±t-s или ±t-s_x, где s и s_x — средние квадратические погрешности соответственно отдельного измерения в серии и среднего арифметического; t — число, зависящее от доверительной вероятности Р и числа измерений n.

Важным понятием является надежность результата измерений (α), т.е. вероятность того, что искомое значение измеряемой величины попадет в данный доверительный интервал.

Если 2a = ±3s, то надежность результата a = 0,68, т. е. в 32 случаях из 100 следует ожидать выхода размера детали за допуск 2а. При оценивании качества детали по допуску 2a = ±3s надежность результата составит 0,997. В этом случае можно ожидать выхода за установленный допуск только трех деталей из 1000. Однако увеличение надежности возможно лишь при уменьшении погрешности длины детали. Так, для повышения надежности с a = 0,68 до a = 0,997 погрешность длины детали необходимо уменьшить в три раза.

В последнее время получил широкое распространение термин «достоверность измерений». В некоторых случаях он необоснованно применяется вместо термина «точность измерений». Например, в некоторых источниках можно встретить выражение «установление единства и достоверности измерений в стране». Тогда как правильнее сказать «установление единства и требуемой точности измерений». Достоверность нами рассматривается как качественная характеристика, отражающая близость к нулю случайных погрешностей. Количественно она может быть определена через недостоверность измерений.

Недостоверность измерений (кратко — недостоверность)— оценка несовпадения результатов в серии измерений вследствие влияния суммарного воздействия случайных погрешностей (определяемых статистическими и нестатистическими методами), характеризуемая областью значений, в которой находится истинное значение измеряемой величины.

В соответствии с рекомендациями Международного бюро мер и весов недостоверность выражается в виде суммарной средней квадратической погрешности измерений — Su включающей среднюю квадратическую погрешность S (определяемую статистическими методами) и среднюю квадратическую погрешность u (определяемую нестатистическими методами), т.е.

(1.20)

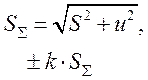
Например, при нормальном законе распределения вероятность появления случайной погрешности, равной ±3s, составляет 0,997, а разность 1-Р = 0,003 незначительна. Поэтому во многих случаях доверительную погрешность ±3s, принимают за предельную, т.е. _пр = ±3s. В случае необходимости _пр может иметь и другие соотношения с s при достаточно большом Р (2s, 2,5s, 4s и т.д.).

В связи с тем, в стандартах ГСИ вместо термина «средняя квадратическая погрешность» применен термин «среднее квадратическое откланение», в дальнейших рассуждениях мы будим придерживаться именно этого термина.

Абсолютная погрешность измерения (кратко — абсолютная погрешность) — погрешность измерения, выраженная в единицах измеряемой величины. Так, погрешность Х измерения длины детали Х, выраженная в микрометрах, представляет собой абсолютную погрешность.

Не следует путать термины «абсолютная погрешность» и «абсолютное значение погрешности», под которым понимают значение погрешности без учета знака. Так, если абсолютная погрешность измерения равна ±2мкВ, то абсолютное значение погрешности будет 0,2 мкВ.

Относительная погрешность измерения (кратко — относительная погрешность) — погрешность измерения, выраженная в долях значения измеряемой величины или в процентах. Относительную погрешность δ находят из отношений:

(1.21)

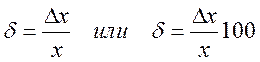
Например, имеется действительное значение длины детали х = 10,00 мм и абсолютное значение погрешности х = 0,01мм. Относительная погрешность составит

Статическая погрешность — погрешность результата измерения, обусловленная условиями статического измерения.

Динамическая погрешность — погрешность результата измерения, обусловленная условиями динамического измерения.

Погрешность воспроизведения единицы — погрешность результата измерений, выполняемых при воспроизведении единицы физической величины. Так, погрешность воспроизведения единицы при помощи государственного эталона указывают в виде ее составляющих: неисключенной систематической погрешности, характеризуемой ее границей ; случайной погрешностью, характеризуемой средним квадратическим отклонением s и нестабильностью за год ν.

Погрешность передачи размера единицы — погрешность результата измерений, выполняемых при передаче размера единицы. В погрешность передачи размера единицы входят неисключенные систематические погрешности и случайные погрешности метода и средств передачи размера единицы (например, компаратора).

Источник