Что называется абсолютной ошибкой
Относительная и абсолютная погрешность – формула определения, как рассчитать погрешность измерения
Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.
Абсолютная погрешность
Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.
Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.
Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:
Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.
На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.
Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.
Относительная погрешность
Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.
Получим число 0,0695, переведем в проценты и получим 6%. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10% и 0,1%. Для отрезка длиной в 10 см погрешность в 1см очень велика, это ошибка в 10%. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1%.
Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.
Правила подсчета погрешностей
Для номинальной оценки погрешностей существует несколько правил:
Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.
Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.
Что мы узнали?
Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.
Приложение А. Погрешности вычислений
Абсолютная и относительная погрешности
Точность полученного в результате вычисления результата определяется погрешностью вычислений. Различают два вида погрешностей – абсолютную и относительную.
Абсолютная погрешность некоторого числа равна разности между его истинным значением и приближенным значением, полученным в результате вычисления или измерения:
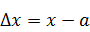
где а – приближенное значение числа х.
Относительная погрешность – это отношение абсолютной погрешности к приближенному значению числа:
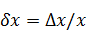
Истинное значение величины х обычно неизвестно. Имеется лишь приближенное значение а и нужно найти его предельную погрешность 

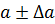
Источники погрешностей
Рассмотрим различные причины возникновения погрешностей.
Математическая модель задачи является неточной
Погрешность возникает из-за того, что сам численный метод или математическая модель является лишь приближением к точному методу (например, дифференцирование). Кроме того, любая математическая модель или метод могут внести существенные погрешности, если в ней не учтены какие-то особенности рассматриваемой задачи. Модель может прекрасно работать в одних условиях и быть совершенно неприемлемой в других. Такую погрешность называют также методической. Она всегда имеет место, даже при абсолютно точных данных и абсолютно точных вычислениях. В большинстве случаев погрешность численного метода можно уменьшить до требуемого значения за счет изменения параметров метода (например, уменьшением шага дискретизации, или увеличением количества итераций).
Ошибки в исходных данных
Исходные данные задачи часто являются основным источником погрешностей. Ошибки такого типа неизбежны и проявляются в любых реальных задачах, поскольку любое измерение может быть проведено с только какой-то предельной точностью. Вместе с погрешностями, вносимыми математической моделью, их называют неустранимыми погрешностями, поскольку они не могут быть уменьшены ни до начала решения задачи, ни в процессе ее решения.
Следует стремиться к тому, чтобы все исходные данные были примерно одинаковой точности. Сильное уточнение одних исходных данных при наличии больших погрешностей в других не приводит к повышению точности конечных результатов. Если какие-то отдельные точки данных (измерения) явно ошибочные, их можно исключить из вычислений.
Вычислительные ошибки (ошибки округления)
Ошибки этого типа проявляются из-за дискретной (а не непрерывной) формы представления величин в компьютере. Вычислительные ошибки можно свести к минимуму продуманно организовывая алгоритмы.
Вычислительные ошибки
Рассмотрим подробнее вычислительные ошибки. Допустим, исходные данные не имеют погрешности, но поскольку место в памяти компьютера, отведенное на хранение чисел, ограничено, и соответственно ограничена точность представления чисел, возникновение вычислительных ошибок неизбежно.
Представление чисел с плавающей точкой
Для хранения целых чисел (int, long, unsigned int и т.д.) обычно отводится 4 байта памяти, что позволяет представлять целые числа, находящиеся примерно в диапазоне от 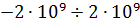
В вычислениях чаще используются вещественные числа (float, double). Такие числа представляются в компьютере в форме с плавающей точкой, и хранятся в логарифмическом виде – мантисса и порядок:
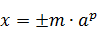
где m – мантисса, p – порядок, а – основание степени.
Например, число 273.9 можно 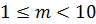
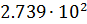
В таблице А.1 приводится диапазон допустимых значений и другие параметры для чисел с плавающей точкой одинарной (float) и двойной (double) точности.
| Точность | Одинарная | Двойная |
| Размер (байты) | 4 | 8 |
| Наименьшее значение | 1.2·10 −38 | 2.3·10 −308 |
| Наибольшее значение | 3.4×10 +38 | 1.7×10 +308 |
| Размеры степени и мантиссы (биты) | 8-23 | 11-52 |
Таблица A.1. Диапазон чисел, представимых в формате с плавающей точкой
Для чисел с плавающей точкой существует понятие машинного эпсилон – наименьшего положительного число ε такого, что 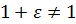
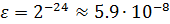
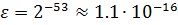
Погрешность округления
При вычислениях с помощью компьютера неизбежны погрешности округлений, связанные с ограниченностью хранимых разрядов мантиссы. Для приближенного числа, полученного в результате округления, абсолютная погрешность 
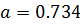
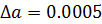
Перевод чисел из одной системы счисления в другую также может быть источником погрешности из-за того, что основание одной системы счисления не является степенью основания другой (например, 10 и 2). Это может привести к тому, что в новой системе счисления число невозможно представить абсолютно точно, например:
Погрешность арифметических действий над приближенными числами
При выполнении операций над приближенными числами можно оценить предельную погрешность результата в зависимости от выполняемой операции. При умножении или делении чисел друг на друга их относительные погрешности складываются:
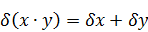
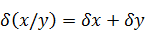
При возведении в степень приближенного числа его относительная погрешность умножается на показатель степени:
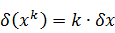
При сложении или вычитании чисел их абсолютные погрешности складываются:
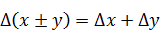
Относительная погрешность суммы положительных слагаемых вычисляется как:
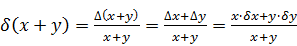
Отсюда следует, что относительная погрешность суммы нескольких чисел одного и того же знака, заключена между наименьшей и наибольшей из относительных погрешностей слагаемых:
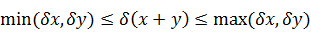
На практике для оценки погрешности при сложении чисел обычно используют максимальную погрешность 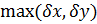
При сложении погрешность будет сильно завесить от абсолютных величин складываемых чисел. Рассмотрим пример сложения двух чисел с одинаковым количеством значащих цифр, но разных по абсолютному значению:
1234 + 0.005678 = 1234.00005678
или в компьютерном представлении:
1.234Е+03 + 5.678Е-03 = 1.234005678Е+03
После сложения количество значащих цифр равно 10. Число с одинарной точностью (float) позволяет хранить только 8 значащих цифр, то есть на самом деле число будет равно 1.2340056Е+03. Две значащие цифры потерялись в процессе сложения. Потеря точности здесь возникает из-за того, что при прибавлении к большому числу малых чисел результат сложения выходит за пределы точности при округлении. Для того чтобы уменьшить погрешность вычислений, нужно складывать числа в порядке возрастания их абсолютной величины. Таким образом можно минимизировать абсолютную величину промежуточной погрешности при каждом сложении.
Рассмотрим теперь вычитание чисел (сложение чисел разного знака, или вычитание чисел одного знака). В соответствии с выражением (А.7) относительная погрешность может быть очень большой в случае, если числа близки между собой, так как даже при малых погрешностях 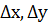
Таким образом, можно сделать вывод, что сложение и вычисление являются плохо обусловленными (неустойчивыми) операторами, так как при некоторых данных даже небольшая погрешность в исходных данных может привести к большой погрешности результата. Уменьшить погрешность можно за счет правильной последовательности операций. Из-за погрешности округления в машинной арифметике важен порядок выполнения операций, и известные из алгебры законы коммутативности (и дистрибутивности) здесь не всегда выполняются.
Измерения. Классификация ошибок измерений
В физике и в других науках весьма часто приходится производить измерения различных величин (например, длины, массы, времени, температуры, электрического сопротивления и т. д.).
Измерение – процесс нахождения значения физической величины с помощью специальных технических средств – измерительных приборов.
Измерительным прибором называют устройство, с помощью которого осуществляется сравнение измеряемой величины с физической величиной того же рода, принятой за единицу измерения.
Различают прямые и косвенные методы измерений.
Прямые методы измерений – методы, при которых значения определяемых величин находятся непосредственным сравнением измеряемого объекта с единицей измерения (эталоном). Например, измеряемая линейкой длина какого-либо тела сравнивается с единицей длины – метром, измеряемая весами масса тела сравнивается с единицей массы – килограммом и т. д. Таким образом, в результате прямого измерения определяемая величина получается сразу, непосредственно.
Косвенные методы измерений – методы, при которых значения определяемых величин вычисляются по результатам прямых измерений других величин, с которыми они связаны известной функциональной зависимостью. Например, определение длины окружности по результатам измерения диаметра или определение объема тела по результатам измерения его линейных размеров.
Ввиду несовершенства измерительных приборов, наших органов чувств, влияния внешних воздействий на измерительную аппаратуру и объект измерения, а также прочих факторов все измерения можно производить только с известной степенью точности; поэтому результаты измерений дают не истинное значение измеряемой величины, а лишь приближенное. Если, например, вес тела определен с точностью до 0,1 мг, то это значит, что найденный вес отличается от истинного веса тела менее чем на 0,1 мг.
Точность измерений – характеристика качества измерений, отражающая близость результатов измерений к истинному значению измеряемой величины.
Чем меньше погрешности измерений, тем больше точность измерений. Точность измерений зависит от используемых при измерениях прибо- ров и от общих методов измерений. Совершенно бесполезно стремиться при измерениях в данных условиях перейти за этот предел точности. Можно свести к минимуму воздействие причин, уменьшающих точность измерений, но полностью избавиться от них невозможно, то есть при измерениях всегда совершаются более или менее значительные ошибки (погрешности). Для увеличения точности окончательного результата всякое физическое измерение необходимо делать не один, а несколько раз при одинаковых условиях опыта.
Абсолютная и относительная погрешности



Абсолютной погрешностью измерения называется величина, определяемая разницей между результатом измерения x и истинным значением измеряемой величины x0:
Величина δ, равная отношению абсолютной погрешности измерения к результату измерения, называется относительной погрешностью:
δ =
Пример 2.1. Приближённым значением числа π является 3.14. Тогда погрешность его равна 0.00159. Абсолютную погрешность можно считать равной 0.0016, а относительную погрешность равной 0.0016/3.14 = 0.00051 = 0.051 %.
Например, число 0.0283 имеет три верных значащих цифры, а 2.5400 – пять верных значащих цифр.
Правила округления чисел. Если приближённое число содержит лишние (или неверные) знаки, то его следует округлить. При округлении возникает дополнительная погрешность, не превышающая половины единицы разряда последней значащей цифры (d) округлённого числа. При округлении сохраняются только верные знаки; лишние знаки отбрасываются, причём если первая отбрасываемая цифра больше или равна d/2, то последняя сохраняемая цифра увеличивается на единицу.
Лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются (как и лишние нули). Например, если погрешность измерения 0.001 мм, то результат 1.07005 округляется до 1.070. Если первая из изменяемых нулями и отбрасываемых цифр меньше 5, остающиеся цифры не изменяются. Например, число 148935 с точностью измерения 50 имеет округление 148900. Если первая из заменяемых нулями или отбрасываемых цифр равна 5, а за ней не следует никаких цифр или идут нули, то округление производится до ближайшего чётного числа. Например, число 123.50 округляется до 124. Если первая из заменяемых нулями или отбрасываемых цифр больше 5 или равна 5, но за ней следует значащая цифра, то последняя остающаяся цифра увеличивается на единицу. Например, число 6783.6 округляется до 6784.
Пример 2.2. При округлении числа 1284 до 1300 абсолютная погрешность составляет 1300 – 1284 = 16, а при округлении до 1280 абсолютная погрешность составляет 1280 – 1284 = 4.
Пример 2.3. При округлении числа 197 до 200 абсолютная погрешность составляет 200 – 197 = 3. Относительная погрешность равна 3/197 ≈ 0.01523 или приближённо 3/200 ≈ 1.5 %.
Пример 2.4. Продавец взвешивает арбуз на чашечных весах. В наборе гирь наименьшая – 50 г. Взвешивание дало 3600 г. Это число – приближённое. Точный вес арбуза неизвестен. Но абсолютная погрешность не превышает 50 г. Относительная погрешность не превышает 50/3600 = 1.4 %.
Погрешности решения задачи на PC
В качестве основных источников погрешности обычно рассматривают три вида ошибок. Это так называемые ошибки усечения, ошибки округления и ошибки распространения. Например, при использовании итерационных методов поиска корней нелинейных уравнений результаты являются приближёнными в отличие от прямых методов, дающих точное решение.
Ошибки усечения
Этот вид ошибок связан с погрешностью, заложенной в самой задаче. Он может быть обусловлен неточностью определения исходных данных. Например, если в условии задачи заданы какие-либо размеры, то на практике для реальных объектов эти размеры известны всегда с некоторой точностью. То же самое касается любых других физических параметров. Сюда же можно отнести неточность расчётных формул и входящих в них числовых коэффициентов.
Ошибки распространения
Данный вид ошибок связан с применением того или иного способа решения задачи. В ходе вычислений неизбежно происходит накопление или, иначе говоря, распространение ошибки. Помимо того, что сами исходные данные не являются точными, новая погрешность возникает при их перемножении, сложении и т. п. Накопление ошибки зависит от характера и количества арифметических действий, используемых в расчёте.
Ошибки округления
Это тип ошибок связан с тем, что истинное значение числа не всегда точно сохраняется компьютером. При сохранении вещественного числа в памяти компьютера оно записывается в виде мантиссы и порядка примерно так же, как отображается число на калькуляторе.
Относительная погрешность
Погре́шность измере́ния — оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.
Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного. (Это отклонение принято называть ошибкой измерения. В ряде источников, например, в БСЭ, термины ошибка измерения и погрешность измерения используются как синонимы.) Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. При этом за истинное значение принимается среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T=2.8±0.1 c. означает, что истинное значение величины T лежит в интервале от 2.7 с. до 2.9 с. некоторой оговоренной вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка).
В 2006 году на международном уровне был принят новый документ, диктующий условия проведения измерений и установивший новые правила сличения государственных эталонов. Понятие «погрешность» стало устаревать, вместо него было введено понятие «неопределенность измерений».
Содержание
Определение погрешности
В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы.
Классификация погрешностей
По форме представления
где Xtrue — истинное значение, а Xmeas — измеренное значение, должно выполняться с некоторой вероятностью близкой к 1. Если случайная величина Xmeas распределена по нормальному закону, то, обычно, за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.

Относительная погрешность является безразмерной величиной, либо измеряется в процентах.
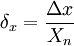
— если шкала прибора односторонняя, т.е. нижний предел измерений равен нулю, то Xn определяется равным верхнему пределу измерений;
— если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.
По причине возникновения
В технике применяют приборы для измерения лишь с определенной заранее заданной точностью – основной погрешностью, допускаемой нормали в нормальных условиях эксплуатации для данного прибора.
Если прибор работает в условиях, отличных от нормальных, то возникает дополнительная погрешность, увеличивающая общую погрешность прибора. К дополнительным погрешностям относятся: температурная, вызванная отклонением температуры окружающей среды от нормальной, установочная, обусловленная отклонением положения прибора от нормального рабочего положения, и т.п. За нормальную температуру окружающего воздуха принимают 20°С, за нормальное атмосферное давление 01,325 кПа.