Что находится внутри квадрата загадка
Загадки на тему «Геометрия»
Сколько граней у шестигранного карандаша?
Загадка для детей №4015.
Загадка для детей №4107.
Загадка для детей №4075.
Загадка для детей №4040.
Загадка для детей №4071.
Загадка в рифму №3796.
Загадка для детей №3801.
Не похож я на пятак,
Не похож на рублик.
Круглый я, да не дурак,
С дыркой, но не бублик.
Загадка в рифму №3800.
Эта форма у клубка,
У планеты, колобка,
Но сожми ее, дружок,
И получится …
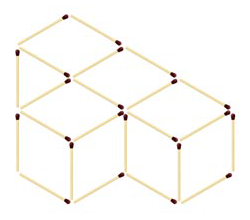
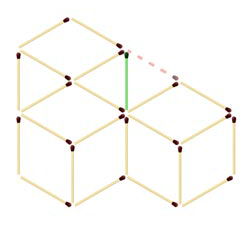
Есть куб — черный снаружи, но белый внутри. Высота его равна его ширине и толщине и составляет три локтя.
Задания:
1. Сколько разрезов понадобится, чтобы разделить большой куб на маленькие кубики размером всего в один локоть?
2. Сколько получится кубиков после такого разрезания?
3. Сколько из кубиков будут с 4 черными гранями, сколько — с 3, с 2 и с одной только черной гранью?
4. Сколько всего получится маленьких черных граней и сколько получится кубиков, совершенно белых со всех сторон?
Что находится внутри квадрата загадка
Следующая загадка
PS. А Тельце-то свой хреновенький метод на практике сама опробовала.
Источник: опыт, сын ошибок трудных
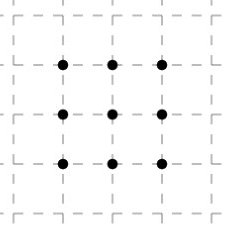
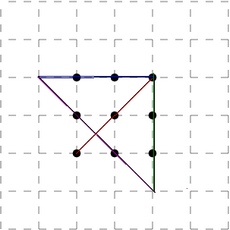
сверху вниз, потом по диагонали вверх и вправо, потом влево, вниз по диагонали вправо и влево. вот и все!
сто пудов никак, либо одна сторона не прорисованная, либо одна сторона 2 раза прочерчена.
А девушке Тельце кол, сами попробуйте нарисовать то, что написали )))
Элементарно. Только крест надо рисовать не двумя черточками.
КОНЕЧНО МОЖНО. В ЛАГЕРЕ ДЕТСКОМ ЕЩЁ ТАК ВСЕХ НА ВКУСНЯХИ РАЗВОДИЛ. ДА И ЩА РАБОТАЕТ. Я ЗНАЮ КАК.
Следующая загадка
Почему пред ним все приклоняются. Лучший ответ
Обычно Кааба покрыта черным шелковым покрывалом. Верхнюю часть покрывала украшают вышитые золотом изречения из Корана, которые украшают и покрывало, закрывающее дверь в Каабу. Дверь эта, возвышающаяся над землей примерно на 2 м, сделана из чистого золота и весит 286 кг. Во время посещения и очищения внутренности Каабы к двери приставляют лестницу. Внутри находятся три колонны, висят многочисленные лампы, расписанные эмалью, хранятся дарственные списки Корана.
Каабу окружает мощеная дорожка, по которой паломники совершают ритуальные обходы святилища…
Остальные ответы этот храм построили пророки Авраам и Исмаел (мир им) Сергей ЛогутовМастер (1524) 11 лет назад Но что внутри. Hakan Shukur Просветленный (20912) камень есть но только мы не приклоняемся))) Сергей ЛогутовМастер (1524) 11 лет назад Извини если неправильно написал. Hakan Shukur Просветленный (20912) да все нормально ))))))) кусок черного камня (метеорита) по слухам вмурован в стену Каабы.
Когда храм был почти готов, Ибрахиму понадобился заметный камень, чтобы обозначить на стене место, с которого следует начинать ритуальное обхождение вокруг Каабы. Дело в том, что в раю ангелы и Адам, наученные самим Богом, совершали семикратное обхождение вокруг храма, и Ибрахим хотел, чтобы и на земле богослужение происходило правильно. Тут-то ангел Джибрил и принес ему знаменитый Черный камень, который был вделан в северо-восточный угол здания, — этот камень первоначально был ослепительной белизны, но затем быстро почернел от прикосновений грешников.
Следующая загадка
Эту головоломку не смогли разгадать знатоки клуба «Что? Где? Когда?». Хотя, когда вы узнаете решение, вы поймете, что головоломка очень легкая.
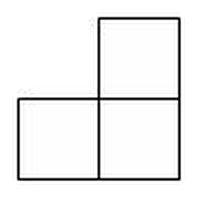
Вот как звучит задание: «Перед тобой — шесть фигур, расположенных в определенной последовательности. Внимание, вопрос! Какая фигура (которой нет в этом ряду) должна быть в начале этого ряда?»
Под катом правильный ответ:
А может вы сначала напишите комментарий, догадались или нет, если догадались, то какая фигура должна быть вначале. Потом уже смотрите правильный ответ.
[ ВОТ ТУТ ПРАВИЛЬНЫЙ ОТВЕТ ]
А ведь все очень просто! Надо лишь совсем чуть-чуть подумать. Загадочные символы на картинке — это последовательность цифр от 2 до 7 — в реальном виде и в зеркальном отражении: 2, 3, 4, 5, 6, 7.
Так что правильный ответ — М! В данном случае это не совсем буква, а цифра 1 в естественном обличье и ее зеркальный двойник.
Загадки про квадрат для детей
Где может попасться такая геометрическая фигура, как квадрат? В принципе, абсолютно везде в повседневной жизни. Если хорошенько подумать, то на Гладстон попадается достаточно часто: строительные конструкции, элементы одежды.
Ознакомившись с нашими загадками про квадрат для детей можно неплохо расширить собственный кругозор и узнать о том, какие роли ещё может встретиться данный объект. Не просто отличный способ весело провести время с ребёнком, но ещё и достаточно поучительный.
У меня угла четыре
И четыре стороны.
Все они между собою
Одинаково равны.
Не овал я и не круг,
Треугольнику я друг,
Прямоугольнику я брат,
Ведь зовут меня…
Четырёхугольник я.
У сторон – одна длина.
Все углы мои прямые.
Догадайся, кто же я?
Фигура в геометрии мила,
Внутри четыре прямых угла,
Четыре линии в фигурной окантовке,
Равны в размерах, сопрягаясь ловко!
Четыре угла и четыре сторонки,
Похожи точно родные сестренки.
В ворота его не закатишь, как мяч,
И он за тобою не пустится вскачь.
Фигура знакома для многих ребят.
Его вы узнали? Ведь это …
Он давно знакомый мой,
Каждый угол в нем прямой,
Все четыре стороны
Одинаковой длины.
Вам его представить рад.
А зовут его…
Кубик в краску окуни,
Приложи и подними.
Если ты уже так сделал –
Отпечатались они.
Красив и строг: ведь у него
Равны все стороны его.
Сложен словно на парад.
Что же это? Да.
Если стороны равны
И углы его прямы,
А сторон, углов четыре,
Что с тобой мы начертили?
Если шесть мы их возьмём,
Сможем куб собрать.
Только помни: надо шесть,
А совсем не пять.
Смотреть на ту фигуру радостно,
Углы в три сотни с лишним градусов,
Все стороны всегда, к примеру,
Изумительно равных размеров!
Я фигура – хоть куда,
Очень ровная всегда,
Все углы во мне равны
И четыре стороны.
Кубик – мой любимый брат,
Потому что я…
Загадки про прямоугольник Загадки прямоугольник
Данная подборка включает в себя 20 загадок про прямоугольник для детей. В текстах детских загадок про эту геометрическую фигуру часто упоминается углы, равные стороны и что прямоугольник похож на квадрат. Такие головоломки будут по душе дошкольникам и школьникам (1-2 класс). Загадки про прямоугольник можно задавать и на уроках, чтобы разнообразить обучение.
Солнце светит нам в окно,
И на нашем на ковре
Есть четыре стороны,
Попарно стороны равны.
На нее похожи очень
Дверь, окно и кошелёчек.
Мой холст – не квадратный,
Точно также угловат,
Статью не обижен
Он, как брат его – квадрат,
Только ростом ниже.
Дверь в стене и книжный шкаф,
Даже книжка на руках,
И окно, и подоконник –
Если сложишь два квадрата,
То его получишь ты.
Та фигура длинновата,
Сквозь него мы входим в дом
На него кирпич похож.
И нам он очень нужен.
У него углы прямые
Те, которые напротив,
Параллельны и равны.
Обведи кирпич мелком
На асфальте целиком,
И получится фигура –
Ты, конечно, с ней знаком.
Он похож на дверь, на книжки,
И на ранец у мальчишки,
На окно, на подоконник.
Вы подумайте, скажите.
Только помнить вы должны:
Стороны фигуры этой
С виду он ну очень прост,
Его построить – не вопрос,
И он совсем не виноват,
Что вдвое больше, чем квадрат.
На квадрат он хоть похож,
Но отличия есть всё ж.
Лишь попарные равны.
А с углами всё в порядке:
Все углы его прямы.
Как-то раз мой младший брат
Начертил большой квадрат.
А к нему – еще один
Сбоку он присоединил.
И вот этот вот угольник
Как автобус, как тетрадка,
Как большая шоколадка.
Как корыто поросенка
И как фантик у ребенка.
Не квадрат, не треугольник,
Растянули мы квадрат
И представили на взгляд,
На кого он стал похожим
Или с чем-то очень схожим?
Не кирпич, не треугольник –
Фото папы, фото мамы
И для этих фото рамы.
Нарисуем мы подряд
Раз квадрат и два квадрат
И получим сразу непростой угольник.
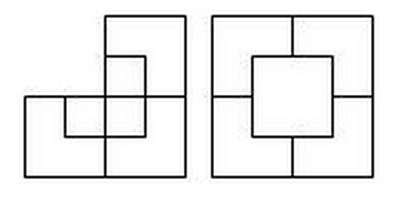
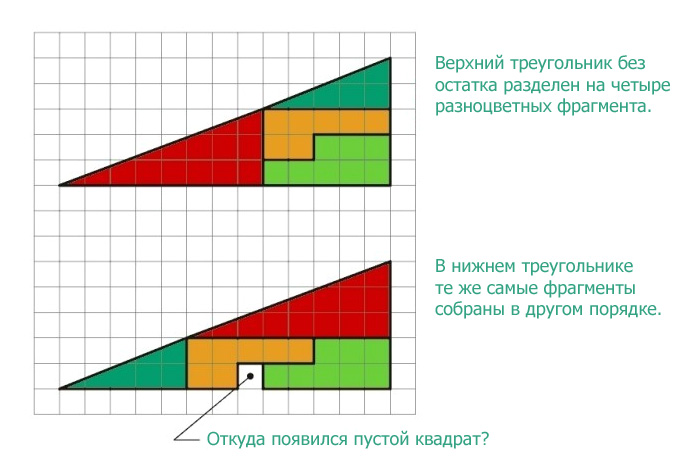
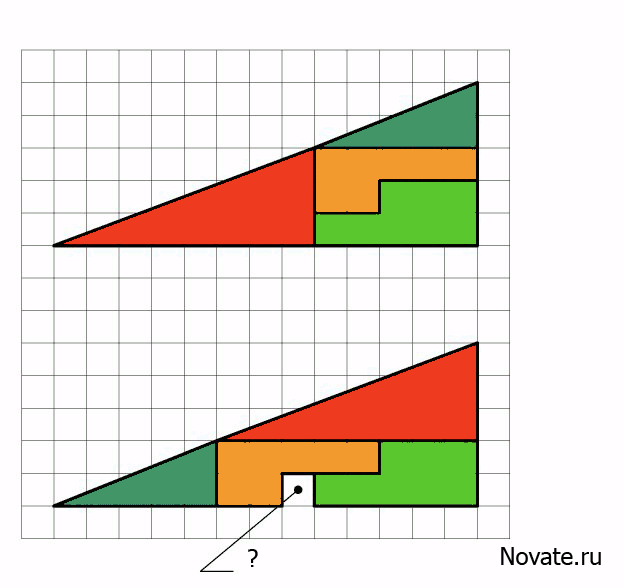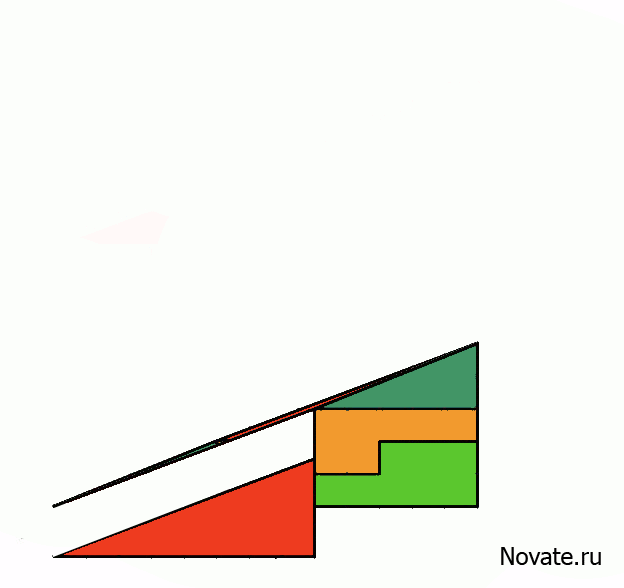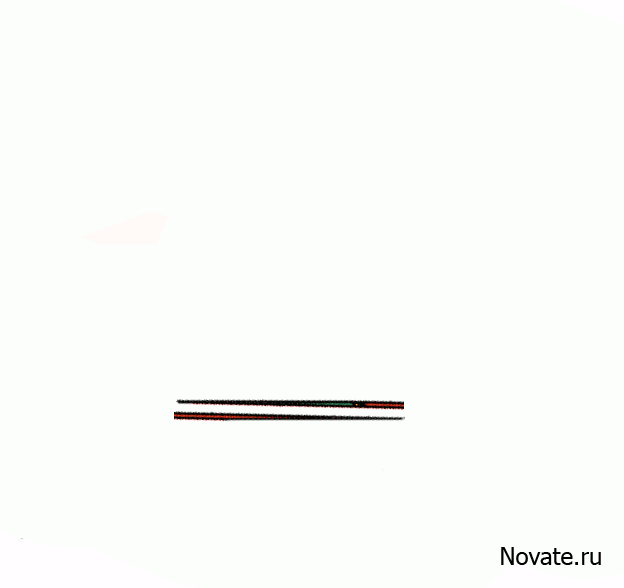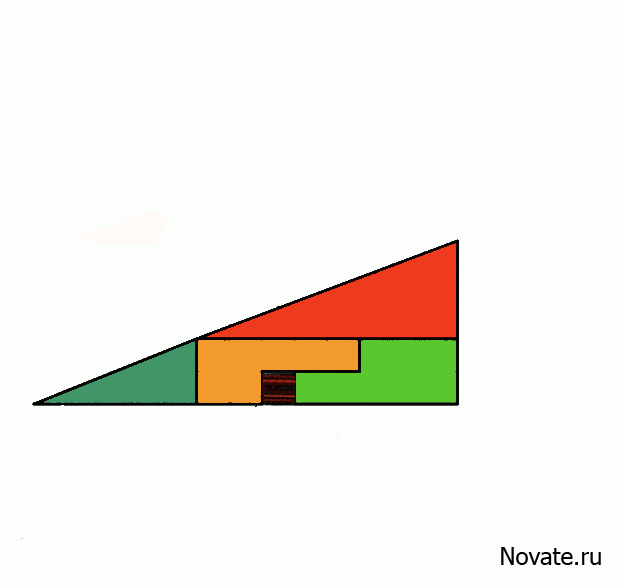
Задачка на сообразительность: откуда появился лишний пустой квадрат
Получайте на почту один раз в сутки одну самую читаемую статью. Присоединяйтесь к нам в Facebook и ВКонтакте.
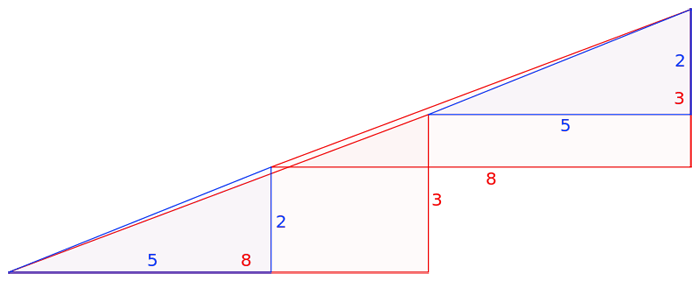
В действительности это не оптический обман, а интересная задача. Площади закрашенных фигур, разумеется, равны между собой (32 клетки), однако, то, что визуально наблюдается как треугольники 13×5, на самом деле таковым не является, и имеет разные площади (S13×5 = 32,5 клетки). То есть ошибка, замаскированная в условии задачи, состоит в том, что начальная фигура поименована треугольником (на самом деле это — вогнутый 4-угольник). Это отчётливо заметно на рисунке-схеме ниже — «гипотенузы» верхней и нижней фигур проходят через разные точки: (8,3) вверху и (5,2) — внизу. Секрет в свойствах синего и красного треугольников. Это легко проверить вычислениями.
Отношения длин соответствующих сторон синего и красного треугольников не равны друг другу (2/3 и 5/8), поэтому эти треугольники не являются подобными, а значит, имеют разные углы при соответствующих вершинах. Назовём первую фигуру, являющуюся вогнутым четырёхугольником, и вторую фигуру, являющуюся вогнутым восьмиугольником, псевдотреугольниками. Если нижние стороны этих псевдотреугольников параллельны, то гипотенузы в обоих псевдотреугольниках 13×5 на самом деле являются ломаными линиями (на верхнем рисунке создаётся излом внутрь, а на нижнем — наружу). Если наложить верхнюю и нижнюю фигуры 13×5 друг на друга, то между их «гипотенузами» образуется параллелограмм, в котором и содержится «лишняя» площадь. На рисунке-схеме этот параллелограмм приведён в верных пропорциях.
Острый угол в этом параллелограмме равен arcctg 46 ≈ 0°1′18,2″. На такой угол минутная стрелка на исправных часах сдвигается за 12,45 с. Именно на такую величину тупой угол в рассматриваемом параллелограмме отличается от развёрнутого. Визуально столь ничтожное отличие незаметно, зато оно хорошо просматривается на анимации.
По словам Мартина Гарднера, эту задачу изобрёл иллюзионист-любитель из Нью-Йорка Пол Карри в 1953. Однако принцип, заложенный в неё, был известен ещё в 1860-е годы. Можно заметить, что длины сторон фигур из данной задачи (2, 3, 5, 8, 13) являются последовательными числами Фибоначчи.
Понравилась статья? Тогда поддержи нас, жми: