Что находится поперек ординаты
Ордината
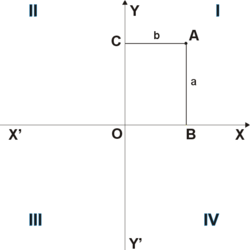
Ординатой (от лат. ordinatus — расположенный в порядке) точки A называется координата этой точки на оси Y’Y в прямоугольной системе координат. Величина ординаты точки A равна длине отрезка OC (см. рис. 1). Если точка C принадлежит положительной полуоси OY, то ордината имеет положительное значение. Если точка C принадлежит отрицательной полуоси Y’O, то ордината имеет отрицательное значение. Если точка A лежит на оси X’X, то её ордината равна нулю.
В прямоугольной системе координат ось Y’Y называется «осью ординат».
См. также
Смотреть что такое «Ордината» в других словарях:
Ордината — Когда данные изображаются в виде графика, ордината соответствует информации, содержащейся на вертикальной оси, или оси «У». При экспериментальных исследованиях на этой оси размещаются значения зависимой переменной. Психология. А Я. Словарь… … Большая психологическая энциклопедия
ОРДИНАТА — (от лат. ordinatus расположенный в порядке) одна из декартовых координат точки, обычно вторая, обозначаемая буквой y … Большой Энциклопедический словарь
ОРДИНАТА — ОРДИНАТА, ординаты, жен. (лат. ordinata расположенная на равных расстояниях) (мат.). В системе координат аналитической геометрии перпендикуляр на плоскости, опущенный из точки на ось абсцисс. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ордината — сущ., кол во синонимов: 1 • координата (4) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
ордината — Разность долгот начала и конца профиля, измеренная на данной широте [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN ordinatedeparture … Справочник технического переводчика
ордината — В картографии координата, отсчитываемая по направлению, перпендикулярному осевому меридиану … Словарь по географии
ОРДИНАТА — одно из двух (трёх) чисел, определяющих положение точки на плоскости (в пространстве) относительно прямоугольной системы координат … Большая политехническая энциклопедия
ордината — (лат. ordinatus упорядоченный, расставленный в известном порядке) ееом. одно из двух (трех) чисел, определяющих положение точки на плоскости (в пространстве) относительно прямоугольной системы координат. Новый словарь иностранных слов. by EdwART … Словарь иностранных слов русского языка
ордината — ы; ж. [от лат. ordinatus упорядоченный, назначенный] Матем. Величина, определяющая положение некоторой точки на плоскости или в пространстве по оси Y в прямоугольной системе координат (ср. абсцисса, ордината). * * * ордината (от лат. ordinatus … … Энциклопедический словарь
ордината — ordinatė statusas T sritis fizika atitikmenys: angl. ordinate vok. Ordinate, f rus. ордината, f pranc. ordonnée, f … Fizikos terminų žodynas
Активный туризм на Юге России
1.10. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ НА КАРТАХ
Рис. 14. Прямоугольные координаты
В топографии и геодезии, а также на топографических картах ориентирование производится по северу со счетом углов по ходу часовой стрелки, поэтому для сохранения знаков тригонометрических функций положение осей координат, принятое в математике, повернуто на 90°.
Прямоугольные координаты на топографических картах СССР применяются по координатным зонам. Координатные зоны — части земной поверхности, ограниченные меридианами с долготой, кратной 6°. Первая зона ограничена меридианами 0° и 6°, вторая—б» и 12°, третья—12° и 18° и т.д.
Счет зон идет от Гринвичского меридиана с запада на восток. Территория СССР располагается в 29 зонах: от 4-й до 32-й включительно. Протяженность каждой зоны с севера на юг порядка 20000 км. Ширина зоны на экваторе около 670 км, на широте 40°— 510 км, т широте 50°—430 км, на широте 60°—340 км.
Все топографические карты в пределах данной зоны имеют общую систему прямоугольных координат. Началом координат в каждой зоне служит точка пересечения среднего (осевого) меридиана зоны с экватором (рис. 15), средний меридиан зоны соответствует
Рис. 15. Система прямоугольных координат на топографических картах: а—одной зоны; б—части зоны
Зависимость между условными координатами и их действительными значениями выражается формулами:
X ‘ = Х-, У = У— 500 000,
Х = 5 650 450: Y = 3 620 840,
то это значит, что точка расположена в третьей зоне на удалении 120 км 840 м от среднего меридиана зоны (620840—500000) и к северу от экватора на удалении 5650 км 450 м.
Полные координаты — прямоугольные координаты, записанные (названные) полностью, без каких-либо сокращений. В примере, приведенном выше, даны полные координаты объекта:
Х = 5 650 450; Y = 3620 840.
Сокращенные координаты применяются для ускорения целеука-зания по топографической карте, в этом случае указываются только десятки и единицы километров и метры. Например, сокращенные координаты данного объекта будут:
Х = 50 450; Y = 20 840.
Сокращенные координаты нельзя применять при целеуказании на стыке координатных зон и если район действий охватывает пространство протяженностью более 100 км по широте или долготе.
Координатная (километровая) сетка —сетка квадратов на топографических картах, образованная горизонтальными и вертикальными линиями, проведенными параллельно осям прямоугольных координат через определенные интервалы (табл. 5). Эти линии называются километровыми. Координатная сетка предназначается для определения координат объектов и нанесения на карту объек тов по их координатам, для целеуказания, ориентирования карты, измерения дирекционных углов и для приближенного определения расстояний и площадей.
Как найти координаты точки?
3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие системы координат
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
Определение координат точки
Каждой точке координатной плоскости соответствуют две координаты.
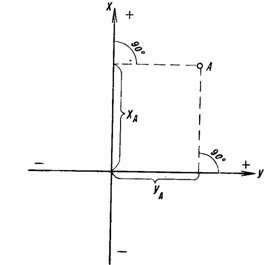
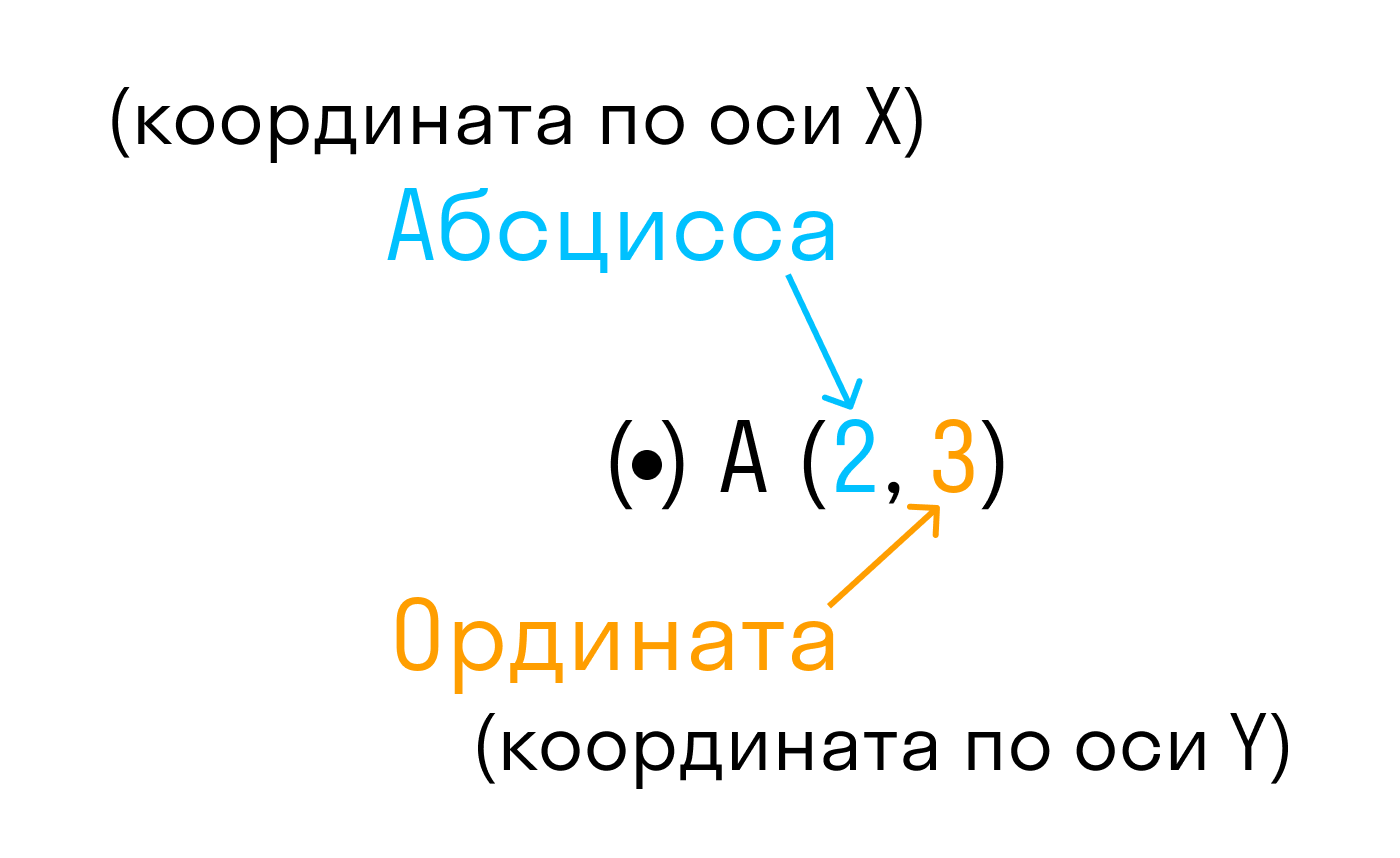
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.
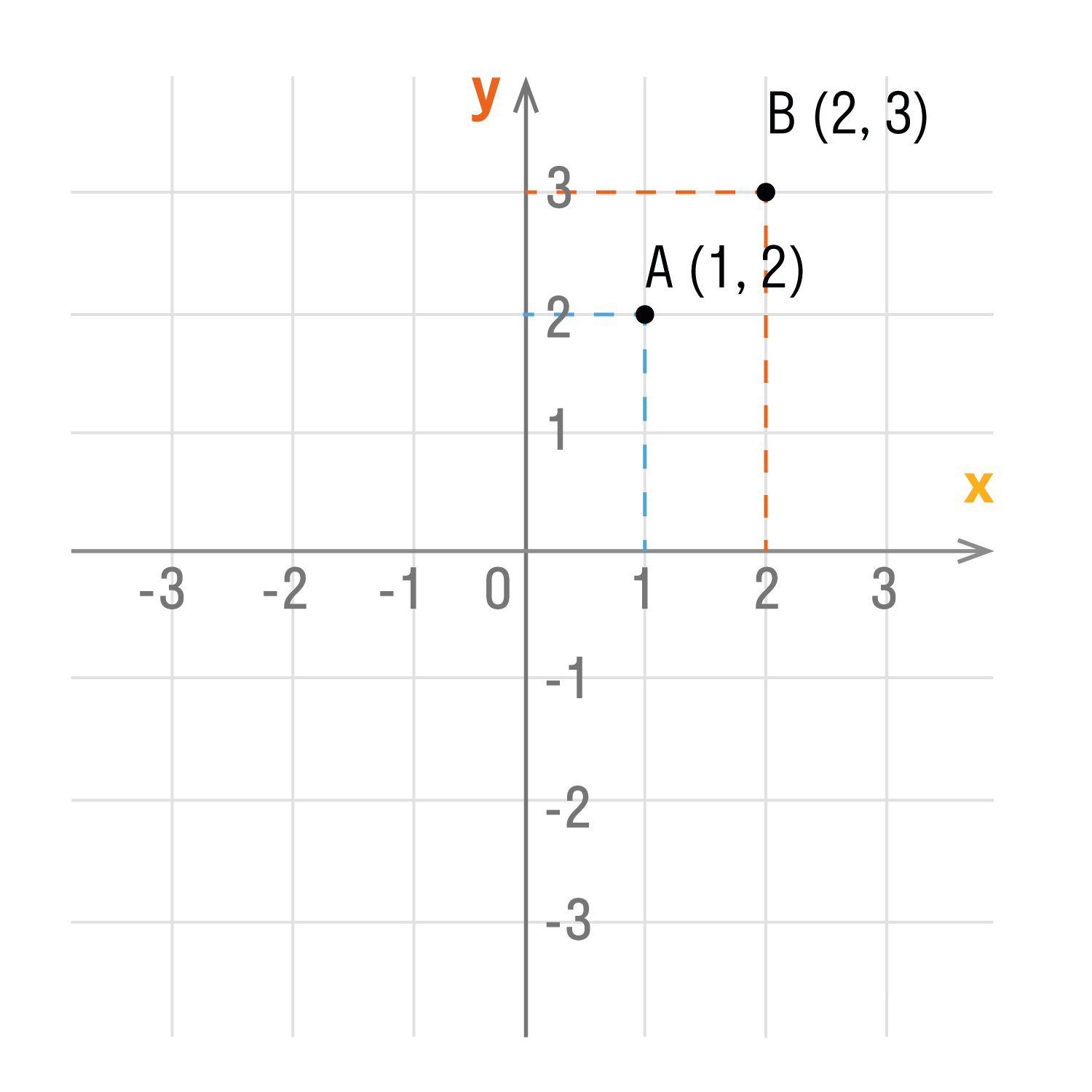
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.
Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.
Смотрим на график и фиксируем: A (1; 2) и B (2; 3).
Особые случаи расположения точек
В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:
Способы нахождения точки по её координатам
Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.
Способ первый. Как определить положение точки D по её координатам (-4, 2):
Способ второй. Как определить положение точки D (-4, 2):
Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:
График линейной функции, его свойства и формулы
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
Понятие линейной функции
Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Для удобства результаты можно оформлять в виде таблицы:
Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».
| Функция | Коэффициент «k» | Коэффициент «b» |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».
Еще не устали? Изучать математику веселее с опытным преподавателем на курсах по математике в Skysmart!
Свойства линейной функции
Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1 /3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.
В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).
В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.
Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).
Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.
При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.
Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.
Если k 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Точки пересечения графика функции y = kx + b с осями координат:
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Квадратичная функция. Построение параболы
8 класс, 9 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.
Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.
Построение квадратичной функции
Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:
График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.
График функции y = –x 2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
Рассмотрим три случая:
Если a > 0, то график выглядит как-то так:
0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>
На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.
Как строим:
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
Как строим:
Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
Рассмотрим следующий пример: y = (x − 2) × (x + 1).
Как строим:
Данный вид уравнения позволяет быстро найти нули функции:
(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.
Определим координаты вершины параболы:
Найти точку пересечения с осью OY:
с = ab = (−2) × (1) = −2 и ей симметричная.
Отметим эти точки на координатной плоскости и соединим плавной прямой.