Что мы знаем о вертикальных углах

Вертикальные углы

Какие углы вертикальные? Каким свойством обладают вертикальные углы?

Рассмотрим определение вертикальных углов и их свойство, а также применим свойство вертикальных углов для решения задач.

Определение.

Вертикальные углы — это пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.

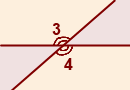
При пересечении двух прямых образуется две пары вертикальных углов:

∠1 и ∠2 — вертикальные углы

∠3 и ∠4 — вертикальные углы

Свойство вертикальных углов.

Вертикальные углы равны.

Таким образом, при пересечении двух прямых образуется две пары равных межу собой углов.

1) Сумма вертикальных углов равна 140º. Найти эти углы.

Так как вертикальные углы равны, а в условии сказано, что их сумма равна 140º, то каждый из них равен по 140:2=70º.

2) Сумма двух углов, образованных при пересечении двух прямых, равна 100º. Найти эти углы.

При пересечении двух прямых образуются углы двух видов — вертикальные и смежные.

Так как сумма смежных углов равна 180º, а по условию, сумма углов равна 100º, то эти углы — вертикальные.

А так как вертикальные углы равны, то каждый из них равен по 100:2=50º.

Вертикальные углы во многих задачах — важный элемент при доказательстве равенства треугольников и подобия треугольников.

Источник

Смежные и вертикальные углы

Смежные углы

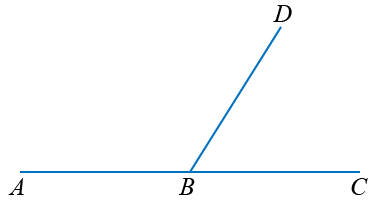
Смежные углы — это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Следовательно, два смежных угла составляют развёрнутый угол. Общая сторона двух смежных углов называется наклонной к прямой, на которой лежат другие стороны (только в том случае, когда смежные углы не равны).

∠ABD и ∠DBC — это смежные углы, AC — прямая, луч BD — общая сторона углов и наклонная к прямой AC, ∠ABC — развёрнутый угол, B — основание наклонной.

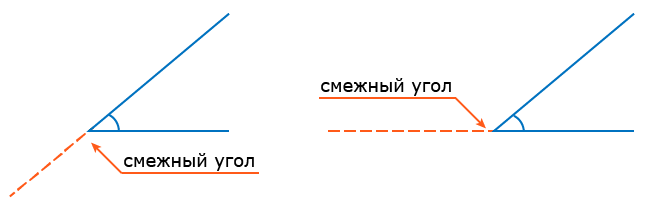
Чтобы построить угол, смежный с данным углом, нужно одну из сторон угла продлить за вершину:

Сумма смежных углов

Любые два смежных угла составляют в сумме развёрнутый угол. Развёрнутый угол равен двум прямым углам, поэтому можно сказать, что сумма двух смежных углов равна двум прямым углам.

где d — это обозначение прямого угла (d = 90°).

Вертикальные углы

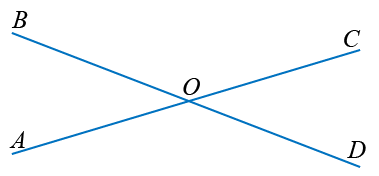
Вертикальные углы — это пара углов, у которых стороны одного угла являются продолжением сторон другого угла. Пересечение двух прямых линий образует две пары вертикальных углов:

∠AOB и ∠COD, а также ∠AOD и ∠BOC — вертикальные углы.

Равенство вертикальных углов

Вертикальные углы равны между собой. Рассмотрим вертикальные углы 1 и 3:

Сумма ∠1 и ∠2 равна развёрнутому углу (180°). Сумма ∠2 и ∠3 тоже равна развёрнутому углу (180°). Значит:

Следовательно, ∠1 = ∠3. Равенство вертикальных углов доказано.

Источник

Вертикальные углы. 7-й класс

Разделы: Математика

Класс: 7

Цель урока:

Образовательная: формирование знаний о вертикальных углах, умения самостоятельно определять вертикальные углы в комбинациях геометрических фигур, умения применять знания при решении геометрических задач и способов деятельности;

Развивающая: формирование умений анализировать, устанавливать причинно-следственные связи, развитие умения сравнивать и находить различий и сходства у смежных и вертикальных углов, развитие умение обобщать и синтезировать знания о смежных и вертикальных углах, развитие умения выдвигать гипотезы и предположения, развитие ассоциативного мышления, воображения;

Воспитательная: воспитание личностных качеств, обеспечивающих успешность исполнительской деятельности, воспитание активности, увлеченности, целеустремленности, наблюдательности, интуиции, сообразительности, самостоятельности.

Оборудование: компьютер, интерактивная доска, карточки-смайлики, карточки-опросники для рефлексии;

Приемы и методы ведения урока: проблемная ситуация, диалоговое общение, объяснение, эвристическая беседа, презентация.

Ход урока

Цель: вовлечение учащихся в учебный процессОрганизует положительный настрой на урок, вспоминает с учащимися способы деятельности

Добрый день. Начинаем наш урок. С каким настроением вы приступаете к работе?

— Прежде чем выяснить, чего мы не знаем, что необходимо сделать?Воспринимают информацию, реагируют на вопросы учителя.

Учащиеся дают ответ с помощью сигнальных карточек-смайликов

-Надо выяснить, чего мы не знаем и самостоятельно найти выход из затруднения.

-Выяснить, что нам известно.Включение учащихся в учебную деятельность, формирование познавательных УУД2.Актуализаци опорных знаний. Мотивация учебной деятельности учащихся

Цель: активизация мотивационной деятельностиИнформирует о новых знаниях, мотивирует учебную деятельность:

— В какой большой теме мы с вами сейчас работаем?

— Вспомните план, по которому идет изучение любой темы?

— Что из перечисленного мы уже изучили?

Сформулируйте свойство смежных углов.Воспринимают информацию, обнаруживают первичное понимание:

Определение угла, смежные углы, дают определения, вспоминают свойство смежных углов.Развитие коммуникативных компетенций, коммуникативных УУД3.Актуализация знаний

Цель: подготовка к усвоению новых знанийСлайд 1

Ребята, а что можно сказать об углах 4 и 2, 1 и 3, 5 и 7?Учащиеся на основании определения смежных углов находят пары смежных углов

Учащиеся предполагают, что они равны, что стороны одного являются дополнительными полупрямыми к сторонам другого, возможно среди предполагаемых названий пар возникнет название “вертикальные”Осознание потребности к построению нового способа действий.4.Первичное усвоение новых знаний

Цель: восприятие учащимися и первичное осознание нового учебного материалаОрганизует первичное усвоение знаний учащимися

Как они выглядят, какое название им можно дать?

Тема сегодняшнего урока:

Цель нашего урока: познакомиться с понятием вертикальных углов, их свойством и научиться решать задачи с применением этих свойств.

Два угла называются вертикальными, если стороны одного являются дополнительными полупрямыми сторон другого

Что можно сказать о вертикальных углах, каким свойством они обладают?

Верно! Давайте докажем это. Итак, теорема: Вертикальные углы равны.

Пусть 1 и 2 – данные вертикальные углы, СОD и DOA. Отсюда, по теореме о сумме смежных углов заключаем, что каждый из углов DOC и AOB дополняет угол AOD до 180 градусов, т.е. 1 = 2. Что и требовалось доказать.

Давайте найдем, где в учебнике рассказано о вертикальных углах и их свойствах, откройте стр. 22 учебника, п.15. Найдите определение вертикальных углов. Прочитайте. Найдите Теорему о вертикальных углах, прочитайте.Осмысливают, углубляют понимание нового материала

Учащиеся записывают дату, тему урока в тетрадь

Учащиеся переносят рисунок в тетрадь, наносят обозначения

Учащиеся выдвигают гипотезу, что вертикальные углы равны

Учащиеся записывают краткую запись теоремы: если 1 и 2 вертикальные, то 1 = 2

Учащиеся записывают доказательство.

Учащиеся работают с учебником, читают вслух определение вертикальных углов и теорему о вертикальных углах.Усвоение нового понятия “вертикальные углы”, и новых способов деятельности, развитие регулятивной компетенции5. Первичная проверка понимания

Цель: становление правильности и осознанности усвоения нового учебного материала; выявление пробелов и неверных представлений и их коррекцияОрганизует проверку понимания на примере нестандартной ситуации

А теперь, ребята, найдем вертикальные углы в нестандартных ситуациях, внимание на интерактивную доску:

На основании чего можно сделать такой вывод?Демонстрируют первичное понимание полученных знаний:

Учащиеся определяют пары вертикальных углов: 6 и 4,

3 и 5 и объясняют почему они вертикальные.

DFM и BFA, DFB и MFA,Усвоение понятия вертикальных углов и их свойств, формирование критического мышления6.Первичное закрепление

Цель: выявление пробелов, неверных представлений и их коррекцияОрганизует решением задач

А теперь рассмотрим следующую задачу:

— Какие углы изображены на чертеже?

— Сколько пар вертикальных углов вы видите?

— Чтобы найти углы 1 и 2 какие свойства нужно применить?

Приступим к решению:

DOA и AOB являются смежными, т.к. АО – общая, а DO и OB – дополнительные полупрямые. Значит, по свойству смежных углов:

Решим ещё одну задачу. Откройте учебник, стр.26, задача №7.

Учитель делает чертеж на доске:

Какие углы при этом образуются?

Повторим свойства смежных и вертикальных углов.

Учащиеся записывают условие задачи, делают чертёж, наносят обозначения.

— свойства смежных углов, свойства вертикальных углов, формулируют эти свойства;

К доске выходит 1 ученик и решает задачу совместно с классом под руководством учителя. Учащиеся записывают решение в тетрадь.

Учащиеся работают с учебником. Читают задачу вслух: Один из углов, которые получаются при пересечении двух прямых, равен 30 градусов. Чему равны остальные углы?

Две пересекающиеся прямые.

Острые, тупые, вертикальные, смежные.

Учащиеся озвучивают свойства смежных и вертикальных углов. Один из учащихся идет к доске для решения задачи.Применение свойств вертикальных углов при решении задач, формирование способности к обобщению, развитие умения работать с текстом7.Информация о домашнем задании, инструктаж по его выполнению

Цель: обеспечение понимания цели, содержания и способов выполнения домашнего заданияЗакройте тетради, откройте дневники, запишите домашнее задание:

Откройте учебники, найдите номера домашнего задания.

№9. Прочитайте вслух условие

Какие углы могут образовываться при пересечении двух прямых?

№10. Прочитайте вслух условие

Какие углы могут образовываться при пересечении двух прямых?

Может ли один из вертикальных углов быть в 4 раза больше другого? Каким свойством нужно воспользоваться в задаче?

№11. Прочитайте вслух условие

Какие углы могут образовываться при пересечении двух прямых?

Может ли один из вертикальных углов быть в на 50 градусов меньше другого?

Каким свойством нужно воспользоваться в задаче?Учащиеся закрывают тетради.

Открывают дневники, записывают д/з.

Открывают учебники, стр.27

Свойством вертикальных и смежных углов

Учащиеся читают вслух условие: Один из углов, образованных при пересечении двух прямых, в четыре раза больше другого. Найдите эти углы.

Свойством вертикальных и смежных углов

Учащиеся читают вслух условие: Один из углов, образованных при пересечении двух прямых, на 50 градусов меньше другого. Найдите эти углы.

Свойством вертикальных и смежных угловОсмысление приемов и способов деятельности8.Рефлексия

Цель: выявление уровня осознания содержания пройденного— Выполнили вы сегодня условия учебной деятельности?

— Какую цель ставили перед собой на уроке?

— Смогли ли ее достичь?

— Выполнили ли основную задачу урока?

— Что более всего понравилось на уроке?

Напиши, над чем тебе надо еще поработать дома и на следующем уроке.

— Оцените свое настроение на сегодняшнем уроке. (Оценка происходит с помощью карточек—смайликов )

— Спасибо вам большое! Вы хорошо поработали на уроке. Урок окончен.Ученики отвечают на вопросы фронтально.

Оценивают свою деятельность с помощью карточки самооценки.

Источник

Угол. Свойства смежных и вертикальных углов.

Сумма двух смежных углов равна двум прямым углам.

Даны два смежных угла: АОВ и ВОС. Требуется доказать, что:

Восставим из точки О к прямой АС перпендикуляр OD. Мы разделили угол АОВ на две части AOD и DOB так, что можно написать:

Прибавим к обеим частям этого равенства по одному и тому же углу BOС, отчего равенство не нарушится:

что и требовалось доказать.

Следствия.

Если из одной точки ( O) прямой (AB) восстановить к ней, по каждую ее сторону, перпендикуляры, то эти перпендикуляры образуют одну прямую (СD). Из всякой точки вне прямой можно опустить на эту прямую перпендикуляр и притом только один.

Потому, что сумма углов COB и BOD равна 2d.

Прямая С части которой OС и OD служат перпендикулярами к прямой AB, называется прямой перпендикулярной к AB.

Если прямая СD перпендикулярна к прямой AB, то и наоборот: AB перпендикулярна к СD, потому что части OA и OB служат также перпендикулярны к СD. Поэтому прямые AB и СD называются взаимноперпендикулярными.

То, что две прямые AB и СD взаимноперпендикулярны, выражают письменно так AB ^ СD.

Два угла называются вертикальными, если стороны одного составляют продолжение сторон другого.

Два вертикальных угла равны.

Пусть даны два вертикальных угла: AOD и СOB т.е. OB есть продолжение OA, а OС продолжение OD.

По свойству смежных углов можем написать:

Значит: AOD + DOB = DOB + BOС.

Если вычесть из обеих частей этого равенства по углу DOB, получим:

Источник

Основы геодезии

О геодезии и разный полезный материал для геодезистов.

Измерение вертикальных углов

Вертикальный угол – это плоский угол, лежащий в вертикальной плоскости. К вертикальным углам относятся угол наклона и зенитное расстояние. Угол между горизонтальной плоскостью и направлением линии местности называется углом наклона и обозначается буквой ν. Углы наклона бывают положительные и отрицательные.

Угол между вертикальным направлением и направлением линии местности называется зенитным расстоянием и обозначается буквой Z. Зенитные расстояния всегда положительные (рис.4.20).

Угол наклона и зенитное расстояние одного направления связаны соотношением:

Вертикальный круг теодолита. Вертикальный круг теодолита предназначен для измерения вертикальных углов, то-есть, углов наклона или зенитных расстояний.

Вертикальный круг большинства теодолитов устроен следующим образом: лимб вертикального круга жестко соединен с трубой (насажен на один из концов оси трубы), центр лимба совмещен с геометрической осью вращения трубы, а его плоскость перпендикулярна этой оси. Деления на лимбе наносят по разному: либо от 0 до 360, либо от 0 до 180 в обе стороны со знаками “плюс” и “минус” или без знаков и т.д. Для отсчета по лимбу имеется алидада. Основные части алидады: отсчетное приспособление, цилиндрический уровень (или компенсатор) и микрометренный винт.

Пузырек уровня в момент отсчета приводится в нуль-пункт, то есть, ось уровня служит указателем горизонтального направления. Отсчетным индексом является нулевой штрих отсчетного приспособления. Ось уровня и линия отсчетного индекса (линия, соединяющая отсчетный индекс с центром лимба) должны быть параллельны; при выполнении этого условия линия отсчетного индекса будет горизонтальна в момент взятия отсчета по вертикальному кругу.

Взаимное положение лимба и зрительной трубы должно удовлетворять условию: визирная линия трубы и нулевой диаметр лимба должны быть параллельны.

Оба условия вместе составляют так называемое главное условие вертикального круга теодолита; оно читается так: визирная линия трубы должна занимать горизонтальное положение, когда отсчет по лимбу равен нулю и пузырек уровня находится в нульпункте. На практике оба эти условия могут не выполняться и имеет место случай, изображенный на рис.4.21-а.

Во-первых, при насаживании лимба на ось трубы между нулевым диаметром лимба и визирной линией трубы остается малый угол x. Во-вторых, линия отсчетного индекса может быть непараллельна оси уровня и между ними существует малый угол y. Таким образом, хотя отсчет по лимбу равен нулю, визирная линия трубы занимает наклонное положение, и угол наклона ее равен:

Если установить визирную линию горизонтально (рис.4.21-б), то отсчет по лимбу станет равным:

Этот отсчет называется местом нуля вертикального круга и обозначается М0.

Таким образом, место нуля вертикального круга теодолита – это отсчет по лимбу вертикального круга при горизонтальном положении визирной линии трубы и оси уровня вертикального круга.

Для конкретного теодолита формулы для вычисления угла наклона и места нуля приводятся в паспорте. Например, для теодолитов 2Т30 и Т15 эти формулы имеют вид:

Положение вертикального круга, при котором отсчет по лимбу вертикального круга равен (с точностью до M0) углу наклона, считается основным; у большинства современных теодолитов основным положением является КЛ.

Для измерения углов наклона удобно иметь М0 близким к нулю, поэтому нужно регулярно выполнять поверку места нуля, которая предусматривает следующие действия:

наведение трубы на точку при КЛ, приведение пузырька уровня в нульпункт и взятие отсчета по вертикальному кругу,
перевод трубы через зенит, наведение трубы на точку при КП, приведение пузырька уровня в нульпункт и взятие отсчета по вертикальному кругу,
вычисление по соответствующим формулам места нуля М0 и угла наклона ν.

Если М0 получается большим, то при основном положении круга нужно навести трубу на точку и микрометренным винтом алидады установить отсчет, равный углу наклона; при этом пузырек уровня отклонится от нульпункта. Исправительными винтами уровня привести пузырек в нульпункт.

Источник