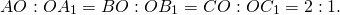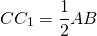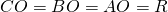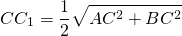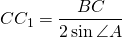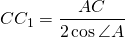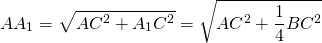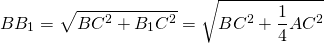Что мы знаем о медиане прямоугольного треугольника

Медиана в прямоугольном треугольнике

Медиана в прямоугольном треугольнике — это отрезок, который соединяет вершину треугольника и середину противоположной стороны, то есть вершину острого угла с серединой противолежащего катета или вершину прямого угла с серединой гипотенузы.

Все медианы прямоугольного треугольника пересекаются в одной точке и делятся этой точкой в отношении два к одному, считая от вершины:

Из всех медиан прямоугольного треугольника в задачах чаще всего речь идет о медиане, проведенной к гипотенузе. Это связано с ее свойствами.

Свойства медианы, проведенной к гипотенузе:

1) Медиана, проведенная к гипотенузе, равна половине гипотенузы.

(в следующий раз рассмотрим доказательство этого свойства)

2) Медиана, проведенная к гипотенузе, равна радиусу описанной около прямоугольного треугольника окружности.

Пользуясь свойствами прямоугольного треугольника, длины медиан прямоугольного треугольника можно выразить через катеты и острые углы.

Например:

12 Comments

Информация очень хорошая. Правда не помогла мне решить задачу, которую мой сын не решил на контрольной. приведу условие:
Из прямого угла треугольника проведена медиана на гипотенузу. Длина медианы 6см. Определить катеты.

Петр, данных для определения катетов недостаточно. Длина гипотенузы в 2 раза больше длины медианы — 12 см. Это всё, что можно сказать по данным условия.

не правда надо провести высоту из прямого угла дальше все получится. один катет равен 6 а второй 2 корня из 22

Сумма квадратов катетов равна квадрату гипотенузы. Проверим 6^2+(2*корень из 22)^2
=36+4*22=36+88=124. Квадрат гипотенузы 12^2=144

попробуйте составить уравнение,обозначив 1 из катетов через х а 2-ой катет обозначьте буквами…x^2+BC^2=12^2…да числа не очень,но это 1 способ..решаю дальше:BC^2=12^2-x^2
BC^2=11x
X^2+11X=144
X^2=12
x(1 катет)=корню из 12,а «-ой катет=11 корней из 12….решал на основе теоремы пифагора

задача имеет бесконечное кол-во решений. решение возможно только в виде формулы или графика, где описана зависимость между катетами и гипотенузой

Да просто треугольник медианой делится на два треугольника с одинаковыми катетами, а дальше как уже предлагалось выше Пифагор во спасение))

А кто вам сказал, что медиана в прямоугольном треугольнике является еще и высотой? Откуда у вас два треугольника с одинаковыми катетами?

Спасибо за понятное объяснение, но у нас задача немного другая.
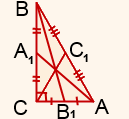
В прямоугольном треугольнике АВС угол С= 90 градусов,медиана ВВ1 равна 10 см.Найдите медианы АА1 СС1, если известно, что АС=12 см.( используя т.Пифагора.

1) Рассмотрим треугольник BB1C. В нём угол С равен 90 градусов, BB1=10 см, B1C=6 см (так как BB1 — медиана). По теореме Пифагора находим BC: BC=8 см. 2) Рассмотрим треугольник AA1C. В нём угол С равен 90 градусов, AC=12 см, AA1=4 см (так как BB1 — медиана). По теореме Пифагора находим AA1: AA1=4√10 см.3) Из треугольника ABC по теореме Пифагора найдём AB: AB=4√13 см. 4) CC1=1/2 AB (как медиана, проведённая к гипотенузе), CC1=2√13 см.
Где-то так.

Источник

Элементы треугольника. Медиана

Определение

Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны

Свойства

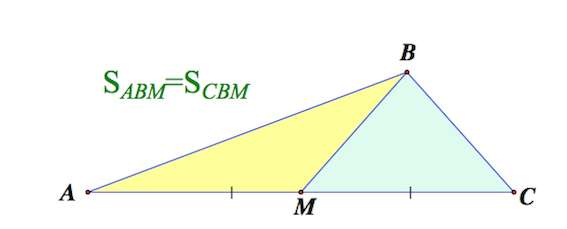
2. Медиана треугольника делит его на два треугольника равной площади (равновеликих треугольника)

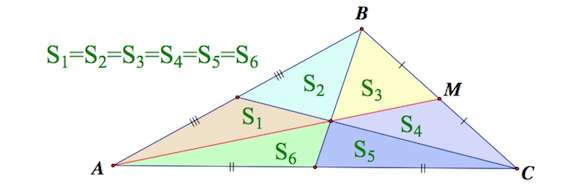
3. Медианы треугольника делят треугольник на 6 равновеликих треугольников

4. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы

5. Длина медианы треугольника вычисляется по формуле:

, где где — медиана к стороне ; — стороны треугольника

6. Длина стороны треугольника через медианы вычисляется по формуле:

, где – медианы к соответствующим сторонам треугольника, — стороны треугольника.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Источник

Всё о медиане

Медиана — это золотое сечение треугольника

Поговорим о таком понятии в математике, как МЕДИАНА.

У этого слова несколько значений, и обо всех мы упомянем. Но в первую очередь нас интересует то, с которым знакомят школьников на уроках геометрии ближе к старшим классам.

И в этом случае МЕДИАНА имеет непосредственное отношение к такой геометрической фигуре, как треугольник.

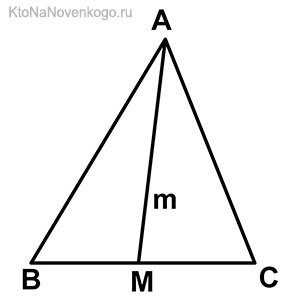
Медиана – это отрезок или часть прямой линии, которая проведена из вершины треугольника к середине противоположной стороны. Точно так же называется и длина этого отрезка.

Вот обратите внимание на этот простой, но очень наглядный рисунок. На нем изображен треугольник со сторонами АВ, АС и ВС, или как принято писать в математике — треугольник АВС.

Точка М – это середина стороны ВС. И соответственно линия АМ, проведенная из вершины А до середины стороны ВС, и есть МЕДИАНА.

Стоит отметить, что сам термин имеет латинский корень. И в переводе дословно означает «средний». А чтобы еще проще было запомнить, что такое медиана, есть прекрасный стишок:

Есть в треугольнике обычном Отрезок очень непростой Соединяет он обычно с серединой стороны любой И каждый должен знать отлично, Зовется медианой он.

Кстати, если внимательно прочитать это стихотворение, то в нем можно выделить ключевые слова – «с серединой стороны ЛЮБОЙ». То есть в нашем примере медиана может выходить не только из вершины А, но также из В и С. И делить пополам не только сторону ВС, но и АС и АВ соответственно.

И выглядят они вот так.

На этом рисунке мы отчетливо видим все три медианы. Они обозначаются отрезками CA, PL и KM.

Пересечение медиан треугольника

Точка О, в которой пересекаются все медианы треугольника, также имеет свое особое название. И даже несколько – центр тяжести, центроид, геометрический центр, барицентр, центр инерции. Ну а неформально эту точку называют точкой равновесия.

Чтобы лучше понять, что это такое, представьте себе треугольник, вырезанный из бумаги или картона. Если вы на нем проведете все три медианы и найдете точку их пересечения, то подставив под нее палец, вы сможете удерживать ваш картонный треугольник в равновесии, не давая ему упасть.

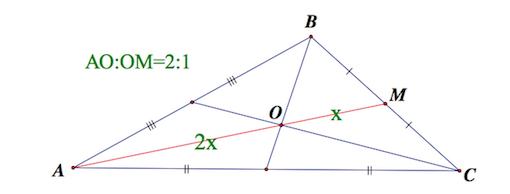
Важно! С точкой пересечения медиан связан один математический факт. Она делит каждую медиану на два отрезка, соотношение которых составляет 2 к 1, если считать от вершины.

Если для примера взять указанный выше треугольник, то тогда это правило можно расписать следующим образом:

Это правило не требует доказательств. Но если хотите, можете провести в домашних условиях опыт и убедиться в правдивости расчетов.

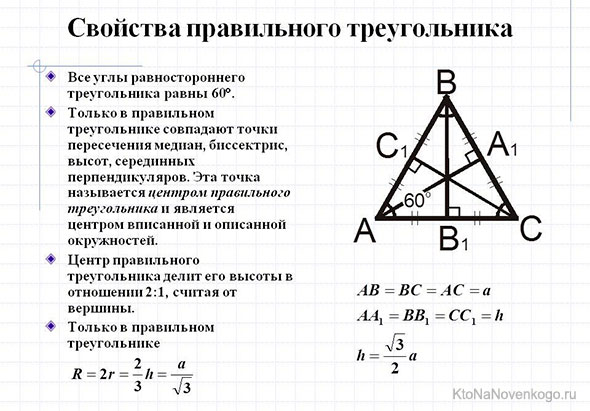
Медиана равностороннего треугольника

Равносторонний треугольник сам по себе уникален, так как все его три стороны имеют одинаковую длину. Логично предположить, что и медиана в нем какая-то особенная?! Да, так оно и есть.

Медиана в равностороннем треугольнике является одновременно и высотой, и биссектрисой.

И наконец, еще одна «фишка» равностороннего треугольника. У него все три медианы равны по длине.

Кстати, присмотритесь к рисунку. С помощью медиан в любом треугольнике образуются внутренние маленькие треугольники. Так вот, в равносторонней фигуре они равны между собой как по длине сторон, так и по площади.

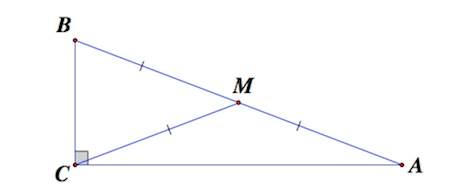
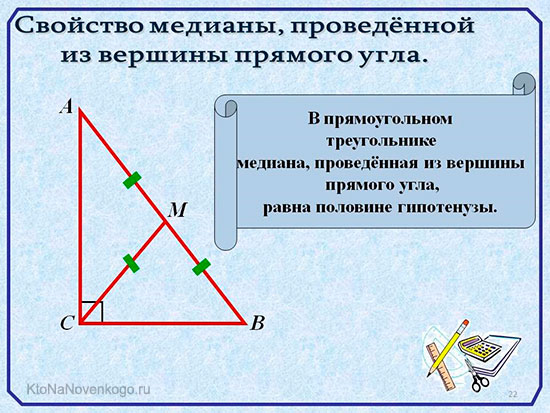
Медиана прямоугольного треугольника

Прямоугольный треугольник, если кто забыл, это треугольник, у которого один угол составляет 90 градусов. И в такой фигуре медиана тоже обладает уникальными свойствами.

Но речь идет только о той медиане, которая выходит из прямого угла. Так вот, ее длина равна половине длины гипотенузы. Так называют самую длинную сторону прямоугольного треугольника.

Соответственно, при решении задач правдиво будет и обратное условие. Так, если указано, что отрезок СМ в нашем примере равен АВ/2, или равен отдельно АМ и ВМ, то можно смело делать вывод, что перед нами прямоугольный треугольник.

А теперь вернемся к тому, о чем мы говорили в самом начале статьи. Термин МЕДИАНА имеет несколько значений.

Например, а в статистике медианой называют уровень показателей, который делит все данные на две равные половины.

Слово «медиана» используется и в дорожном строительстве, обозначая середину асфальтного полотна. Правда, этот термин можно найти только в технических документациях, а в обычной жизни мы говорим просто «разделительная полоса».

И наконец, в Сербии есть археологический памятник, который называется Медиана. Так назвалась древнеримская вилла, руины которой находятся в городе Неш. Она уникальна тем, что была построена при императоре Константине в 300 году и была его резиденцией, в которой он принимал почетных гостей.

Источник

Определение и свойства медианы треугольника

В данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала.

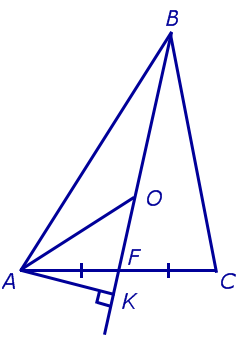
Определение медианы треугольника

Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.

Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).

Свойства медианы

Свойство 1 (основное)

Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.

В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:

Свойство 2

Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.

Свойство 3

Три медианы делят треугольник на 6 равновеликих треугольников.

Свойство 4

Наименьшая медиана соответствует большей стороне треугольника, и наоборот.

Свойство 5

Допустим, известны все стороны треугольника (примем их за a, b и c).

Длину медианы m_a, проведенную к стороне a, можно найти по формуле:

Примеры задач

Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.

Решение
Воспользуемся формулой, приведенной в свойстве 5:

Источник

Каким свойством обладает медиана прямоугольного треугольника

В этой статье мы рассмотрим свойства медианы в прямоугольном треугольнике, а также их доказательства.

Медиана — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. Для прямоугольного треугольника это будут медианы, проведённые с острого угла к серединам катетов или с прямого к центру гипотенузы (рис. 1).

Свойства медианы в прямоугольном треугольнике

Доказательства свойств

Первое свойство

Доказать, что медианы в прямоугольном треугольнике пересекаются в одной точке и делятся в пропорции 2:1, считая от вершины.

Доказательство:

Что и требовалось доказать.

Второе свойство

Доказать, что медиана, проведённая с вершины прямого угла к гипотенузе, равна половине гипотенузы.

Доказательство:

Что и требовалось доказать.

Третье свойство

Доказать, что медиана, проведённая к гипотенузе прямоугольного треугольника, является радиусом описанной окружности.

Доказательство:

Что и требовалось доказать.

У этого термина существуют и другие значения, см. Медиана.

Треугольник и его медианы.

Медиа́на треуго́льника (лат. mediāna — средняя) ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Иногда медианой называют также прямую, содержащую этот отрезок. Точка пересечения медианы со стороной треугольника называется основанием медианы.

Связанные определения[править | править код]

Три медианы, проходящие через общую точку

На рис. справа в треугольнике ABC через точку O проведены 3 медианы: AD, BE и CF. Тогда точка O пересечения 3 медиан разбивает каждую медиану на 2 отрезка прямых, один из них (который начинается в вершине, а заканчивается в точке пересечения O) мы назовем домедианой или предмедианой, а второй из них (который начинается в точке пересечения O, а заканчивается в точке его пересечения со стороной, противоположной вершине) мы назовем постмедианой.[1]
С помощью этих 2 понятий совсем просто формулируются некоторые теоремы геометрии. Например, в любом треугольнике отношение пред- и постмедианы равно двум.

Свойства[править | править код]

Основное свойство[править | править код]

Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

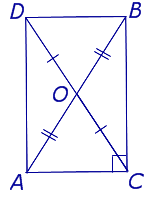
Свойства медиан равнобедренного треугольника[править | править код]

В равнобедренном треугольнике две медианы, проведенные к равным сторонам треугольника, равны, а третья медиана одновременно является биссектрисой и высотой. Верно и обратное: если в треугольнике две медианы равны, то треугольник — равнобедренный, а третья медиана одновременно является биссектрисой и высотой угла при своей вершине.

У равностороннего треугольника все три медианы равны.

Свойства оснований медиан[править | править код]

Другие свойства[править | править код]

Бесконечно удаленная прямая — трилинейная поляра центроида

Основные соотношения[править | править код]

Чтобы вычислить длину медианы, когда известны длины сторон треугольника, применяется теорема Аполлония (выводится через теорему Стюарта или достроением до параллелограмма и использованием равенства в параллелограмме суммы квадратов сторон и суммы квадратов диагоналей):

где — медианы к сторонам треугольника соответственно.

В частности, сумма квадратов медиан произвольного треугольника составляет 3/4 от суммы квадратов его сторон:

Обратно, можно выразить длину произвольной стороны треугольника через медианы:

где — медианы к соответствующим сторонам треугольника, — стороны треугольника.

Площадь любого треугольника, выраженная через длины его медиан:

где — полусумма длин медиан.

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Примечание. В данном уроке изложены теоретические материалы и решение задач по геометрии на тему “медиана в прямоугольном треугольнике”. Если Вам необходимо решить задачу по геометрии, которой здесь нет – пишите об этом в форуме. Почти наверняка курс будет дополнен.

Определение медианы

Медианой треугольника называется отрезок, соединяющий один из углов треугольника с серединой противолежащей ему стороны.

(медианой также называют прямую, содержащую данный отрезок)

Задачи по геометрии, предлагаемые для решения, в основном, используют следующие свойства медианы прямоугольного треугольника.

Обозначения в формулах:

a, b – катеты прямоугольного треугольника

c – гипотенуза прямоугольного треугольника

Если обозначить треугольник, как ABC, то

(то есть стороны a,b,c – являются противолежащими соответствующим углам)

ma– медиана, проведенная к катету а

mb – медиана, проведенная к катету b

mc – медиана прямоугольного треугольника, проведенная к гипотенузе с

α (альфа) – угол CAB, противолежащий стороне а

Задача про медиану в прямоугольном треугольнике

Медианы прямоугольного треугольника, проведенные к катетам, равны, соответственно, 3 см и 4 см. Найдите гипотенузу треугольника

Решение

Прежде чем начать решение задачи, обратим внимание на соотношение длины гипотенузы прямоугольного треугольника и медианы, которая опущена на нее. Для этого обратимся к формулам 2, 4, 5 свойств медианы в прямоугольном треугольнике. В этих формулах явно указано соотношение гипотенузы и медианы, которая на нее опущена как 1 к 2. Поэтому,для удобства будущих вычислений (что никак не повлияет на правильность решения, но сделает его более удобным), обозначим длины катетов AC и BC через переменные x и y как 2x и 2y (а не x и y).

Рассмотрим прямоугольный треугольник ADC. Угол C у него прямой по условию задачи, катет AC – общий с треугольником ABC, а катет CD равен половине BC согласно свойствам медианы. Тогда, по теореме Пифагора

Поскольку AC = 2x, CD = y (так как медиана делит катет на две равные части), то
4×2 + y2 = 9

Одновременно, рассмотрим прямоугольный треугольник EBC. У него также угол С прямой по условию задачи, катет BC является общим с катетом BC исходного треугольника ABC, а катет EC по свойству медианы равен половине катета AC исходного треугольника ABC.
По теореме Пифагора:
EC2 + BC2 = BE2

Поскольку EC = x (медиана делит катет пополам), BC = 2y, то
x2 + 4y2 = 16

Так как треугольники ABC, EBC и ADC связаны между собой общими сторонами, то оба полученных уравнения также связаны между собой.
Решим полученную систему уравнений.
4×2 + y2 = 9
x2 + 4y2 = 16

Сложим оба уравнения (впрочем, можно было выбрать и любой другой способ решения).
5×2 + 5y2 = 25
5( x2 + y2 ) = 25
x2 + y2 = 5

Обратимся к исходному треугольнику ABC. По теореме Пифагора
AC2 + BC2 = AB2

Так как длина каждого из катетов нам “известна”, мы приняли, что их длина равна 2x и 2y, то есть
4×2 + 4y2 = AB2
Так как оба слагаемых имеют общий множитель 4, вынесем его за скобки
4 ( x2 + y2 ) = AB2
Чему равно x2 + y2 мы уже знаем (см. выше x2 + y2 = 5), поэтому просто подставим значения вместо x2 + y2

AB2 = 4 х 5
AB2 = 20
AB = √20 = 2√5

Ответ: длина гипотенузы равна 2√5

Угол между высотой и медианой треугольника |

| Медіана прямокутного трикутника

Определение. Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).

Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.

На рисунке 1 медианой является отрезок BD.

Утверждение 1. Медиана треугольника делит его на два треугольника равной площади (равновеликих треугольника).

Доказательство. Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

и заметим, что (см. раздел нашего справочника «Площадь треугольника»)

Поскольку отрезок BD является медианой, то

что и требовалось доказать.

Утверждение 2. Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1, считая от вершины треугольника.

Доказательство. Рассмотрим две любых медианы треугольника, например, медианы AD и CE, и обозначим точку их пересечения буквой O (рис. 3).

Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

Теперь рассмотрим четырёхугольник FEDG (рис. 5).

Сторона ED этого четырёхугольника является средней линией в треугольнике ABC. Следовательно,

Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC. Следовательно,

откуда вытекает, что стороны ED и FG четырёхугольника FEDG равны и параллельны. Следовательно, четырехугольник FEDG является параллелограммомСледовательно, четырехугольник FEDG является параллелограммомСледовательно, четырехугольник FEDG является параллелограммом, а у параллелограмма диагонали в точке пересечения делятся пополаму параллелограмма диагонали в точке пересечения делятся пополаму параллелограмма диагонали в точке пересечения делятся пополам (рис.6).

Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1, считая от вершины треугольника.

Следствие. Все три медианы треугольника пересекаются в одной точке.

Доказательство. Рассмотрим медиану AD треугольника ABC и точку O, которая делит эту медиану в отношении 2 : 1, считая от вершины A (рис.7).

Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.

Определение. Точку пересечения медиан треугольника называют центроидом треугольника.

Утверждение 3. Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

Доказательство. Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC, равна площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).

В силу утверждения 1,

что и требовалось доказать.

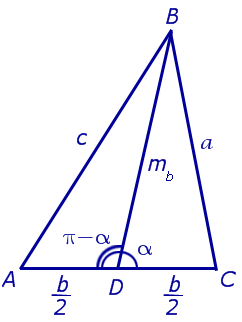
Утверждение 4. Длина медианы треугольника (рис. 10) вычисляется по формуле:

Доказательство. Воспользуемся теоремой косинусов, примененной к треугольникам DBC и ABD:

Складывая эти равенства, получим:

что и требовалось доказать.

Следствие. Длины медиан и длины сторон треугольника связаны формулой

Доказательство. В силу утверждения 4 справедливы равенства:

Складывая эти равенства, получим:

что и требовалось доказать.

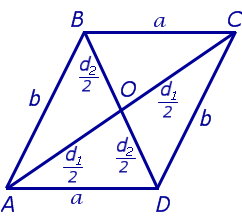
Утверждение 5. В параллелограммепараллелограмме сумма квадратов диагоналей равна сумме квадратов сторон.

Доказательство. Рассмотрим рисунок 11.

Поскольку AO – медиана треугольника ABD, а DO – медиана треугольника ADC, то, в силу утверждения 4, справедливы равенства:

Складывая эти равенства, получим

что и требовалось доказать.

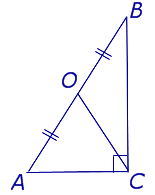
Утверждение 6. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы (рис. 12).

Доказательство. Продолжим медиану CO за точку O до точки D так, чтобы было выполнено равенство CO = OD, и соединим полученную точку D с точками A и B (рис. 13).

Получим четырехугольник ADBC, диагонали которого в точке пересечения делятся пополам. В силу признака параллелограммапризнака параллелограммапризнака параллелограмма заключаем, что четырехугольник ADBC является параллелограммом, а поскольку полученный параллелограмм содержит прямой угол C, то и все его углы прямые, следовательно, четырехугольник ADBC – прямоугольникпрямоугольник. Поскольку диагонали прямоугольника равны, получаем равенства:

что и требовалось доказать.

Следствие. Середина гипотенузы прямоугольного треугольника является центром описанной около треугольника окружности (рис. 14).

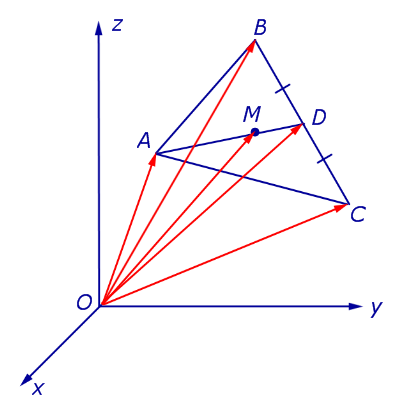
Утверждение 7. Рассмотрим в пространстве или на плоскости декартову систему координат с началом в точке O и произвольный треугольник ABC. Если обозначить буквой M точку пересечения медиан этого треугольника (рис.15), то будет справедливо равенство

Доказательство. По свойствам векторов

что и требовалось доказать.

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Источник