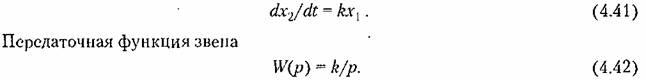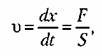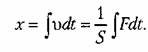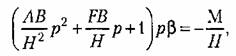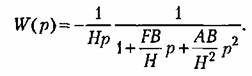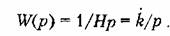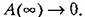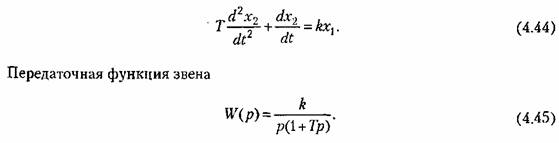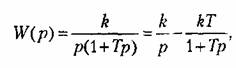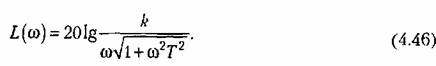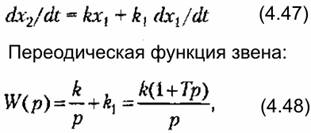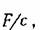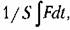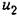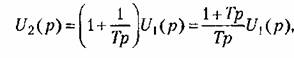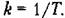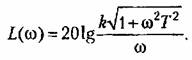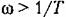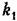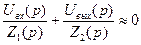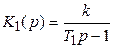Что можно сказать об устойчивости системы содержащей интегрирующее звено
Интегрирующие звенья
1. Идеальное интегрирующее звено. Звено описывается дифференциальным уравнением
Такое звено является идеализацией реальных интегрирующих звеньев, часть которых будет рассмотрена ниже. Примеры интегрирующих звеньев приведены на рис. 4.18. Часто в качестве такого звена используется операционный усилитель в режиме интегрирования (рис. 4.18, а). Интегрирующим звеном является также обычный гидравлический демпфер (рис. 4.18, б). Входной величиной здесь является сила F, действующая на поршень, а выходной — перемещение поршня х2. Так как скорость движения поршня пропорциональна приложенной силе (без учета инерционных сил):
где 5 — коэффициент скоростного сопротивления; его перемещение будет пропорциональным интегралу от приложенной силы:
Часто в качестве интегрирующего звена используется интегрирующий привод (рис, 4.18, г). Это особенно удобно делать при необходимости длительного иитегрирования
(часы, дни и даже месяцы), например в автоматических путепрокладчиках и навигационных системах.
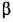
Из уравнений гироскопа, приведенных в предыдущем параграфе, можно получить:
откуда передаточная функция для угла прецессии
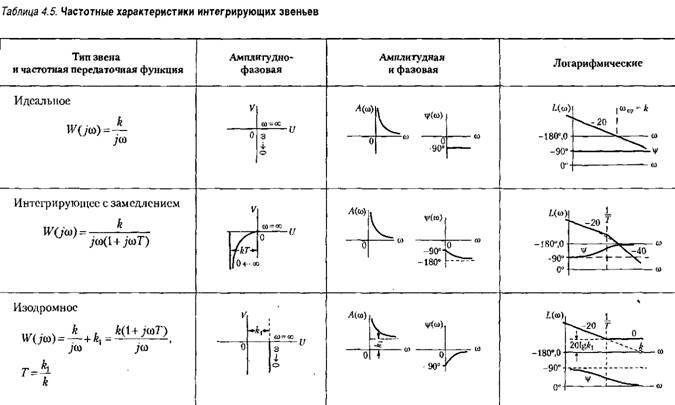
Временные характеристики звена приведены в табл. 4.4, а частотные — в табл. 4.5.
Амплитудно-фазовая характеристика сливается с отрицательной частью мнимой оси.
Построение л, а. х. делается но выражению
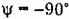
2. Интегрирующее звено с замедлением. Звено описывается дифференциальным уравнением
Примером такого звена является двигатель (рис. 4.10, а), если в качестве выходной величины рассматривать не угловую скорость, а угол поворота, являющийся интегралом от угловой скорости. К такому же типу звена сводятся демпфер (рис. 4.18, 6) серводвигатель (рис. 4.18, в), интегрирующий привод (рис. 4,18, г), если более точно рассматривать их уравнения движения, и др.
Интегрирующее звено с замедлением можно представить как совокупность двух включенных последовательно звеньев — идеального интегрирующего и апериодического первого порядка.
Для нахождения временных характера удобно передаточную функцию представить в виде алгебраической суммы
что позволяет представить решение дифференциального уравнения (4.44) в виде суммы решений для идеального интегрирующего звена и апериодического звена нервого порядка.
Временные характеристики приведены в табл.
4.4, а частотные — в табл. 4.5.
Л.а.х. строится по выражению
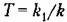
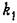
где с — жесткость пружины, и перемещения поршня
где 5 — коэффициент скоростного сопротивления демпфера.
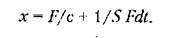
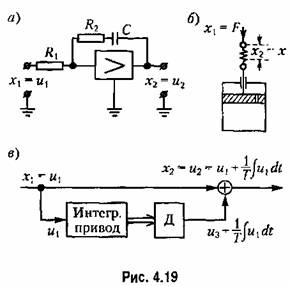
При использовании операционного усилителя (рис. 4.19, а) изодромное звено может быть получено посредством применения КС-цепи в обратной связи.
Таким образом, для схемы, изображенной на рис. 4.19, в,
Временные характеристики звена представлены в табл. 4.4, а частотные — в табл. 4.5.
Л. а. х. строится по выражению
Из рассмотрения л. а. х. и л. ф. х. видно, что в области малых частот (меньших, чем сопрягающая частота) звено ведет себя как идеальное интегрирующее и тем точнее, чем меньше частота.
Свойство звена вводить интегрирующее действие в области малых частот используется для улучшения качественных показателей систем автоматического регулирования (см. главу 9).
Что можно сказать об устойчивости системы содержащей интегрирующее звено
Передаточная функция звена
Такое звено является идеализацией реальных интегрирующих звеньев, часть которых будет рассмотрена ниже. Примеры интегрирующих звеньев приведены на рис. 4.21. Часто в качестве такого звена используется операционный усилитель в режиме интегрирования (рис. 4.21, а). Интегрирующим звеном является также обычный гидравлический демпфер (рис. 4.21, б). Входной величиной здесь является сила 

(кликните для просмотра скана)
(кликните для просмотра скана)
где 
Часто в качестве интегрирующего звена используется интегрирующий привод (рис. 4.21, г). Это особенно удобно делать при необходимости длительного интегрирования (часы, дни и даже месяцы), например в автоматических путепрокладчиках и навигационных системах.
Интегрирующим звеном является также гироскоп (рис. 4.17, г), если в качестве входной величины рассматривать момент М на оси а, а в качестве выходной — угол поворота оси прецессии 
Из уравнений гироскопа, приведенных в предыдущем параграфе, можно получить:
откуда передаточная функция для угла прецессии
В случае пренебрежения влиянием нутационных колебаний передаточная функция гироскопа будет равна
Временнйе характеристики звена приведены в табл. 4.4, а частотные — в табл. 4.5.
Амплитудная частотная характеристика показывает, что звено пропускает сигнал тем сильнее, чем меньше его частота. При 
частотной передаточной функции стремится к бесконечности, а при
Амплитудно-фазовая характеристика для положительных частот сливается с отрицательной частью мнимой оси.
Построение л. а. х. делается по выражению
Л. а. х. представляет собой прямую с отрицательным наклоном 


2. Интегрирующее звено с замедлением.
Передаточная функция звена
Примером такого звена является двигатель (рис. 4.13, а), если в качестве выходной величины рассматривать не угловую скорость, а угол поворота, являющийся интегралом от угловой скорости. К такому же типу звена сводятся демпфер (рис. 4.21, б), серводвигатель (рис. 4.21, в), интегрирующий привод (рис. 4.21, г), если более точно рассматривать их уравнения движения, и др.
Интегрирующее звено с замедлением можно представить как совокупность двух включенных последовательно звеньев — идеального интегрирующего и апериодического первого порядка.
Для нахождения временных характеристик удобно передаточную функцию представить в виде алгебраической суммы
что позволяет представить решение дифференциального уравнения (4.46) в виде суммы решений для идеального интегрирующего звена и апериодического звена первого порядка.
Временные характеристики приведены в табл. 4.4, а частотные — в табл. 4.5.
Л. а. х. строится по выражению
Асимптотическая л. а. х. представляет собой две прямые с отрицательными наклонами 

3. Изодромное звено.
Передаточная функция звена
где 
Из этих выражений видно, что звено можно условно представить в виде совокупности двух звеньев, действующих параллельно, — идеального интегрирующего с коэффициентом передачи к и безынерционного с коэффициентом передачи к
Примеры изодромных звеньев изображены на рис. 4.22. Таким звеном может быть комбинация пружины с демпфером (рис. 4.22, б).
В качестве входной величины здесь рассматривается прикладываемая сила 
где с — жесткость пружины, и перемещения поршня
где 
Результирующее перемещение точки
При использовании операционного усилителя (рис. 4.22, а) изодромное звено может быть получено посредством применения 
В системах управления часто находят применение изодромные звенья, построенные на базе интегрирующего привода (рис. 4.22, в). В этом случае входное напряжение 

суммируется с напряжением 
Таким образом, для схемы, изображенной на рис. 4.22, в,
где Т — коэффициент пропорциональности между скоростью изменения выходного напряжения датчика интегрирующего привода и напряжением
Таблица 4.4. Временные характеристики интегрирующих звеньев
на его входе. Коэффициент передачи идеального интегрирующего звена в этом случае равен
Временные характеристики звена представлены в табл. 4.4, а частотные — в табл. 4.5.
Л. а. х. строится по выражению
Асимптотическая л. а. х. представляет собой две прямые: с отрицательным наклоном 


Из рассмотрения л. а. х. и л. ф. х. видно, что в области малых частот (меньших, чем сопрягающая частота) звено ведет себя как идеальное интегрирующее и тем точнее, чем меньше частота.
В области больших частот (больших, чем сопрягающая частота) звено ведет себя как безынерционное с коэффициентом передачи
Свойство звена вводить интегрирующее действие в области малых частот используется для улучшения качественных показателей систем автоматического регулирования (см. главу 9).
Интегрирующее звено
Интегрирующим звеном называется типовое звено, которое описывается уравнением
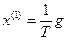
где 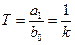
Иногда уравнение интегрирующего звена записывают в виде
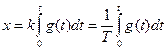
т.е. выходная величина является интегралом от входной величины.
Передаточная функция интегрирующего звена имеет вид
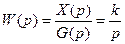
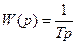
Полагая в выражениях (5.30) и (5.31) p=jw, получим выражение для частотной передаточной функции звена
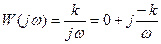
Совершенно очевидно, что вещественная частотная характеристика U(w)=0, а мнимая частотная характеристика 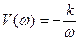
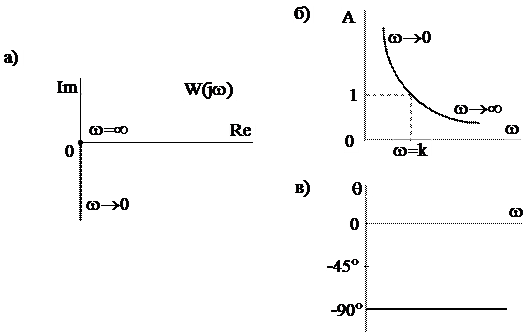 |
Рис.5.10. Частотные характеристики интегрирующего звена:
Амплитудная и фазовая частотные характеристики определяются соответственно выражениями:
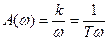
Из выражения (5.33) следует, что при w®0 A(w)®¥, при 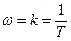
Как следует из рис.5.10,б и выражения (5.33), характеристика A(w) является разносторонней гиперболой, асимптотами которой служат оси координат.
Логарифмические частотные характеристики интегрирующего звена определяются выражениями:
L(w) = 20 lg A(w) = 20 lg k – 20 lg w (5.35)
Следовательно, наклон L(w) интегрирующего звена равен –20дБ\дек. Если k¹1, то характеристика смещается параллельно самой себе на 20lgk вверх при k>1 или вниз при k
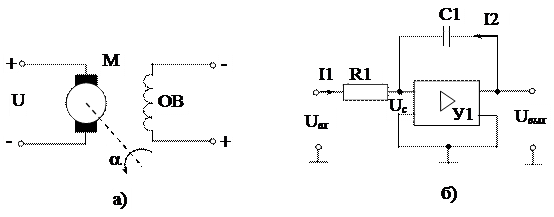
Рис.5.12. Примеры интегрирующих звеньев
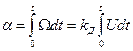
2. Электронный усилитель постоянного тока (УПТ) с большим коэффициентом усиления по напряжению и с конденсатором в цепи отрицательной обратной связи (рис.5.12,б).
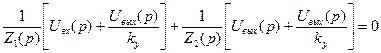
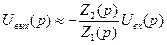
Теперь найдем передаточную функцию усилителя
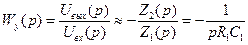
Видим, что это – передаточная функция интегрирующего звена с постоянной времени Т= R1 C1.
Пример 4.2.. Интегрирующее звено соединяется последовательно с инерционным звеном



Пример 4.1.
Интегрирующее звено соединяется последовательно с инерционным звеном. Какова будет передаточная функция системы?
Передаточные функции звеньев:
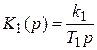
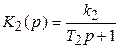
Согласно формуле (4.1), передаточная функция системы
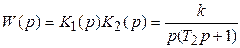
Неустойчивое звено с передаточной функцией
последовательно соединяется с неустойчивым звеном, имеющим передаточную функцию.
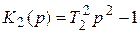
Выяснить, при каком условии система будет устойчивой.
Передаточная функция системы
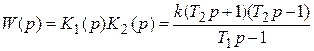
Пример 4.3.
Интегрирующее звено соединяется последовательно с реальным дифференцирующим звеном. Найти передаточную функцию.
Передаточные функции звеньев:
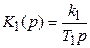
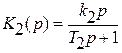
Перемножая, получаем передаточную функцию соединения:
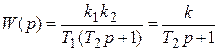
(Пример показывает, что инерционное звено можно заменить последовательным соединением интегрирующего и реального дифференцирующего звеньев).