Что можно сказать об углах величины которых равны 7 класс
1. Как называют фигуру образованную точкой принадлежащей прямой, и одной из частей, на которые эта точка делит прямую? Как при этом называет данную точку? 2. Как обозначают луч? 3. Как называют фигуру, образованную двумя лучами с общим началом и одной из частей, на которые эти лучи делят плоскость? 4.Как обозначают угол? 5. Какой угол называют развернутым? 6. Как называют части, на которые прямая делит плоскость? 7. Какие два угла называют равными? 8. Что называют биссектрисой угла? 9. В каких единицах измеряют углы? 10. Какова градусная мера развёрнутого угла? 11. Как называют угол, градусная мера которого равна 90 градусов? 12. Какой угол называют тупым? 13. Какой угол называют острым? 14. Какие величины равных углов? 15. Что можно сказать об углах. величины которых равны? 16. Сформулируйте основное свойство величины углов.
Ответ оставил Гуру
1) Луч
2) Лучи обозначаются через две латинские буквы или одной маленькой латинской буквой. 3) Дополнительные лучи – это лучи, имеющие общее начало, противоположные направления и лежащие на одной прямой
4) Угол
5) Одной заглавной латинской буквой ( Вершина угла ), Двумя малыми латинскими буквами ( Стороны Угла )
6) Если его обе плоскости лежат на одной прямой
7) Две полуплоскости
8) два угла называются равными — если их можно совместить наложением
9) Биссектриса угла — луч с началом в вершине угла, делящий угол на две равные части
10) В Градусах
11) 180 Градусов
12) Острый 13) У которого Градус меньше 90
14) У которого градус больше 120
15) 1) равные углы имеют равные величины равные величины 2) если он состоит из двух углов
16) Равные углы имеют равные величины
17)…
Если тебя не устраивает ответ или его нет, то попробуй воспользоваться поиском на сайте и найти похожие ответы по предмету Геометрия.
Что можно сказать об углах величины которые равны
Ответы 5
ответ: Если все углы равны в треугольнике то он равносторонний, если в многоугольнике то он правильный
2) лучи обозначаются через две латинские буквы или одной маленькой латинской буквой.
3) дополнительные лучи – это лучи, имеющие общее начало, противоположные направления и лежащие на одной прямой
5) одной заглавной латинской буквой ( вершина угла ), двумя малыми латинскими буквами ( стороны угла )
6) если его обе плоскости лежат на одной прямой
7) две полуплоскости
9) биссектриса угла — луч с началом в вершине угла, делящий угол на две равные части
13) у которого градус меньше 90
14) у которого градус больше 120
15) 1) равные углы имеют равные величины равные величины 2) если он состоит из двух углов
16) равные углы имеют равные величины
Что можно сказать об углах величины которых равны 7 класс
Определение 1. Угол − это геометрическая фигура,которая состоит из двух лучей, исходящих из одной точки.
Лучи называются сторонами угла, а их общее начало − вершиной угла.
 |
Обозначение угла
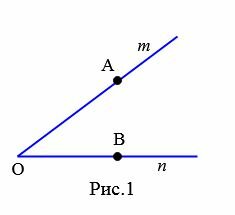
На рисунке 1 изображен угол с вершиной O и сторонами m и n. Данный угол обозначают \( \small ∠mn \) или \( \small ∠O. \) Если на сторонах угла выбрать точки A и B, то угол можно обозачить так: \( \small ∠AOB \) или \( \small ∠BOA. \)
Развернутый угол. Внутренняя и внешняя область угла
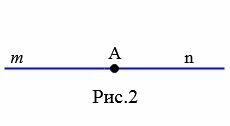
Угол называется развернутым, если его стороны находятся на одной прямой. На рисунке 2 изображен развернутый угол с вершиной А и сторонами m и n.
 |
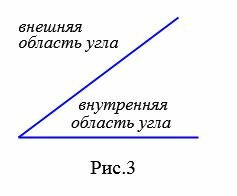
Любой угол разделяет плоскость на две части. Если угол неразвернутый, то меньшая из частей называется внутренней областью, а другая − внешней областью этого угла (Рис.3).
 |
Если угол развернутый, то любую из двух частей, на которые разделяет угол данную плоскось можно считать внутренней областью угла.
Фигуру, состоящую из угла и его внутренней области также называют углом.
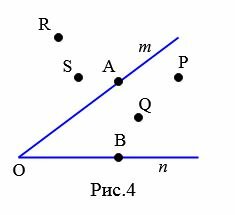
На рисунке 4 точки P и Q лежат внутри угла mn (т.е. во внутренней области угла), точки R и S лежат вне угла mn (т.е. во внешней области угла), а точки A и B на сторонах этого угла.
 |
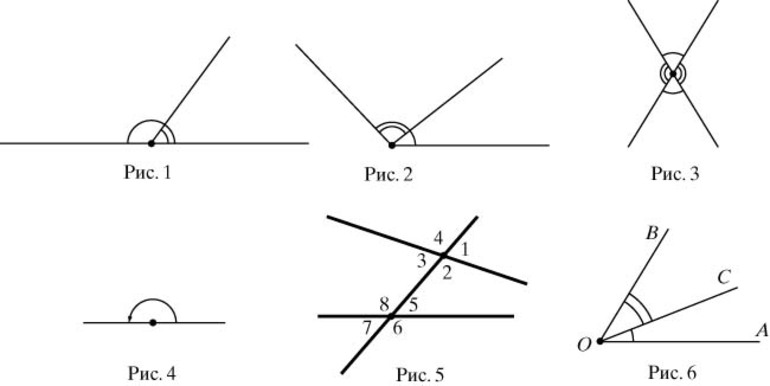
Типы углов
В зависимости от величин, углы бывают следующих типов (Рис.5):
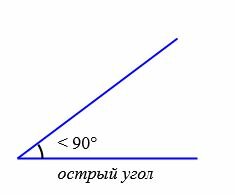 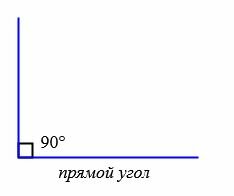 |
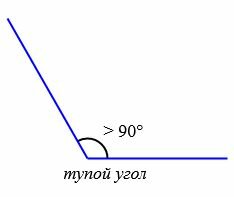  |
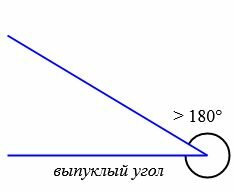 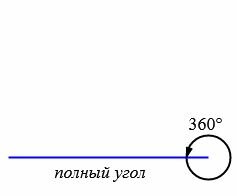 |
Сравнение углов
Углы можно сравнить, то есть определить равны ли они или какой угол меньше а какой больше. Чтобы определить равны ли углы или нет нужно наложить один угол на другой так, чтобы сторона одного угла совместилась со стороной другого угла а две другие оказались по одну сторону от совместившихся сторон. Если две другие стороны также совместились, то углы полностью совместятся и,следовательно они равны. Если же эти стороны не совместяться, то меньшим считается тот угол, который является частью другой.
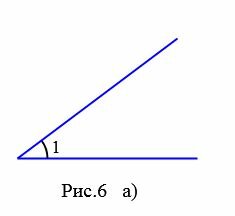 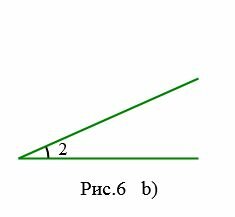 |
На рисунках 6a и 6b представлены два угла: 1 и 2. На рисунке 7 угол 2 является частью угла 1, следовательно угол 2 меньше угла 1. Это пишется так: \( \small ∠2 \lt \angle 1. \)
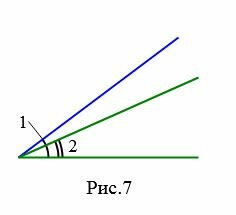 |
Градусная мера угла
Измерение углов основана на сравнении их с углом, принятым за единицу измерения. За единицей измерения углов примнимают градус, которая является \( \small \frac <1> <180>\) частью развернутого угла. Положительное число, показывающая, сколько раз градус и его части помещаются в данном угле называвется градусной мерой угла. Для измерения углов используют транспортир (Рис.8).
 |
Для угла AOB, градусная мера которого равна 120° говорят «угол AOB равен 120° » и пишут: \( \small ∠AOB=120 °. \) Очевидно, что градусная мера развернутого угла равна 180°. \( \small \frac <1> <60>\) часть градуса называется минутой и обозначается так: » ‘ «. \( \small \frac <1> <60>\) часть минуты называется секундой и обозначается так: » » «. Если градусная мера угла AOB равна 56 градусов 6 минут и 43 секунды, то пишут: \( \small \angle AOB=56°6’43». \)
Отметим, что равные углы имеют равные градусные меры. Если углы разные, то меньший угол имеет меньшую градусную меру.
Базисные понятия
Угол — простая фигура в геометрии, образуемая двумя лучами, следующими из некоторой точки. Эту точку определяют как его вершину. Название «угол» может относиться к части плоскости, объединяющей все лучи, исходящие из вершины фигуры. Такое обозначение может также иметь угловая мера, чаще всего определяемая в градусах.
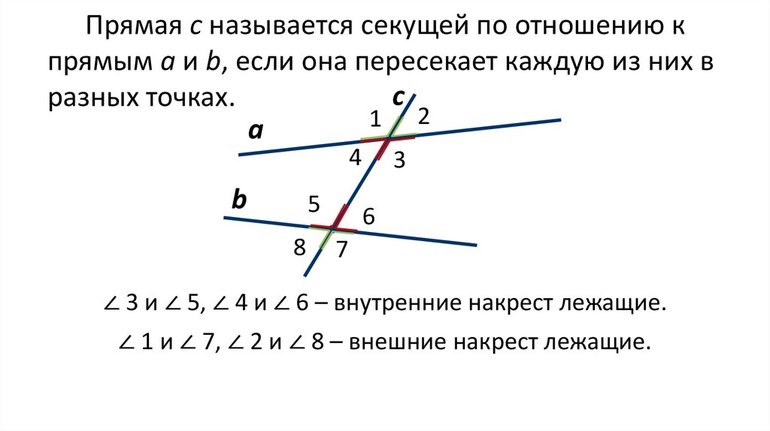
В геометрии существует несколько критериев, позволяющих выделить разные типы угловых фигур. Они бывают тупыми и острыми, смежными или вертикальными. Для углов, образуемых в результате пересечения секущей линией двух прямых, в качестве такого критерия берется свойство взаимных соотношений формируемых при этом фигур. При рассмотрении произвольного геометрического рисунка, образованного двумя прямыми линиями и секущей, можно увидеть 4 пары соответственных, по 2 пары внутренних и внешних накрест лежащих или односторонних угловых фигур. Все эти элементы могут быть как тупоугольными, так и остроугольными.
Углы, образующиеся при пересечении прямых
Чтобы понять, как выглядят соответственные углы, а также уметь находить их на любых геометрических рисунках, нужно хорошо усвоить разницу между типами фигур, образованных секущей линией. Кроме того, следует обратить внимание на наличие внутренней и внешней областей. Первая зона ограничивается площадью между двумя прямыми, второй внешней областью считается неограниченное пространство снаружи от этих двух линий.
Итак, образованным тремя прямыми линиями угловым фигурам можно дать следующие определения:
Более наглядное представление об этом типе углов можно получить, если секущую изобразить в виде направленного вектора. Парные угловые элементы расположены в одном направлении относительно прямых, пересеченных третьей линией.
Чтобы окончательно разобраться в вопросе, нужно усвоить понятие соответствия с математической точки зрения. В геометрии это свойство двух фигур, у которых углы, стороны или точки одного объекта аналогичны соответствующим элементам другого объекта. Аналогия проявляется не в их равенстве, а во взаимном соотношении элементов. О соответствии углов говорит аналогичное пространственное положение лучей в местах пересечения прямых с третьей секущей линией. Таким образом, речь идет об элементах, имеющих одинаковое относительное положение.
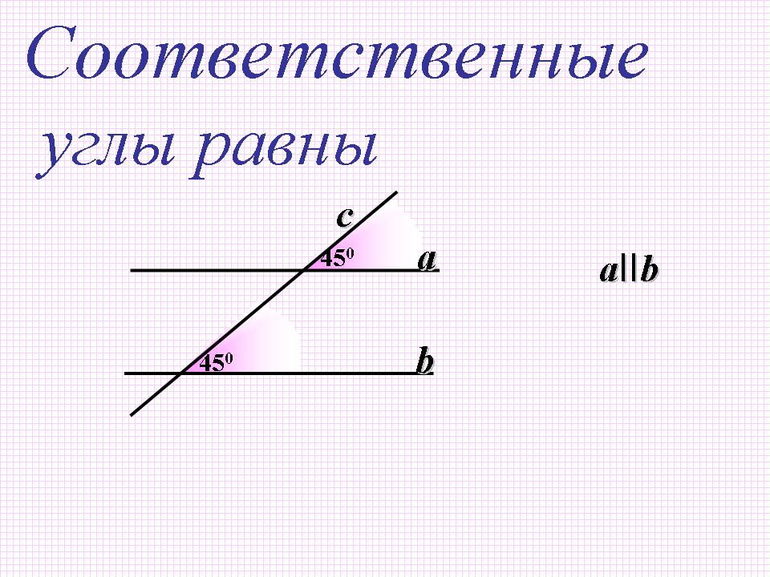
Соответственные углы при параллельных прямых
Свойства фигур, формирующихся при пересечении секущей параллельных прямых, давно описаны в планиметрии. Известно, что соответственные накрест лежащие угловые элементы при параллельных прямых равны. Сложение угловых величин односторонних фигур дает значение 180 градусов. В геометрии применяется формула для расчета суммы соответственных парных угловых фигур при условии параллельности двух линий. Для определения этого параметра из числа 360 надо вычесть удвоенную угловую величину одностороннего угла, прилежащего к любому из пары рассчитываемых соответственных угловых элементов.
Равные соответственные углы указывают на параллельность прямых. Справедливость этого признака вытекает из следующих утверждений:
Доказательство можно развернуть и в обратном направлении. Параллельные линии при пересечении третьей прямой формируют одинаковые по величине соответственные углы. Это утверждение известно как свойство параллельных линий.
Такого рода свойства встречаются в описаниях признаков и теорем. Их равенство — часть доказательств равенства и подобия треугольников. В свою очередь, используя признаки подобных и равных треугольников, можно обосновывать доказательства сложных теорем, находить решения сложных задач, править возможные ошибки.
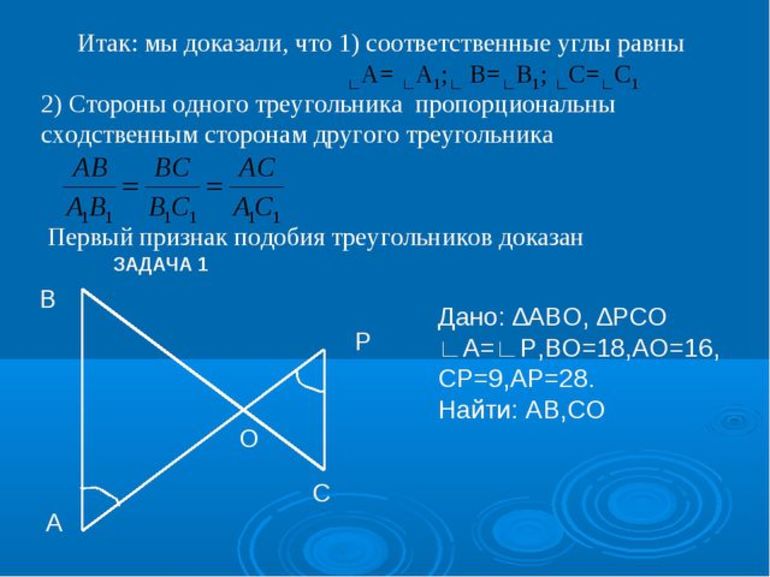
Доказательство подобия треугольников
Существует три признака, по которым могут быть определены подобные треугольники. Во-первых, подобие подтверждается пропорциональностью всех трех сторон треугольников. Во-вторых, подобными считаются треугольники, имеющие две пропорциональные стороны, угловая величина между которыми равна соответствующему элементу второго треугольника. В-третьих, подобие подтверждается, когда имеет место равенство двух углов обоих треугольников.
Рассмотрим доказательство этого признака, в ходе которого применяется свойство тождественности соответственных угловых объектов:
Подобного рода рассуждения и доказательства, учитывающие свойства соответственных угловых фигур, учитываются при решении разного рода задач.
В сложных планиметрических фигурах в качестве секущей, формирующей этот тип геометрических объектов, может выступать медиана, биссектриса треугольника или какие-либо другие линии. Для решения таких задач требуется хорошее знание базовых понятий, признаков, свойств, аксиом, позволяющее заметить определенные соотношения и закономерности в том или ином задании.