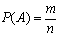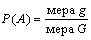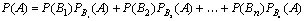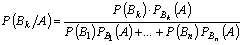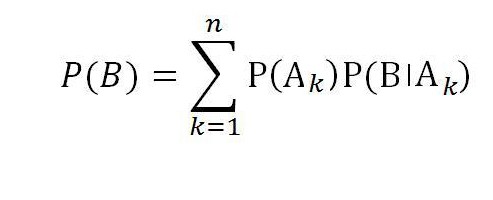Что можно сказать о вероятности достоверного события

Важнейшие свойства вероятностей. 1) вероятность достоверного события W равна 1

1) вероятность достоверного события W равна 1.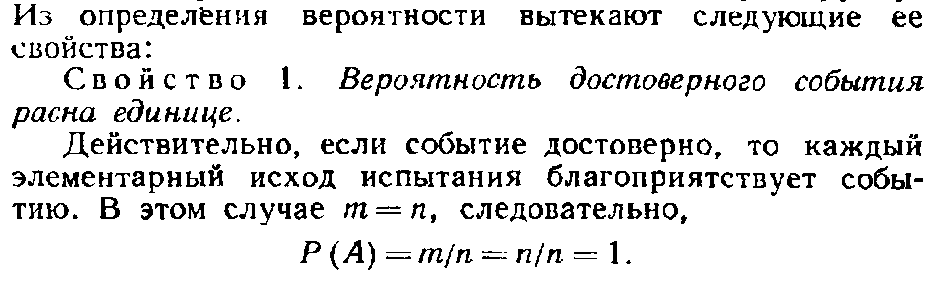
2) вероятность невозможного события равна 0.

3) Вероятность любого случайного события есть число, заключенное между 0 и 1.

4)Вероятность суммы несовместных событий равна сумме вероятностей этих событий (так как события А и В несовместимы, то общих исходов у них нет, а значит исходы события А+В разбиты на 2 непересекающихся группы).

5) Вероятность суммы совместимых 2 событий равна суме вероятностей этих 2 событий без вероятности их произведения (так как события совместимы, то у них есть общие исходы которые нельзя считать дважды).

6) Противоположным событием А называется событие не-А (с чертой), которое включает в себя все исходы из W, не включенные в А (Р(А)+Р(не-А)=1).

7)Вероятность события Р(А) = (1 – Р(не-А)), и наоборот.

Источник

Тема 8. СОБЫТИЕ И ВЕРОЯТНОСТЬ

8.1. Понятие о случайном событии

Наблюдение явления, опыт, эксперимент, которые можно провести многократно, в теории вероятностей принято называть испытанием. Примеры: сдача экзамена, наблюдение за дорожно-транспортными происшествиями, выстрел из винтовки, бросание игрального кубика, педагогический эксперимент.

Результат, исход испытания называется событием. Примеры: успешная сдача экзамена, дорожно-транспортные происшествия со смертельным исходом, попадание в цель, появление того или иного числа очков на брошенной игральной кости, получение результата при проведении педагогического эксперимента.

Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании. Примеры: совместные события: идет дождь и идет снег, человек ест и человек читает, число целое и четное; несовместные события: день и ночь, человек читает и человек спит, число иррациональное и четное.

Два события называются противоположными, если в данном испытании они несовместны и одно из них обязательно происходит. Примеры: если сейчас день, то сейчас не ночь; если человек спит, то в данный момент он не читает; если число иррациональное, то оно не является четным.

Событие называется достоверным, если в данном испытании оно является единственно возможным его исходом. Событие называется невозможным, если в данном испытании оно заведомо не может произойти. Примеры: если в урне все шары белые, то достать белый шар является достоверным событием, а достать черный шар является невозможным событием; если человек прыгнул в воду, то выйти мокрым является достоверным событием, а выйти сухим является невозможным событием.

Событие называется случайным, если его наступление или ненаступление в некотором испытании (эксперименте) зависит от ряда случайных факторов. Примеры: успешная сдача экзамена; выигрыш в лотерее; рождения мальчика или девочки; всхожесть семян; попадание в цель и т. д.

8.2. Определение вероятности

События, образующие полную группу попарно несовместных и равновозможных событий, будем называть элементарными событиями.

Классическое определение вероятности

Вероятностью P(A) события A называется отношение числа элементарных событий m, благоприятствующих событию A, к числу всех элементарных событий n:

Вероятность достоверного события равна 1.
Вероятность невозможного события равна 0.
Вероятность случайного события больше 0 и меньше 1.

Статистическое определение вероятности

Классическое определение вероятности не является пригодным для изучения произвольных случайных событий. Например, оно неприемлемо, если результаты испытания не равновозможны. В таких случаях используется статистическое определение вероятности. Пусть проводится n опытов, событие A наступило m раз, тогда

,

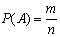
Геометрическое определение вероятности

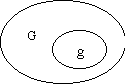
Если в результате проведения испытаний наблюдается произвольный исход из некоторого бесконечного множества, то можно сказать, что пространство элементарных исходов может быть некоторой областью G, а под событием А можно понимать исходы, входящие в область g. Пусть на область G наугад брошена «точка»; приняв равновозможность вариантов, естественно считать, что вероятность попадания в область g можно найти по формуле, называемой геометрической вероятностью:

Области могут быть различной размерности (одно-, двух- или трехмерного измерения) и, в зависимости от выбора размерности меры, могут принимать значения либо длины, либо площади, либо объема. Для конкретного испытания размерность мер g и G должна быть одна.

8.3. Свойства вероятности

Теорема. Вероятность суммы двух несовместных событий A и B равна сумме вероятностей этих событий: P (A + B) = P(A) + P(B).

Следствие. Сумма вероятностей противоположных событий А и равна единице:

Вероятность суммы полной группы событий равна 1.

Произведением событий А и В называется событие С = АВ, состоящее в том, что в результате испытания произошло и событие А и событие В.

Два события A и B называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае события A и B называются зависимыми.

Чаще всего зависимые испытания происходят тогда, когда тянут из одной колоды, не возвращая карты в колоду, вытаскивают из одной урны и т. д.

Теорема. Вероятность произведения двух независимых событий A и B равна произведению их вероятностей:

Теорема. Вероятность произведения двух зависимых событий A и B равна произведению вероятности одного из них на условную вероятность другого, найденного в предположении, что первое событие уже наступило:

Теорема. Вероятность суммы двух совместных событий A и B равна сумме вероятностей этих событий минус вероятность их произведения

Теорема (формула полной вероятности). Вероятность события A, которое может наступить лишь при условии появления одного из n попарно несовместных событий B1, B2,…, Bn, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A:

Вопросы

1. Может ли событие быть одновременно и невозможным и достоверным?
2. Входит ли в понятие суммы событий (А + В) событие, состоящее в одновременном наступлении события А и события В?
3. Приведите пример полной группы событий для выбранного Вами испытания.
4. Исходя из формулы определения вероятности, объясните, почему значение вероятности находится в пределах от 0 до 1.
5. Часто ли случается, что наступление какого-либо события зависит от ряда причин? Приведите пример.
6. С помощью какой формулы можно выяснить наиболее вероятную причину уже наступившего события?

Источник

Что можно сказать о вероятности достоверного события

Событиями являются и результаты различных опытов, наблюдений и измерений.

1) из ящика с разноцветными шарами наугад вытаскивают белый шар;

2) на один из приобретенных лотерейных билетов выпал выигрыш;

3) при бросании игральной кости выпала цифра 6.

События делятся на достоверные, случайные и невозможные.

Достоверным называется событие, если оно обязательно произойдет в данном испытании.

Случайным называется событие, если оно может произойти, но может и не произойти в данном испытании.

Невозможным называется событие, если оно не может произойти в данном испытании.

За единицу принимают вероятность достоверного события, а вероятность невозможного события считают равной нулю. Тогда вероятность Р любого события А удовлетворяет неравенству:

Несовместными называются события, если появление одного из них

Пример. Опыт состоит в подбрасывании монеты, событие А – выпадение орла, событие В – выпадение решки. Эти события несовместны, равновозможны и единственно возможны.

Равновозможными называются события, если ни одно из них не является более возможным, чем другое.

Единственно возможными называются события, если в результате опыта хотя бы одно из них обязательно наступит. Говорят, что единственно возможные события образуют полную группу событий .

Рассмотрим классический метод определения вероятности некоторого случайного события. Пусть в результате некоторого опыта могут наступить события А₁, А₂, А₃, …, А_n (элементарные исходы опыта), которые являются:

1)единственно возможными, т.е. в результате опыта хотя бы одно из них обязательно наступит;

2)несовместными, т.е. появление одного из них исключает появление всех остальных;

3)равновозможными, т.е. не существует никаких причин, в связи с которыми одно из событий появлялось бы чаще, чем остальные.

Пусть при появлении некоторых из этих событий наступает событие А. Обозначим число таких событий k (k≤n). А при появлении остальных (n-k) событий событие А не наступает. Говорят, что k событий (элементарных исходов), при которых появляется событие А, благоприятствуют событию А, а остальные (n-k) событий не благоприятствуют ему.

Вероятностью события А называется отношение числа k элементарных исходов, благоприятствующих этому событию, к общему числу элементарных исходов испытания n, если они равновозможны, несовместны и единственно возможны.

Источник

Теория вероятностей, формулы и примеры

Тема непростая, но если вы собираетесь поступать на факультет, где нужны базовые знания высшей математики, освоить материал — must have. Тем более, все формулы по теории вероятности пригодятся не только в универе, но и при решении 4 задания на ЕГЭ. Начнем!

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные понятия

Французские математики Блез Паскаль и Пьер Ферма анализировали азартные игры и исследовали прогнозы выигрыша. Тогда они заметили первые закономерности случайных событий на примере бросания костей и сформулировали теорию вероятностей.

Когда мы кидаем монетку, то не можем точно сказать, что выпадет: орел или решка.

Но если подкидывать монету много раз — окажется, что каждая сторона выпадает примерно равное количество раз. Из чего можно сформулировать вероятность: 50% на 50%, что выпадет «орел» или «решка».

Теория вероятностей — это раздел математики, который изучает закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

Вероятность — это степень возможности, что какое-то событие произойдет. Если у нас больше оснований полагать, что что-то скорее произойдет, чем нет — такое событие называют вероятным.

Ну, скажем, смотрим на тучи и понимаем, что дождь — вполне себе вероятное событие. А если светит яркое солнце, то дождь — маловероятное или невероятное событие.

Случайная величина — это величина, которая в результате испытания может принять то или иное значение, причем неизвестно заранее, какое именно. Случайные величины можно разделить на две категории:

Вероятностное пространство — это математическая модель случайного эксперимента (опыта). Вероятностное пространство содержит в себе всю информацию о свойствах случайного эксперимента, которая нужна, чтобы проанализировать его через теорию вероятностей.

Формулы по теории вероятности

Теория вероятности изучает события и их вероятности. Если событие сложное, то его можно разбить на простые составные части — так легче и быстрее найти их вероятности. Рассмотрим основные формулы теории вероятности.

Случайные события. Основные формулы комбинаторики

Классическое определение вероятности

Вероятностью события A в некотором испытании называют отношение:

P (A) = m/n, где n — общее число всех равновозможных, элементарных исходов этого испытания, а m — количество элементарных исходов, благоприятствующих событию A

Таким образом, вероятность любого события удовлетворяет двойному неравенству:

Пример 1. В пакете 15 конфет: 5 с молочным шоколадом и 10 — с горьким. Какова вероятность вынуть из пакета конфету с белым шоколадом?

Так как в пакете нет конфет с белым шоколадом, то m = 0, n = 15. Следовательно, искомая вероятность равна нулю:

Неприятная новость для любителей белого шоколада: в этом примере событие «вынуть конфету с белым шоколадом» — невозможное.

Пример 2. Из колоды в 36 карт вынули одну карту. Какова вероятность появления карты червовой масти?

Количество элементарных исходов, то есть количество карт равно 36 (n). Число случаев, благоприятствующих появлению карты червовой масти (А) равно 9 (m).

Геометрическое определение вероятности

Геометрическая вероятность события А определяется отношением:

P(A)= m(A)/m(G), где m(G) и m(A) — геометрические меры (длины, площади или объемы) всего пространства элементарных исходов G и события А соответственно

Чаще всего, в одномерном случае речь идет о длинах отрезков, в двумерном — о площадях фигур, а в трехмерном — об объемах тел.

Пример. Какова вероятность встречи с другом, если вы договорились встретиться в парке в промежутке с 12.00 до 13.00 и ждете друг друга 5 минут?

У нас есть отличные курсы по математике для учеников с 1 по 11 классы — приглашаем на вводный урок!

Сложение и умножение вероятностей

Теорема о сложении вероятностей звучит так: вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:

P(A + B) = P(A) + P(B)

Эта теорема справедлива для любого числа несовместных событий:

Если случайные события A₁, A₂. A_n образуют полную группу несовместных событий, то справедливо равенство:

Произведением событий А и В называется событие АВ, которое наступает тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.

Вторая теорема о сложении вероятностей: вероятность суммы совместных событий вычисляется по формуле:

P(A + B) = P(A) + P(B) − P(AB)

События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема об умножении вероятностей: вероятность произведения независимых событий А и В вычисляется по формуле:

P(AB) = P(A) * P(B)

Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8.

Найдем вероятности того, что формула содержится:

А — формула содержится в первом справочнике;

В — формула содержится во втором справочнике;

С — формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

Ответ: 1 — 0,188; 2 — 0,452; 3 — 0,336.

Формула полной вероятности и формула Байеса

По теореме умножения вероятностей:

Аналогично, для остальных гипотез:

Эта формула называется формулой Байеса. Вероятности гипотез называются апостериорными вероятностями, тогда как — априорными вероятностями.

Пример. Одного из трех стрелков вызывают на линию огня, он производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго — 0,5; для третьего — 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.

Формула Бернулли

При решении вероятностных задач часто бывает, что одно и тоже испытание повторяется многократно, и исход каждого испытания независит от исходов других. Такой эксперимент называют схемой повторных независимых испытаний или схемой Бернулли.

Примеры повторных испытаний:

Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы. А вероятность появления события А в каждом случае постоянна и не изменяется от испытания к испытанию.

Биномиальное распределение — распределение числа успехов (появлений события).

Пример. Среди видео, которые снимает блогер, бывает в среднем 4% некачественных: то свет плохой, то звук пропал, то ракурс не самый удачный. Найдем вероятность того, что среди 30 видео два будут нестандартными.

Опыт заключается в проверке каждого из 30 видео на качество. Событие А — это какая-то неудача (свет, ракурс, звук), его вероятность p = 0,04, тогда q = 0,96. Отсюда по формуле Бернулли можно найти ответ:

Ответ: вероятность плохого видео приблизительно 0,202. Блогер молодец🙂

Наивероятнейшее число успехов

Биномиальное распределение ( по схеме Бернулли) помогает узнать, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов k (появлений события) выглядит так:

Пример. В очень большом секретном чатике сидит 730 человек. Вероятность того, что день рождения наугад взятого участника чата приходится на определенный день года — равна 1/365 для каждого из 365 дней. Найдем наиболее вероятное число счастливчиков, которые родились 1 января.

Формула Пуассона

При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно. Например, 0.97 999 вычислить весьма затруднительно.

В этом случае для вычисления вероятности того, что в n испытаниях событие произойдет k раз, используют формулу Пуассона:

Здесь λ = np обозначает среднее число появлений события в n испытаниях.

Эта формула дает удовлетворительное приближение для p ≤ 0,1 и np ≤10.

События, для которых применима формула Пуассона, называют редкими, так как вероятность, что они произойдут — очень мала (обычно порядка 0,001-0,0001).

При больших np рекомендуют применять формулы Лапласа, которую рассмотрим чуть позже.

Пример. В айфоне 1000 разных элементов, которые работают независимо друг от друга. Вероятность отказа любого элемента в течении времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.

P₁₀₀₀(3) = λ 3 /3! * e −λ = 2 3 /3! * e −2 ≈ 0,18.

Ответ: ориентировочно 0,18.

Теоремы Муавра-Лапласа

Кроме того, пусть P_n(k₁;k₂) — вероятность того, что число появлений события А находится между k₁ и k₂.

Локальная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то

Интегральная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то

Функции Гаусса и Лапласа обладают свойствами, которые пригодятся, чтобы правильно пользоваться таблицей значений этих функций:

Теоремы Лапласа дают удовлетворительное приближение при npq ≥ 9. Причем чем ближе значения q, p к 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность по сравнению с исходной формулой Бернулли.

Источник

Вероятность события. Определение вероятности события

Изначально, будучи всего лишь собранием сведений и эмпирических наблюдений за игрой в кости, теория вероятности стала основательной наукой. Первыми, кто придал ей математический каркас, были Ферма и Паскаль.

От размышлений о вечном до теории вероятностей

Две личности, которым теория вероятностей обязана многими фундаментальными формулами, Блез Паскаль и Томас Байес, известны как глубоко верующие люди, последний был пресвитерианским священником. Видимо, стремление этих двух ученых доказать ошибочность мнения о некой Фортуне, дарующей удачу своим любимчикам, дало толчок к исследованиям в этой области. Ведь на самом деле любая азартная игра с ее выигрышами и проигрышами — это всего лишь симфония математических принципов.

Благодаря азарту кавалера де Мере, который в равной степени был игроком и человеком небезразличным к науке, Паскаль вынужден был найти способ расчета вероятности. Де Мере интересовал такой вопрос: «Сколько раз нужно выбрасывать попарно две кости, чтобы вероятность получить 12 очков превышала 50%?». Второй вопрос, крайне интересовавший кавалера: «Как разделить ставку между участниками незаконченной игры?» Разумеется, Паскаль успешно ответил на оба вопроса де Мере, который стал невольным зачинателем развития теории вероятностей. Интересно, что персона де Мере так и осталась известна в данной области, а не в литературе.

Ранее ни один математик еще не делал попыток вычислять вероятности событий, поскольку считалось, что это лишь гадательное решение. Блез Паскаль дал первое определение вероятности события и показал, что это конкретная цифра, которую можно обосновать математическим путем. Теория вероятностей стала основой для статистики и широко применяется в современной науке.

Что такое случайность

Если рассматривать испытание, которое можно повторить бесконечное число раз, тогда можно дать определение случайному событию. Это один из вероятных исходов опыта.

Опытом является осуществление конкретных действий в неизменных условиях.

Чтобы можно было работать с результатами опыта, события обычно обозначают буквами А, B, C, D, Е…

Вероятность случайного события

Чтобы можно было приступить к математической части вероятности, нужно дать определения всем ее составляющим.

Вероятность события – это выраженная в числовой форме мера возможности появления некоторого события (А или B) в результате опыта. Обозначается вероятность как P(A) или P(B).

В теории вероятностей отличают:

Отношения между событиями

Рассматривают как одно, так и сумму событий А+В, когда событие засчитывается при осуществлении хотя бы одного из составляющих, А или В, или обоих – А и В.

По отношению друг к другу события могут быть:

Если два события могут произойти с равной вероятностью, то они равновозможные.

Если появление события А не сводит к нулю вероятность появление события B, то они совместимые.

Вероятность для суммы таких несовместимых событий состоит из суммы вероятностей каждого из событий:

Если наступление одного события делает невозможным наступление другого, то их называют противоположными. Тогда одно из них обозначают как А, а другое – Ā (читается как «не А»). Появление события А означает, что Ā не произошло. Эти два события формируют полную группу с суммой вероятностей, равной 1.

Зависящие события имеют взаимное влияние, уменьшая или увеличивая вероятность друг друга.

Отношения между событиями. Примеры

На примерах гораздо проще понять принципы теории вероятностей и комбинации событий.

Опыт, который будет проводиться, заключается в вытаскивании шариков из ящика, а результата каждого опыта – элементарный исход.

Событие – это один из возможных исходов опыта – красный шар, синий шар, шар с номером шесть и т. д.

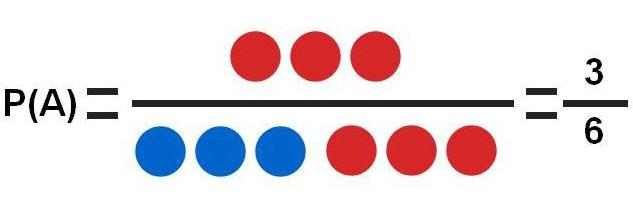
Испытание №1. Участвуют 6 шаров, три из которых окрашены в синий цвет, на них нанесены нечетные цифры, а три других – красные с четными цифрами.

Испытание №2. Участвуют 6 шаров синего цвета с цифрами от одного до шести.

Исходя из этого примера, можно назвать комбинации:

Видно, что первое событие существенно влияет на вероятность второго (40% и 60%).

Формула вероятности события

Переход от гадательных размышлений к точным данным происходит посредством перевода темы в математическую плоскость. То есть суждения о случайном событии вроде «большая вероятность» или «минимальная вероятность» можно перевести к конкретным числовым данным. Такой материал уже допустимо оценивать, сравнивать и вводить в более сложные расчеты.

С точки зрения расчета, определение вероятности события – это отношение количества элементарных положительных исходов к количеству всех возможных исходов опыта относительно определенного события. Обозначается вероятность через Р(А), где Р означает слово «probabilite», что с французского переводится как «вероятность».

Итак, формула вероятности события:

Где m – количество благоприятных исходов для события А, n – сумма всех исходов, возможных для этого опыта. При этом вероятность события всегда лежит между 0 и 1:

Расчет вероятности события. Пример

Возьмем исп. №1 с шарами, которое описано ранее: 3 синих шара с цифрами 1/3/5 и 3 красных с цифрами 2/4/6.

На основании этого испытания можно рассматривать несколько разных задач:

Как видно из расчетов, событие С имеет большую вероятность, поскольку количество вероятных положительных исходов выше, чем в А и В.

Несовместные события

Такие события не могут одновременно появиться в одном и том же опыте. Как в исп. №1 невозможно одновременно достать синий и красный шар. То есть можно достать либо синий, либо красный шар. Точно так же в игральной кости не могут одновременно появиться четное и нечетное число.

Вероятность двух событий рассматривается как вероятность их суммы или произведения. Суммой таких событий А+В считается такое событие, которое состоит в появлении события А или В, а произведение их АВ – в появлении обоих. Например, появление двух шестерок сразу на гранях двух кубиков в одном броске.

Сумма нескольких событий являет собой событие, предполагающее появление, по крайней мере, одного из них. Произведение нескольких событий – это совместное появление их всех.

В теории вероятности, как правило, употребление союза «и» обозначает сумму, союза «или» – умножение. Формулы с примерами помогут понять логику сложения и умножения в теории вероятностей.

Вероятность суммы несовместных событий

Если рассматривается вероятность несовместных событий, то вероятность суммы событий равна сложению их вероятностей:

Например: вычислим вероятность того, что в исп. №1 с синими и красными шарами выпадет число между 1 и 4. Рассчитаем не в одно действие, а суммой вероятностей элементарных составляющих. Итак, в таком опыте всего 6 шаров или 6 всех возможных исходов. Цифры, которые удовлетворяют условие, – 2 и 3. Вероятность выпадения цифры 2 составляет 1/6, вероятность цифра 3 также 1/6. Вероятность того, что выпадет цифра между 1 и 4 равна:

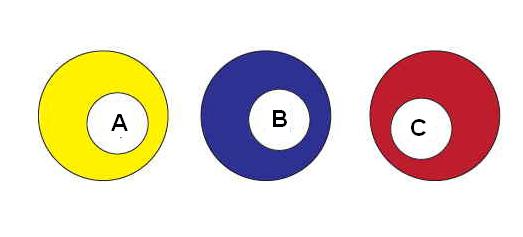
Вероятность суммы несовместимых событий полной группы равна 1.

Так, если в опыте с кубиком сложить вероятности выпадения всех цифр, то в результате получим единицу.

Также это справедливо для противоположных событий, например в опыте с монетой, где одна ее сторона – это событие А, а другая – противоположное событие Ā, как известно,

Вероятность произведения несовместных событий

Умножение вероятностей применяют, когда рассматривают появление двух и более несовместных событий в одном наблюдении. Вероятность того, что в нем появятся события A и B одновременно, равна произведению их вероятностей, или:

Например, вероятность того, что в исп. №1 в результате двух попыток два раза появится синий шар, равна

То есть вероятность наступления события, когда в результате двух попыток с извлечением шаров будет извлечены только синие шары, равна 25%. Очень легко проделать практические эксперименты этой задачи и увидеть, так ли это на самом деле.

Совместные события

События считаются совместными, когда появление одного из них может совпасть с появлением другого. Несмотря на то что они совместные, рассматривается вероятность независимых событий. К примеру, бросание двух игральных костей может дать результат, когда на обеих из них выпадает цифра 6. Хотя события совпали и появились одновременно, они независимы друг от друга – могла выпасть всего одна шестерка, вторая кость на нее влияния не имеет.

Вероятность совместных событий рассматривают как вероятность их суммы.

Вероятность суммы совместных событий. Пример

Вероятность суммы событий А и В, которые по отношению к друг другу совместные, равняется сумме вероятностей события за вычетом вероятности их произведения (то есть их совместного осуществления):

Допустим, что вероятность попадания в мишень одним выстрелом равна 0,4. Тогда событие А – попадание в мишень в первой попытке, В – во второй. Эти события совместные, поскольку не исключено, что можно поразить мишень и с первого, и со второго выстрела. Но события не являются зависимыми. Какова вероятность наступления события поражения мишени с двух выстрелов (хотя бы с одного)? Согласно формуле:

Ответ на вопрос следующий: «Вероятность попасть в цель с двух выстрелов равна 64%».

Эта формула вероятности события может быть применима и к несовместным событиям, где вероятность совместно появления события Р(АВ) = 0. Это значит, что вероятность суммы несовместных событий можно считать частным случаем предложенной формулы.

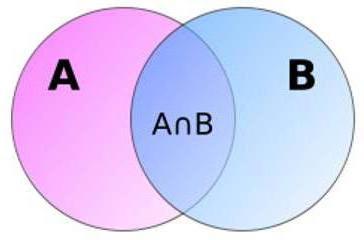
Геометрия вероятности для наглядности

Интересно, что вероятность суммы совместных событий может быть представлена в виде двух областей А и В, которые пересекаются между собой. Как видно из картинки, площадь их объединения равна общей площади за минусом области их пересечения. Это геометрическое пояснения делают более понятной нелогичную на первый взгляд формулу. Отметим, что геометрические решения – не редкость в теории вероятностей.

Определение вероятности суммы множества (больше двух) совместных событий довольно громоздкое. Чтобы вычислить ее, нужно воспользоваться формулами, которые предусмотрены для этих случаев.

Зависимые события

Но ведь событие А тоже случайно, поэтому у него также есть вероятность, которую нужно и можно учитывать в осуществляемых расчетах. Далее на примере будет показано, как работать с зависимыми событиями и гипотезой.

Пример расчета вероятности зависимых событий

Хорошим примером для расчета зависимых событий может стать стандартная колода карт.

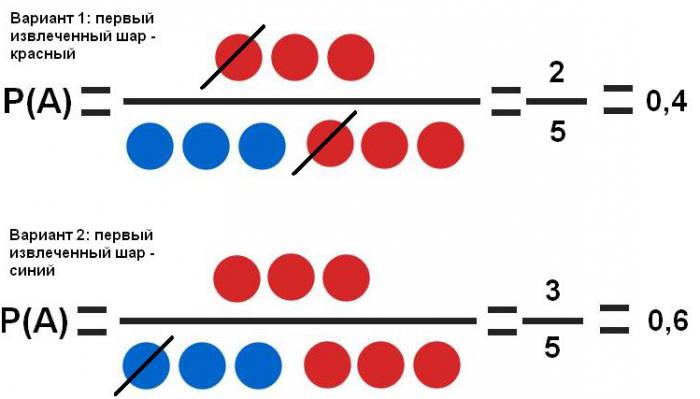
На примере колоды в 36 карт рассмотрим зависимые события. Нужно определить вероятность того, что вторая карта, извлеченная из колоды, будет бубновой масти, если первая извлеченная:

Очевидно, что вероятность второго события В зависит от первого А. Так, если справедлив первый вариант, что в колоде стало на 1 карту (35) и на 1 бубну (8) меньше, вероятность события В:

Если же справедлив второй вариант, то в колоде стало 35 карт, и по-прежнему сохранилось полное число бубен (9), тогда вероятность следующего события В:

Видно, что если событие А условлено в том, что первая карта – бубна, то вероятность события В уменьшается, и наоборот.

Умножение зависимых событий

Руководствуясь предыдущей главой, мы принимаем первое событие (А) как факт, но если говорить по сути, оно имеет случайный характер. Вероятность этого события, а именно извлечение бубны из колоды карт, равна:

Поскольку теория не существует сама по себе, а призвана служить в практических целях, то справедливо отметить, что чаще всего нужна вероятность произведения зависимых событий.

Согласно теореме о произведении вероятностей зависимых событий, вероятность появления совместно зависимых событий А и В равна вероятности одного события А, умноженная на условную вероятность события В (зависимого от А):

Тогда в примере с колодой вероятность извлечения двух карт с мастью бубны равна:

9/36*8/35=0,0571, или 5,7%

И вероятность извлечения вначале не бубны, а потом бубны, равна:

Видно, что вероятность появления события В больше при условии, что первой извлекается карта масти, отличной от бубны. Такой результат вполне логичный и понятный.

Полная вероятность события

Итак, формула полной вероятности для события В при полной группе случайных событий А1,А2,…,А_n равна_:

Взгляд в будущее

Вероятность случайного события крайне необходима во многих сферах науки: эконометрике, статистике, в физике и т. д. Поскольку некоторые процессы невозможно описать детерминировано, так как они сами имеют вероятностный характер, необходимы особые методы работы. Теория вероятности события может быть использована в любой технологичной сфере как способ определить возможность ошибки или неисправности.

Можно сказать, что, узнавая вероятность, мы некоторым образом делаем теоретический шаг в будущее, разглядывая его через призму формул.

Источник