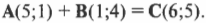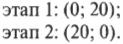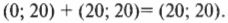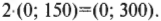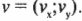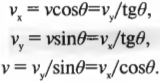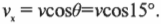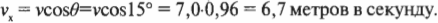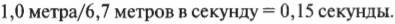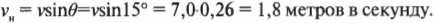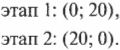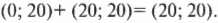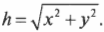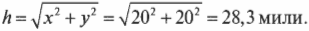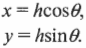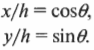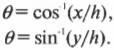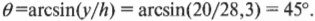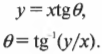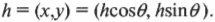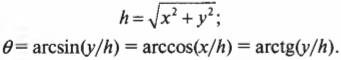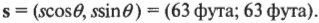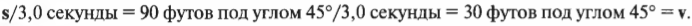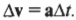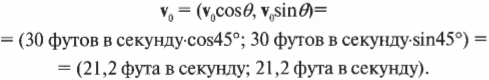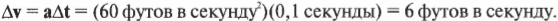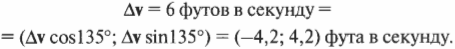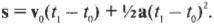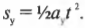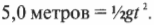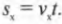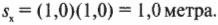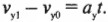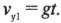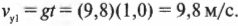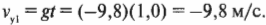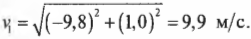Что можно сказать о направлении двух равных векторов
Что можно сказать о направлении двух равных векторов
Сформулируем ряд базовых определений.
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или на параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны.
то есть модуль вектора равен корню квадратному из суммы квадратов его координат.
Обозначим углы между вектором и осями координат через α, β, γ соответственно. Косинусы этих углов называются для вектора 
направляющими, и для них выполняется соотношение: 
Верность данного равенства можно показать с помощью свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем пункте 4.
Пусть в трехмерном пространстве заданы векторы 
своими координатами. Имеют место следующие операции над ними: линейные (сложение, вычитание, умножение на число и проектирование вектора на ось или другой вектор); не линейные – различные произведения векторов (скалярное, векторное, смешанное).
1. Сложение двух векторов производится покоординатно, то есть если
Геометрически два вектора складываются по двум правилам:
а) правило треугольника – результирующий вектор суммы двух векторов соединяет начало первого из них с концом второго при условии, что начало второго совпадает с концом первого вектора; для суммы векторов – результирующий вектор суммы соединяет начало первого из них с концом последнего вектора-слагаемого при условии, что начало последующего слагаемого совпадает с концом предыдущего;
б) правило параллелограмма (для двух векторов) – параллелограмм строится на векторах-слагаемых как на сторонах, приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой векторов.
Геометрически два вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов является диагональ, соединяющая концы векторов, причем результирующий вектор направлен из конца вычитаемого в конец уменьшаемого вектора.
При λ>0 – вектор 
сонаправлен ; λ противоположно направлен ; | λ|> 1 – длина вектора увеличивается в λ раз; | λ| 1 – длина вектора уменьшается в λ раз.
4. Пусть в пространстве задана направленная прямая (ось l ), вектор 
задан координатами конца и начала. Обозначим проекции точек A и B на ось l соответственно через A ’ и B ’.
Рассмотрим некоторые основные свойства проекций:
1) проекция вектора на ось l равна произведению модуля вектора на косинус угла между вектором и осью, то есть 
;
2.) проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой;
3) проекция суммы нескольких векторов на одну и ту же ось равна сумме проекций на эту ось.
Сформулируем определения и теоремы о произведениях векторов, представляющих нелинейные операции над векторами.
5. Скалярным произведением 
векторов и 
называется число (скаляр), равное произведению длин этих векторов на косинус угла φ между ними, то есть
Теорема 2.2. Необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю их скалярного произведения 
Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть 
Отсюда следует условие перпендикулярности ненулевых векторов и :
С помощью скалярного произведения векторов находят работу постоянной силы 
на прямолинейном участке пути.
Решение. Вычислим модули векторов и их скалярное произведение по теореме (2.3):
Пример 2.10. Затраты сырьевых и материальных ресурсов, используемых на производство одной тонны творога, заданы в таблице 2.2 (руб.).
Какова общая цена этих ресурсов, затрачиваемых на изготовление одной тонны творога?
Примечание. Действия с векторами, осуществленные в примере 2.10, можно выполнить на персональном компьютере. Для нахождения скалярного произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве аргументов указываются адреса диапазонов элементов матриц, сумму произведений которых необходимо найти. В MathCAD скалярное произведение двух векторов выполняется при помощи соответствующего оператора панели инструментов Matrix 
Решение. Находим вектор перемещения, вычитая из координат его конца координаты начала
Угол φ между и 
находим по формуле (2.29), то есть
– 
перпендикулярен векторам и ;
– векторы 
образуют правую тройку (рис. 2.15).
Примечание. Определитель (2.25) раскладывается по свойству 7 определителей
Следствие 1. Необходимым и достаточным условием коллинеарности двух векторов является пропорциональность их соответствующих координат
Следствие 2. Векторные произведения единичных орт равны 
Следствие 3. Векторный квадрат любого вектора равен нулю
Также с помощью векторного произведения можно определить момент силы относительно точки и линейную скорость вращения.
— перпендикулярен плоскости, проходящей через точки O , A , B ;
Следовательно, момент силы относительно точки O представляет собой векторное произведение
Решение. Найдем векторное произведение заданных векторов по формуле (2.32).
Теорема 2.6. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения
Теорема 2.7. Если три вектора 
заданы своими координатами, то их смешанное произведение представляет собой определитель третьего порядка, составленный из координат векторов- сомножителей соответственно, то есть
Объем треугольной пирамиды, построенной на этих же векторах, равен
Решение. Найдем координаты векторов
По формуле (2.36) объем пирамиды, построенной на векторах 
равен 
(единиц объема)
Рассмотрим очень важный вопрос о разложении вектора по базису. Приведем следующие определения.
получим выражение вектора 
через остальные векторы 
Линейно независимыми называют векторы, если равенство (2.37) выполняется только тогда, когда все
Базисом n – мерного пространства En называют любую совокупность линейно независимых векторов n – мерного пространства.
Произвольный вектор 
n – мерного пространства можно представить в виде линейной комбинации векторов базиса таким образом:
Линейное пространство называется конечномерным и имеет размерность n , если в этом пространстве существует система из n линейно независимых векторов (базис) такая, что каждое ее расширение приводит к линейной зависимости системы.
Что можно сказать о направлении двух равных векторов
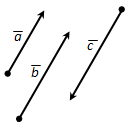
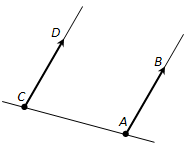
Вопрос 2. Какие векторы называются одинаково направленными (противоположно направленными)?
Ответ. Векторы \(\overline
Векторы \(\overline
На рисунке 212 векторы \(\overline\) и \(\overline\) одинаково направлены, а векторы \(\overline\) и \(\overline
Вопрос 3. Что такое абсолютная величина вектора?
Ответ. Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютная величина вектора \(\overline\) обозначается |\(\overline\)|.
Вопрос 4. Что такое нулевой вектор?
Ответ. Начало вектора может совпадать с его концом. Такой вектор будем называть нулевым вектором. Нулевой вектор обозначается нулём с чёрточкой (\(\overline<0>\)). О направлении нулевого вектора не говорят. Абсолютная величина нулевого вектора считается равной нулю.
Вопрос 5. Какие векторы называются равными?
Ответ. Два вектора называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора.
Вопрос 6. Докажите, что равные векторы одинаково направлены и равны по абсолютной величине. И обратно: одинаково направленные векторы, равные по абсолютной величине, равны.
Ответ. При параллельном переносе вектор сохраняет своё направление, а также свою абсолютную величину. Значит, равные векторы направлены одинаково и равны по абсолютной величине.
Пусть \(\overline
Вопрос 7. Докажите, что от любой точки можно отложить вектор, равный данному вектору, и только один.
Ответ. Пусть CD – прямая, а вектор \(\overline
переводит точку A1 в точку A’1, а точку A2 в точку A’2, т.е. векторы \(\overline
Глава 4. Едем по указателям
Довольно трудно добраться в место назначения — пешком ли, на велосипеде ли, на автомобиле ли, на самолете ли — если вы не знаете направления движения. Для успеха путешествия нужно знать не только расстояние, но и направление движения. В главе 3 описывались такие понятия, как перемещение, скорость и ускорение, связанные некоторыми соотношениями, как, например, \( s=<>^1\!/\!_2at^2+v_0t \) . С помощью таких соотношений можно получить значения для ускорения, например 27 метров в секунду в квадрате, или для скорости, например 42,7 мили в час. Конечно, полезно знать эти параметры движения, но что можно сказать о направлении движения?
В реальном мире просто необходимо знать направление движения. Именно векторы обозначают такое направление. Очень многие люди ошибочно считают векторы очень сложными объектами, но это совсем не так. В этой главе вы узнаете, насколько легко и просто можно обращаться с ними при решении задач.
Осваиваем векторы
В главе 3 мы работали с простыми числами или измерениями, которые в физике называются величинами. Например, в результате измерения перемещения на 3 метра получена величина перемещения 3 метра. Вектор отличается от величины еще и наличием направления. В повседневной жизни на вопрос о пути понятие “вектор” возникает в виде следующего ответа встречного человека: “Это в 15 милях отсюда”. При этом величина вектора равна 15 милям, а направление вектора определяется взмахом руки. Когда вы навешиваете дверь на петли, то порой слышите совет: “Толкните сильнее влево”. Вот вам еще один вектор! Когда вы объезжаете препятствие на дороге, вам приходится ускоряться и замедляться в разных направлениях. Вот еще несколько векторов!
Векторы встречаются в обыденных ситуациях, например в дорожных указателях, инструкциях по сборке или даже при попытке избежать столкновения со встречным. Поскольку физика стоит за всеми событиями повседневной жизни, то не удивительно, что многие физические концепции, например скорость, ускорение, сила, являются векторами. По этой причине следует поближе познакомиться с векторами, поскольку они присутствуют во всех разделах физики. Вектор — это фундаментальное понятие физики.
Определяем направление: основные свойства векторов
При работе с векторами нужно иметь в виду его направление и величину. Физический параметр без направления, а только с величиной называется скаляром. Если к скаляру добавить направление, то получим вектор.
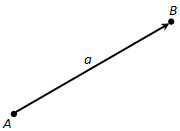
Визуально в физических задачах вектор отображается в виде стрелки. Действительно, стрелка имеет величину (т.е. длину) и направление (т.е. острие). Взгляните на рис. 4.1. Эта стрелка и есть вектор с началом в тупом конце и с окончанием — в заостренном конце.
Допустим, какой-то умник предложит вам дать пример вектора. Проще простого! Достаточно сказать, что у некого вектора А есть некая величина и некоторое направление. Убежден, что это произведет на умника оглушительное впечатление! Например, скажите, что вектор А направлен под углом 15° к горизонтали и имеет величину 12 метров в секунду. Итак, любопытный умник получит исчерпывающую информацию о векторе А.
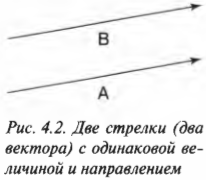
На рис. 4.2 показаны два вектора, А и В. Они очень похожи, поскольку обладают одинаковой длиной и направлением. Фактически оба эти вектора равны. Если два вектора равны по величине и направлению, то они считаются равными, т.е. А = В.
Очень скоро читатель станет настоящим экспертом в области векторов. Уже сейчас нам известно, что, когда мы встречаемся с символом А, это значит, что данный параметр обладает величиной и направлением, т.е. является вектором, а два вектора считаются равными, если они имеют одинаковую величину и направление. Но это еще далеко не все. Допустим, чтобы найти нужный вам отель, нужно проехать 20 миль к северу, а потом 20 миль на восток. Так насколько далеко и в каком направлении находится этот отель?
Комбинируем направления: сложение векторов
Два вектора можно сложить и получить результирующий вектор, который является суммой обоих векторов и определяет расстояние и направление до цели.
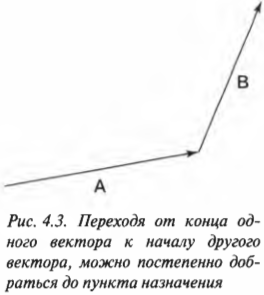
Допустим, что прохожий говорит вам, что для достижения пункта назначения вам нужно сначала следовать вектору А, а потом вектору В. Так где же находится в этом случае ваш пункт назначения? Сначала нужно проехать по пути, указанному вектором А, а потом по пути, указанному вектором В, как показано на рис. 4.3.
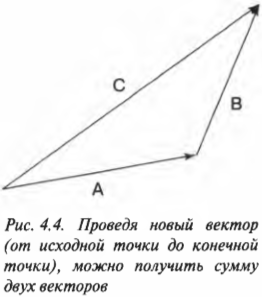
Когда вы доберетесь до конца вектора В, насколько далеко вы будете находиться от исходной точки? Для ответа на этот вопрос начертим еще один вектор С от исходной точки и до конечной точки путешествия, как показано на рис. 4.4.
Новый вектор С представляет собой результат всего путешествия от начала и до самого конца. Все, что нужно сделать, чтобы получить его, так это начертить оба вектора А и В и соединить новым результирующим вектором С.
Сумма векторов достигается за счет того, что начало одного вектора помещается в конец другого, т.е. суммарный вектор проходит от начала одного до конца другого вектора. Иначе говоря, С = А + В. При этом С называется суммой векторов, результатом сложения векторов, или результирующим вектором. Не думайте, что этим ограничиваются возможности комбинирования векторов, ведь векторы можно и вычитать.
Вычисляем разницу расстояний: разность векторов
А что если некто предложит вам векторы С и А, показанные на рис. 4.4, и попросит найти их разность? Их разностью является вектор В, поскольку при сложении векторов А и В получается вектор С. Чтобы объяснить эту мысль, нужно прояснить смысл вычитания вектора А из вектора С: т.е. смысл операции С — А.
Для вычитания двух векторов нужно расположить вместе основания векторов (т.е. концы векторов без остриев), а не совмещать основание одного вектора и острие другого вектора, как при сложении векторов. Затем нужно провести результирующий вектор, который является разностью двух векторов, от острия вычитающего вектора (А) к острию вычитаемого вектора (С). На рис. 4.5 показан пример вычитания вектора А из вектора С (иначе говоря, приведен пример С — А). Как видите, результат такого вычитания равен вектору В, поскольку С = А + В.
Еще один (и для некоторых более простой) способ вычитания векторов заключается в обращении направления второго вектора (т.е. вектора А в разности С — А) и сложении двух векторов: вектора С и обращенного вектора А (т.е. совмещении острия обращенного вектора А с основанием вектора С с последующим проведением результирующего вектора от основания обращенного вектора А к острию вектора С).
Как видите, сложение и вычитание векторов может происходить с одними и теми же векторами в одной задаче. На самом деле с векторами можно выполнять и некоторые другие математические операции. Изложенный выше материал означает, что с векторами можно оперировать так же, как со скалярами, например С = А + В, С — А = В и т.д. Как видите, векторы очень похожи на числа.
Облекаем векторы в числа
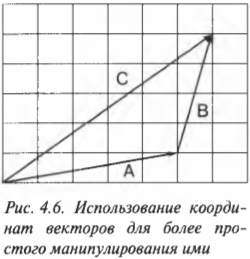
Векторы удобно представлять в виде стрелок, но это не всегда самый точный способ работы с ними. Векторы гораздо точнее можно характеризовать числами. Рассмотрим пример сложения векторов А + В, показанных на рис. 4.6.
Предположим, что измерения на рис. 4.6 даны в метрах. Это значит, что вектор А направлен на 1 метр вверх и на 5 метров вправо, а вектор В направлен на 1 метр вправо и на 4 метра вверх. Для получения параметров результирующего вектора С нужно сложить горизонтальные измерения обоих векторов и отдельно сложить вертикальные измерения обоих векторов.
Результирующий вектор С направлен на 6 метров вправо и на 5 метров вверх. Как видите, для получения вертикального измерения вектора С нужно сложить вертикальное измерение вектора А и вертикальное измерение вектора В. А для получения горизонтального измерения вектора С нужно сложить горизонтальное измерение вектора А и горизонтальное измерение вектора В.
Если процедура сложения векторов все еще очень туманна для вас, то тогда можно использовать другую систему обозначений векторов. Поскольку вектор А “простирается” на 5 метров вправо (в положительном направлении оси X) и на 1 метр вверх (в положительном направлении оси Y), то его можно выразить в координатах (х,у), например А = (5;1). Аналогично, поскольку вектор В “простирается” на 1 метр вверх (в положительном направлении оси X) и на 4 метра вправо (в положительном направлении оси Y), то его можно выразить в координатах (х,у), например В = (1;4).
С помощью такой системы обозначений сложение векторов существенно упрощается. Итак, для сложения двух векторов достаточно сложить их координаты по осям X и Y, чтобы получить координаты результирующего вектора по осям X и Y:
Получается, что весь секрет сложения векторов заключается в разбиении каждого вектора на координаты по осям X и Y с последующим их сложением, чтобы соответственно получить координаты X и Y результирующего вектора? Конечно, работа с этими числами для получения координат X и Y результирующего вектора требует некоторых усилий, но они достаточно просты, чтобы с успехом их выполнить.
Допустим, что нужный вам отель находится на расстоянии 20 миль к северу и на расстоянии 20 миль на восток. Как будет выглядеть вектор, направленный из исходной точки к этому отелю? С помощью координатного представления эта задача решается очень легко. Допустим, что положительное направление оси X направлено на восток, а положительное направление оси Y — на север. На первом этапе нужно проехать 20 миль на север, а на втором этапе — 20 миль на восток. В векторном представлении эта задача формулируется следующим образом (восток [X]; север [Y]):
Чтобы сложить эти два вектора, нужно сложить их координаты по соответствующим осям:
Результирующий вектор, который указывает на отель, имеет вид (20; 20).
Рассмотрим еще один пример удачного применения такого представления векторов. Допустим, что вы едете на гоночном автомобиле со скоростью 150 миль в час на восток и видите в зеркало заднего вида приближающегося соперника. Нет проблем, нужно лишь удвоить скорость:
Теперь вы уже не едете, а почти “летите” со скоростью 300 миль в час, но в том же направлении. Итак, в этой задаче демонстрируется процедура умножения вектора на скаляр.
Разбиение вектора на компоненты
Формулировки задач по физике с использованием векторов не всегда так просты, как предыдущие примеры с манипуляциями векторов. Рассмотрим первый вектор на рис. 4.1 с координатами (4; 1) и сравним его со следующей типичной формулировкой физической задачи: найти время перемещения шара со скоростью 7 метров в секунду по наклонной плоскости с длиной основания 1 м, расположенной под углом 15°. С помощью дальнейшей информации в этом разделе вы научитесь находить компоненты векторов и легко и просто манипулировать ими.
Ищем компоненты вектора по заданной величине и углу
Чтобы определить координаты вектора, нужно научиться разбивать векторы на части, которые называются компонентами. Например для вектора (4; 1) Х-компонентой является число 4, а Y-компонентой — число 1.
Часто в физической задаче задается угол и величина вектора, а его компоненты нужно определить. В предыдущем примере известно, что шар катится со скоростью 7 метров в секунду по наклонной плоскости с длиной основания 1 м, расположенной под углом 15°. Для определения времени перемещения шара от одного конца плоскости к другому нам потребуется разобраться только с Х-компонентой. То есть, задача сводится к определению времени перемещения на расстояние 1 метр вдоль оси X. Для ответа на этот вопрос нужно определить скорость перемещения шара по оси X.
Итак, нам известно, что шар движется со скоростью 7 метров в секунду под углом 15° к горизонтали (т.е. положительного направления оси X). В данной формулировке скорость является вектором \( \mathbf
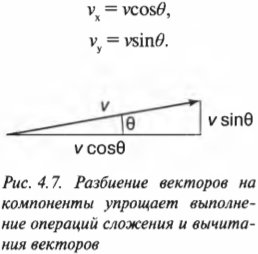
Теперь нам нужно определить Х-компоненту вектора скорости шара, чтобы определить скорость перемещения шара вдоль основания наклонной плоскости. Х-компонента скорости является скаляром (т.е. имеет только значение, а не значение, направление и точку приложения, как вектор) и обозначается как \( v_x \) . Аналогично, Y-компонента скорости шара также является скаляром и обозначается как \( v_y \) . Итак, вектор скорости можно выразить через его компоненты:
Рекомендуется хорошенько запомнить указанные выше выражения для компонент вектора, поскольку нам придется довольно часто встречаться с ними в курсе физики.
Теперь можно пойти немного дальше и попробовать связать отдельные стороны треугольника на рис. 4.7. Это можно легко сделать, если вспомнить соотношение для тангенса \( tg\,\theta=\sin\theta/\cos\theta \) и воспользоваться соотношениями для компонент скорости:
Зная соотношение \( v_x=v\cos\theta \) , можно найти величину Х-компоненты скорости шара \( v_x=v\cos\theta \) :
Подставляя числа, получим
Итак, теперь мы знаем, что горизонтальная скорость шара равна 6,7 метров в секунду. Поскольку длина основания наклонной плоскости равна 1,0 метра, то это расстояние шар преодолеет за время:
Таким образом, благодаря тому, что мы научились определять компоненту скорости, нам удалось легко найти решение все задачи: шару потребуется 0,15 секунды для перемещения вдоль наклонной плоскости. А чему равна Y-компонента скорости? Это можно очень легко определить, поступая аналогично:
Находим величину и направление вектора по его компонентам
Иногда требуется определить угол наклона вектора, если известны его компоненты. Например, предположим, что вы ищите отель, расположенный на 20 миль к северу и на 20 миль к востоку. Под каким углом нужно двигаться к нему и насколько далеко он находится? Условия этой задачи можно записать с помощью уже известных нам векторных обозначений (см. предыдущий раздел):
После сложения этих двух векторов получим следующий результат:
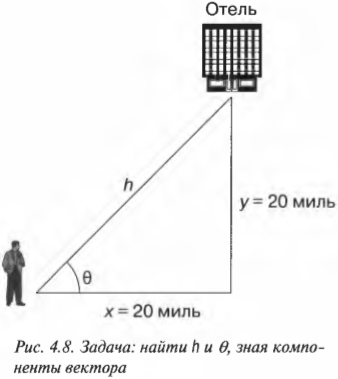
Результирующий вектор, который указывает на отель, имеет вид (20; 20). Это еще один способ указания вектора с помощью его компонент. Итак, вернемся к прежнему вопросу: под каким углом нужно двигаться к отелю и насколько далеко он находится от текущего положения? Иначе говоря, глядя на рис. 4.8, прежний вопрос теперь звучит так: “Чему равны \( h \) и \( \theta \) ?”
Найти \( h \) не так уж и трудно, пользуясь теоремой Пифагора:
Подставляя численные значения, получим:
Итак, отель находится на расстоянии 28,3 мили. А под каким углом \( \theta \) нужно ехать к нему по прямой? Пользуясь основными тригонометрическими соотношениями, можно записать:
Теперь для определения угла нужно использовать функции, обратные синусу и косинусу:
(Строго говоря, обратной синусу функцией является функция “арксинус”, или \( arcsin(x) \) , а обратной косинусу — “арккосинус”, или \( arccos(x) \) . Обозначения \( sin^<-1>(x) \) и \( cos^<-1>(x) \) часто используются для обозначения функций “арксинус” и “арккосинус”, но их не рекомендуется употреблять, чтобы не путать с функциями \( 1/sin(x) \) и \( 1/cos(x) \) . — Примеч. ред.)
Как вычислить значения функций, обратных синусу ( \( sin^ <-1>\) ) и косинусу ( \( cos^ <-1>\) )? Очень просто, ведь в любом инженерном калькуляторе есть кнопки для таких функций! (Например, в программе Калькулятор операционной системы Windows достаточно ввести число, установить флажок параметра Inv (Обратная) и щелкнуть на кнопке sin (Синус). — Примеч. ред.) Достаточно ввести число и нажать соответствующую кнопку, если таковая имеется, например с надписью arcsin (арксинус). В данном случае для угла \( \theta \) получим следующий результат вычислений:
Итак, отель находится на расстоянии 28,3 мили и под углом 45°. Вот так, легко и просто мы успешно решили еще одну физическую задачу!
Аналогично, можно определить угол \( \theta \) без необходимости промежуточного вычисления \( h \) с помощью других сведений из тригонометрии:
(Строго говоря, обратной тангенсу функцией является функция “арктангенс”, или \( arctg(x) \) . Обозначение \( tg^<-1>(x) \) часто используется для обозначения функции “арктангенс”, но его не рекомендуется употреблять, чтобы не путать с функцией \( 1/tg(x) \) . — Примеч. ред.)
Срываем покров с векторов
У нас есть два способа описания векторов для решения физических задач. Первый основан на использовании компонент по осям X и Y, а второй — на величине (модуле) и направлении вектора (угол обычно задается в градусах от 0° до 360°, где угол 0° соответствует направлению вдоль положительного направления оси X). Знание правил взаимного преобразования этих двух способов описания имеет очень большое значение, поскольку для операций с векторами удобно использовать компоненты вектора, а в формулировке физических задач обычно задаются величины и углы векторов.
Вот как выглядит формула преобразования двух способов описания векторов:
В этом уравнении предполагается, что \( \theta \) — это угол между горизонтальной компонентой и гипотенузой \( h \) (т.е. самой длинной стороной прямоугольного треугольника, расположенного напротив прямого угла), как показано на рис. 4.8. Если угол не известен, то его можно вывести, если запомнить, что сумма всех углов треугольника равна 180°, а в прямоугольном треугольнике, если вычесть величину прямого угла 90°, то сумма остальных двух углов равна 90°.
Если вам известны компоненты (х,у), то его величину и направление можно определить по следующим формулам:
Такого рода преобразования нужно уметь легко выполнять, поскольку они довольно часто встречаются в задачах. На этом месте часто многие приходят в растерянность и не могут освоить дальнейший материал именно потому, что не овладели простыми правилами разложения вектора на компоненты.
Перемещение — тоже вектор
Перемещение \( s \) следует обозначать \( \mathbf \) , как вектор с определенной величиной и направлением (для обозначения векторов иногда используют стрелку, которая располагается над именем переменной, например \( \overrightarrow \) ). В реальном мире очень важно знать не только величину, но и направление перемещения.
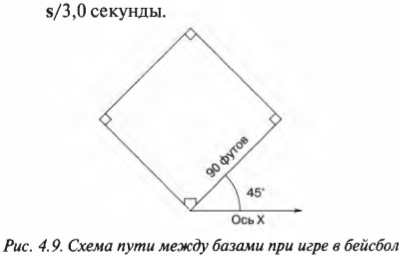
Допустим, что сбылись ваши детские мечты и вы стали звездой бейсбола. Вот вам нужно стремглав бежать к первой базе на расстоянии 90 футов по прямой. Но в каком направлении находится первая база? Допустим, что она находится под углом 45°, как показано на рис. 4.9. Тогда вектор вашего перемещения \( \mathbf \) имеет величину 90 футов и направление 45°. А какими будут компоненты этого вектора? Это очень просто:
Скорость — еще один вектор
Представьте себе, что вы бежите к первой базе с вектором перемещения s с величиной 90 футов и направлением 45° по отношению к оси X. Тут стоило бы задаться вопросом: “Позволит мне моя скорость опередить игрока на первой базе?” Хороший вопрос. Достанем калькулятор и подсчитаем скорость, если известно, что для достижения первой базы вам требуется 3 секунды. Для определения скорости нужно поделить величину вектора \( \mathbf \) на это время:
В этом выражении вектор перемещения делится на скаляр времени. Результатом такого деления является тоже вектор, а именно вектор скорости:
Допустим, что после этих вычислений вы пришли к выводу, что такой скорости недостаточно, чтобы опередить соперника. Ну что ж, нужно срочно изменить направление!
Ускорение — еще один вектор
Что произойдет, если в процессе движения внезапно изменить направление? Вы сразу же почувствуете изменение скорости, а значит, ощутите ускорение. Как и скорость, ускорение \( \mathbf \) является вектором.
Предположим, что в предыдущем примере нужно изменить скорость Y-компоненты скорости до величины 25 футов в секунду, чтобы избежать встречи с соперником, причем вам известно, что вы способны отклониться от курса на 90° с ускорением 60 футов в секунду в квадрате (в отчаянной попытке увильнуть от соперника). Достаточно ли этого ускорения для изменения скорости за ту долю секунды, которая отделяет вас от встречи с соперником?
Разница конечного \( t_1 \) и начального \( t_0 \) момента времени равняется изменению времени \( \Delta t \) . Теперь изменение скорости легко найти по следующей формуле:
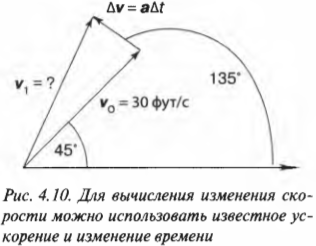
Теперь попробуем вычислить изменение скорости от исходной скорости на основе данных на рис. 4.10.
Для поиска конечного значения скорости \( \mathbf
Теперь остается только выполнить сложение векторов для поиска конечной скорости:
Итак, получен результат \( \mathbf
Именно так нужно работать с векторами разных физических параметров: перемещения, скорости и ускорения. Теперь, обладая такими знаниями, можно перевести скалярные уравнения из главы 3 в векторную форму, например, вот так:
Обратите внимание, что полный вектор перемещения — это комбинация перемещения с начальной скоростью и перемещения с постоянным ускорением.
Упражнение со скоростью: скользим по радуге
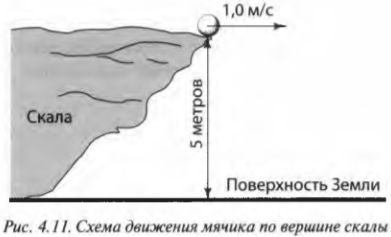
Хотя сила гравитации подробно описывается в главе 6, но здесь мы рассмотрим результат действия этой силы на небольшом примере с векторами в двух измерениях. Представьте себе, что мячик для игры в гольф движется по горизонтальной вершине скалы со скоростью 1,0 м/с и вскоре сорвется с края скалы на высоте 5 метров от поверхности Земли, как показано на рис. 4.11. Насколько далеко улетит мячик и с какой скоростью он столкнется с поверхностью Земли? В этой задаче прежде всего нужно определить время движения мячика.
Итак, как определить, насколько далеко он упадет от края скалы? Один из способов решения этой задачи основан на определении времени движения мячика до столкновения с поверхностью Земли. Поскольку мячик ускоряется только в направлении оси Y (т.е. вертикально вниз), а его компонента скорости по оси X, \( v_x \) , не меняется, то пройденное по горизонтали расстояние до столкновения будет равно \( v_xt \) , где \( t \) — время движения мячика до столкновения. Сила тяготения ускоряет мячик по вертикали, а значит, перемещение по вертикали (т.е. вдоль оси Y) равно:
Это значит, что время движения мячика до столкновения равно:
Итак, мы вычислили, что мячик будет находиться в полете 1,0 секунды. Отлично, явный прогресс! Поскольку компонента скорости мячика по оси X не изменялась в течение этого времени, то можно легко вычислить расстояние, которое пролетит мячик по горизонтали (т.е. вдоль оси X) за это время:
Подставляем числа и получаем:
Итак, мячик столкнется с поверхностью Земли на расстоянии 1,0 метра по горизонтали.
Подставляем числа и получаем:
Триумфальный финал! Мячик пролетит 1,0 метра по горизонтали и столкнется с поверхностью Земли со скоростью 9,9 м/с. Совсем неплохо для начала.