Что можно сделать с помощью циркуля

Построения с помощью циркуля и линейки

Построения с помощью циркуля и линейки — раздел евклидовой геометрии, известный с античных времён.

В задачах на построение возможны следующие операции:

При этом циркуль и линейка считаются идеальными инструментами, в частности

Содержание

Простой пример

Задача. С помощью циркуля и линейки разбить данный отрезок AB на две равные части. Одно из решений показано на рисунке:

Правильные многоугольники

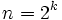
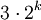
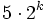
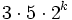
Античным геометрам были известны способы построения правильных n-угольников для , , и .

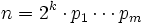
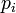
Гаусс показал в 1796 возможность построения правильных n-угольников при , где — различные простые числа Ферма. В 1836 П. Ванцель доказал, что других правильных многоугольников, которые можно построить циркулем и линейкой, не существует.

Известные задачи

Неразрешимые задачи

Следующие три задачи на построение были поставлены ещё в античности:

Только в XIX веке было доказано, что все три задачи не имеют решения. Вопрос возможности построения полностью решён алгебраическими методами, основанными на теории Галуа.

Возможные и невозможные построения

Все построения являются ничем иным, как решениями какого-либо уравнения, причем коэффициенты этого уравнения связаны с длинами заданных отрезков. Поэтому удобно говорить о построении числа — графического решения уравнения определенного типа. В рамках вышеописанных требований, возможны следующие построения:

Иначе говоря, возможно построить лишь числа равные арифметическим выражениям с использованием квадратного корня из исходных чисел (длин отрезков). Например,

Вариации и обобщения

Забавные факты

См.также

Литература

Полезное

Смотреть что такое «Построения с помощью циркуля и линейки» в других словарях:

Построения при помощи циркуля и линейки — Построения с помощью циркуля и линейки раздел евклидовой геометрии, известный с античных времён. В задачах на построение возможны следующие операции: Отметить произвольную точку на плоскости, точку на одной из построенных линий или точку… … Википедия

Построение с помощью циркуля и линейки — Построения с помощью циркуля и линейки раздел евклидовой геометрии, известный с античных времён. В задачах на построение циркуль и линейка считаются идеальными инструментами, в частности: Линейка не имеет делений и имеет сторону бесконечной … Википедия

геометрические построения — приёмы, позволяющие по графически данным элементам (точкам, прямым, окружностям) найти (построить) с помощью наперёд заданных средств другие элементы, связанные с данными некоторыми условиями. Наиболее известны построения с помощью циркуля и… … Энциклопедический словарь

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ — приемы, позволяющие по графически данным элементам (точкам, прямым, окружностям) найти (построить) с помощью наперед заданных средств другие элементы, связанные с данными некоторыми условиями. Наиболее известны построения с помощью циркуля и… … Большой Энциклопедический словарь

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ — приёмы, позволяющие по графически данным элементам (точкам, прямым, окружностям) найти (построить) с помощью наперёд заданных средств др. элементы, связанные с данными нек рыми условиями. Наиболее известны построения с помощью циркуля и линейки… … Естествознание. Энциклопедический словарь

Геометрические построения — решение некоторых геометрических задач при помощи вспомогательных инструментов (линейка, циркуль и т.п.), которые предполагаются абсолютно точными. В исследованиях по Г. п. выясняется круг задач, разрешимых с помощью заданного набора… … Большая советская энциклопедия

Построение циркулем и линейкой — Построения с помощью циркуля и линейки раздел евклидовой геометрии, известный с античных времён. В задачах на построение возможны следующие операции: Отметить произвольную точку на плоскости, точку на одной из построенных линий или точку… … Википедия

Квадратура круга — Круг и квадрат одинаковой площади Квадратура круга задача, заключающаяся в нахождении построения с помощью циркуля и линейки квадрата, равновеликого по площади данно … Википедия

Удвоение куба — классическая античная задача на построение циркулем и линейкой ребра куба, объём которого вдвое больше объёма заданного куба. Наряду с трисекцией угла и квадратурой круга, является одной из самых известных неразрешимых задач на построения с… … Википедия

Гаусс Карл Фридрих — (Gauß) (1777 1855), немецкий математик, иностранный член корреспондент (1802) и иностранный почетный член (1824) Петербургской АН. Для творчества Гаусса характерна органическая связь между теоретической и прикладной математикой, широта… … Энциклопедический словарь

Источник

Построение с помощью циркуля и линейки — описание, алгоритмы и задачи

Построение с помощью циркуля и линейки – древнейший способ расчета в евклидовой геометрии. Известен со времен Древней Греции. Данная тема изучается в средних и старших классах на уроках геометрии.

Рассмотрим все случаи построения на конкретных примерах.

Построение отрезка, равного данному

Есть отрезок СD. Задача — начертить равнозначный данному отрезок той же величины.

Строится луч, имеющий начало в т. A. Циркуль отмеряет существующий отрезок CD. Циркулем откладывается отрезок, равнозначный первому отрезку, на том же начерченном луче от его начала (A).

Для подобного чертежа ножку с иглой закрепляют в начале луча A, а с помощью части с грифелем проводится дуга до места соприкосновения с лучом. Данную точку можно обозначить т. B.

Отрезок AB будет равнозначен отрезку СD. Задача решена.

Деление отрезка пополам

Имеется отрезок AB.

Сначала следует нарисовать окружность с радиусом больше половины отрезка AB с центром в т. A.

Далее чертится круг с тем же радиусом с серединой в т. B. В местах пересечения окружностей имеем т. C и т. D.

Сквозь эти точки требуется провести прямую линию. Получаем т. E, которая будет серединой отрезка AB.

Построение угла, равного данному

Вблизи угла проводится луч ED. Далее чертится окружность с серединой в т. B. В итоге имеем точки M и N.

Оставив раствор циркуля прежним, рисуют круг с серединой в т. E. В точке соприкосновения имеем т. K.

Поменяв раствор циркуля на длину расстояния между т. M и т. N, нужно провести окружность с серединой в т. K. В итоге получается т. F. После чертится прямая из т. E через т. F. Образуется угол DEF, который будет равнозначен углу ABC. Задача решена.

Построение перпендикулярных прямых

Пример 1

Точка O находится на прямой a.

Есть прямая и точка, находящаяся на ней. Нанести линию, идущую через существующую точку и находящуюся под прямым углом к имеющейся прямой.

Шаг 1. Чертим круг с рандомным радиусом r с серединой в т. O. Окружность соприкасается с прямой в т. A и т. B.

Шаг 2. Из имеющихся точек строится круг с радиусом AB. Точки С и D являются точками соприкосновения окружностей.

Приложив линейку, чертят прямую, сквозь т. O и одну из т. C или т. D, к примеру отрезок OC.

Доказательство, что прямая OC лежит перпендикулярно a.

Намечаются два отрезка — AC и CB. Получившиеся треугольники будут равны, согласно третьему признаку равенства треугольников. Значит, прямая CO перпендикулярна AB.

Пример 2

Точка O находится вне прямой а.

Нарисовать окружность с радиусом r из т. O. Она должна проходить сквозь прямую a. A и B — точки её соприкосновения с прямой.

Оставив прежний радиус, рисуем окружности с серединой в т. A и т. B. Точка O1 — место их соприкосновения.

Рисуем линию, соединяющая т. O и т. O1.

Доказательство выглядит следующим образом.

Две прямые ОО1 и AB пересекаются в т. C. Согласно третьему признаку равенства всех треугольников AOB = BO1A. Из данного вывода следует, что угол OAC = O1AC. Одноименные треугольники также будут равны (согласно первому признаку равенства всех треугольников).

Исходя из этого, выводим, что угол OCA = O1CA, а, учитывая смежность углов, приходим к пониманию, что они прямые. А это означает, что OC – перпендикулярный отрезок, опущенный из т. O на прямую a. Задача решена.

Построение параллельных (непересекающихся) прямых

Имеется прямая и т. А, не лежащая на этой прямой.

Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.

Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.

Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.

C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.

Проводится прямая через т. A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.

Построение правильного треугольника, вписанного в окружность

Правила построения правильного треугольника, вписанного в окружность:

Отметить отрезок AB, чья длина будет равняться а.

Взять циркуль. Часть с иголкой расположить на т. А, а часть с карандашом на т. B. Прочертить окружность. В итоге, радиус круга будет равнозначен длине отрезка AB.

Далее иглу размещают на т. B, а часть с грифелем на т. A. Чертится круг. В итоге, его радиус будет равнозначен длине отрезка AB.

На чертеже окружности пересеклись в двух точках. Далее нужно соединить т. A и т. B и одну из вышеупомянутых точек. В результате получится равносторонний треугольник.

Стороны такого треугольника равнозначны радиусам двух окружностей, которые равны длине а. Задача решена.

Построение правильного четырехугольника вписанного в окружность

Вариант 1

Исходя из данности, что диагонали любого квадрата пересекаются в середине окружности и находятся по отношению к его осям под углом 45 градусов, производят следующие действия. Пользуясь линейкой и уголком с углами 45 градусов (см. рисунок), размечают вершины т. 1 и т. 3.

Сквозь данные точки чертят отрезки, стороны четырехугольника, расположенные по горизонтали. Это т. 4 и т. 1, т. 3 и т. 2. В конце линейкой и уголком по его катету проводятся линии, расположенные по вертикали (высоты), отрезок т.1 — т. 2 и отрезок т. 4 — т. 3.

Вариант 2

Так как вершины правильного четырехугольника разделяют наполовину дуги окружностей, между точками диаметра (см. рисунок), то для достижения результата делают следующее: отмечают на точках перпендикулярных диаметров т. A, т. B и т. C и рисуют дуги до их соприкосновения.

После чертят прямые через места соприкосновения дуг, которые выделены на фигуре линиями. Точки соприкосновения с окружностью будут являться вершинами — это т. 1 и т. 3, т. 4 и т. 2. Данные вершины полученного квадрата соединяют друг с другом.

Задача выполнена двумя способами.

Построение вписанного в окружность правильного пятиугольника

Поместить на окружность т. 1, считая ее за вершину пятиугольника. Разделить отрезок AO пополам. Чтобы произвести подобную операцию, из т. A чертят дугу до места соприкосновения с окружностью в т. M и т. B.

Расположив конкретные точки на прямой, получаем т. K, и после совмещаем с т. 1. Радиусом, длина которого – отрезок А1, сделать изгиб из т. K до места соприкосновения с линией АО в т. H. После совместить т. 1 и т. H, образуя одну из пяти сторон пятиугольника.

Взять циркуль, величина раствора которого будет равна отрезку т.1 — т. H, нарисовать изгиб из т. 1 до соприкосновения с кругом. Так находят вершины 2 и 5. Отметив точки на вершинах 2 и 5, получают вершины 3 и 4. В конце все точки совмещают друг с другом.

Построение правильного шестиугольника, вписанного в окружность

Решение подобной задачи строится на свойствах, где сторона шестиугольника равнозначна радиусу круга.

Для расчета разделяют круг на шесть ровных частей и последовательно совмещают все полученные точки (см. рисунок). Задача решена.

Источник

Проект по математике «Рисование циркулем»

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«СОШ №1» Г.ЖИЗДРЫ КАЛУЖСКОЙ ОБЛАСТИ

Автор: Мурнаева Валентина,

учащаяся 5б класса

Руководитель: Яшина Н.М.,

С детства я очень люблю рисовать. Однажды на уроке математики, когда мы изучали тему «Окружность и круг», нам предложили нарисовать рисунок циркулем. Можно было скопировать рисунки из учебника, можно было придумать свой рисунок. Я очень увлеклась этим занятием и позднее решила этому посвятить свой проект.

Тема моего проекта называется « Рисунки циркулем».

вручную сделать практические и творческие задачи на построение циркулем.

изучить сведения по этому вопросу в школьном учебнике математики,

сделать самостоятельно рисунки циркулем,

найти новые способы создания рисунков с помощью различных источников информации,

сделать мультимедийную презентацию о создании простейшего орнамента циркулем.

Гипотеза: я предположила, что рисование циркулем – это просто и увлекательно и это занятие кому-нибудь нужно.

Начав с копирования рисунка из учебника, я стала, затем придумывать свои и выполнять рисунки в цвете. Мне очень нравился этот процесс. Мне нравилось, что учитель меня хвалит и поддерживает. Затем мы стали усложнять рисунки, придумывая целые композиции, например: животное, цветок, какой-нибудь сюжет, а затем стали придумывать орнаменты. Это было уже непросто, не все получалось. Я стала искать рисунки в интернете, в библиотеке. Оказывается, что существуют целые программы на компьютере, чтобы рисовать циркулем не вручную, а с помощью машины, т.е. техники.

Таким образом, я поняла, что очень сложные и красивые рисунки не так легко создать, что человек позвал на помощь себе машину.

Я узнала, что орнаменты применяются в строительстве, для украшения, в раскраске стекол для различных целей, для раскраски тканей и т.д.

В ходе работы я столкнулась с такими проблемами: во-первых, что в 5 классе не изучается, как с помощью циркуля делить отрезок пополам и многие другие задачи на построение, во-вторых, способы составления рисунка, которые я нашла в интернете, не так легко повторить, надо много времени и терпения, чтобы разобраться.

Мне удалось достичь цели проекта, потому что мне нравится рисовать, мне нравится получать удивительные, красивые композиции и орнаменты. Мне удалось изучить возможности циркуля, этого чудо-устройства.

В моей работе присутствует коллекция лучших рисунков циркулем моих одноклассников. Мне удалось в течение нескольких месяцев заниматься творчеством, создавая необычные рисунки, окрашивать их в различные цветовые гаммы. Не все рисунки получились, какие хотелось бы. Не смотря на это, я получила большое эстетическое удовольствие в процессе выполнения этого проекта. Я также рада, что выбрала такой проект, который соединил мое любимое занятие с математикой.

Совершенствование техник работы с циркулем——————————-18

С детства я очень люблю рисовать. Однажды на уроке математики, когда мы изучали тему «Окружность и круг», нам предложили нарисовать рисунок циркулем. Можно было скопировать рисунки из учебника, можно было придумать свой рисунок. Я очень увлеклась этим занятием и позднее решила этому посвятить свой проект.

Тема моего проекта называется « Рисунки циркулем».

вручную сделать практические и творческие задачи на построение циркулем.

изучить сведения по этому вопросу в школьном учебнике математики,

сделать самостоятельно рисунки циркулем,

найти новые способы создания рисунков с помощью различных источников информации,

сделать мультимедийную презентацию о создании простейшего орнамента циркулем.

Гипотеза: я предположила, что рисование циркулем – это просто и увлекательно и это занятие кому-нибудь нужно.

Циркуль делается из металла и состоит из двух частей, соединённых шарниром. Обычно на конце одной из них располагается игла, на конце другой — пишущий предмет, например грифель карандаша, рейсфедер или специальный держатель для рапидографа. У измерительного циркуля иглы на обеих ножках.

Циркуль изобрёл очень талантливый юноша, который придумал гончарный круг, первую в мире пилу. Под пеплом Помпеи археологи обнаружили много таких предметов, изготовленных из бронзы. В нашей стране впервые обнаружены в Нижнем Новгороде. Писатель Ю.Олеша писал: «В бархате лежит, плотно сжав ноги, холодный и сверкающий. У него тяжёлая голова. Я намереваюсь поднять его, он неожиданно раскрывается и производит укол в руку ».

Я поразилась очень красивым узорам в кругах. Оказывается, что они нарисованы при помощи циркуля. Сначала легонько рисуются лепестки (сколько нужно), а потом это обводится фломастерами или красками. Круговой орнамент. Как рисовать циркулем?

Я разработала простую пошаговую инструкцию кругового орнамента.

Я узнала, что орнаменты применяются в строительстве, для украшения, в раскраске стекол для различных целей, для раскраски тканей и т.д.

Пошаговая инструкция «Орнамент с помощью циркуля ».

3. Из этой точки проводим циркулем внутри круга (линия должна пройти через центр круга)

4. Втыкаем циркуль в новое место пересечения

5. Опять рисуем часть окружности

6. Продолжаем, и вот он –первый лепесток.

7. Рисуем круги из всех точек пересечения, и получаем цветок

9. Больше повторов – больше красоты!

10. Можно ограничить область рисования дополнительным кружочком

В процессе может понадобиться транспортир, чтобы найти промежуточные точки на окружности. Первоначальный цветок состоит из 6-ти лепестков. Значит, угол между лепестками равен 360 / 6 = 60 градусов. Красиво начинать от дополнительных точек под кратными углами. Например, 15, 30, 45, 60°. Или 20, 40, 60°. Можно обойтись только циркулем, если умеешь находить середину отрезка: Делим отрезок пополам с помощью циркуля.

Делим отрезок пополам с помощью циркуля:

• Из концов отрезка рисуем две одинаковые окружности

• Проводим прямую через их пересечение.

Начав с копирования рисунка из учебника, я стала, затем придумывать свои и выполнять рисунки в цвете.

Мне очень нравился этот процесс. Мне нравилось, что учитель меня хвалит и поддерживает. Затем мы стали усложнять рисунки, придумывая целые композиции, например: животное, цветок, какой-нибудь сюжет, а затем стали придумывать орнаменты. Это было уже непросто, не все получалось. Я стала искать рисунки в интернете, в библиотеке.

Удивительный по красоте цветок можно нарисовать при помощи циркуля, а затем заполнить цветом, если захочется. С чего следует начинать? Для начала нужно сходить в магазин, чтобы купить циркуль, альбом или ватман. Для раскрашивания пригодится все, чем можно раскрашивать: краски, мелки, карандаши или фломастеры.

Нарисуем циркулем окружность (я буду называть ее центральной). Сохраняя этот радиус, поставим острие циркуля на полученную окружность в любом месте и нарисуем еще одну окружность. Двигаясь по часовой стрелке, установим острие циркуля в точке пересечения последней окружности с центральной и начертим еще одну окружность. Снова поставим острие в точку пересечения предыдущей окружности с центральной и проведите окружность. Двигаясь таким образом, мы получим окружность с шестью окружностями-лепестками. Теперь опустим перпендикуляр из точки пересечения двух окружностей-лепестков на отрезок, соединяющий две соседние точки пересечения окружностей-лепестков с основной окружностью. Если есть линейка, просто можно измерить расстояние между этими точками и отметить середину отрезка. Перпендикуляр из этой точки пересечет основную окружность в точке, куда нужно установить острие циркуля и провести окружность. Затем, двигаясь по часовой стрелке, как и в первом круге окружностей, нужно начертить еще шесть. В конечном итоге у нас получится цветок с двенадцатью лепестками-окружностями.

Сказать, что рисование оного – завораживающий процесс, значит, вообще ничего не сказать.

Рисование яблока циркулем

На этом возможности циркуля не заканчиваются. После этого с помощью циркуля можно нарисовать яблоко. Этот способ я нашла в интернете. Кажется, что «Это очень просто»! Но это не так.

Я ни один раз, начинала этот процесс заново. Но когда я смола нарисовать свое яблоко, моему восторгу не было предела. Хотя сам процесс рисования не сложный, но захватывающий, т.к. грифель циркуля, рисуя все новые окружности, преображает рисунок в затейливые формы.

Я узнала, что орнаменты применяются в строительстве, для украшения, в раскраске стекол для различных целей, для раскраски тканей и т.д.

В ходе работы я столкнулась с такими проблемами: во-первых, что в 5 классе не изучается, как с помощью циркуля делить отрезок пополам и многие другие задачи на построение, во-вторых, способы составления рисунка, которые я нашла в интернете, не так легко повторить, надо много времени и терпения, чтобы разобраться.

Мне удалось достичь цели проекта, потому что мне нравится рисовать, мне нравится получать удивительные, красивые композиции и орнаменты. Мне удалось изучить возможности циркуля, этого чудо-устройства.

В моей работе присутствует коллекция лучших рисунков циркулем моих одноклассников. Мне удалось в течение нескольких месяцев заниматься творчеством, создавая необычные рисунки, окрашивать их в различные цветовые гаммы. Не все рисунки получились, какие хотелось бы. Не смотря на это, я получила большое эстетическое удовольствие в процессе выполнения этого проекта. Я также рада, что выбрала такой проект, который соединил мое любимое занятие с математикой.

Я вручную сделала то, что сейчас обычно рассчитывается на компьютере.

Оказывается, что существуют целые программы на компьютере, чтобы рисовать циркулем не вручную, а с помощью машины, т.е. техники.

Таким образом, я поняла, что очень сложные и красивые рисунки не так легко создать, что человек позвал на помощь себе машину.

В каком-то смысле я воскресила древнюю практику. Моя мотивация – творческое самовыражение и самопознание – сравнима с мотивацией древних ученых, которые считали линии, углы и числа проявлением божественного». По-моему, мое творчество – это отличная возможность увидеть в себе нечто новое через призму древних знаний.

Источник