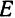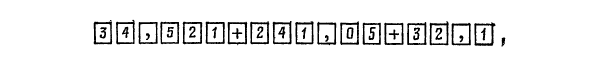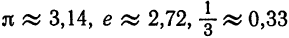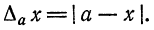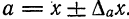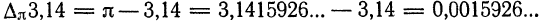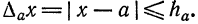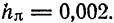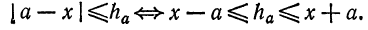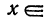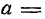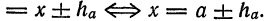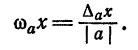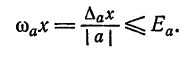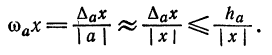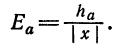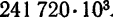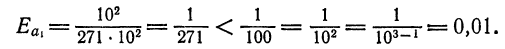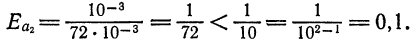Что изучает вычислительная математика

ВЫЧИСЛИ́ТЕЛЬНАЯ МАТЕМА́ТИКА

Том 6. Москва, 2006, стр. 155-156

Скопировать библиографическую ссылку:

ВЫЧИСЛИ́ТЕЛЬНАЯ МАТЕМА́ТИКА, раз­дел ма­те­ма­ти­ки, вклю­чаю­щий круг во­п­ро­сов, свя­зан­ных с ис­поль­зо­ва­ни­ем элек­трон­но-вы­чис­лит. ма­шин (ЭВМ, ком­пью­те­ров). Со­дер­жа­ние тер­ми­на «В. м.» нель­зя счи­тать ус­та­но­вив­шим­ся, т. к. эта об­ласть ма­те­ма­ти­ки ин­тен­сив­но раз­ви­ва­ет­ся в свя­зи с со­вер­шен­ст­во­ва­ни­ем вы­чис­лит. тех­ни­ки и при­ме­не­ния­ми ЭВМ в но­вых на­прав­ле­ни­ях. На на­чаль­ном эта­пе ис­поль­зо­ва­ния ЭВМ тер­мин «В. м.» по­ни­мал­ся как тео­рия чис­лен­ных ме­то­дов и ал­го­рит­мов ре­ше­ния ти­по­вых ма­те­ма­тич. за­дач. Впо­след­ст­вии тер­мин «В. м.» стал по­ни­мать­ся в ука­зан­ном вы­ше бо­лее ши­ро­ком смыс­ле. В В. м. мож­но вы­де­лить сле­дую­щие три осн. раз­де­ла. Пер­вый свя­зан с при­ме­не­ни­ем ЭВМ в разл. об­лас­тях на­уч­ной и прак­тич. дея­тель­но­сти и мо­жет быть ха­рак­те­ри­зо­ван как по­строе­ние и ана­лиз ма­те­ма­тич. мо­де­лей. Вто­рой свя­зан с раз­ра­бот­кой ме­то­дов и ал­го­рит­мов ре­ше­ния ти­по­вых ма­те­ма­тич. за­дач, воз­ни­каю­щих при ис­сле­до­ва­нии ма­те­ма­тич. мо­де­лей. Тре­тий раз­дел свя­зан с во­про­сом об уп­ро­ще­нии взаи­мо­отно­ше­ний че­ло­ве­ка с ЭВМ. Боль­шой вклад в раз­ви­тие В. м. внес­ли Н. С. Бахва­лов­, В. В. Вое­во­дин, В. М. Глуш­ков, С. К. Году­нов­, А. А. Дород­ни­цын­, А. П. Ершов­, Ю. И. Журав­лёв­, М. В. Келдыш­, М. М. Лавренть­ев­, Г. И. Марчук­, Н. Н. Мои­се­ев, А. Н. Тихо­нов­, А. А. Са­мар­ский.

Источник

Вычислительная математика

Вычислительная математика — раздел математики, включающий круг вопросов, связанных с производством разнообразных вычислений. В более узком понимании вычислительная математика — теория численных методов решения типовых математических задач. Современная вычислительная математика включает в круг своих проблем изучение особенностей вычисления с применением компьютеров.

Вычислительная математика обладает широким кругом прикладных применений для проведения научных и инженерных расчётов. На её основе в последнее десятилетие образовались такие новые области естественных наук, как вычислительная химия, вычислительная биология и так далее.

Содержание

История

Вычислительная математика возникла довольно давно. Ещё в Месопотамии были разработаны методы получения квадратного корня. В эпоху научной революции вычислительная математика развивалась быстрыми темпами из практических применений параллельно с математическим анализом. Помимо этого, подобные вычисления широко применялись в небесной механике для предсказания траектории движения небесных тел. Это привело к появлению таких важнейших составляющих физики, как теория о гелиоцентрической системе устройства мира, законы Кеплера и законы Ньютона. XVII и XVIII век стали временем разработки значительного количества численных методов и алгоритмов.

Применение большого количества инженерных вычислений в XIX и XX веках потребовало создания соответствующих приборов. Одним из таких приборов стала логарифмическая линейка, также появились таблицы значений функций с точностью до 16 знаков после запятой, помогавшие проводить вычисления. Также существовали механические устройства для выполнения математических операций, называвшиеся арифмометрами. В первой половине XX века для решения дифференциальных уравнений стали активно использоваться аналоговые ЭВМ.

Изобретение компьютера в середине XX века означало создание универсального инструмента для математических вычислений. Совместно с мейнфреймами в распоряжении инженеров и учёных для выполнения ручных операций были только калькуляторы, которые активно использовались вплоть до начала массового производства персональных компьютеров.

Основные направления

Методы и алгоритмы решения типовых математических задач с применением вычислительной техники носят название численных методов. К типовым задачам относят [2] :

Особенности представления чисел в компьютере

Основное отличие вычислительной математики заключается в том, что при решении вычислительных задач человек оперирует машинными числами, которые являются дискретной проекцией вещественных чисел на конкретную архитектуру компьютера. Так например если взять машинное число длиной в 8 байт, то в нём можно запомнить только 2 64 разных чисел, поэтому важную роль в вычислительной математике играют оценки точности алгоритмов и их устойчивость к представлениям машинных чисел в компьютере. Именно поэтому, например, для решения линейной системы алгебраических уравнений очень редко используется вычисление обратной матрицы, так как этот метод может привести к ошибочному решению в случае с сингулярной матрицей, а очень распространённый в линейной алгебре метод, основанный на вычислении определителя матрицы и её дополнения требует гораздо больше арифметических операций, чем любой устойчивый метод решения линейной системы уравнений.

Программное обеспечение

Многие системы компьютерной алгебры, такие как Mathematica, имеют возможность задавать необходимую арифметическую точность, что позволяет получить результаты более высокой точности. Также, большинство электронных таблиц могут быть использованы для решения простых задач вычислительной математики.

Источник

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

Анализ математич. моделей включает в себя изучение постановки задачи, выбор модели, анализ и обработку входной информации, численное решение математич. задач, возникающих при исследовании модели, анализ результатов вычислений и, наконец, вопросы, связанные с реализацией полученных результатов.

Задача выбора модели должна решаться с учетом следующего требования. Степень достоверности, с к-рой результаты анализа модели позволяют исследовать конкретное явление (или класс явлений), должна соответствовать точности исходной информации. При этом с появлением возможности получать более точную информацию обычно возникает необходимость совершенствования построенной модели, а в ряде случаев даже коренной ее замены. Для этих задач приобретает существенное значение обработка исходной информации, что в большинстве случаев требует привлечения методов математич. статистики.

Математич. модели сыграли важную роль в развитии естествознания; в настоящее время использование математич. моделей является существенным фактором в широком диапазоне человеческой деятельности (в том числе в вопросах планирования, управления, прогнозирования и т. д.).

Изучение реальных явлений на основе анализа построенных моделей, как правило, требует развития численных методов и привлечения ЭВМ. Таким образом, в В. м. важное место занимают численные методы решения поставленных математич. задач и в первую очередь типовых математич. задач (В. м. в узком смысле слова).

Быстро развивающимся направлением В. м. являются численные методы оптимизации. Задача оптимизации состоит в изучении экстремальных (наибольших или наименьших) значений функционалов на множествах, как правило, весьма сложной структуры (см., напр., Экстремальные задачи;численные методы решения). В первую очередь следует упомянуть задачи математического программирования (в том числе линейного и динамического), к к-рым сводятся многие задачи экономики. К задачам оптимизации примыкают минимаксные задачи (и соответствующие численные методы), возникающие при решении задач исследования операций (см. Исследование операций).и теории игр (см. Игр теория). Особенно сложные задачи типа minmaxminmax возникают при решении многошаговых (динамически развивающихся) игр. Здесь даже математич. эксперимент (проигрывание вариантов поведения играющих) невозможен без использования мощных ЭВМ.

Обратные задачи, напр, задача определения элемента хиз уравнения Ах=b при известной информации об операторе Аи элементе b, часто являются неустойчивыми (некорректно поставленными) задачами (малым погрешностям во входных данных могут соответствовать большие погрешности в х). Более того, обратные задачи часто имеют решение не для всех b, поэтому, задавая приближенное значение b, следует учитывать, что формально решение этой задачи может не существовать. Неустойчивые задачи потребовали специального определения понятия приближенных решений и развития соответствующих методов для их нахождения. К неустойчивым задачам относится широкий класс задач, связанных с проблемами автоматизации обработки результатов экспериментов (см. Некорректные задачи;численные методы решения).

В большинстве разделов В. м. важное место занимают вопросы оптимизации методов решения задач. Особенно это существенно для задач большого объема (напр., с большим числом переменных).

Применение ЭВМ непрерывно расширяет круг пользователей и поэтому возникает тенденция такой степени автоматизации, при к-рой становится менее существенным знакомство пользователей с численными методами. Это предъявляет новые требования к алгоритмам, их классификации и к стандартным программам решения типовых задач.

В настоящее время выделился ряд направлений прикладной науки, где современные темпы научно-технич. прогресса были бы немыслимы без развития численных методов и применения ЭВМ (см., напр., Газовой динамики численные методы).

Основной задачей теории программирования можно считать облегчение отношений человека с машиной, хотя этот взгляд и конкретные направления исследований претерпевают радикальные изменения с развитием вычислительной техники. Смена ряда поколений вычислительных машин обусловила смену этапов в развитии программирования.

От составления программ на внутреннем языке машин программирование быстро перешло к составлению стандартных программ решения типовых задач и комплексов таких программ. При их употреблении для широкого класса задач отпадает необходимость в программировании метода решения; достаточно лишь ограничиться заданием исходной информации. Однако задание такой информации, а также написание нестандартных блоков все равно требуют существенного объема программирования на языке машины (см. Машинно-ориентированный язык).

Наряду с созданием универсальных алгоритмич. языков (алгол, фортран) был разработан ряд проблемно-ориентированных языков для определенного круга пользователей, цапр. связанных с задачами обработки эко-номич. информации (кобол). Создание специализированных языков вызвано следующим: универсальные языки и трансляторы, предназначенные для решения широкого класса задач, иногда слабо учитывают специфику отдельных важных классов задач, что снижает эффективность использования всех возможностей машины.

Развитие применения ЭВМ характерно также организацией работы комплексов, включающих большое число машин, в том числе машин различных типов, вводные устройства, каналы связи между машинами и пользователем, а зачастую и физич. установки. Такие высокопроизводительные системы создаются, напр., для решения задач экономики и обработки физич. экспериментов, требующих ввода и обработки большого количества информации.

Задача развития вычислительных систем, в частности информационных систем и автоматизированных систем управления, является одной из наиболее актуальных

научных проблем. А. Н. Тихонов.

Источник

Вычислительная математика и её элементы с примерами

Роль математики в современной науке и технике:

С самых древних времен практическая деятельность людей была связана с необходимостью выделения и обозрения тех или иных совокупностей объектов, участков земли, установления их количественных оценок. Во всех этих случаях нужно было представлять совокупности различных элементов как единое целое, определять формы участков земли и сосудов, измерять их площади
и объемы, сравнивать, вычислять.

В результате многолетней практической деятельности людей возникли основные абстрактные математические понятия, такие как понятия множества, отношения, числа, геометрической фигуры. В дальнейшем математика как наука развивалась в тесной связи с развитием производственной деятельности людей и общечеловеческой культуры. За свою многовековую историю
математика превратилась в стройную дедуктивную науку,
предоставляющую мощный аппарат для изучения реального мира,.

Особое значение для развития науки, техники и в целом народного хозяйства приобретает математика в наши дни. Одной из характерных черт современного научно-технического прогресса является существенное расширение областей применения теоретической и вычислительной математики на базе широкого
использования электронных вычислительных машин (ЭВМ). Сейчас математические методы и вычислительная техника широко применяются не только в таких традиционных науках как механика, астрономия, физика,

но и в экономике, химии и даже в таких, с первого взгляда как будто бы далеких от математики отраслей знания, как социология, лингвистика, биология, медицина и др.

Чем объяснить такое широкое проникновение
математики в другие науки? В первую очередь, большинство
направлений научной и технической деятельности людей достигли сравнительно высокого уровня своего развития и, на данном этапе, исчерпали возможности описательных методов исследования. В связи с этим дальнейший успех возможен только на базе использования точных количественных методов исследования, т. е.
применения математического аппарата. Во-вторых, развитие самой математики и ряда смежных научных дисциплин, таких как математическая логика, физика, в особенности электроника, позволило создать мощные электронные вычислительные машины, способные выполнять большие объемы громоздкие массовых
вычислений.

Современные вычислительные машины способствуют не только решению сложных практических задач, которые не могут быть решены в реальном отрезке времени непосредственными человеческими усилиями, но также и дальнейшему развитию теоретических исследований.

Только благодаря высокому уровню развития науки и техники, их влиянию друг на друга и взаимному обогащению, столь характерным для современной научно-технической революции, стало возможным решать такие трудоемкие и сложные задачи, как создание автоматизированных систем управления (АСУ) предприятиями и отраслями производства, оптимальное планирование народного хозяйства, использование атомной энергии в мирных целях, создание пассажирских сверхзвуковых самолетов и крупнейших морских кораблей разного назначения, таких, как ледоколы «Ленин», «Арктика», «Сибирь», изучение космического пространства,
обеспечение длительной работы научных экспедиций в космосу и т. д. В решении таких задач важную роль играет теоретическая и вычислительная математика, и в особенности современная вычислительная техника.

Однако было бы ошибкой думать, что математические методы нужны только для решения крупных задач. При изучении основ естественных наук в средней школе мы встречались с примерами применения математических

методов и вычислений в решении различных конкретных задач. Подобные задачи (как правило, простые, а иногда и довольно сложные) встречаются в ежедневной работе технических специалистов, экономистов, технологов. Поэтому работникам народного хозяйства, в какой бы области они ни трудилсь, необходимо владеть основными математическими методами исследования и приемами вычислений, устным, письменным и инструментальным счетом. Специалисты должны иметь полное представление о возможностях современной универсальной и специализированной вычислительной техники, уметь пользоваться
распространенными вычислительными машинами.

Вычислительные машины и приспособления дискретного и непрерывного действия

Для облегчения вычислений и сохранения результатов счета используются различные вспомогательные средства и приспособления. Одним из древних таких приспособлений являются русские счеты, которые до сих пор с успехом применяются на практике и на которых полезно уметь хорошо считать. Математиками и инженерами создавались и другие, иногда довольно сложные механические вычислительные машины. Однако скорость выполнения вычислений на таких машинах была невелика. Новый этап в развитии вычислительной техники начался в середине нашего века, когда были созданы первые электронные вычислительные машины. В электронных вычислительных машинах механическое движение деталей сведено к минимуму, оно заменено передачей электрических импульсов, вследствие чего существенно повысилась скорость вычислений. За прошедшие несколько десятилетий в создании вычислительной техники были достигнуты грандиозные успехи. Сейчас повсеместно имеются вычислительные центры, оснащенные современной электронной вычислительной техникой, способной выполнять десятки и сотни тысяч операций в секунду. А такие отечественные машины, как ЭВМ класса «БЭСМ», выполняют около миллиона операций в секунду.

Вычислительные машины (как малые, так и большие) делятся на два класса: дискретного и непрерывного действия.

К машинам дискретного действия относятся арифмометры, клавишные механические, электромеханические и электронные цифровые машины. В машинах дискретного действия числа изображаются в обычной цифровой форме в десятичной системе счисления.

В машинах непрерывного действия числа представляются при помощи непрерывных геометрических или физических величин — длин отрезков, углов поворотов, силы тока, напряжения в цепи и т. д.

К машинам и устройствам непрерывного действия относятся логарифмическая линейка, планиметр (устройство для измерения площадей плоских фигур), аналоговые электронные вычислительные машины и др.

Логарифмическая линейка

Логарифмическая линейка — это простое вычислительное устройство, которое с успехом используется в инженерных расчетах.

В основе логарифмической линейки лежит идея сложения чисел при помощи двух скользящих линеек с нанесенными на них одинаковыми равномерными шкалами. Например, для нахождения суммы 6+7 при помощи таких двух линеек (рис. 1) сдвигаем начальную

точку одной:из шкал на отрезок, равный первому слагаемому, т. е. отметка 0 на подвижной шкале должна совпадать с отметкой 6 на неподвижной шкале. Отмечая на подвижной шкале значение второго
слагаемого^-числа 7, находим на неподвижной шкале значение суммы 13.

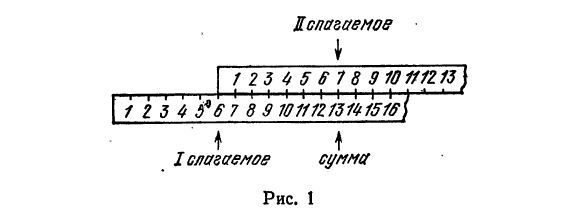
В логарифмической линейке вместо равномерных шкал используются логарифмические шкалы, в которых длина соответствующего отрезка равна логарифму представляемого числа В этом случае сумме отрезков будет соответствовать сумма логарифмов отмеченных чисел. Но, как известно, сумма логарифмов равна логарифму

произведения 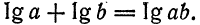Следовательно, при помощи таких скользящих логарифмических шкал можно выполнять умножение и деление чисел (рис. 2).

Устройство и правила применения логарифмической
линейки в вычислениях нам известны из курса средней школы.

Арифмометр

Это одна из самых простых и распространенных механических вычислительных машин. Первый арифмометр был предложен в 1670 г. немецким

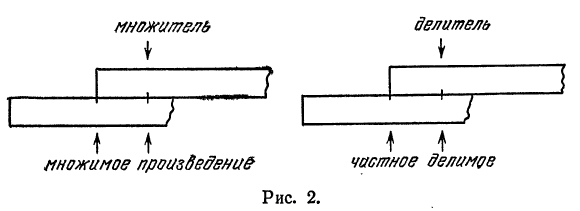
математиком Лейбницем. На арифмометре можно выполнять все четыре арифметических действия. Отечественный арифмометр «Феликс» (рис. 3) состоит из неподвижного корпуса, главной частью которого является барабан с рычажками для установления чисел 2,
и передвижной каретки 5.

С правой стороны барабана находится оперативная рукоятка 4, вращающая вал 1, на котором расположены счетные колеса Однера. Исходные данные устанавливаются посредством перемещения рычажков 2 вдоль прорезей на барабане. В правой части передвижной каретки имеется 13-разрядный счетчик результатов 7, а в ее левой части имеется 8-разрядный счетчик оборотов 8 вращения рукоятки.

Перед началом работы каждый раз арифмометр необходимо привести в исходное положение. Для этого нужно погасить показания всех счетчиков, установить рычажки против нулей и поставить каретку 5 при помощи рычага перемещения каретки 15 в крайнее левое
положение.

Сложение

Пусть требуется вычислить сумму

При помощи рычажков набираем на барабан арифмометра первое слагаемое 3275. Для этого первый рычажок (считая справа) ставим против цифры 5, второй —

против цифры 7, третий — против цифры 2 и четвертый—против цифры 3. Одним полным поворотом рукоятки по ходу часовой стрелки (т.е.в сторону стрелки, отмеченной знаками «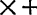», такие повороты будем называть положительными) переносим это число в счетчик результатов.

В окошках счетчика результатов покажется число После этого гасим число 3275 на установочном

барабане и набираем при помощи рычажков в таком же порядке второе слагаемое 1241. Выполняем рукояткой еще один положительный оборот. В окошках счетчика результатов появится число 4516, т. е. сумма чисел 3275 и 1241. Дальше продолжаются те же действия. Гасим на барабане число 1241, набираем следующее
слагаемое 729 и выполняем один положительный оборот рукоятки. В окошках счетчика результатов читаем искомую сумму 5245.

Так можно сложить любое число слагаемых при условии, что сумма не превысит* емкость счетчика результатов, т. е. для 13-разрядного счетчика результатов не превысит числа 9 999 999 999 999.

Вычитание

Для нахождения разности двух чисел установим уменьшаемое в счетчике результатов. Набираем на барабане вычитаемое и выполним один полный оборот рукоятки против часовой стрелки (т.е. в сторону стрелки, отмеченной знаками «— :», такие повороты будем
называть отрицательными). В итоге в окошках счетчика результатов читаем значение искомой разности.

Комбинируя вращения рукоятки в положительную и отрицательную стороны (в зависимости от знака соответствующих чисел), можно вычислять любые алгебраические суммы при условии, что как все
промежуточные, так и окончательный результаты являются положительными.

Замечание:

При выполнении сложения и вычитания можно не обращать внимание на цифры, появляющиеся в окошках счетчика оборотов.

Пример:

Вычислить 2341 — 1292+123 — 425.

Решение:

Устанавливаем на барабане арифмометра при помощи рычажков число 2341 и одним положительным поворотом рукоятки переносим его в счетчик результатов. Потом устанавливаем на барабане число 1292 и выполняем один отрицательный поворот
рукоятки. В счетчике результатов прочтем число 1049. Устанавливаем на барабане число 123 и выполняем один положительный оборот рукоятки. В счетчике результатов появится число 1172. Наконец, устанавливаем на барабане число 425 и выполняем один отрицательный поворот, после чего в счетчике результатов читается окончательный ответ 747.

Умножение

Действие умножения выполняется посредством повторного сложения.

Пример:

Вычислить 4293 437.

Решение:

Устанавливаем на барабане один из сомножителей. Для уменьшения числа оборотов рекомендуется устанавливать на барабане сомножитель, у которого больше сумма цифр. В нашем случае таким является первый сомножитель 4293. После этого рукояткой делаем 7 положительных оборотов. В счетчике результатов появится число 30051, это — произведение 4293 7. В счетчике оборотов появится цифра 7 (белая). Передвигаем каретку на один шаг вправо и выполняем три положительных оборота. В счетчике результатов появится число 158841, а в счетчике оборотов— число 37. Наконец, передвигаем каретку еще на один шаг вправо и выполняем 4 положительных оборота. В счетчике результатов прочтем окончательный результат 1876041, а в счетчике оборотов — значение второго сомножителя 437

7. В счетчике оборотов появится цифра 7 (белая). Передвигаем каретку на один шаг вправо и выполняем три положительных оборота. В счетчике результатов появится число 158841, а в счетчике оборотов— число 37. Наконец, передвигаем каретку еще на один шаг вправо и выполняем 4 положительных оборота. В счетчике результатов прочтем окончательный результат 1876041, а в счетчике оборотов — значение второго сомножителя 437.

Заметим, что разными способами можно уменьшить количество выполняемых поворотов рукоятки. Так, в нашем случае при умножении на 7 вместо того, чтобы выполнить первые 7 положительных оборотов рукоятки, можно передвинуть каретку на один шаг вправо и выполнить одни положительный поворот (что соответствует умножению на 10), передвинуть каретку обратно на один шаг влево и выполнить три отрицательных оборота рукоятки. В счетчике результатов будет число 30051 (умножение на 7). При таком способе умножения в счетчике оборотов не окажется второй сомножитель, там появятся и красные цифры.

Деление

Пусть требуется разделить 74678 на 534. Устанавливаем рычажками на барабане делимое 74678 и переносим его в счетчик результатов. После этого гасим число на барабане и единицу в счетчике оборотов.
Устанавливаем делитель 534 на барабане. Теперь передвигаем каретку вправо до тех пор, пока первая слева цифра делителя (т, ef первый рычаг слева, передвинутый с нулевой позиции) не будет над первой слева цифрой делимого (который записан в счетчике результатов)

После этого выполняем столько отрицательных поворотов рукоятки, пока не раздастся звонок и в счетчике вместо крайних левых нулей не появятся девятки. Если первая цифра делителя больше первой цифры делимого, то такое положение наступит после первого же поворота. При помощи одного или, быть может, двух, трех (но не лишних) положительных оборотов восстанавливаем нули в крайних левых окошках счетчика результатов. В нашем случае звонок и девятки появятся на втором отрицательном повороте рукоятки, после чего выполняем один корректирующий положительный поворот. В счетчике результатов восстановится остаток 21278. Переводим на один разряд каретку влево и опять вращаем рукоятку в отрицательном направлении до появления звонка. В нашем случае это будет на четвертом обороте. Положительным оборотом восстанавливаем остаток 5258. Передвигаем каретку на один разряд влево и вращаем рукоятку в отрицательном направлении до звонка. Теперь звонок раздастся на 10-м повороте. Положительным поворотом восстанавливаем остаток 452.

В счетчике оборотов читаем значение частного 139 (при этом цифры 1 и 3 красные, а цифра 9 белая), в счетчике результатов читаем значение остатка 452, т. е. 74678 = 534 139 + 452.

Действия над десятичными дробями

Для выполнения сложения и вычитания и вообще алгебраического сложения точных чисел, представленных десятичными дробями, используются передвижные запятые на каретке и барабане.

Пример:

Найти значение выражения

121,702 — 24,3 + 732,04 — 501,0042.

Решение:

Определим, каково наибольшее число десятичных знаков в заданных числах. В нашем случае это число равно 4. Приписывая соответствующее число нулей, т. е. приводя дроби к общему знаменателю, представим каждое число с четырьмя десятичными знаками: 121,7020 — 24,3000 + 732,0400 — 501,0042. После этого запятую на счетчике результатов устанавливаем между четвертым и пятым окошками. Сейчас действия над данными числами выполняются так же, как и над целыми числами.

В итоге со счетчика результатов снимаем ответ с учетом запятой: 328,4378.

При умножении десятичных дробей отвлекаемся от наличия запятой, умножаем соответствующие целые числа и в полученном произведении отделяем справа столько десятичных знаков, сколько имеется их вместе в обоих сомножителях.

Пример:

Найти произведение 374,05 25,175.

Решение:

Имеем: 37405 25175 = 941670875. В первом сомножителе имеются 2 десятичных знака, во втором — 3 и 2 + 3 = 5, следовательно,

374,05 25,175 = 9416,70875.

Деление десятичных дробей можно выполнить различными4 способами. Укажем один из них: деление с наперед заданной точностью. Пусть требуется разделить 382,05 на 63,571 с точностью до 0,0001. Установим запятую на счетчике оборотов между четвертым и пятым справа окошками, отделяя таким образом четыре десятичных разряда. Приведем данные числа к общему знаменателю. В нашем примере делимое нужно взять в виде 382,050. Отмечаем запятой над барабаном три разряда и набираем на барабане делимое 382,050.
Передвигаем каретку вправо на четыре шага (в соответствии с требуемыми четырьмя десятичными знаками в частном) и переносим делимое одним положительным оборотом рукоятки в счетчик результатов. Установим запятую на счетчике результатов против запятой на барабане, в нашем случае между седьмым и восьмым окошками.

Имеется ряд усовершенствованных моделей арифмометров. К ним, например, относятся машины типа ВК (ВК-1, ВК-2, ВК-3). В арифмометрах этого типа набор чисел клавишный, передвижная каретка заменена более совершенными устройствами, заключенными в корпусе машины.

В некоторых моделях оперативная рукоятка отсутствует, машина снабжена электроприводом. Имеются также различные типы электромеханических машин, например, полноклавишная вычислительная машина-автомат ВММ-2. Многие операции в этих
машинах выполняются в полуавтоматическом режиме.

В последнее время все большее распространение получают настольные и портативные электронные вычислительные машины на полупроводниках и интегральных схемах.

Настольные электронные клавишные вычислительные машины «Искра», «Электроника»

Вычислительная машина «Искра» разработана в Институте кибернетики АН УССР в 1966 г. и предназначена для выполнения научно-технических и учетно-статистических расчетов. Ввод чисел производится путем нажатия соответствующих клавиш. Набранные числа и результаты действий наблюдаются на индикаторных лампах.
На машинах «Искра» можно выполнять, с учетом знаков и запятых, над 16-разрядными десятичными числами такие операции, как сложение, вычитание, умножение, деление, нахождение процентов, извлечение квадратного корня, вычисление значений тригонометрических, показательных, логарифмических функций, накопление — алгебраическое суммирование результата произведенного действия с содержимым накапливающего регистра. Операции производятся в автоматическом и полуавтоматическом режимах.

Широкое распространение получили настольные и портативные электронные клавишные вычислительные машины отечественного производства типа «Электроника». Машины типа «Электроника» имеют весьма небольшие размеры и вес, работают от электросети или от химических элементов.

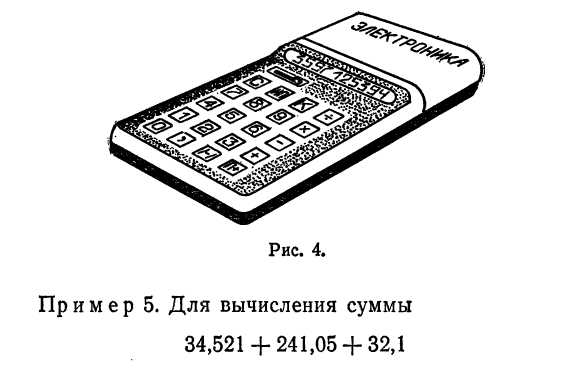
На машине «Электроника БЗ-24» выпуск 1977 г. (рис. 4) и других родственных моделях можно выполнять все четыре арифметических действия над положительными и отрицательными числами. Кроме того, имеется устройство памяти, при помощи которого можно вычислять алгебраические суммы. Имеется также устройство работы с константой для умножения и деления ряда чисел на одно и то же число. На этой машине среднее время выполнения одной арифметической операции 0,5 сек.

Набор данных й команды для выполнения операций производятся нажатием соответствующих клавиш. Окончательный результат выводится на световом индикаторе нажатием клавиши .

достаточно нажать поочередно клавиши соответствующего наименования:

Для получения результата необходимо, как и в любом случае, нажать клавишу . На световом индикаторе читаем результат 307,671.

Для вычисления произведения или частного также нажимаются поочередно клавиши соответствующего наименования. Для прочтения результата нажимается, как всегда, клавиша .

Пример:

Для вычисления произведения 2,301 47,5 нажимаются клавиши

и на световом индикаторе читается результат 109,2975.

Пример:

Для вычисления частного 2,301 : 47,5 таким же образом нажимаем соответствующие клавиши.

В нашем случае на шестом месте нужно нажать клавишу . В конце, после нажатия клавиши на индикаторе читаем результат 0,0484421.

Пример:

Для вычисления алгебраической суммы

34,521 — 241,05 + 32,1 = 34,521 + (—241,05)+ 32,1

после набора числа 34,521 нажимается клавиша , после этого набирается число 241,05 и изменяется его знак нажатием клавиши , т. е. для вычисления этого выражения нужно нажимать клавиши в следующем рядке;

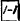
На индикаторе читается ответ: — 174,429.

При более сложных вычислениях для выполнения промежуточных алгебраических сумм, произведений или частных используется память.

Пример:

Вычислить: (3,4 2 — 0,5 1,5 4:0,2) З.

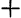
Решение:

Нажимаем клавиши в следующем порядке:

На индикаторе читаем ответ 78,15.

Имеются модели машин типа «Электроника» также портативного формата, которые выполняют до 32-х операций, среди них — нахождение значений тригонометрических и других функций.

Электронные вычислительные машины

Вычислительные центры нашей страны снабжены различными электронными вычислительными машинами, как цифровыми дискретного действия (ЭЦВМ), так и аналоговыми (ABM). ABM являются, как правило, специализированными машинами. Специализированные ЭВМ
строятся для определенной цели. Так, имеются управляющие машины, машины для решения некоторого узкого класса задач, например, для предсказания погоды, для решения специальных экономических задач, обработки информации и т. д. Универсальные ЭВМ предназначены для решения широкого круга задач. Любая современная универсальная ЭЦВМ включает в себя следующие основные узлы:

Устройство ввода данных служит для ввода числовых данных и программ в машину. УВ может быть построено на различных принципах. Клавиатурные
устройства являются простыми и эффективными
устройствами непосредственного ввода данных в машину, но
имеют ограниченную скорость ввода данных. Устройства
считывания требуют предварительной подготовки
данных, их фиксирования на тех или иных носителях
информации (перфокартах, перфолентах, магнитных лентах,
дисках, барабанах, электронно-лучевых трубках и др.).
Такие устройства обеспечивают высокую скорость ввода
данных и допускают многократное использование.
Эффективными могут оказаться в будущем устройства
распознавания речевых сигналов, в которых информация
будет подаваться в форме речевых команд.

Устройство вывода предназначено для выдачи результатов вычислений на различные носители информации. Самыми распространенными и довольно удобными являются алфавитно-цифровые печатающие устройства (АЦПУ), которые представляют данные в виде обычного печатного текста. В некоторых случаях,
результаты выдаются на перфолентах, на световых табло. Для ввода и вывода тех или иных особых форм информации, например, графической, создаются специальные устройства ввода — вывода.

Арифметическое устройство — это, собственно, вычислительная часть машины. АУ предназначено для выполнения арифметических операций, операций сравнения чисел, различных преобразований чисел (изменения; знака, сдвига), а также логических операций. На такие операции распадается любой вычислительный процесс. Основой АУ является сумматор, который выполняет сложение чисел. Остальные операции сводятся к однократному или многократному сложению и некоторым другим вспомогательным операциям, например, сдвигам при умножении.

Запоминающее устройство выполняет функции приема, хранения и выдачи всей требуемой информации (исходных данных, промежуточных результатов, программ вычислений, окончательных результатов вычислений).

Устройство управления обеспечивает координацию действий всех устройств ЭВМ, автоматически управляя всем вычислительным процессом в соответствии с программой решения задачи.

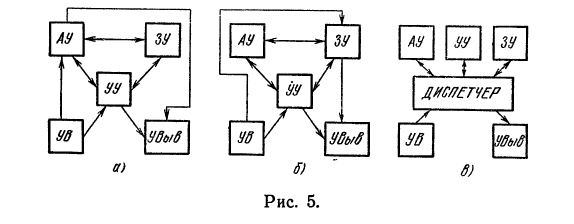
Логические связи между отдельными устройствами ЭВМ, определяющие движение информации, могут быть реализованы по различным схемам. На рис. 5, а указаны логические связи в первых образцах ЭЦВМ, в которых информация при вводе и выводе проходила через

АУ. На рис. 5,6 представлена схема проектирования последующих систем ЭЦВМ, в которых информация проходит через ЗУ. В таких машинах удается совместить по времени работу устройств ввода — вывода с вычислительным процессом в АУ, что повышает производительность машины. Логические связи устройств в
современных машинах, например, в машине БЭСМ-6,
координирует так называемый «диспетчер», который организует одновременную работу различных устройств ЭВМ (рис. 5,в). Диспетчер состоит из программы — диспетчера, который управляет прохождением заданий в ЭЦВМ, и специального устройства, обеспечивающего необходимые связи устройств ЭЦВМ.

Основными параметрами, характеризующими качество различных типов ЭВМ, являются быстродействие, объем памяти, состав устройств ввода — вывода, надежность, полезное время и др.

Быстродействие — это характеристика скорости работы машины, которая измеряется средним количеством машинных операций, выполняемых за единицу времени. Быстродействие малой машины «Проминь» — около 100 операций в секунду, а большой машины БЭСМ-6— около 1 млн. операций в секунду. Быстродействие ЭВМ
зависит от быстродействия АУ, ЗУ и других ее узлов.

В настоящее время как теория, так и практика проектирования вычислительных систем развиваются быстрыми темпами, создаются новые, более совершенные типы машин, необходимых для решения научных и народнохозяйственных задач.

Приближенные числа

Из курса математики средней школы нам известны характеристики приближенных чисел и действия над ними. Несмотря на это, учитывая важность приближенных вычислений как для усвоения специальных и технических дисциплин, так и для практической работы, мы повторим еще раз основные вопросы теории
приближенных вычислений.

Источники приближенных чисел

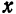
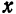
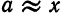
Число называется приближенным значением или приближением некоторой величины (или просто приближенным числом), если — число, близкое к истинному значению а данной величины. В таких случаях пишут . Например,

Основными источниками приближенных чисел являются; измерение непрерывных величин (расстояния» времени, веса, температуры, силы тока и т. д.), определение количества элементов больших множеств, выполнение арифметических операций, вычисление значений функций.

Абсолютная и относительная погрешности

Основными характеристиками приближенных чисел
являются абсолютная и относительная погрешности. Пусть
— приближение величины .

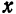
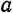
Определение:

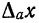
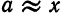
Абсолютной погрешностью приближения называется модуль разности , т. е.

Отсюда следует, что или
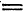
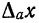
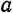
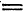
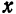
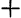
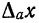
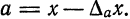
т. е. или В таких случаях пишут:

Пример:

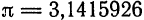
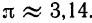
Известно, что … Найдем абсолютную погрешность приближения Имеем

Этот пример показывает, что точное значение абсолютной погрешности, как и точное значение рассматриваемой величины, является, вообще говоря, громоздким числом, неудобным для вычислений. Больше того, часто точное значение рассматриваемой величины является неизвестным, следовательно, неизвестным
является и точное значение абсолютной погрешности. Поэтому для характеризации точности приближения вводится понятие границы абсолютной погрешности.

Определение:

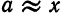
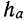
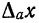
Границей абсолютной погрешности приближения называется такое положительное число которое больше (или равно) абсолютной погрешности :

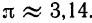
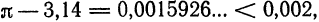
П р и м е р 2. Для приближения так как
можно взять

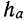
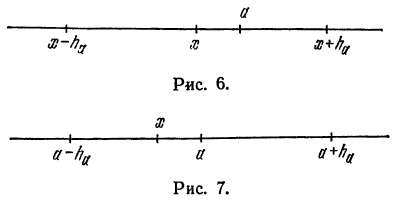
В отличие от абсолютной погрешности граница абсолютной погрешности не определяется однозначно. Поэтому на практике в качестве границы абсолютной погрешности берется по возможности наименьшее число, которое удобно для вычислений и обеспечивает необходимую точность.

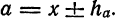
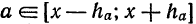
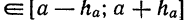
Условимся писать Эта запись означает, что (рис. 6) и, аналогично,
(рис. 7). Легко видеть, что

Пример:

Для некоторой машины нужна круглая деталь диаметром 24 мм. Известно из практики, что машина работает нормально, если диаметр детали отличается от заданного не более, чем на ±0,5 мм, т. е d = 24 ± 0,5 мм, или 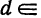[24 — 0,5; 24 + 0,5].

Абсолютная погрешность, так же как и граница абсолютной погрешности, не достаточна для полной характеристики приближения. Пусть, например, при измерении длины радиоволны абсолютная погрешность равна одному метру. Для длинных радиоволн порядка 1000 м это будет хорошая точность, в то время как для коротких волн, длина которых около 40 м, ошибка измерений окажется слишком большой. Таким образом, для более полной характеристики точности измерения необходимо определить, какую часть, или сколько процентов, составляет абсолютная погрешность от
значения данной величины.

Определение:

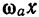
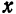
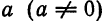
Относительной погрешностью приближенного числа называется отношение абсолютной погрешности этого числа к модулю точного значения данной величины, т. е.

Определение:

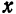
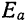
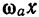
Границей относительной погрешности приближения точного числа а называется положительное число которое больше (или равно) относительной погрешности , т. е.

Если задана граница абсолютной погрешности 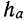, то

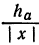
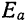
Как правило, число берется в качестве границы относительной погрешности :

Пример:

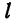
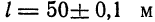
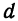
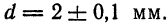
При измерениях для длины некоторого провода получено значение , для диаметра — значение Вычислим границы относительных погрешностей

В процентах имеем 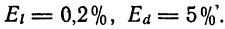Эти данные показывают, что измерение длины проведено более точно, чем измерение диаметра провода. Из (3) получаем формулу

для определения границы абсолютной погрешности, если известна граница относительной погрешности.

Пример:

Для приближения 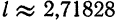граница
относительной погрешности равна 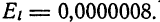Найти
границу абсолютной погрешности

Решение:

По формуле (2) имеем

Запись приближенных чисел. Верные и значащие цифры

Определение:

Цифра 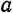в представлении приближенного числа десятичной дробью называется верной, если абсолютная погрешность числа не превосходит единицы того разряда, в котором записана эта
цифра. В противном случае она называется сомнительной.

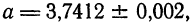
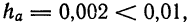
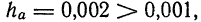
Например, если то цифра 4 верная, так как следовательно, предыдущие цифры 7 и 3 также верны; цифра 1 сомнительная, так как тем более следующая цифра 2 является сомнительной.

Для записи приближенных Чисел десятичными дробями принимается следующее правило: если не указывается граница абсолютной погрешности, то приближение записывается так, чтобы все записанные цифры были верные. Так, в случае последнего примера следует писать

Отсюда следует, что, в отличие от случая точных чисел, когда, например, 0,03 = 0,030 = 0,0300, записи 0,03, 0,030, 0,300 как изображения приближенных чисел неравносильны. В самом деле, запись 0,03 показывает, что абсолютная погрешность меньше 0,01, записи 0,030 и 0,0300 показывает, что здесь имеем более высокую
точность, соответственно 0,001 и 0,0001.

Если цифра- нуль сомнительна, то это указывается особо. В записях это делается словесным выражением. Например, мы говорим: «Население СССР на 15.1.1970 г, составляло 241720 тысяч человек». Такая запись показывает, что цифры сотен, десятков и единиц являются сомнительными. Следовательно, это число нельзя представить в виде 241720 000. В науке (особенно, в физике, технике) вместо словесного выражения пишется множитель вида 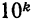. Так, рассмотренное выше приближенное число пишется в виде

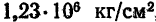
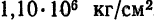
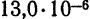
Рассмотрим еще некоторые примеры. В справочниках читаем: модуль упругости тянутой меди равен , литой меди , коэффициент линейного расширения никеля равен .

Определение:

Все верные цифры, кроме нулей, расположенных левее первой отличной от нуля цифры, называются значащими цифрами.

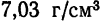
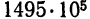
Например, в числе (плотность серого чугуна) имеются три значащие цифры, в числе км (расстояние от Земли до Солнца) — четыре значащие цифры в числе 4400 км (длина реки Лена) — четыре значащие цифры, в числе 0,000270 (коэффициент линейного расширения олова)—три значащие цифры.

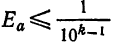
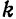
Если по разряду последней верной цифры можно определить границу абсолютной погрешности приближенного числа, то по количеству значащих цифр можно оценить границу относительной погрешности. Так, из формулы (3) легко получить, что , если приближенное число имеет значащих цифр.

Пример:

В числе последняя верная цифра — это цифра сотен, следовательно, , число значащих цифр . Тогда

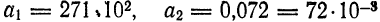
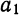
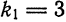
Аналогично, 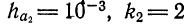и

Порядок малости величин. Приближенные формулы

Две величины называются величинами одного порядка, если с точки зрения допустимой абсолютной погрешности разность между ними незначительна. Для величин, меньших единицы, в качестве количественной характеристики порядка малости обычно берется
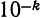
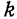
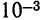
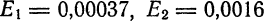
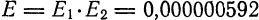
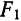
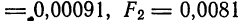
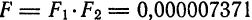
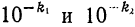
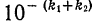
число , где — число нулей между запятой и первой отличной от нуля цифрой. Например, числа 0,00034 и 0,00041 имеют один и тот же порядок малости . Легко видеть, что произведение двух малых величин имеет более высокий порядок малости, чем данные сомножители. Например, пусть . Тогда . Для чисел имеем . Легко видеть, что если сомножители имеют порядок малости , то их произведение имеет порядок малости не ниже .

Если данные величины имеют одинаковый порядок малости, то их произведение имеет, по крайней мере, вдвое более высокий порядок малости. В связи с этим на практике пользуются следующим правилом: если 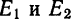имеют близкие порядки малости, то можно пренебрегать слагаемыми, равными их произведению или их степеням. При помощи этого правила приводятся приближенные
формулы. Рассмотрим некоторые примеры таких формул Пусть — малое число. Тогда

Источник