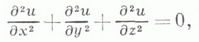Что изучает математическая физика
Математическая физика
Вы будете перенаправлены на Автор24
Около трехсот лет назад стали возникать теории построение математических моделей, которые напрямую или косвенно были связаны с исследованиями в области физики. Впервые такую взаимосвязь внес в своих научных трудах британский ученый-теоретик Исаак Ньютон. В годы своей жизни он пытался разобраться с понятием всемирного тяготения, в теории существования и распространение света, а также изучал основы классической механики. Тогда он придумал совместить два направления в науки в единое целое, что позже стало называться математической физикой.
Через некоторое время труды английского исследователя подхватили иные представители научного мира. Свои математические модели представили остальные европейские ученые. В развитие информационных технологий внесли свой ощутимый вклад и российские ученые, работавшие над теоретическими размышлениями в конце 19 века.
Сегодня мы понимаем математическую физику как обобщенное название методов математического исследования. Такие модели описывают в форме сложных уравнений, в том числе интегральных и дифференциальных.
Применение математической физики
При проведении теоретических исследований в сфере квантовой физики и научного подтверждения теории относительности, сформулированной около века назад Альбертом Эйнштейном, в настоящее время нашло воплощение в компьютерных вычислениях различных областях математической физики. Это сформировало новые разделы предмета теоретических исследований и многократно увеличило шансы на поиск конечного результата и применения найденных результатов на практике. С помощью вычислительных машин в настоящее время проводятся точные вычисления в теории обобщенных функций, комплексных переменных, применяются алгебраические и топологические методы. Математические модели участвуют в построении основных закономерностей изучаемого класса физических явлений. Уравнения помогают понять физические процессы, происходящие в любой точке Вселенной, и применить знания на практике.
Готовые работы на аналогичную тему
При построении математических моделей исследователи исходят только от общих основополагающих понятий, которые уже известны и сформулированы в идее понятий и формул, а затем высчитываются второстепенные характеристики явления. Ученые обычно пытаются построить при помощи компьютерных вычислений законы сохранения количества энергии, движение и число частиц. Для описания различных процессов физической природы используются такие же математические модели с общими характерными чертами.
Характерными чертами для математической физики являются общие методы. Их можно использовать для решения различных задач математической физики. Они развивались из частных методов, но до определенного отрезка времени не имели четко сформулированных границ, обращенных в понятия и формулы. Теперь такой процесс пошел ускоренными темпами, что влияет на решение задач, которые долгое время стояли перед математиками и теоретиками. На каком-то этапе все теоретические знания не имели подтверждения в виде точных вычислений и носили общий и приблизительный характер. Сегодня получена возможность обобщить все предыдущие знания и сделать рывок в изучении происходящих физических процессов рывок вперед.
В настоящее время в числе известных методов решения задач математической физики выделяют:
Все эти методы уже в ближайшем будущем получат эффективное применение, что позволит решить конкретные задачи и стать стимулом для дальнейших изучений строгого математического обобщения и обоснования теоретических знаний. В некоторых случаях появится возможность возникновения новых направлений в математике.
Влияние математической физики на различные разделы математики
Математическая физика сильно влияет на иные разделы математики и физики. Это ощущается в отражении требований естественных наук запросов практики. Сложившиеся разделы математики требуют изменений и переориентации в области многих исследований, поэтому в задачи математической физики входит разработка новых математических моделей, направленных на всестороннее изучение физических явлений и установления величин и моделей. Все поставленные задачи решаются при наличии производных и интегральных уравнений, а также вариационными методами.
Математические модели позволяют создать такие методы изучения физики, которые существенно улучшают получение количественных характеристик физических явлений. Исследователи получают возможность рассчитать с большой степенью точности ход реальных процессов, проникать достигать понимания на глубоком уровне суть физических явлений и процессов, выявляются новые закономерности развития и существования явлений, а также предсказываются новые эффекты.
Есть у такой модели познания явлений и ряд негативных признаков. Как и всякая любая модель на математическом уровне не может даже после вычислений дать с точностью понять о физических свойствах явления, поэтому теоретические знания стоит подкреплять практическими исследованиями. Только после них можно говорить об адекватности математической модели и ее степени применения в будущем. Считается, что адекватность принятой модели проверяется только после обоснования решения обратных задач математической физики:
Как пример такого способа построение математической модели служат теоретические опыта Исаака Ньютона и его обоснование увиденного. Теория всемирного тяготения не имела до определенного времени практических доказательств, поскольку наука и техника несколько столетий назад еще не могла экспериментально доказать взаимодействие частиц во всей Солнечной системе. Однако британский ученый смог предсказать заранее, что согласно такому физическому явлению происходит невидимое взаимодействие частиц и это осуществляется не только в земных условиях, но и на других планетах нашей звездной системы.
МАТЕМАТИЧЕСКАЯ ФИЗИКА
— теория математических моделей физических явлений; занимает особое положение и в математике, и в физике, находясь на стыке этих наук.
М. ф. тесно связана с физикой в той части, к-рая касается построения математич. модели, и в то же время М. ф.- раздел математики, поскольку методы исследования моделей являются математическими. В понятие методов М. ф. включаются то математич. методы, к-рые применяются для построения и изучения математич. моделей, описывающих большие классы физических явлений.
Начиная со 2-й пол. 19 в. методы М. ф. успешно применялись для изучения математич. моделей физич. явлений, связанных с различными физич. полями и волновыми процессами в электродинамике, акустике, теории упругости, гидро- и аэродинамике и ряде других направлений исследования физич. явлений в сплошных средах. Математич. модели этого класса явлений наиболее часто описываются при помощи дифференциальных уравнений с частными производными, получивших название математической физики уравнений.
Помимо дифференциальных уравнений М. ф., при описании математич. моделей физики применение находят интегральные уравнения и интегро-дифференциальные уравнения, вариационные и теоретико-вероятностные методы, теория потенциала, методы теории функций комплексного переменного и ряд других разделов математики. В связи с бурным развитием вычислительной математики особое значение для исследования математич. моделей физики приобретают прямые численные методы, использующие ЭВМ (конечноразностные методы и др. вычислительные алгоритмы краевых задач), что позволило методами М. ф. эффективно решать новые задачи газовой динамики, теории переноса, физики плазмы, в том числе и обратные задачи этих важнейших направлений физич. исследований.
Теоретич. исследования в области квантовой физики и теории относительности, широкое использование ЭВМ в различных областях М. ф., включая и обратные (некорректно поставленные) задачи, потребовали значительного расширения используемого М. ф. арсенала математич. методов. Наряду с традиционными разделами математики стали широко применяться теория операторов, теория обобщенных функций, теория функций многих комплексных переменных, тоиологич. и алгебраич. методы. Это интенсивное взаимодействие теоретич. физики, математики и использования ЭВМ в научных исследованиях привело к значительному расширению тематики, созданию новых классов моделей и подняло на новый уровень современную М. ф. Все это внесло большой вклад в развитие научно-технич. прогресса.
Постановка задач М. ф. заключается в построении математич. моделей, описывающих основные закономерности изучаемого класса физич. явлений. Такая постановка состоит в выводе уравнений (дифференциальных, интегральных, интегро-дифференциальных или алгебраических), к-рым удовлетворяют величины, характеризующие физич. процесс. При этом исходят из основных физич. законов, учитывающих только наиболее существенные черты явления, отвлекаясь от ряда его второстепенных характеристик. Такими законами являются обычно законы сохранения, напр., количества движения, энергии, числа частиц и т. д. Это приводит к тому, что для описания процессов различной физич. природы, но имеющих общие характерные черты, оказываются применимыми одни и те же математич. модели. Напр., математич. задачи для простейшего уравнения гиперболич. типа
полученного первоначально Ж. Д’Аламбером (J.D’Alembert, 1747) для описания свободных колебаний однородной струны, оказываются применимыми и для описания широкого круга волновых процессов акустики, гидродинамики, электродинамики и других областей физики. Аналогично, уравнение
краевые задачи для к-рого первоначально изучались П. Лапласом (P. Laplace, кон. 18 в.) в связи с построением теории тяготения, в дальнейшем нашло применение при решении многих проблем электростатики, теории упругости, задач установившегося движения идеальной жидкости и т. д. Каждой математич. модели физики соответствует целый класс физич. процессов. Для М. ф. характерно также то, что многие общие методы, используемые для решения задач М. ф., развились из частных способов решения конкретных физич. задач и в своем первоначальном виде не имели строгого математич. обоснования и достаточной завершенности. Это относится к таким известным методам решения задач М. ф., как методы Ритца и Галеркина, к методам: теории возмущений, преобразований Фурье и многим другим, включая метод разделения переменных. Эффективное применение всех этих методов для решения конкретных задач является одной из причин для их строгого математич. обоснования и обобщения, приводящего в ряде случаев к возникновению новых математич. направлений.
Воздействие М. ф. на различные разделы математики проявляется в том, что развитие М. ф., отражающее требования естественных наук и запросы практики, влечет за собой переориентацию направленности исследований в нек-рых уже сложившихся разделах математики. Постановка задач М. ф., связанная с разработкой математич. моделей реальных физич. явлений, привела к изменению основной проблематики теории дифференциальных уравнений с частными производными. Возникла теория краевых задач, позволившая впоследствии связать дифференциальные уравнения с частными производными с интегральными уравнениями и вариационными методами.
Изучение математич. моделей физики математич. методами не только позволяет получить количественные характеристики физич. явлений и рассчитать с заданной степенью точности ход реальных процессов, но и дает возможность глубокого проникновения в самую суть физич. явлений, выявления скрытых закономерностей, предсказания новых эффектов. Стремление к более детальному изучению физич. явлений приводит к все большему усложнению описывающих эти явления математич. моделей, что в свою очередь делает невозможным применение аналитич. методов исследования этих моделей. Это объясняется, в частности, тем, что математич. модели реальных физич. процессов являются, как правило, нелинейными, т. е. описываются нелинейными уравнениями М. ф. Для детального исследования таких моделей успешно применяются прямые численные методы с использованием ЭВМ. Для типичных задач М. ф. применение численных методов сводится к замене уравнений М. ф. для функций непрерывного аргумента алгебраич. уравнениями для сеточных функций, заданных на дискретном множестве точек (на сетке). Иными словами, вместо непрерывной модели среды вводится ее дискретный аналог. Применение численных методов в ряде случаев позволяет заменить сложный, трудоемкий и дорогостоящий физич. эксперимент значительно более экономичным математическим (численным) экспериментом. Достаточно полно проведенный математич. эксперимент является основой для выбора оптимальных условий реального физич. эксперимента, выбора параметров сложных физич. установок, определения условий проявления новых физич. эффектов и т. д. Таким образом, численные методы необычайно расширяют область эффективного использования математич. моделей физич. явлений.
Математич. модель физич. явления, как всякая модель, не может передать всех черт явления. Установить адекватность принятой модели исследуемому явлению можно только при помощи критерия практики, сопоставляя результаты теоретич. исследований принятой модели с данными экспериментов.
Во многих случаях об адекватности принятой модели можно судить на основании решения обратных задач М. ф., когда о свойствах изучаемых явлений природы, недоступных для непосредственного наблюдения, делаются заключения по результатам их косвенных физич. проявлении.
Для М. ф. характерно стремление строить такие математич. модели, к-рые не только дают описание и объяснение уже установленных физич. закономерностей изучаемого круга явлений, но и позволяют предсказать еще не открытые закономерности. Классич. примером такой модели является теория всемирного тяготения Ньютона, позволившая не только объяснить движение известных к моменту ее создания тел Солнечной системы, но и предсказать существование новых планет. С другой стороны, появляющиеся новые экспериментальные данные не всегда могут быть объяснены в рамках принятой модели. Для их объяснения требуется усложнение модели.
Лит.:[1] Т и х о н о в А. Н., Самарский А. А., Уравнения математической физики, 4 изд., М., 1972; [2] В л а д и м и р о в В. С., Уравнения математической физики, 4 изд., М., 1981; [3] Соболев С. Л., Уравнения математической физики, 4 изд., М., 1966; [4] К у р а н т Р., Уравнения с частными производными, пер. с англ., М., 1964; [5] М о р с Ф. М., Ф е ш б а х Г., Методы теоретической физики, пер. с англ., т. 1, М., 1958. А. Н. Тихонов, А. А. Самарский, А. Г. Свешников.
Почему математика хорошо описывает реальность?

Поводом к переводу статьи стало то, что я искал книгу автора «The Outer Limits of Reason». Спиратить книгу я так и не смог, зато наткнулся на статью, которая в довольно сжатом виде показывает взгляд автора на проблему.
Вступление
Одна из самых интересных проблем философии науки — это связь математики и физической реальности. Почему математика так хорошо описывает происходящее во вселенной? Ведь многие области математики были сформированы без какого-либо участия физики, однако, как в итоге оказалось, они стали основой в описании некоторых физических законов. Как это можно объяснить?
Наиболее явно этот парадокс можно наблюдать в ситуациях, когда какие-то физические объекты были сначала открыты математически, а уже потом были найдены доказательства их физического существования. Наиболее известный пример — открытие Нептуна. Урбен Леверье сделал это открытие просто вычисляя орбиту Урана и исследуя расхождения предсказаний с реальной картиной. Другие примеры — предсказание Дираком о существовании позитронов и предположение Максвелла о том, что колебания в электрическом или магнитном поле должно порождать волны.
Ещё более удивительно, что некоторые области математики существовали задолго до того, как физики поняли, что они подходят для объяснения некоторых аспектов вселенной. Конические сечения, изучаемые ещё Аполлонием в древней Греции, были использованы Кеплером в начале 17 века для описания орбит планет. Комплексные числа были предложены за несколько веков до того, как физики стали использовать их для описания квантовой механики. Неевклидова геометрия было создана за десятилетия до теории относительности.
Почему математика так хорошо описывает природные явления? Почему из всех способов выражения мыслей, математика работает лучше всего? Почему, например, нельзя предсказать точную траекторию движения небесных тел на языке поэзии? Почему мы не можем выразить всю сложность периодической таблицы Менделеева музыкальным произведением? Почему медитация не сильно помогает в предсказании результата экспериментов квантовой механики?
Лауреат нобелевской премии Юджин Вигнер, в своей статье «The unreasonable effectiveness of mathematics in the natural sciences», также задается этими вопросами. Вигнер не дал нам каких-то определенных ответов, он писал, что «невероятная эффективность математики в естественных науках — это что-то мистическое и этому нет рационального объяснения».
Альберт Эйнштейн по этому поводу писал:
Как может математика, порождение человеческого разума, независимое от индивидуального опыта, быть таким подходящим способом описывать объекты в реальности? Может ли тогда человеческий разум силой мысли, не прибегая к опыту, постичь свойства вселенной? [Einstein]
Давайте внесем ясность. Проблема действительно встает, когда мы воспринимаем математику и физику как 2 разные, превосходно сформированные и объективные области. Если смотреть на ситуацию с этой стороны, то действительно непонятно почему эти две дисциплины так хорошо работают вместе. Почему открытые законы физики так хорошо описываются (уже открытой) математикой?
Этот вопрос обдумывался многими людьми, и они дали множество решений этой проблемы. Теологи, например, предложили Существо, которое строит законы природы, и при этом использует язык математики. Однако введение такого Существа только все усложняет. Платонисты (и их кузены натуралисты) верят в существование «мира идей», который содержит все математические объекты, формы, а так же Истину. Там же находятся и физические законы. Проблема с Платонистами в том, что они вводят ещё одну концепцию Платонического мира, и теперь мы должны объяснить отношение между тремя мирами (прим. переводчика. Я так и не понял зачем третий мир, но оставил как есть). Так же встает вопрос являются ли неидеальные теоремы идеальными формами (объектами мира идей). Как насчет опровергнутых физических законов?
Наиболее популярная версия решения поставленной проблемы эффективности математики заключается в том, что мы изучаем математику, наблюдая за физическим миром. Мы поняли некоторые свойства сложения и умножения считая овец и камни. Мы изучили геометрию, наблюдая за физическими формами. С этой точки зрения, неудивительно, что физика идет за математикой, ведь математика формируется при тщательном изучении физического мира. Главная проблема с этим решением заключается в том, что математика неплохо используется в областях, далеких от человеческого восприятия. Почему же спрятанный мир субатомных частиц так хорошо описывается математикой, изученной благодаря подсчетам овец и камней? почему специальная теория относительности, которая работает с объектами, двигающимися со скоростями близкими к скорости света, хорошо описывается математикой, которая сформирована наблюдением за объектами, двигающимися с нормальной скоростью?
В двух статьях (раз, два) Макр Зельцер и Я (Носон Яновски) сформулировали новый взгляд на природу математики (прим. переводчика. В целом в тех статьях написано то же, что и здесь, но куда более развернуто). Мы показали, что также, как и в физике, в математике огромную роль играет симметрия. Такой взгляд дает довольно оригинальное решение поставленной проблемы.
Что есть физика
Прежде чем рассматривать причину эффективности математики в физике, мы должны поговорить о том, что такое физические законы. Говорить, что физические законы описывают физические феномены, несколько несерьезно. Для начала можно сказать, что каждый закон описывает много явлений. Например закон гравитации говорит нам что будет, если я уроню свою ложку, также он описывает падение моей ложки завтра, или что будет если я уроню ложку через месяц на Сатурне. Законы описывают целый комплекс разных явлений. Можно зайти и с другой стороны. Одно физическое явление может наблюдаться совершенно по-разному. Кто-то скажет, что объект неподвижен, кто-то, что объект движется с постоянной скоростью. Физический закон должен описывать оба случая одинаково. Также, например, теория тяготения должна описывать мое наблюдение падающей ложки в двигающимся автомобиле, с моей точки зрения, с точки зрения моего друга, стоящего на дороге, с точки зрения парня, стоящего у него на голове, рядом с черной дырой и т.п.
Встает следующий вопрос: как классифицировать физические явления? Какие стоит группировать вместе и приписывать одному закону? Физики используют для этого понятие симметрии. В разговорной речи слово симметрия используют для физических объектов. Мы говорим, что комната симметрична, если левая её часть похожа на правую. Иными словами, если мы поменяем местами стороны, то комната будет выглядеть точно также. Физики немного расширили это определение и применяют его к физическим законам. Физический закон симметричен по отношению к преобразованию, если закон описывает преобразованный феномен таким же образом. Например, физические законы симметричны по пространству. То есть явление, наблюдаемое в Пизе, так же может наблюдаться в Принстоне. Физические законы также симметричны по времени, т.е. эксперимент, проведенный сегодня должен дать такие же результаты, как если бы его провели завтра. Ещё одна очевидная симметрия — ориентация в пространстве.
Существует множество других типов симметрий, которым должны соответствовать физические законы. Относительность по Галиею требует, чтобы физические законы движения оставались неизменными, независимо от того неподвижен объект, или двигается с постоянной скоростью. Специальная теория относительности утверждает, что законы движения должны оставаться прежними, даже если объект движется со скоростью, близкой к скорости света. Общая теория относительности говорит, что законы остаются прежними, даже если объект движется с ускорением.
Физики обобщали понятие симметрии по-разному: локальная симметрия, глобальная симметрия, непрерывная симметрия, дискретная симметрия и т.д. Виктор Стенджер объединил множество видов симметрии по тем, что мы называем инвариантность по отношению к наблюдателю (point of view invariance). Это означает, что законы физики должны оставаться неизменными, независимо от того, кто и как их наблюдает. Он показал как много областей современной физики (но не все) могут быть сведены к законам, удовлетворяющими инвариантности по отношению к наблюдателю. Это означает, что явления, относящиеся к одному феномену, связанны, несмотря на то, что они могут рассматриваться по-разному.
Понимание настоящей важности симметрии прошло с теорией относительности Эйнштейна. До него люди сначала открывали какой-то физический закон, а потом находили в нем свойство симметрии. Эйнштейн же использовал симметрию, чтобы найти закон. Он постулировал, что закон должен быть одинаков для неподвижного наблюдателя и для наблюдателя, двигающегося со скоростью, близкой к световой. С этим предположением, он описал уравнения специальной теории относительности. Это была революция в физике. Эйнштейн понял, что симметрия — определяющая характеристика законы природы. Не закон удовлетворяет симметрии, а симметрия порождает закон.
В 1918 году Эмми Нётер показала, что симметрия ещё более важное понятие в физике, чем думали до этого. Она доказала теорему, связывающую симметрии с законами сохранения. Теорема показала, что каждая симметрия порождает свой закон сохранения, и наоборот. Например инвариантность по смещению в пространстве порождает закон сохранения линейного импульса. Инвариантность по времени порождает закон сохранения энергии. Инвариантность по ориентации порождает закон сохранения углового момента. После этого физики стали искать новые виды симметрий, чтобы найти новые законы физики.
Таким образом мы определили что называть физическим законом. С этой точки зрения неудивительно, что эти законы кажутся нам объективными, вневременными, независимыми от человека. Так как они инвариантны по отношению к месту, времени, и взгляду на них человека, создается впечатление, что они существуют «где-то там». Однако на это можно посмотреть и по-другому. Вместо того, чтобы говорить, что мы смотрим на множество различных следствий из внешних законов, мы можем сказать, что человек выделил какие-то наблюдаемые физические явления, нашел в них что-то похожее и объединил их в закон. Мы замечаем только то, что воспринимаем, называем это законом и пропускаем все остальное. Мы не можем отказаться от человеческого фактора в понимании законов природы.
Прежде чем мы двинемся дальше, нужно упомянуть о одной симметрии, которая настолько очевидная, что о ней редко когда упоминают. Закон физики должен обладать симметрией по приложению (symmetry of applicability). То есть если закон работает с объектом одного типа, то он будет работать и с другим объектом такого же типа. Если закон верен для одной положительно заряженной частицы, двигающейся со скоростью, близкой к скорости света, то он будет работать и для другой положительно заряженной частицы, двигающейся со скоростью такого же порядка. С другой стороны, закон может не работать для макрообъектов с малой скоростью. Все похожие объекты связанны с одним законом. Нам понадобится этот вид симметрии, когда мы будем обсуждать связь математики с физикой.
Что есть математика
Давайте потратим немного времени на то, чтобы понять самую суть математики. Мы рассмотрим 3 примера.
Давным давно какой-то фермер обнаружил, что если ты возьмешь девять яблок и соединишь их с четырьмя яблоками, то в итоге ты получишь тринадцать яблок. Некоторое время спустя он обнаружил, что если девять апельсинов соединить с четырьмя апельсинами, то получится тринадцать апельсинов. Это означает, что если он обменяет каждое яблоко на апельсин, то количество фруктов останется неизменным. В какое-то время математики накопили достаточно опыта в подобных делах и вывели математическое выражение 9 + 4 = 13. Это маленькое выражение обобщает все возможные случаи таких комбинаций. То есть оно истинно для любых дискретных объектов, которые можно обменять на яблоки.
Более сложный пример. Одна из важнейших теорем алгебраической геометрии — теорема Гильберта о нулях (https://ru.wikipedia.org/wiki/Теорема_Гильберта_о_нулях ). Она заключается в том, что для каждого идеала J в полиномиальном кольце существует соответствующее алгебраическое множество V(J), а для каждого алгебраического множества S существует идеал I(S). Связь этих двух операций выражается как , где
— радикал идеала. Если мы заменим одно алг. мн-во на другое, мы получим другой идеал. Если мы заменим один идеал на другой, мы получим другое алг. мн-во.
Одним из основных понятий алгебраической топологии является гомоморфизм Гуревича. Для каждого топологического пространства X и положительного k существует группа гомоморфизмов из k-гомотопичой группы в k-гомологичную группу. . Этот гомоморфизм обладает особым свойством. Если пространство X заменить на пространство Y, а
заменить на
, то гомоморфизм будет другим
. Как и в предыдущем примере, какой-то конкретный случай этого утверждения не имеет большого значения для математики. Но если мы собираем все случаи, то мы получаем теорему.
В этих трех примерах мы смотрели на изменение семантики математических выражений. Мы меняли апельсины на яблоки, мы меняли одну идею на другую, мы заменяли одно топологическое пространство на другое. Главное в этом то, что делая правильную замену, математическое утверждение остается верным. Мы утверждаем, что именно это свойство является основным свойством математики. Так что мы будем называть утверждение математическим, если мы можем изменить то, на что оно ссылается, и при этом утверждение останется верным.
Теперь к каждому математическому утверждению нам нужно будет приставить область применения. Когда математик говорит «для каждого целого n», «Возьмем пространство Хаусдорфа», или «пусть C — кокуммутативная, коассоциативная инволютивная коалгебра», он определяет область применения для своего утверждения. Если это утверждение правдиво для одного элемента из области применения, то оно правдиво для каждого (при условии правильного выбора этой самой области применения, прим. пер.).
Эта замена одного элемента на другое, может быть описана как одно из свойств симметрии. Мы называем это симметрия семантики. Мы утверждаем, что эта симметрия фундаментальна, как для математики, так и для физики. Таким же образом, как физики формулируют свои законы, математики формулируют свои математические утверждения, одновременно определяя в какой области применения утверждение сохраняет симметрию семантики (иными словами где это утверждение работает). Зайдем дальше и скажем, что математическое утверждение — утверждение, которое удовлетворяет симметрии семантики.
Если среди вас найдутся логики, то им понятие симметрии семантики будет вполне очевидно, ведь логическое высказывание истинно, если оно истинно для каждой интерпретации логической формулы. Здесь же мы говорим, что мат. утверждение верно, если оно верно для каждого элемента из области применения.
Кто-то может возразить, что такое определение математики слишком широкое и что утверждение, удовлетворяющее симметрии семантики — просто утверждение, не обязательно математическое. Мы ответим, что во-первых, математика в принципе достаточно широка. Математика — это не только разговоры о числах, она о формах, высказываниях, множествах, категориях, микросостояниях, макросостояниях, свойствах и т.п. Чтобы все эти объекты были математическими, определение математики должно быть широким. Во-вторых, существует множество утверждений, не удовлетворяющих симметрии семантики. «В Нью-Йорке в январе холодно», «Цветы бывают только красными и зелеными», «Политики — честные люди». Все эти утверждения не удовлетворяют симметрии семантики и, следоваиельно, не математические. Если есть контрпример из области применения, то утверждение автоматически перестает быть математическим.
Математические утверждения удовлетворяют также и другим симметриям, например симметрии синтаксиса. Это означает, что одни и те же математические объекты могут быть представлены по-разному. Например число 6 может быть представлено как «2 * 3», или «2 + 2 + 2», или «54/9». Также мы можем говорить о «непрерывной самонепересекающийся кривой», о «простой замкнутой кривой», о «жордановой кривой», и мы будем иметь в виду одно и то же. На практике математики пытаются использовать наиболее простой синтаксис (6 вместо 5+2-1).
Некоторые симметрические свойства математики кажутся настолько очевидными, что о них вообще не говорят. Например математическая истина инвариантна по отношению ко времени и пространству. Если утверждение истинно, то оно будет истинно также завтра в другой части земного шара. Причем неважно, кто его произнесет — мать Тереза или Альберт Эйнштейн, и на каком языке.
Так как математика удовлетворяет всем этим типам симметрии, легко понять почему нам кажется, что математика (как и физика) объективна, работает вне времени и независима от наблюдений человека. Когда математические формулы начинают работать для совершенно разных задач, открытых независимо, иногда в разных веках, начинает казаться, что математика существует «где-то там». Однако, симметрия семантики (а это именно то, что происходит) — это фундаментальная часть математики, определяющая её. Вместо того, чтобы сказать, что существует одна математическая истина и мы лишь нашли несколько её случаев, мы скажем, что существует множество случаев математических фактов и человеческий разум объединил их вместе, создав математическое утверждение.
Почему математика хороша в описании физики?
Ну что, теперь мы можем задаться вопросов почему математика так хорошо описывает физику. Давайте взглянем на 3 физических закона.
В каждом из трех приведенных примеров физические законы естественно выражаются только через математические формулы. Все физические явления, которые мы хотим описать, находятся внутри математического выражения (точнее в частных случаях этого выражения). В терминах симметрий мы говорим, что физическая симметрия применимости — частный случай математической симметрии семантики. Более точно, из симметрии применимости следует, что мы можем заменить один объект на другой (того же класса). Значит математическое выражение, которое описывает явление, должно обладать таким же свойством (то есть его область применения должна быть хотя бы не меньше).
Иными словами, мы хотим сказать, что математика так хорошо работает в описании физических явлений, потому-что физика с математикой формировались одинаковым образом. Законы физики не находятся в платоновом мире и не являются центральными идеями в математике. И физики, и математики выбирают свои утверждения таким образом, чтобы они подходили ко многим контекстам. В этом нет ничего странного, что абстрактные законы физики берут свое начало в абстрактном языке математики. Как и в том, что некоторые математические утверждения сформулированы задолго до того, как были открыты соответствующие законы физики, ведь они подчиняются одним симметриям.
Теперь мы полностью решили загадку эффективности математики. Хотя, конечно, есть ещё множество вопросов, на которые нет ответов. Например, мы можем спросить почему у людей вообще есть физика и математика. Почему мы способны замечать симметрии вокруг нас? Частично ответ на этот вопрос в том, что быть живым — значит проявлять свойство гомеостазиса, поэтому живые существа должны защищаться. Чем лучше они понимают своё окружение, тем лучше они выживают. Неживые объекты, например камни и палки, никак не взаимодействуют со своим окружением. Растения же, с другой стороны, поворачиваются к солнцу, а их корни тянутся к воде. Более сложное животное может замечать больше вещей в своем окружении. Люди замечают вокруг себя множество закономерностей. Шимпанзе или, например, дельфины не могут этого. Закономерности наших мыслей мы называем математикой. Некоторые из этих закономерностей являются закономерностями физических явлений вокруг нас, и мы называем эти закономерности физикой.
Можно задаться вопросом почему в физических явлениях вообще есть какие-то закономерности? Почему эксперимент проведенный в Москве даст такие же результаты, если его провести в Санкт-Петербурге? Почему отпущенный мячик будет падать с одинаковой скоростью, несмотря на то, что его отпустили в другое время? Почему химическая реакция будет протекать одинаково, даже если на неё смотрят разные люди? Чтобы ответить на эти вопросы мы можем обратиться к антропному принципу. Если бы во вселенной не было каких-то закономерностей, то нас бы не существовало. Жизнь пользуется тем фактом, что у природы есть какие-то предсказуемые явления. Если бы вселенная была полностью случайна, или похожа на какую-то психоделическую картину, то никакая жизнь, по крайней мере интеллектуальная жизнь, не смогла бы выжить. Антропный принцип, вообще говоря, не решает поставленную проблему. Вопросы типа «Почему существует вселенная», «Почему есть что-то» и «Что тут вообще происходит» пока остаются без ответа.
Несмотря на то, что мы не ответили на все вопросы, мы показали, что наличие структуры в наблюдаемой вселенной вполне естественно описывается на языке математики.