Что изучает классическая механика
Классическая механика
Вы будете перенаправлены на Автор24
Классическая механика – это раздел классической физики, изучающий механическое движение макроскопических объектов, которые движутся со скоростями много меньше скорости света ( =3 108 м/с). Под макроскопическими объектами понимаются объекты, размеры которых м. (размер типичной молекулы).
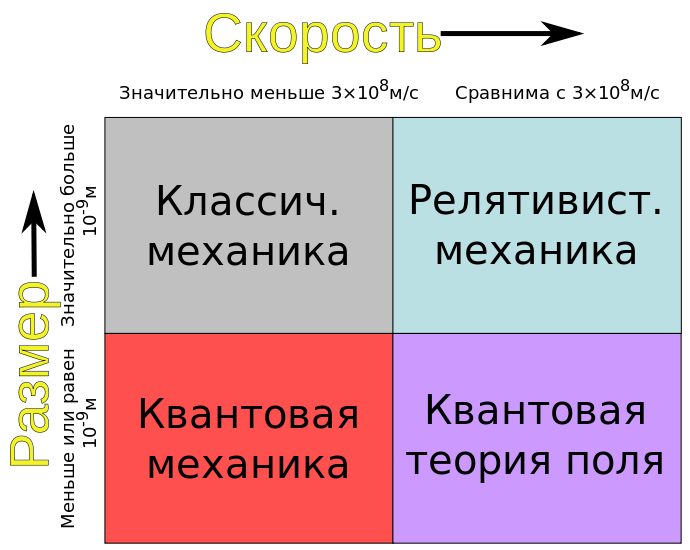
Место классической механики в системе физических наук и границы её применимости показаны на рисунке 1.
Рисунок 1. Область применимости классической механики
Классическая механика подразделяется на статику (которая рассматривает равновесие тел), кинематику (которая изучает геометрическое свойство движения без рассмотрения его причин) и динамику (которая рассматривает движение тел с учётом вызывающих его причин).
Существует несколько эквивалентных способов формального математического описания классической механики: законы Ньютона, Лагранжев формализм, Гамильтонов формализм, формализм Гамильтона — Якоби.
Когда классическая механика применяется к телам, скорости которых много меньше скорости света, а размеры значительно превышают размеры атомов и молекул, и при расстояниях или условиях, когда скорость распространения гравитации можно считать бесконечной, она даёт исключительно точные результаты. Потому и сегодня классическая механика сохраняет своё значение, поскольку она намного проще в понимании и использовании, чем остальные теории, и достаточно хорошо описывает повседневную реальность. Классическую механику можно использовать для описания движения очень широкого класса физических объектов: и обыденных объектов макромира (таких, как волчок и бейсбольный мяч), и объектов астрономических размеров (таких, как планеты и звёзды), и многих микроскопических объектов.
Классическая механика – древнейшая из физических наук. Ещё в доантичные времена люди не только опытным путём осознавали законы механики, но и применяли их на практике, конструируя простейшие механизмы. Уже в эпоху неолита и бронзового века появилось колесо, несколько позже применяются рычаг и наклонная плоскость. В античный период накопленные практические знания начали обобщаться, были сделаны первые попытки определить основные понятия механики, такие как сила, сопротивление, перемещение, скорость, и сформулировать некоторые её законы. Именно в ходе развития классической механики закладывались основы научного метода познания, предполагающего некие общие правила научных рассуждений об эмпирически наблюдаемых явлениях, выдвижения предположений (гипотез), эти явления объясняющих, построения моделей, упрощающих изучаемые явления при сохранении существенных их свойств, формирования систем идей ли принципов (теорий) и их математической интерпретации.
Однако качественная формулировка законов механики началась только в XVII веке н. э., когда Галилео Галилей открыл кинематический закон сложения скоростей и установил законы свободного падения тел. Через несколько десятилетий после Галилея Исаак Ньютон сформулировал основные законы динамики. В механике Ньютона движение тел рассматривается при скоростях, много меньше скорости света в пустоте. Ее называют классической или ньютоновской механикой в отличие от релятивистской механики, созданной в начале XX века, главным образом благодаря работам Альберта Эйнштейна.
Современная классическая механика в качестве метода исследования природных явлений использует их описание с помощью системы основных понятий и построения на их основе идеальных моделей реальных явлений и процессов.
Основы механики для чайников. Введение
В рамках любого учебного курса изучение физики начинается с механики. Не с теоретической, не с прикладной и не вычислительной, а со старой доброй классической механики. Эту механику еще называют механикой Ньютона. По легенде, ученый гулял по саду, увидел, как падает яблоко, и именно это явление подтолкнуло его к открытию закона всемирного тяготения. Конечно, закон существовал всегда, а Ньютон лишь придал ему понятную для людей форму, но его заслуга – бесценна. В данной статье мы не будем расписывать законы Ньютоновской механики максимально подробно, но изложим основы, базовые знания, определения и формулы, которые всегда могут сыграть Вам на руку.
Механика – раздел физики, наука, изучающая движение материальных тел и взаимодействия между ними.
Почему изучение физики начинается именно с механики? Потому что это совершенно естественно, не с термодинамического же равновесия его начинать?!
Механика – одна из старейших наук, и исторически изучение физики началось именно с основ механики. Помещенные в рамки времени и пространства, люди, по сути, никак не могли начать с чего-то другого, при всем желании. Движущиеся тела – первое, на что мы обращаем свое внимание.
Что такое движение?
Механическое движение – это изменение положения тел в пространстве относительно друг друга с течением времени.
Именно после этого определения мы совершенно естественно приходим к понятию системы отсчета. Изменение положения тел в пространстве относительно друг друга. Ключевые слова здесь: относительно друг друга. Ведь пассажир в машине движется относительно стоящего на обочине человека с определенной скоростью, и покоится относительно своего соседа на сиденье рядом, и движется с какой-то другой скоростью относительно пассажира в машине, которая их обгоняет.
Механика, как наука, имеет свою задачу. Задача механики – в любой момент времени знать положение тела в пространстве. Иными словами, механика строит математическое описание движения и находит связи между физическими величинами, его характеризующими.
Для того, чтобы двигаться далее, нам понадобится понятие “материальная точка”. Говорят, физика – точная наука, но физикам известно, сколько приближений и допущений приходится делать, чтобы согласовать эту самую точность. Никто никогда не видел материальной точки и не нюхал идеального газа, но они есть! С ними просто гораздо легче жить.
Материальная точка – тело, размерами и формой которого в контексте данной задачи можно пренебречь.
Разделы классической механики
Механика состоит из нескольких разделов
Кинематика с физической точки зрения изучает, как именно тело движется. Другими словами, этот раздел занимается количественными характеристиками движения. Найти скорость, путь – типичные задачи кинематики
Динамика решает вопрос, почему оно движется именно так. То есть, рассматривает силы, действующие на тело.
Статика изучает равновесие тел под действием сил, то есть отвечает на вопрос: а почему оно вообще не падает?
Границы применимости классической механики
Классическая механика уже не претендует на статус науки, объясняющей все (в начале прошлого века все было совершенно иначе), и имеет четкие рамки применимости. Вообще, законы классической механики справедливы привычном нам по размеру мире (макромир). Они перестают работать в случае мира частиц, когда на смену классической приходит квантовая механика. Также классическая механика неприменима к случаям, когда движение тел происходит со скоростью, близкой к скорости света. В таких случаях ярко выраженными становятся релятивистские эффекты. Грубо говоря, в рамках квантовой и релятивистской механики – классическая механика, это частный случай, когда размеры тела велики, а скорость – мала.
Движение на скорости, близкой к скорости света, нельзя описать законами классической механики
Вообще говоря, квантовые и релятивистские эффекты никогда никуда не деваются, они имеют место быть и при обычном движении макроскопических тел со скоростью, много меньшей скорости света. Другое дело, что действие этих эффектов так мало, что не выходит за рамки самых точных измерений. Классическая механика, таким образом, никогда не потеряет своей фундаментальной важности.
Мы продолжим изучение физических основ механики в следующих статьях. Для лучшего понимания механики Вы всегда можете обратиться к нашим авторам, которые в индивидуальном порядке прольют свет на темное пятно самой сложной задачи.
Классическая механика
| Фундаментальные понятия |
|---|
| Пространство · Время · Масса · Сила Энергия · Импульс |
| Формулировки |
|---|
| Ньютоновская механика Лагранжева механика Гамильтонова механика Формализм Гамильтона — Якоби |
| Разделы |
|---|
| Прикладная механика Небесная механика Механика сплошных сред Геометрическая оптика Статистическая механика |
| Учёные |
|---|
| Галилей · Кеплер · Ньютон Эйлер · Лаплас · Д’Аламбер Лагранж · Гамильтон · Коши |
Класси́ческая меха́ника — вид механики (раздела физики, изучающего законы изменения положений тел в пространстве со временем и причины, это вызывающие), основанный на законах Ньютона и принципе относительности Галилея. Поэтому её часто называют «Ньютоновской механикой».
Классическая механика подразделяется на:
Существует несколько эквивалентных способов формального математического описания классической механики:
Классическая механика даёт очень точные результаты, если её применение ограничено телами, скорости которых много меньше скорости света, а размеры значительно превышают размеры атомов и молекул. Обобщением классической механики на тела, двигающиеся с произвольной скоростью, является релятивистская механика, а на тела, размеры которых сравнимы с атомными — квантовая механика. Квантовая теория поля рассматривает квантовые релятивистские эффекты.
Тем не менее, классическая механика сохраняет своё значение, поскольку:
Классическую механику можно использовать для описания движения таких объектов, как волчок и бейсбольный мяч, многих астрономических объектов (таких, как планеты и галактики), и иногда даже многих микроскопических объектов, таких как молекулы.
Классическая механика является самосогласованной теорией, то есть в её рамках не существует утверждений, противоречащих друг другу. Однако, её объединение с другими классическими теориями, например классической электродинамикой и термодинамикой приводит к появлению неразрешимых противоречий. В частности, классическая электродинамика предсказывает, что скорость света постоянна для всех наблюдателей, что несовместимо с классической механикой. В начале XX века это привело к необходимости создания специальной теории относительности. При рассмотрении совместно с термодинамикой, классическая механика приводит к парадоксу Гиббса, в котором невозможно точно определить величину энтропии, и к ультрафиолетовой катастрофе, в которой абсолютно чёрное тело должно излучать бесконечное количество энергии. Попытки разрешить эти проблемы привели к возникновению и развитию квантовой механики.
Содержание
Основные понятия
Классическая механика оперирует несколькими основными понятиями и моделями. Среди них следует выделить:
Основные законы
Принцип относительности Галилея
Законы Ньютона
Основой классической механики являются три закона Ньютона.
Первый закон устанавливает наличие свойства инертности у материальных тел и постулирует наличие таких систем отсчёта, в которых движение свободного тела происходит с постоянной скоростью (такие системы отсчёта называются инерциальными).
Второй закон Ньютона вводит понятие силы как меры взаимодействия тела и на основе эмпирических фактов постулирует связь между величиной силы, ускорением тела и его инертностью (характеризуемой массой). В математической формулировке второй закон Ньютона чаще всего записывается в следующем виде:
где 

Второй закон Ньютона может быть также записан в терминах изменения импульса тела 
В такой форме закон справедлив и для тел с переменной массой, а также в релятивистской механике.
Второго закона Ньютона недостаточно для описания движения частицы. Дополнительно требуется описание силы 
Третий закон Ньютона уточняет некоторые свойства введёного во втором законе понятия силы. Им постулируется наличие для каждой силы, действующей на первое тело со стороны второго, равной по величине и противоположной по направлению силы, действующей на второе тело со стороны первого. Наличие третьего закона Ньютона обеспечивает выполнение закона сохранения импульса для системы тел.
Закон сохранения импульса
Закон сохранения энергии
За пределами применимости законов Ньютона
Классическая механика также включает в себя описания сложных движений протяжённых неточечных объектов. Законы Эйлера обеспечивают расширение законов Ньютона на эту область. Понятие угловой момент опирается на те же математические методы, используемые для описания одномерного движения.
Уравнения движение ракеты расширяют понятие скорости, когда импульса объекта меняется со временем, чтобы учесть такой эффект как потеря массы. Есть две важные альтернативные формулировки классической механики: механика Лагранжа и Гамильтонова механика. Эти и другие современные формулировки, как правило, обходят понятие «сила», и делают упор на другие физические величины, такие как энергия или действие, для описания механических систем.
Приведенные выше выражения для импульса и кинетической энергии действительны только при отсутствии значительного электромагнитного вклада. В электромагнетизме, второй закон Ньютона для провода с током нарушается, если не включает в себя вклад электромагнитного поля в импульс системы выраженный через вектор Пойнтинга поделённый на c2, где c — это скорость света в свободном пространстве.
История
Древнее время
Классическая механика зародилась в древности главным образом в связи с проблемами, которые возникали при строительстве. Первым из разделов механики, получившим развитие стала статика, основы которой были заложены в работах Архимеда в III веке до н. э. Им были сформулированы правило рычага, теорема о сложении параллельных сил, введено понятие центра тяжести, заложены основы гидростатики (сила Архимеда).
Средние века
XIV веке французский философ Жан Буридан разработал теорию импетуса. В дальнейшем её развил ученик Жана — епископ Альберт Саксонский.
Новое время
XVII век
Динамика как раздел классической механики начал развиваться только в XVII веке. Его основы были заложены Галилео Галилеем, который первым правильно решил задачу о движении тела под действием заданной силы. На основе эмпирических наблюдений им были открыты закон инерции и принцип относительности. Помимо этого Галилеем внесён вклад в зарождение теории колебаний и науки о сопротивлении материалов.
Христиан Гюйгенс проводил исследования в области теории колебаний, в частности изучал движение точки по окружности, а также колебания физического маятника. В его работах были также впервые сформулированы законы упругого удара тел.
Заложение основ классической механики завершилось работами Исаака Ньютона, сформулировавшего в наиболее общей форме законы механики и открывшего закон всемирного тяготения. Им же в 1684 году был установлен закон вязкого трения в жидкостях и газах.
Так же в XVII веке в 1660 году был сформулирован закон упругих деформаций, носящий имя своего первооткрывателя Роберта Гука.
XVIII век
В XVIII веке зарождается и интенсивно развивается аналитическая механика. Её методы для задачи о движении материальной точки были разработаны Леонардом Эйлером, которые заложил основы динамики твёрдого тела. Эти методы основываются на принципе виртуальных перемещений и на принципе Д’Аламбера. Разработку аналитических методов завершил Лагранж, которому удалось сформулировать уравнения динамики механической системы в наиболее общем виде: с использованием обобщённых координат и импульсов. Помимо этого, Лагранж принял участие в заложении основ современной теории колебаний.
Альтернативный метод аналитической формулировки классической механики основывается на принципе наименьшего действия, который впервые был высказан Мопертюи по отношению к одной материальной точке и обобщён на случай системы материальных точек Лагранжем.
Так же в XVIII веке в работах Эйлера, Даниила Бернулли, Лагранжа и Д’Аламбера были разработаны основы теоретического описания гидродинамики идеальной жидкости.
XIX век
В XIX веке развитие аналитической механики происходит в работах Остроградского, Гамильтона, Якоби, Герца и др. В теории колебаний Раусом, Жуковским и Ляпуновым была разработана теория устойчивости механических систем. Кориолис разработал теорию относительного движения, доказав теорему о разложении ускорения на составляющие. Во второй половине XIX века происходит выделение кинематики в отдельный раздел механики.
Особенно значительны в XIX веке были успехи в области механики сплошной среды. Навье и Коши в общей форме сформулировали уравнения теории упругости. В работах Навье и Стокса были получены дифференциальные уравнения гидродинамики с учётом вязкости жидкости. Наряду с этим происходит углубление знаний в области гидродинамики идеальной жидкости: появляются работы Гельмгольца о вихрях, Кирхгофа, Жуковского и Рейнольдса о турбулентности, Прандтля о пограничных эффектах. Сен-Венан разработал математическую модель, описывающую пластические свойства металлов.
Новейшее время
В XX веке интерес исследователей переключается на нелинейные эффекты в области классической механики. Ляпунов и Анри Пуанкаре заложили основы теории нелинейных колебаний. Мещерский и Циолковский провели анализ динамики тел переменной массы. Из механики сплошной среды выделяется аэродинамика, основы которой разработаны Жуковским. В середине XX века активно развивается новое направление в классической механике — теория хаоса. Важными также остаются вопросы устойчивости сложных динамических систем.
Ограничения классической механики
Классическая механика дает точные результаты для систем, которые мы встречаем в повседневной жизни. Но её предсказания становятся некорректными для систем, скорость которых приближается к скорости света, где она заменяется релятивистской механикой или для очень малых систем, где действуют законы квантовой механики. Для систем, которые объединяют оба эти свойства, вместо классической механики применяется релятивистская квантовая теория поля. Для систем с очень большим количеством составляющих, или степеней свободы, классическая механика также не может быть адекватной, зато используются методы статистической механики.
Классическая механика является широко применяемой, потому что она, во-первых, гораздо проще и легче в применении, чем перечисленные выше теории, и, во-вторых, имеет большие возможности для аппроксимации и применения для очень широкого класса физических объектов, начиная с привычных, таких как волчок или мяч, до больших астрономических объектов (планеты, галактики) и совсем микроскопических (органические молекулы).
Хотя классическая механика является в целом совместимой с другими «классическими» теориями, такими как классическая электродинамика и термодинамика, имеются некоторые несоответствия между этими теориями, которые были найдены в конце 19 века. Они могут быть решены методами более современной физики. В частности, уравнения классической электродинамики неинвариантны относительно преобразований Галилея. Скорость света входит в них как константа, что означает, что классическая электродинамика и классическая механика могли бы быть совместимы только в одной избранной системе отсчета, связанной с эфиром. Однако, экспериментальная проверка не выявила существование эфира, что привело к созданию специальной теории относительности, в рамках которой были модифицированы уравнения механики. Принципы классической механики также несовместимы с некоторыми утверждениями классической термодинамики, что приводит к парадоксу Гиббса, согласно которому невозможно точно установить энтропию, и к ультрафиолетовой катастрофе, в которой абсолютно черное тело должно излучать бесконечное количество энергии. Для преодоления этих несовместимости была создана квантовая механика.
Классическая механика
Из Википедии — свободной энциклопедии
Класси́ческая меха́ника — вид механики (раздела физики, изучающего законы изменения положений тел в пространстве со временем и причины, его вызывающие), основанный на законах Ньютона и принципе относительности Галилея. Поэтому её часто называют «нью́тоновой меха́никой».
Классическая механика подразделяется на:
Существует несколько эквивалентных способов формального математического описания классической механики:
На рубеже XIX—XX вв. были выявлены пределы применимости классической механики. Выяснилось, что она даёт исключительно точные результаты, но только в тех случаях, когда применяется к телам, скорости которых много меньше скорости света, а размеры значительно превышают размеры атомов и молекул, и при расстояниях или условиях, когда скорость распространения гравитации можно считать бесконечной (обобщением классической механики на тела, двигающиеся с произвольной скоростью, является релятивистская механика, а на тела, размеры которых сравнимы с атомными, — квантовая механика; квантовые релятивистские эффекты рассматриваются квантовой теорией поля).
Тем не менее, классическая механика сохраняет своё значение, поскольку она:
Классическую механику можно использовать для описания движения очень широкого класса физических объектов: и обыденных предметов макромира (таких, как волчок и бейсбольный мяч), и объектов астрономических размеров (таких, как планеты и звёзды), и многих микроскопических объектов.
Классическая механика
| Классическая механика |
|---|
 Второй закон Ньютона |
Энергия · Импульс
Лагранжева механика
Гамильтонова механика
Небесная механика
Механика сплошных сред
Геометрическая оптика
Статистическая механика
Эйлер · Лаплас · Д’Аламбер
Лагранж · Гамильтон · Коши
Классическая механика подразделяется на:
Существует несколько эквивалентных способов формального математического описания классической механики:
На рубеже XIX—XX вв. были выявлены пределы применимости классической механики (см. раздел «Ограничения применимости классической механики» в конце статьи). Выяснилось, что она даёт исключительно точные результаты, но только в тех случаях, когда она применяется к телам, скорости которых много меньше скорости света, а размеры значительно превышают размеры атомов и молекул и при расстояниях или условиях, когда скорость распространения гравитации можно считать бесконечной (обобщением классической механики на тела, двигающиеся с произвольной скоростью, является релятивистская механика, а на тела, размеры которых сравнимы с атомными — квантовая механика; квантовые релятивистские эффекты рассматриваются квантовой теорией поля).
Тем не менее, классическая механика сохраняет своё значение, поскольку она:
Классическую механику можно использовать для описания движения очень широкого класса физических объектов: и обыденных объектов макромира (таких, как волчок и бейсбольный мяч), и объектов астрономических размеров (таких, как планеты и звёзды), и многих микроскопических объектов.
Содержание
Основные понятия
Классическая механика оперирует несколькими основными понятиями и моделями. Среди них следует выделить:
Основные законы
Принцип относительности Галилея
Законы Ньютона
Основой классической механики являются три закона Ньютона (формулируя данные законы, Ньютон применял термин «тело», хотя фактически речь в них идёт о материальных точках).
Первый закон устанавливает наличие свойства инертности у материальных тел и постулирует наличие таких систем отсчёта, в которых движение свободного тела происходит с постоянной скоростью (такие системы отсчёта называются инерциальными).
Второй закон Ньютона на основе эмпирических фактов постулирует связь между величиной силы, ускорением тела и его инертностью (характеризуемой массой). В математической формулировке второй закон Ньютона чаще всего записывается в следующем виде:
где 

Второй закон Ньютона может быть также записан в терминах изменения импульса материальной точки 
Второго закона Ньютона недостаточно для описания движения частицы. Дополнительно требуется описание силы 
Третий закон Ньютона уточняет некоторые свойства введённого во втором законе понятия силы. Им постулируется наличие для каждой силы, действующей на первое тело со стороны второго, равной по величине и противоположной по направлению силы, действующей на второе тело со стороны первого. Наличие третьего закона Ньютона обеспечивает выполнение закона сохранения импульса для системы тел.
Закон сохранения импульса
Закон сохранения энергии
Распространение на протяжённые тела
Классическая механика также включает в себя описание сложных движений протяжённых неточечных объектов. Распространение законов ньютоновой механики на такие объектов было в основном заслугой Эйлера. Современная формулировка законов Эйлера также использует аппарат трёхмерных векторов.
История
Древнее время
Средние века
Новое время
XVII век
Заложение основ классической механики завершилось работами Исаака Ньютона, сформулировавшего в наиболее общей форме законы механики и открывшего закон всемирного тяготения. Им же в 1684 году был установлен закон вязкого трения в жидкостях и газах.
XVIII век
Альтернативный метод аналитической формулировки классической механики основывается на принципе наименьшего действия, который впервые был высказан Мопертюи по отношению к одной материальной точке и обобщён на случай системы материальных точек Лагранжем.
XIX век
Новейшее время
Ограничения применимости классической механики
Область применимости классической механики.
Предсказания классической механики становятся неточными для систем, скорость которых приближается к скорости света (поведение таких систем должно описываться релятивистской механикой), или для очень малых систем, где действуют законы квантовой механики. Для описания поведения систем, в которых существенны и релятивистские, и квантовые эффекты, применяется релятивистская квантовая теория поля. Для систем с очень большим количеством составляющих, или степеней свободы, классическая механика также не может быть адекватной, и в этом случае используются методы статистической механики.
Классическая механика является самосогласованной теорией, т. е. в её рамках не существует утверждений, противоречащих друг другу. В целом она является совместимой и с другими «классическими» теориями (такими, как классическая электродинамика и классическая термодинамика), однако в конце XIX века выявились некоторые несоответствия между этими теориями; преодоление этих несоответствий знаменовало становление современной физики. В частности:
См. также
Примечания
Литература
Ссылки
Выделить Классическая механика и найти в: