Что изучает алгебра в 7 классе
Класс: 7
Презентация к уроку
Ход урока
Мы с вами уже полугодие изучаем новый предмет – алгебра, но я не случайно не отвечала вам подробно на вопрос – Что же такое алгебра? Что она изучает? А делала я это потому, что вы были еще не готовы, не хватало ваших знаний. Сегодня этот момент наступил. На уроке мы постараемся разобраться что изучает алгебра, что лежит в ее основе, заглянем в историю создания предмета.
Откройте тетради, запишите число и тему:
Что изучает алгебра? (слайд №1)
С чего начнем? Наверное, с названия (слайд №2)
По многим названиям предметов сразу становиться ясно, чем занимается данная наука.
| Геометрия – гео-земля метро-мерять Биология – био– жизнь логос-учение География – гео-земля графо – пишу |
А слово “Алгебра” или “Аль-джебр” в переводе с арабского означает
Стало понятно чем занимается алгебра?
Наверное, наоборот, вводит в замешательство.
Вот так и в древней Испании, которая долгое время была под арабским владычеством и, слыша слово “алгебраист” решили, что это слово относится к костоправам или по нашему к хирургам и это недоразумение вошло в книгу
Сервантеса “Дон Кихот” там есть такой фрагмент, когда главный герой Дон Кихот был ранен в одном из поединков, то он просит своего верного друга Санчо Панса привести к нему срочно алгебриста.
Кто-то из вас уже читал или смотрел фильм по этой книге?
Т.е. перевод названия нашего предмета ничего не прояснил.
Что ж, пойдем другим путем.
Посмотрим, что же лежит в основе алгебры? Или другими словами, на чем стоит этот предмет? …
А стоит он на четырех больших китах. (слайд №4)
Давайте познакомимся с этими китами поближе. (Слайд №5)
у= 4х – 6 у = – 5х + 0,3 у = 6,5х
F(х)= 4х 3 +3х у = 6,5х 2
у= 7 – 3х+ ln у = х 3 f(х) = х 2 +х-4
y = sin3x
На этом слайде вы видите надписи. Что это? (Функции)
Запишите в тетрадь. Это кит-функция. (Слайд №6)
– Какими способами можно задать функцию?
– С какими функциями мы уже знакомы?
Это огромный раздел нашего предмета Алгебры.
А сейчас задание по вариантам от первого кита-функции (слайд №7)
| Построить графики следующих функций на одних осях координат: | |
| 1 вариант; | |
Самостоятельная работа на 5 минут в тетради. Затем проверить (слайд №8) и (слайд №9) причем, ответы с ошибками. Должны заметить, что в 1 варианте не подписаны оси координат, а во 2 вар. не подписаны графики и ошибки исправить по щелчку мышкой
Мы познакомились с китом – Функция (слайд №10)
А что вы видите на спине второго кита? (слайд №11)

Sin 2 2x – 3cos2x = 0
Конечно, это уравнения. Только некоторые из них нам хорошо знакомы, а с остальными нам предстоит знакомство на протяжении учебы. Запишите в тетрадь кит-уравнение. (слайд №12)
– Что такое уравнение?
– Что значит решить уравнение?
Оказывается, благодаря решению уравнений, мы получили название нашего предмета – алгебра.
(слайд №13) Впервые это слово прозвучало в книге ученого 1 века нашей эры Мухаммед Бен Мусса Аль-Хорезми (787 – около 850)
Откройте ваши учебники на стр. 16.
(Алгебра 7 класс под редакцией С.А. Теляковского)
Название у нее было очень странное (слайд №14)
“Краткая книга об исчислении аль-джабры и аль-мукабалы”
В ней рассказывалось о том, как решаются уравнения. Причем этими правилами мы пользуемся и теперь
Слово “аль-джабра” видимо понравилось ученым и оно дало название нашему предмету
Задание от этого кита (слайд №15)
(Самостоятельно 5 минут. Проверить ответы по щелчку)
РЕШИТЕ УРАВНЕНИЯ:
1) 2у(3у – 7) – (7 – 3у) = 0;
2) 
1) 7х(8х – 3) – (3 – 8х) = 0
2)
(слайд №16) Посмотрите на третьего кита.
Что вы видите на его спине (слайд №17)
Значит третий кит называется Тождество. Запишите в тетрадь.
– А что такое тождество?
Кит Тождество приготовил работу на желтым карточках
Задание от кита “Тождество”
Выполните тождественные преобразования и упростите выражение:
Задание от кита “Тождество”
Выполните тождественные преобразования и упростите выражение:
2) (1-2а)(14-а)+а(а 2 +51)-2(а 2 +21)
Задание от кита “Тождество”
Выполните тождественные преобразования и упростите выражение:
Задание от кита “Тождество”
Выполните тождественные преобразования и упростите выражение:
Мы познакомились с тремя китами. (Слайд №20) С тремя основными разделами алгебры, а это самый старый и уважаемый. Без него не могут обходиться другие киты никак. Это кит – … (число) (слайд №21)
Задание от кита “ЧИСЛО”
Выполните действия в 2-х примерах:
Задание от кита “ЧИСЛО”
Выполните действия в 2-х примерах:
От него вам задание на оранжевой карточке (слайд №22), но коль это уважаемый кит и его решение не терпит суеты – выполните его дома, а завтра на уроке мы проверим, кроме этого (слайд №23) на домашнее задание пойдут следующие номера: №241, №366, №778.
А сейчас посчитайте сколько плюсов вы заработали
– Сколько плюсов-такая и оценка за работу на уроке. (слайд №24)
Подведение итогов. Выставление оценок за урок.
Для следующего урока. (Слайд №25)
Что изучает алгебра в 7 классе
Выражения и их преобразования
☑ 1. Степенью числа а с натуральным показателем n, большим 1, называют произведение n множителей, каждый из которых равен а: 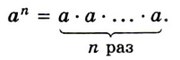
Степень числа а ≠ 0 с показателем 0 равна 1: а 0 = 1.
☑ 2. Свойства степеней с натуральными показателями:
а m • а n = а m+n
При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
(а m ) n = а mn
При возведении степени в степень основание оставляют прежним, а показатели перемножают.
(ab) n = а n b n
При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.
Степенью одночлена называют сумму показателей степеней всех переменных, входящих в одночлен. Например, степень одночлена –8а 2 b 4 равна 6.
☑ 4. Многочленом называют сумму одночленов. Например, 3х 5 – 4х 2 + 1, 7a 3 b – ab 2 + ab + 6 —многочлены. Одночлены считают многочленами, состоящими из одного члена.
Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Например, степень многочлена 5х 3 у + 3х 2 у 5 + ху равна степени одночлена 3х 2 у 5 , т. е. равна 7.
Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида.
☑ 5. При сложении многочленов пользуются правилом раскрытия скобок : если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки. Например,
(3аb + 5с 2 ) + (ab – с 2 ) = 3ab + 5с 2 + ab – с 2 = 4аb + 4с 2
При вычитании многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки. Например,
(6x 2 – у) – (2x 2 – 8у) = 6х 2 – у – 2х 2 + 8у = 4х 2 + 7у
Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить. Например,
а 2 (3аb – b 3 + 1) = 3а 3 b – а 2 b 3 + а 2
Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить. Например,
(5х – 1)(3х + 2) = 15x 2 – Зx + 10x – 2 = 15x 2 + 7x – 2
☑ 6. Формулы сокращённого умножения:
(а + b) 2 = а 2 + 2аb + b 2
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.
(а – b) 2 = а 2 – 2аb + b 2
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений, плюс квадрат второго выражения.
(а + b) 3 = а 3 + 3а 2 b + 3ab 2 + b 3
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(а – b) 3 = а 3 – 3а 2 b + Заb 2 – b 3
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(а – b)(а + b) = а 2 – b 2
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
а 3 + b 3 = (а + b)(a 2 – аb + b 2 )
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
а 3 – b 3 = (а – b)(a 2 + ab + b 2 )
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
☑ 7. Разложением многочлена на множители называют представление многочлена в виде произведения многочленов.
Для разложения многочленов на множители применяют вынесение общего множителя за скобки, группировку, формулы сокращённого умножения. Например, многочлен 5х 3 – х 2 у можно разложить на множители, вынеся за скобки х 2 :
Многочлен 3х – 3у – ах + ау можно разложить на множители, используя способ группировки:
3х – 3у – ах + ау = (3x – 3у) – (ах – ау) = 3(х – у) – а (х – у) = (х – у)(3 – а).
Многочлен а 4 – 25x 2 можно разложить на множители, используя формулу разности квадратов двух выражений:
а 4 – 25x 2 = (а 2 ) 2 – (5x) 2 = (а 2 – 5x)(а 2 + 5x).
Иногда многочлен удаётся разложить на множители, применив последовательно несколько способов.
Алгебра 7 класс Все формулы
Уравнения
Решить уравнение с одной переменной — значит найти все его корни или доказать, что корней нет.
☑ 9. Уравнения с одной переменной, имеющие одни и те же корни, называют равносильными. Например, уравнения x 2 = 25 и (х + 5)(х – 5) = 0 равносильны. Каждое из них имеет два корня: –5 и 5. Уравнения, не имеющие корней, также считают равносильными.
При решении уравнений с одной переменной используются следующие свойства:
Если а = 0 и b ≠ 0, то уравнение ах = b не имеет корней. Например, уравнение 0 • х = 7 не имеет корней.
Если а = 0 и b = 0, то корнем уравнения ах = b является любое число.
Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения с двумя переменными, не имеющие решений, также считают равносильными.
В уравнении с двумя переменными можно переносить слагаемые из одной части в другую, изменяя их знаки, и обе части уравнения можно умножать или делить на одно и то же число, не равное нулю. При этом получаются уравнения, равносильные исходному.
☑ 12. Линейным уравнением с двумя переменными называют уравнение вида ах + by = с, где х и у — переменные, а, b и с — числа.
☑ 13. Графиком уравнения с двумя переменными называют множество точек координатной плоскости, координаты которых являются решениями этого уравнения.
Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая.
☑ 14. Решением системы уравнений с двумя переменными называют пару значений переменных, обращающую каждое уравнение системы в верное равенство. Например, пара чисел х = 7, у = –1 — решение системы 
Решить систему уравнений — значит найти все её решения или доказать, что решений нет.
Системы уравнений с двумя переменными, имеющие одни и те же решения, называют равносильными. Системы, не имеющие решений, также считают равносильными.
☑ 15. Для решения систем линейных уравнений с двумя переменными используются графический способ, способ подстановки, способ сложения.
При графическом способе строят графики линейных уравнений (прямые) и анализируют их расположение:
При решении системы двух линейных уравнений с двумя переменными способом подстановки поступают следующим образом:
При решении системы двух линейных уравнений с двумя переменными способом сложения поступают следующим образом:
Алгебра 7 класс Все формулы
Функции
Независимую переменную иначе называют аргументом, а о зависимой переменной говорят, что она является функцией этого аргумента. Все значения, которые принимает независимая переменная, образуют область определения функции.
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
Графиком линейной функции у = kx + b является прямая. Число k называют угловым коэффициентом прямой, являющейся графиком функции у = kx + b.
Графики двух линейных функций пересекаются, если их угловые коэффициенты различны, и параллельны, если их угловые коэффициенты одинаковы.
Линейную функцию, задаваемую формулой у = kx при k ≠ 0, называют прямой пропорциональностью.
График прямой пропорциональности есть прямая, проходящая через начало координат. При k > 0 график расположен в первой и третьей координатных четвертях, а при k у = х 2 — парабола. Этот график проходит через начало координат и расположен в первой и второй координатных четвертях. Он симметричен относительно оси у.
График функции у = х 3 проходит через начало координат и расположен в первой и третьей координатных четвертях. Он симметричен относительно начала координат.
Статистические характеристики
☑ Средним арифметическим ряда чисел называют частное от деления суммы этих чисел на число слагаемых.
Модой ряда чисел называют число, которое встречается в данном ряду чаще других. Ряд чисел может иметь более одной моды или не иметь моды совсем.
Медианой упорядоченного ряда чисел с нечётным числом членов называют число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называют среднее арифметическое двух чисел, записанных посередине.
Например, медиана ряда чисел 17, 21, 27, 29, 32, 37, 41 равна 29, а медиана ряда чисел 28, 43, 54, 56, 58, 62 равна 55.
Медианой произвольного ряда чисел называют медиану соответствующего упорядоченного ряда.
Размахом ряда чисел называют разность между наибольшим и наименьшим из этих чисел.
Вы смотрели Конспект «Алгебра 7 класс Все формулы и определения» — краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского). Выберите дальнейшие действия:
Что изучает алгебра в 7 классе
(остальные материалы готовятся к публикации)
Глава 3. Алгебра 8 класс
(остальные материалы готовятся к публикации)
Глава 4. Алгебра 9 класс
(остальные материалы готовятся к публикации)
Глава 5. Материалы для подготовки к ОГЭ
Глава 6. Алгоритмы решения задач по алгебре
Электронные формы учебников для 6-9 классов (ссылки):
Алгебра (от араб. الْجَبْر, «аль-джабр» — восполнение) — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики. Слово «алгебpа» также употребляется в общей алгебре в названиях различных алгебраических систем. В более широком смысле под алгеброй понимают раздел математики, посвящённый изучению операций над элементами множества произвольной природы, обобщающий обычные операции сложения и умножения чисел.
Алгeбра как раздел математики традиционно включает следующие категории: Элементарная, Общая, Универсальная, Линейная (включая матрицы) и Алгебраическая комбинаторика.
Элементарная алгебpа, которая изучает свойства операций с вещественными числами. В ней постоянные и переменные обозначаются буквенными символами. Элементарная алгeбpа содержит правила преобразования математических выражений и уравнений с использованием этих символов. Обычно преподаётся в школе под названием aлгебра.
Источники идей и цитат для конспектов по Алгебре:
(с) Цитаты из вышеуказанных учебных пособий использованы на сайте в незначительных объемах, исключительно в учебных и информационных целях (пп. 1 п. 1 ст. 1274 ГК РФ).
Программа по математике. 7-й класс
Разделы: Математика
Класс: 7
Данная рабочая программа ориентирована на усвоение обязательного минимума математического образования, позволяет работать без перегрузок в классе с детьми разного уровня обучения и интереса к предмету. Она составлена на основе федерального компонента государственного стандарта основного общего образования (7 класс – 175 часов). Программа реализована в учебниках:
1. Алгебра, 7 кл.: Часть 1: Учебник для общеобразовательных учреждений/ А.Г. Мордкович – М.: Мнемозина, 2009.
2. Алгебра, 7 кл.: Часть 2: Задачник для общеобразовательных учреждений/ А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская – М.: Мнемозина, 2009.
Согласно федеральному базисному учебному плану на изучение математики в 7 классе отводится не менее 175 часов из расчета 5 ч в неделю, при этом разделение часов на изучение алгебры и геометрии может быть следующим:
5 часов в неделю алгебры в I четверть, 3 часа в неделю во II-IV четверти, итого 125 часов; 2 часа в неделю геометрии во II-IV четверти, итого 50 часов.
Уровень обучения – базовый.
Математическое образование в основной школе складывается из следующих содержательных компонентов: арифметика, алгебра, геометрия, элементы комбинаторики, элементы теории вероятностей, статистика и логика. В своей совокупности они отражают богатый опыт обучения математике в нашей стране.
В ходе освоения содержания курса учащиеся получают возможность:
– развить представление о месте и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
– овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
– изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
– развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
– получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
– развить логическое мышление речь – умение логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрции, интерпретации, аргументации и доказательства;
– сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Цели обучения математике:
– овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
– интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
– формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
– воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
В ходе преподавания математики следует обратить внимание на овладение умениями общеучебного характера, разнообразными способами деятельности, приобретение опыта:
– планирования и осуществления алгоритмической деятеьности;
– решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска путей и способов решения;
– исследовательской деятельности, развития идей, проведения экспериментов, обобщения;
– ясного, точного, грамотного изложения своих мыслей в устной и письменной речи;
– поиска, систематизации, анализа и классификации информации.
С учётом возрастных особенностей класса выстроена система уроков, спроектированы цели, задачи, ожидаемые (планируемые) результаты.
Основой целеполагания является обновление требований к уровню подготовки школьников в системе естественно-математического образовании, отражающее важнейшую особенность педагогической концепции государственного стандарта – переход от суммы «предметных результатов» к «межпредметным результатам». Такие результаты представляют собой обобщённые способы деятельности, которые отражают специфику не отдельных предметов, а ступеней общего образования. В государственном стандарте они зафиксированы как общие учебные умения, навыки и способы человеческой деятельности, что предполагает повышенное внимание к развитию межпредметных связей курса математики.
На ступени основной школы задачи учебных занятий определены как закрепление умений разделять процессы на этапы, звенья, выделять характерные причинно-следственные связи, определять структуру объекта познания, значимые функциональные связи и отношения между частями целого, сравнивать, сопоставлять, классифицировать, ранжировать объекты по одному или нескольким предложенным основаниям, критериям. Принципиальное значение в рамках курса приобретает умение различать факты, мнения, доказательства, гипотезы, аксиомы.
При выполнении творческих работ формируется умение определять адекватные способы решения учебной задачи на основе заданных алгоритмов, комбинировать известные алгоритмы деятельности в ситуациях, не предполагающих стандартного применения одного из них, мотивированно отказываться от образца деятельности, искать оригинальные решения.
Учащиеся должны приобрести умения по формированию собственного алгоритма решения познавательных задач, формулировать проблему и цели своей работы, определять адекватные способы и методы решения задачи, прогнозировать ожидаемый результат и сопоставлять его с собственными математическими знаниями. Учащиеся должны научиться представлять результаты индивидуальной и групповой познавательной деятельности в формах конспекта, реферата, рецензии.
Реализация календарно-тематического плана обеспечивает освоение общеучебных умений и компетенций в рамках информационно-коммуникативной деятельности:
– создание условия для умения логически обосновывать суждения, выдвигать гипотезы и понимать необходимость их проверки, ясно, точно и грамотно выражать свои мысли в устной и письменной речи;
– формирование умения использовать различные языки математики;
– создание условия для плодотворного участия в работе в группе, самостоятельной и мотивированной организации своей деятельности;
На уроках учащиеся могут более уверенно овладеть монологической и диалогической речью, умением вступать в речевое общение, участвовать в диалоге (понимать точку зрения собеседника, признавать право на иное мнение), приводить примеры, формулировать выводы.
Для решения познавательных и коммуникативных задач учащимся предлагается использовать различные источники информации.
Учащиеся должны уметь развёрнуто обосновывать суждения, давать определения, приводить доказательства (в том числе от противного), объяснять изученные положения на самостоятельно подобранных конкретных примерах, владеть основными видами публичных выступлений (высказывания, монолог, дискуссия, полемика), следовать этическим нормам и правилам ведения диалога, диспута. Предполагается простейшее использование учащимися мультимедийных ресурсов и компьютерных технологий для обработки, передачи, систематизации информации, создания базы данных, презентации результатов познавательной и практической деятельности. Стандарт ориентирован на воспитание школьника – гражданина и патриота России, развитие духовно-нравственного мира ученика, его национального самосознания. Эти положения нашли отражение в содержании уроков.
В процессе обучения у школьников должно быть сформировано умение формулировать свои мировоззренческие взгляды, и на этой основе будет осуществляться воспитание гражданственности и патриотизма.
В ходе освоения содержания курса алгебры учащиеся получают возможность:
– развить представление о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
– овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
– изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
– развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
– получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
– развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
– сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
В курсе геометрии 7 класса систематизируются знания обучающихся о простейших геометрических фигурах и их свойствах; вводится понятие равенства фигур; вводится понятие теоремы; вырабатывается умение доказывать равенство треугольников с помощью изученных признаков; вводится новый класс задач – на построение с помощью циркуля и линейки; вводится одно из важнейших понятий – понятие параллельных прямых; даётся первое представление об аксиомах и аксиоматическом методе в геометрии; вводится аксиома параллельных прямых; рассматриваются новые интересные и важные свойства треугольников (в данной теме доказывается одна из важнейших теорем геометрии — теорема о сумме углов треугольника. Она позволяет дать классификацию треугольников по углам (остроугольный, прямоугольный, тупоугольный), а также установить некоторые свойства и признаки равенства прямоугольных треугольников).
ОСНОВНОЕ СОДЕРЖАНИЕ (Алгебра)
Глава 1. Математический язык. Математическая модель (8 ч.)
Числовые и алгебраические выражения. Математический язык. Математическая модель. Линейное уравнение с одной переменной. Координатная прямая.
Основная цель: Повторить известные из курса математики 5-6 классов понятия числового и алгебраического выражений, дать учащимся общие представления о том, чем им предстоит заниматься в курсе алгебры, познакомить с тремя этапами математического моделирования при описании реальной ситуации на математическом языке: составление математической модели, работа с составленной моделью, ответ на вопрос задачи. Закрепить ранее приобретённые умения выполнять действия с рациональными числами и простейшие преобразования выражений, решать несложные уравнения, использовать аппарат уравнений для решения текстовых задач.
Глава 2. Линейная функция (17 ч.)
Координатная плоскость. Линейное уравнение с двумя переменными и его график. Линейная функция и её график. Линейная функция у = кх. Взаимное расположение графиков линейных функций.
Основная цель: Напомнить учащимся понятия координатной прямой и координатной плоскости, алгоритмы отыскания координат точки и точки по координатам, ввести числовые промежутки (отрезки, интервалы, лучи) и дать их различные интерпретации (вербальную, аналитическую, геометрическую), ввести понятия линейного уравнения с двумя переменными и его графика, линейной функции и прямой пропорциональности; на примере линейной функции, которая вводится как частный случай линейного уравнения с двумя переменными, познакомить учащихся (на наглядно-интуитивном уровне) с первыми свойствами функций: наибольшее и наименьшее значение на промежутке, возрастание и убывание.
Глава 3. Системы двух линейных уравнений с двумя переменными (14 ч.)
Основные понятия. Метод подстановки. Метод алгебраического сложения. Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций.
Глава 4. Степень с натуральным показателем и ее свойства (11 ч.)
Степень с натуральным показателем. Таблица основных степеней. Свойства степени с натуральными показателями. Умножение и деление степеней с одинаковыми показателями. Степень с нулевым показателем.
Основная цель: Ввести понятие степени с целым неотрицательным показателем, познакомить учащихся со свойствами степеней, привести первые образцы строгих математических рассуждений. Дать определение степени с натуральным показателем. При вычислении значений выражений, содержащих степени, следует обратить внимание на порядок действий. Обоснование свойств степеней позволяет познакомить учащихся с доказательствами, проводимыми на алгебраическом материале.
Глава 5. Одночлены. Арифметические операции одночленами (9 ч.)
Одночлен. Стандартный вид одночлена. Сложение и вычитание одночленов. Умножение одночленов. Возведение одночлена в натуральную степень. Деление одночлена на одночлен.
Основная цель: Ввести понятия одночлена, стандартного вида одночлена, подобных одночленов, научить школьников выполнять арифметические операции над одночленами.
Глава 6. Многочлены. Арифметические операции над многочленами (18 ч.)
Многочлен. Сложение и вычитание многочленов. Умножение многочлена на одночлен. Умножение многочлена на многочлен. Формулы сокращённого умножения. Деление многочлена на одночлен.
Глава 7. Разложение многочленов на множители (21 ч.)
Вынесение общего множителя за скобки. Способ группировки. Разложение многочленов на множители с помощью формул сокращённого умножения. Разложение многочленов на множители с помощью комбинации различных приёмов. Окращение алгебраических дробей. Тождества.
Основная цель: Объяснить учащимся, в чем состоит цель разложения многочлена на множители, познакомить их с основными приемами разложения многочлена на множители. Хотя тема «Алгебраические дроби» изучается в 8 классе, здесь учащиеся опережающим образом знакомятся с сокращением алгебраических дробей, чтобы процедура разложения многочлена на множители перестала быть целью, а превратилась в средство для решения других задач. Серьёзное внимание следует уделить разложению многочленов на множители с помощью вынесения за скобки общего множителя и с помощью группировки. Использование рассматриваемых преобразований можно встретить при решении различных задач, прежде всего при решении уравнений. Изучение многочленов завершить материалом обобщающего характера: введением понятия целого выражения, решением комбинированных упражнений на преобразование целого выражения в многочлен и на разложение на множители.
Глава 8. Функция у=х 2 (10 ч.)
Функция у=х 2 . Графическое решение уравнений. Запись у = f(х).
Основная цель: Дать учащимся представление о том, что в математике, кроме линейных функций, встречаются и другие функции, например, у=х 2 и кусочные функции; познакомить учащихся еще с двумя свойствами функций (на наглядно-интуитивном уровне): непрерывность функции, область определения функции; показать, как можно использовать графики функций для решения уравнений.
Обобщающее повторение (7 ч.)
Основная цель – сконцентрировать внимание учащихся на узловых вопросах учебного материала, обобщить и систематизировать сведения по всему курсу данной программы. Рассмотреть решение заданий комбинированного типа, задач эвристического характера и задач повышенной сложности.
Глава 1. Начальные геометрические сведения (7 часов)
Простейшие геометрические фигуры: прямая, точка, отрезок, луч, угол. Понятие равенства геометрических фигур. Сравнение отрезков и углов. Измерение отрезков, длина отрезка. Измерение углов, градусная мера угла. Смежные и вертикальные углы, их свойства. Перпендикулярные прямые.
Основная цель: систематизировать знания обучающихся о простейших геометрических фигурах и их свойствах; ввести понятие равенства фигур. В данной теме вводятся основные геометрические понятия и свойства простейших геометрических фигур на основе наглядных представлений обучающихся путем обобщения очевидных или известных из курса математики 1–6 классов геометрических фактов. Понятие аксиомы на начальном этапе обучения не вводится, и сами аксиомы не формулируются в явном виде. Необходимые исходные положения, на основе которых изучаются свойства геометрических фигур, приводятся в описательной форме. Принципиальным моментом данной темы является введение понятия равенства геометрических фигур на основе наглядного понятия наложения. Определенное внимание должно уделяться практическим приложениям геометрических понятий.
Глава 2. Треугольники (15 часов)
Треугольник. Признаки равенства треугольников. Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника. Равнобедренный треугольник и его свойства. Задачи на построение с помощью циркуля и линейки.
Основная цель: ввести понятие теоремы; выработать умение доказывать равенство треугольников с помощью изученных признаков; ввести новый класс задач — на построение с помощью циркуля и линейки. Признаки равенства треугольников являются основным рабочим аппаратом всего курса геометрии. Доказательство большей части теорем курса и также решение многих задач проводится по следующей схеме: поиск равных треугольников — обоснование их равенства с помощью какого-то признака – следствия, вытекающие из равенства треугольников. Применение признаков равенства треугольников при решении задач дает возможность постепенно накапливать опыт проведения доказательных рассуждений. На начальном этапе изучения и применения признаков равенства треугольников целесообразно использовать задачи с готовыми чертежами.
Глава 3. Параллельные прямые (9 часов)
Признаки параллельности прямых. Аксиома параллельных прямых. Свойства параллельных прямых.
Основная цель: ввести одно из важнейших понятий – понятие параллельных прямых; дать первое представление об аксиомах и аксиоматическом методе в геометрии; ввести аксиому параллельных прямых. Признаки и свойства параллельных прямых, связанных с углами, образованными при пересечении двух прямых секущей (накрест лежащими, односторонними, соответственными), широко используются в дальнейшем при изучении четырехугольников, подобных треугольников, при решении задач, а также в курсе стереометрии).
Глава 4. Соотношения между сторонами и углами треугольника (17 часов)
Сумма углов треугольника. Соотношение между сторонами и углами треугольника. Неравенство треугольника. Прямоугольные треугольники, их свойства и признаки равенства. Расстояние от точки до прямой. Расстояние между параллельными прямыми. Построение треугольника по трем элементам.
Основная цель: рассмотреть новые интересные и важные свойства треугольников. В данной теме доказывается одна из важнейших теорем геометрии — теорема о сумме углов треугольника. Она позволяет дать классификацию треугольников по углам (остроугольный, прямоугольный, тупоугольный), а также установить некоторые свойства и признаки равенства прямоугольных треугольников. Понятие расстояния между параллельными прямыми вводится на основе доказанной предварительно теоремы о том, что все точки каждой из двух параллельных прямых равноудалены от другой прямой. Это понятие играет важную роль, и частности используется в задачах на построение. При решении задач на построение в 7 классе следует ограничиться только выполнением и описанием построения искомой фигуры. В отдельных случаях можно провести устно анализ и доказательство, а элементы исследования должны присутствовать лишь тогда, когда это оговорено условием задачи.
Повторение. Решение задач. (4 часа) Повторение, обобщение и систематизация знаний, умений и навыков за курс математики 7 класс.

















