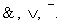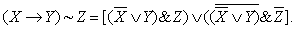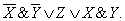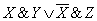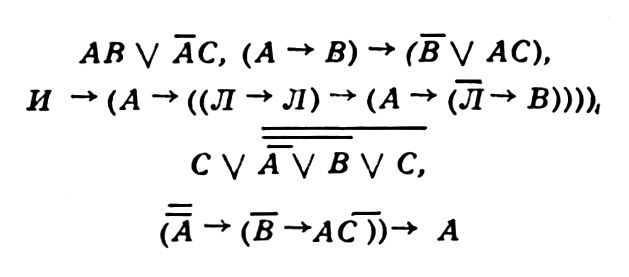Что изучает алгебра логики
Алгебра логики
Законы алгебры логики
Алгебра логики это раздел математической логики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности), и логические операции над ними.
В алгебре логики принято отождествлять истинность высказывания с числом 1, а ложность — с числом 0 (А = 1 и С = 0 означает, что А истинно и что С ложно).
Что изучает алгебра логики?
Предметом изучения алгебры логики являются функции которые принимают лишь два значения: 0 или 1. Объединение простых высказываний в сложные в алгебре логики производится без учёта внутреннего содержания (смысла) этих высказываний.
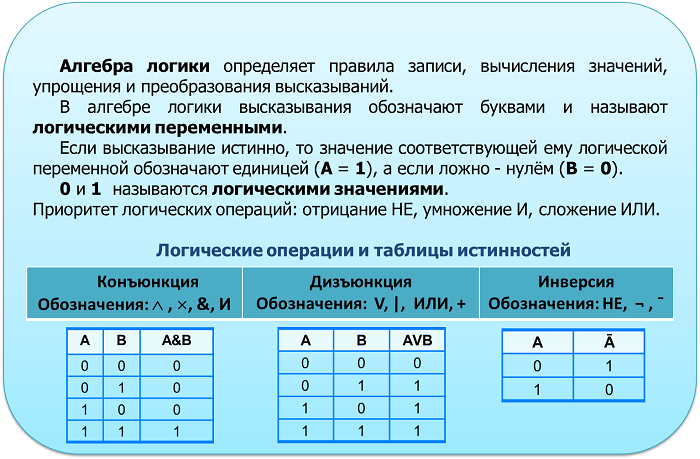
К основным логическим операциям относятся операции: отрицания, логического умножения, или конъюнкции, логического сложения, или дизъюнкции, эквивалентности, импликации.
Любое сложное выражение, полученное из простых высказываний посредством основных логических операции, называется формулой алгебры логики.
Где используется алгебра логики?
Использование аппарата алгебры логики в теории устройств дискретного действия основано на том, что элементы этих устройств являются двух позиционными приборами, т. е. приборами, которые по условиям работы могут находиться лишь в одном из двух различных устойчивых состояний, например «контакт замкнут», «транзистор открыт».
Конъюнкция такого рода высказываний будет тогда средством выражения последовательного соединения элементов, а дизъюнкция — их параллельного соединения. На этом основана возможность применять средства алгебры логики к задачам анализа и синтеза переключателей схем. Алгебра логики используется в теории релейных схем, теории ЭВМ и в теории дискретных автоматов.
Информатика не может существовать без такого важного раздела математики, который называется алгеброй логики. В данной статье будет рассказана основополагающая информация по данной теме, обозначены её главные правила и законы.
Что такое алгебра и алгебра логики
Алгебра — это раздел математики, который обобщенно можно охарактеризовать, как расширение и обобщение арифметики.
Алгебра логики — это раздел математической логики, который исследует операции над высказываниями.
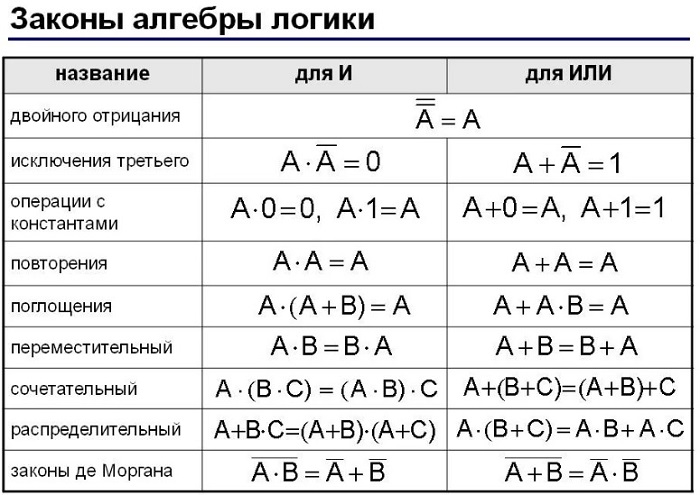
Законы алгебры логики
Имеется большое количество правил в данной сфере деятельности, но сегодня будет рассмотрено несколько основных.
Основные законы алгебры логики представлены в таблице:
Логические выражения
В информатике предоставляется два вида высказываний: простое и сложное.
Простое — это утверждение, которое обычно обозначается в виде предложения и про него можно сказать — ложное оно или истинное.
Нью-Йорк — столица США (ложное);
в России 1117 городов (верное).
Сложное высказывание обозначает некий набор простых утверждений, которые связаны логическими процессами.
Идёт дождь, а у меня нет зонта.
Основные логические операции
Логические процессы подразделяются на несколько классов. Рассмотрим их последовательно.
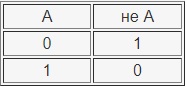
Логическое отрицание (инверсия) —НЕ
Таблица истинности инверсии:
Результаты операции НЕ следующие:
если исходное выражение истинно, то результат его отрицания будет ложным;
если исходное выражение ложно, то результат его отрицания будет истинным.
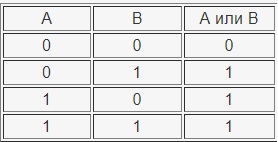
Логическое сложение (дизъюнкция, объединение) — ИЛИ
Понятие «Логическое ИЛИ» также можно заменить понятием «Дизъюнкция». Данная операция обозначается знаками — ИЛИ, OR, ||, |.
Но есть небольшое отличие: в «Логическом И» результат отрицания равен единице, если оба обозначения равны единице, а в «Логическом ИЛИ» итог равен единице, если одно из обозначений равно единице.
Таблица истинности операции ИЛИ:
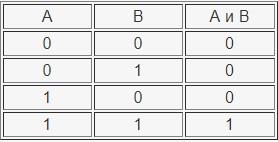
Логическое умножение(конъюнкция) — И
В истории данная операция также обозначается как логическое умножение и конъюнкция. Данная операция обозначается элементами — И, AND, &&, &.
За объект описания возьмём А и В. Оба данных выражения могут иметь или неверное значение, или правдивое значение. Для применения операции логическое умножение, и А, и В должны является истинными (то есть равными единице).
При всех остальных значениях операция будет ложной.
Таблица истинности операции И приведена ниже:
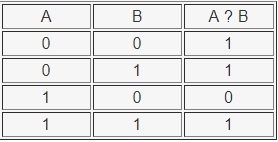
Логическое следование (импликация) — ЕСЛИ ТО
Данная программа имеет также название «Импликация». Она образуется из двух высказываний, которые соединяет: «если. то».
Необходимо запомнить, что данная операция ложна только тогда, когда из первого ложного утверждения следует ложный итог. На компьютерном языке данный процесс обозначается формулой: if. then.
Таблица истинности операции ЕСЛИ ТО выглядит так:
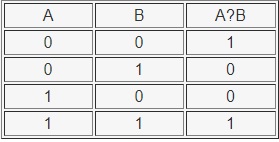
Данная операция определяется так: сложное высказывание будет истинно тогда и только тогда, когда и А, и В — истинные.
И наоборот: сложное высказывание будет ложным тогда и только тогда, когда и А, и В — ложные.
Таблица истинности операции эквивалентности:
Алгебра логики
Полезное
Смотреть что такое «Алгебра логики» в других словарях:
АЛГЕБРА ЛОГИКИ — система алгебраич. методов решения логич. задач, а также совокупность задач, решаемых такими методами. А. л. в узком смысле слова алгебраич. (табличное, матричное) построение классич. логики высказываний, в котором рассматриваются… … Философская энциклопедия
алгебра логики — АЛГЕБРА ЛОГИКИ исторически первая форма математической (символической) логики, сложившаяся к последней трети 19 в. К ее созданию привела аналогия между решением алгебраических уравнений и выводом следствий из посылок, а также то, что… … Энциклопедия эпистемологии и философии науки
алгебра логики — булева алгебра — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы булева алгебра EN logical algebra … Справочник технического переводчика
АЛГЕБРА ЛОГИКИ — система алгебраических методов решения логических задач и совокупность таких задач; в узком смысле табличное, матричное построение логики высказываний, определяющее логические операции над ними … Большой Энциклопедический словарь
АЛГЕБРА ЛОГИКИ — раздел математической логики, изучающий строение сложных логических высказываний и способы установления их истинности с помощью алгебраических методов. В формулах А. л. переменные являются логическими или двоичными, т. е. принимающими только два… … Большая политехническая энциклопедия
Алгебра логики — Не следует путать с булевой алгеброй. Алгебра логики (алгебра высказываний) раздел математической логики, в котором изучаются логические операции над высказываниями[1]. Чаще всего предполагается (т. н. бинарная или двоичная логика, в… … Википедия
алгебра логики — система алгебраических методов решения логических задач и совокупность таких задач. * * * АЛГЕБРА ЛОГИКИ АЛГЕБРА ЛОГИКИ, система алгебраических методов решения логических задач и совокупность таких задач; в узком смысле табличное, матричное… … Энциклопедический словарь
алгебра логики — logikos algebra statusas T sritis automatika atitikmenys: angl. algebra of logic vok. Algebra der Logik, f; logische Algebra, f rus. алгебра логики, f pranc. algèbre logique, f … Automatikos terminų žodynas
АЛГЕБРА ЛОГИКИ — раздел математической логики, изучающий высказывания, рассматриваемые со стороны их логич. значений (истинности пли ложности), и логич. операций над ними. А. л. возникла в сер. 19 в. в трудах Дж. Буля (см. [1], [2]) и развилась затем в работах Ч … Математическая энциклопедия
АЛГЕБРА ЛОГИКИ — раздел матем. логики, изучающий высказывания, рассматриваемые со стороны их логич. значений (истинности или ложности), и логич. операции над ними. В А. л. принято отождествлять истинность высказывания с числом 1, а ложность с числом О (А = 1 и С … Большой энциклопедический политехнический словарь
Алгебра логики
Из Википедии — свободной энциклопедии
Основоположником её является Дж. Буль, английский математик и логик, положивший в основу своего логического учения аналогию между алгеброй и логикой. Алгебра логики стала первой системой математической логики, в которой алгебраическая символика стала применяться к логическим выводам в операциях с понятиями, рассматриваемыми со стороны их объёмов. Буль ставил перед собой задачу решить логические задачи с помощью методов, применяемых в алгебре. Любое суждение он пытался выразить в виде уравнений с символами, в которых действуют логические законы, подобные законам алгебры.
Впоследствии усовершенствованием алгебры логики занимались У. С. Джевонс, Э. Шрёдер, П. С. Порецкий, Ч. Пирс, Г. Фреге, разработавший теорию исчисления высказываний, Д. Гильберт, добившийся успехов в области применения метода формализации в операциях с логическими высказываниями. Внесли свой вклад Б. Рассел, придавший вместе с А. Уайтхедом, математической логике современный вид; И. И. Жегалкин, заслугой которого явилась дальнейшая разработка исчисления классов и значительное упрощение теории операций логического сложения; В. И. Гливенко вынес предмет алгебры логики далеко за рамки изучения объёмных операций с понятиями.
Алгебра логики в её современном изложении занимается исследованием операций с высказываниями, то есть с предложениями, которые характеризуются только одним качеством — истинностным значением (истина, ложь). В классической алгебре логики высказывание одновременно может иметь только одно из двух истинностных значений: «истина» или «ложь». Алгебра логики исследует также высказывания — функции, которые могут принимать значения «истина» и «ложь» в зависимости от того, какое значение будет придано переменной, входящей в высказывание — функцию.
АЛГЕБРА ЛОГИКИ
Полезное
Смотреть что такое «АЛГЕБРА ЛОГИКИ» в других словарях:
алгебра логики — АЛГЕБРА ЛОГИКИ исторически первая форма математической (символической) логики, сложившаяся к последней трети 19 в. К ее созданию привела аналогия между решением алгебраических уравнений и выводом следствий из посылок, а также то, что… … Энциклопедия эпистемологии и философии науки
алгебра логики — булева алгебра — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы булева алгебра EN logical algebra … Справочник технического переводчика
АЛГЕБРА ЛОГИКИ — система алгебраических методов решения логических задач и совокупность таких задач; в узком смысле табличное, матричное построение логики высказываний, определяющее логические операции над ними … Большой Энциклопедический словарь
АЛГЕБРА ЛОГИКИ — раздел математической логики, изучающий строение сложных логических высказываний и способы установления их истинности с помощью алгебраических методов. В формулах А. л. переменные являются логическими или двоичными, т. е. принимающими только два… … Большая политехническая энциклопедия
Алгебра логики — раздел математической логики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности), и логические операции над ними. А. л. возникла в середине 19 в. в трудах Дж. Буля (См. Буль) и развивалась… … Большая советская энциклопедия
Алгебра логики — Не следует путать с булевой алгеброй. Алгебра логики (алгебра высказываний) раздел математической логики, в котором изучаются логические операции над высказываниями[1]. Чаще всего предполагается (т. н. бинарная или двоичная логика, в… … Википедия
алгебра логики — система алгебраических методов решения логических задач и совокупность таких задач. * * * АЛГЕБРА ЛОГИКИ АЛГЕБРА ЛОГИКИ, система алгебраических методов решения логических задач и совокупность таких задач; в узком смысле табличное, матричное… … Энциклопедический словарь
алгебра логики — logikos algebra statusas T sritis automatika atitikmenys: angl. algebra of logic vok. Algebra der Logik, f; logische Algebra, f rus. алгебра логики, f pranc. algèbre logique, f … Automatikos terminų žodynas
АЛГЕБРА ЛОГИКИ — раздел математической логики, изучающий высказывания, рассматриваемые со стороны их логич. значений (истинности пли ложности), и логич. операций над ними. А. л. возникла в сер. 19 в. в трудах Дж. Буля (см. [1], [2]) и развилась затем в работах Ч … Математическая энциклопедия
АЛГЕБРА ЛОГИКИ — раздел матем. логики, изучающий высказывания, рассматриваемые со стороны их логич. значений (истинности или ложности), и логич. операции над ними. В А. л. принято отождествлять истинность высказывания с числом 1, а ложность с числом О (А = 1 и С … Большой энциклопедический политехнический словарь