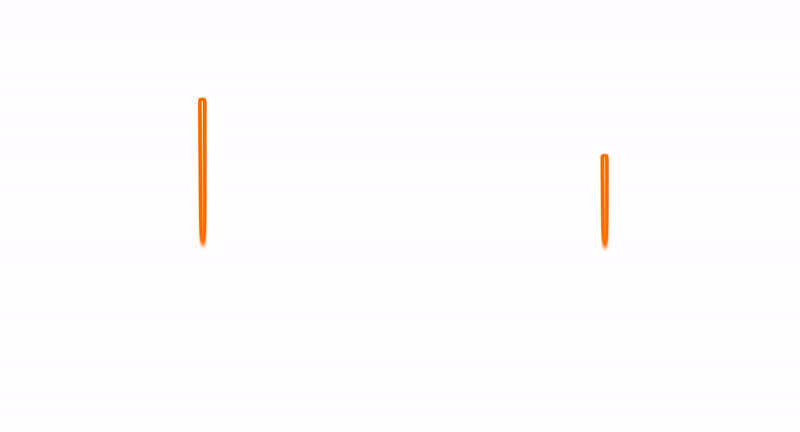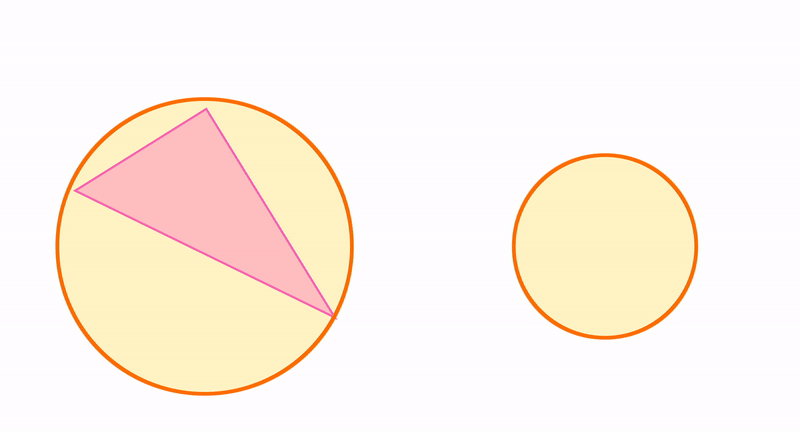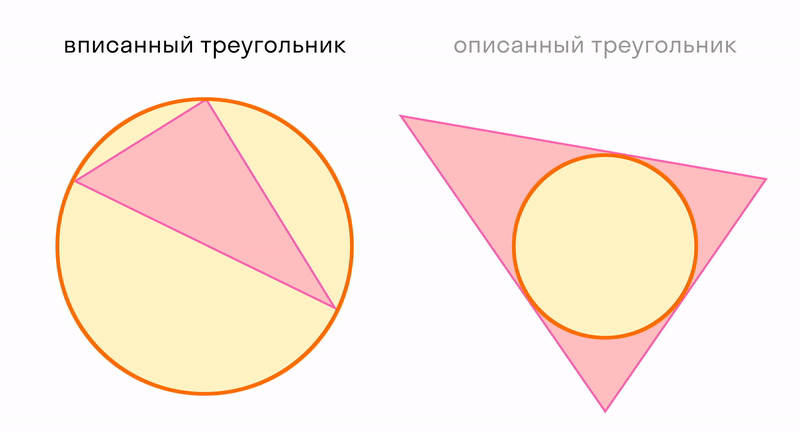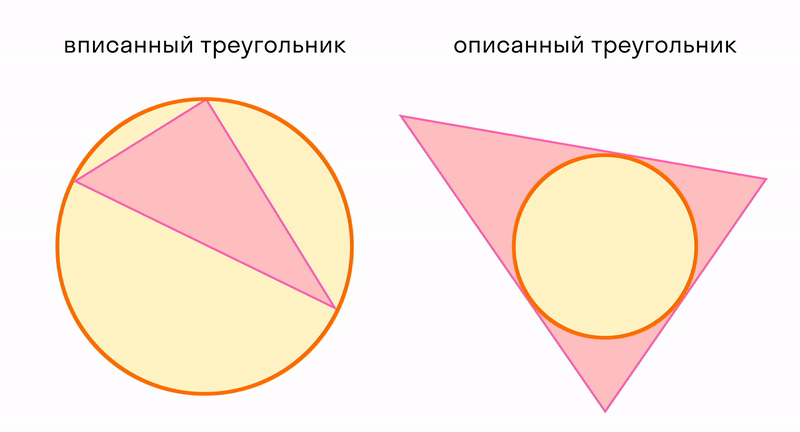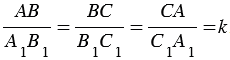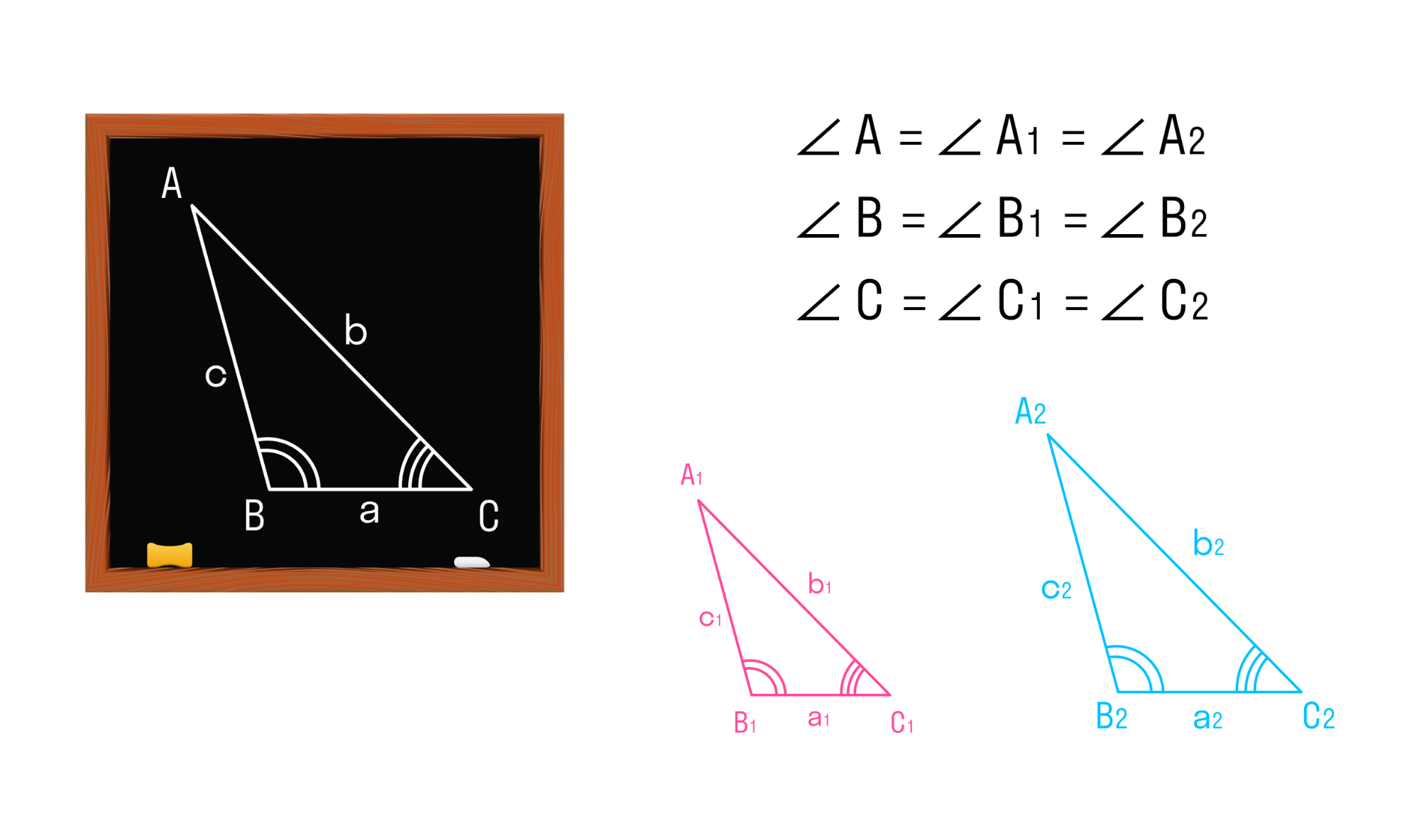Что изучает алгебра и геометрия

Разделы математики

Существует три официальных способа подразделения математики.

Содержание

Математика как специальность

Математика как специальность научных работников министерства науки и технологий Российской Федерации [1] подразделяется на научные специальности

Математика как учебная дисциплина

Математика как учебная дисциплина подразделяется в Российской Федерации на элементарную математику, изучаемую в средней школе, и образованную дисциплинами:

и высшую математику, изучаемую в ВУЗе. Дисциплины, входящие в состав высшей математики, варьируются в зависимости от специальности. Программа обучения по специальности математика [2] образована следующими учебными дисциплинами:

Знаком (ф) отмечены дисциплины, которые изучаются при обучении по специальности «физика».

Систематизация научных работ

Для систематизации научных работ используется Универсальная десятичная классификация 51.

Примечания

Полезное

Смотреть что такое «Разделы математики» в других словарях:

МАТЕМАТИКИ ИСТОРИЯ — Самой древней математической деятельностью был счет. Счет был необходим, чтобы следить за поголовьем скота и вести торговлю. Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела, главным образом… … Энциклопедия Кольера

История математики — История науки … Википедия

История математики в России — Данная статья часть обзора История математики. Содержание 1 Древность и средневековье 2 XVII век 3 … Википедия

Философия математики — учение о сущности математического знания и о базовых принципах математических доказательств, раздел философии науки; её можно также назвать «метаматематикой». Содержание 1 Возможность оснований математики 2 Литература … Википедия

История математики в Индии — Данная статья часть обзора История математики. Научные достижения индийской математики широки и многообразны. Уже в древние времена учёные Индии на своём, во многом оригинальном пути развития достигли высокого уровня математических знаний.… … Википедия

Институт математики и механики (НИИММ СПбГУ) — Научно исследовательский институт математики и механики имени академика В. И. Смирнова (НИИММ СПбГУ) структурное подразделение Санкт Петербургского государственного университета. Выполняет организационную роль, является материальной базой для… … Википедия

Математика — Евклид. Деталь «Афинской школы» Рафаэля Математика (от др. греч … Википедия

Дискретная математика — Дискретная математика область математики, занимающаяся изучением дискретных структур, которые возникают как в пределах самой математики, так и в её приложениях. К числу таких структур могут быть отнесены конечные группы, конечные графы, а… … Википедия

Математический анализ — У этого термина существуют и другие значения, см. Анализ. Математический анализ совокупность разделов математики, посвящённых исследованию функций и их обобщений методами дифференциального и интегрального исчислений. При столь общей… … Википедия

МЕТОД АКСИОМАТИЧЕСКИЙ — способ построения теории, при к ром в ее основу кладутся нек рые ее положения – аксиомы или постулаты, – из к рых все остальные положения теории (теоремы) выводятся путем рассуждений, называемых д о к а з а т е л ь с т в а м и. Правила, по к рым… … Философская энциклопедия

Источник

Алгебра

А́лгебра (от араб. الجبر ‎‎, «аль-джабр» — восполнение [1] ) — раздел математики, который можно грубо охарактеризовать как обобщение и расширение арифметики. Слово «алгебра» также употребляется в названиях различных алгебраических систем. В более широком смысле под алгеброй понимают раздел математики, посвящённый изучению операций над элементами множества произвольной природы, обобщающий обычные операции сложения и умножения чисел.

Алгебра — это наука, изучающая алгебраические системы с точностью до изоморфизма.

Алгебраическая система — упорядоченная пара множеств . Первое множество () — элементы какой либо природы (числа, понятия, буквы). Второе множество () — операции над первым множеством (сложение, умножение, возведение в степень). Примеры: группа, кольцо, поле.

Содержание

История

Истоки алгебры уходят к временам глубокой древности. Ещё 4000 лет назад вавилонские учёные могли решать квадратные уравнения. Тогда никаких обозначений не было, и уравнения записывались в словесной форме. Первые обозначения появились в Древней Греции благодаря учёному Диофанту. Неизвестное число он назвал «ἀριθμός», вторую степень неизвестного — «δύναμις», третью «κύβος», четвёртую — «дюнамодюнамис», пятую — «дюнамокюбос», шестую — «кюбоккюбос». Все эти величины он обозначал сокращениями (ар, дю, кю, ддю, дкю, ккю). Ни вавилоняне, ни греки не знали и не признавали отрицательные числа.

За 2000 лет до нашего времени китайские учёные решали уравнения первой степени и их системы, а также квадратные уравнения. Они уже знали отрицательные и иррациональные числа. Поскольку в китайском языке каждый символ обозначает понятие, то сокращений не было. В 13 веке китайцы открыли закон образования биномиальных коэффициентов, ныне известный как «треугольник Паскаля». В Европе он был открыт лишь 250 лет спустя. [2]

В 12 веке алгебра попала в Европу. С этого времени начинается её бурное развитие. Были открыты способы решения уравнений 3 и 4 степеней. Распространения получили отрицательные и комплексные числа. Было доказано, что любое уравнение выше 4 степени нельзя решить алгебраическим способом.

Вплоть до второй половины XX века практическое применение алгебры ограничивалось, в основном, решением алгебраических уравнений и систем уравнений с несколькими переменными. Во второй половине XX века началось бурное развитие ряда новых отраслей техники. Появились электронно-вычислительные машины, устройства для хранения, переработки и передачи информации, системы наблюдения типа радара. Проектирование новых видов техники и их использование немыслимо без применения современной алгебры. Так, электронно-вычислительные машины устроены по принципу конечных автоматов. Для проектирования электронно-вычислительных машин и электронных схем используются методы булевой алгебры. Современные языки программирования для ЭВМ основаны на принципах теории алгоритмов. Теория множеств используется в системах компьютерного поиска и хранения информации. Теория категорий используется в задачах распознавания образов, определении семантики языков программирования, и других практических задачах. Кодирование и декодирование информации производится методами теории групп. Теория рекуррентных последовательностей используется в работе радаров. Экономические расчеты невозможны без использования теории графов. Математическое моделирование широко использует все разделы алгебры.

Классификация

Алгебру можно грубо разделить на следующие категории:

В некоторых напралениях углублённого изучения, аксиоматические алгебраические системы, такие как группы, кольца, поля и алгебры над полем на присутствие геометрических структур (метрик и топологий), совместимых с алгебраическими структурами. Список некоторых разделов функционального анализа:

Элементарная алгебра

Элементарная алгебра — раздел алгебры, который изучает самые базовые понятия. Обычно изучается после изучения основных понятий арифметики. В арифметике изучаются числа и простейшие (+, −, ×, ÷) действия с ними. В алгебре числа заменяются на переменные (a,b,c,x,y и так далее). Такой подход полезен, потому что:

Источник

Вот зачем нужна школьная алгебра

Обычно на вопрос «зачем нужна математика?» отвечают что-то вроде «гимнастика для ума». На мой взгляд, этого объяснения недостаточно. Когда человек выполняет физические упражнения, то он знает точное название групп мышц, которые при этом развиваются. Но разговоры про математику остаются слишком абстрактными. Какие конкретно «мышцы ума» тренируются школьной алгеброй? Она ведь совсем не похожа на настоящую математику, в которой делаются великие открытия. Что дает умение искать производную каких-то запутанных функций?

Преподавание программирования слабым студентам привело меня к более точному ответу на вопрос «зачем?». В статье я постараюсь донести его вам.

В данном примере от ученика ожидают, что он вспомнит формулу квадрата суммы

В более сложных случаях, полученное выражение можно использовать для других преобразований. Например:

преобразуется сначала в

Чтобы добиться такого результата, ученику нужно распознать в исходном выражении и потом применить три формулы:

Это практически определение рефакторинга из одноименной книги Мартина Фаулера.

В своем труде, автор формулирует их следующим образом:

Рефакторинг (Refactoring) (сущ.): изменение во внутренней структуре программного обеспечения, имеющее целью облегчить понимание его работы и упростить модификацию, не затрагивая наблюдаемого поведения.

Производить рефакторинг (Refactor) (глаг.): изменять структуру программного обеспечения, применяя ряд рефакторингов, не затрагивая его поведения.

В книге даются «формулы», которые нужно распознать в исходном коде и правила их преобразования.

В качестве простейшего примера, приведу «введение поясняющей переменной» из книги:

Части выражения нужно записать в переменную, имя которой поясняет его назначение.

Представьте себе человека, который не может упрощать алгебраические выражения с использованием формулы квадрата суммы и разности квадратов.

Как вы думаете, сможет ли этот человек рефакторить код?

Сможет ли он вообще написать понятный другим людям код, если у него не сформирован идеал этой самой лаконичности? На мой взгляд — нет.

Однако в школе учатся все, а программистами становится меньшинство. Полезен ли навык преобразования выражений для обычных людей? Я думаю да. Только навык применяется в более абстрактном виде: нужно оценить ситуацию и выбрать дальнейшее действие так, чтобы приблизиться к цели. В педагогике этот феномен называется перенос (навыка).

Даже при езде на автомобильном транспорте, водитель постоянно занимается распознаванием шаблонов в окружающем мире и выполнением соответствующих маневров, чтобы добраться до цели.

Когда ты умер, ты об этом не знаешь, только другим тяжело. То же самое, когда ты не освоил математику…

Что же происходит, если человеку не удалось освоить преобразование выражений? Время от времени я веду индивидуальные занятия со студентами, у которых в школе было плохо с математикой. Как правило, они напрочь застревают на теме про циклы. Настолько, что с ними приходится заниматься «алгеброй», но на языке программирования.
Это происходит потому, что при написании циклов основной прием как раз и заключается в том, чтобы преобразовать группу одинаковых выражений.

Допустим результат работы программы должен выглядеть так:

Введение
Глава 1
Глава 2
Глава 3
Глава 4
Глава 5
Глава 6
Глава 7
Заключение

Тривиальная программа для достижения этого результата выглядит так:

Но это решение далеко от лаконичного идеала. Сначала в нем нужно найти повторяющуюся группу действий и потом преобразовать. В итоге получится такое решение:

Если же человек в свое время не освоил математику, то и выполнять подобные преобразования он не сможет. У него просто не будет соответствующего навыка. Именно поэтому тема циклов — первое препятствие в обучении разработчика.

Похожие проблемы возникают и в других областях. Если человек не умеет использовать подручный инструмент, то он не сможет проявлять бытовую смекалку. Злые языки будут говорить, что руки не из того места растут. На дороге это проявляется в неумении правильно оценить ситуацию и выбрать маневр. Что иногда может привести к трагическим последствиям.

Источник

Как появилась алгебра и геометрия

в данной презентация история появления алгебры и геометрии.

Просмотр содержимого документа
«Как появилась алгебра и геометрия»

КАК ПОЯВИЛАСЬ АЛГЕБРА И ГЕОМЕТРИЯ

Алгебра, вместе с арифметикой, есть наука о числах и через посредство чисел – о величинах вообще. Не занимаясь изучением свойств каких-нибудь определенных, конкретных величин, обе эти науки исследуют свойства отвлеченных величин, как таковых, независимо от того, к каким конкретным приложениям они способны. Различие между арифметикой и алгеброй состоит в том, что первая наука исследует свойства данных, определенных величин, между тем как алгебра занимается изучением общих величин, значение которых может быть произвольное, а, следовательно, алгебра изучает только те свойства величин, которые общи всем величинам, независимо от их значений. Таким образом, алгебра есть обобщенная арифметика. Это подало повод Ньютону назвать свой трактат об алгебре «Общая арифметика». Гамильтон, полагая, что подобно тому, как геометрия изучает свойства пространства, алгебра изучает свойства времени, назвал алгебру «Наукою чистого времени» – название, которое Морган предлагал изменить на «Исчисление последовательности». Однако такие определения не выражают ни существенных свойств алгебры, ни исторического ее развития. Алгебру можно определить как «науку о количественных соотношениях».

раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Геометрия как систематическая наука появилась в Древней Греции, её аксиоматические построения описаны в «Началах» Евклида. Евклидова геометрия занималась изучением простейших фигур на плоскости и в пространстве, вычислением их площади и объёма. Предложенный Декартом в 1637 году координатный метод лёг в основу аналитической и дифференциальной геометрии, а задачи, связанные с черчением, привели к созданию начертательной и проективной геометрии. При этом все построения оставались в рамках аксиоматического подхода Евклида. Коренные изменения связаны с работами Лобачевского в 1829 году, который отказался от аксиомы параллельности и создал новую неевклидову геометрию, определив таким образом путь дальнейшего развития науки и создания новых теорий.

Арифметика изучается с самых древних сохранившихся текстов, относимых к математике. В нынешних справочниках признается, что на развитие алгебры оказал влияние труд древнегреческого математика Диофанта Александрийского «Арифметика» (3 век с рождества Христова).

В труде арабского математика Мухаммеда аль-Хорезми под названием «Альджебр аль-мукабала» (9 век нашей эры), рассмотрены методы решения задач, сводящихся в современной терминологии к алгебраическим уравнениям первой и второй степеней. От названия этой работы и произошел термин «алгебра».

В 15-17 веках в работах европейских математиков появились применяемые в настоящее время обозначения алгебраических операций («+», «-»), скобки, знаки радикалов, обозначение степеней числа. Франсуа Виет в конце 16 века ввел буквенные обозначения для переменных.

В 17-18 веках под алгеброй понимается наука о вычислениях с использованием переменных, записанных с помощью букв, в частности решение алгебраических уравнений. В настоящее время в школьном образовании подобные буквенные вычисления называются элементарной алгеброй.

с помощью элементарных арифметических операций и операции извлечения корней становится центральной задачей алгебры.

Итальянскими математиками в 15 веке были найдены формулы для решения общего уравнения 3-й и 4-й степени, однако для более высоких степеней задача до 19 века не поддавалась решению.

В 1824 году норвежский математик Нильс Абель доказал, что уравнения выше 4-й степени в общем случае в радикалах не разрешимы. В 1830 году французский математик Эварист Галуа в рамках созданной им теории Галуа вывел общий критерий разрешимости алгебраического уравнения в радикалах.

С середины 19 века в центре алгебраических исследований оказывается изучение произвольных алгебраических операций. Так расширялось понятия числа, появилось понятие алгебра логики, были исследованы кватернионы, создано матричное исчисление, получила развитие теория групп.

Алгебра как общая теория произвольных алгебраических операций стала восприниматься с начала 20 века с появлением работ Давида Гильберта, Э. Штейница, Э. Артина, Эмми Нётер. Это понимание было закреплено в вышедшей в 1930 году монографии Б. Л. ван дер Вардена «Современная алгебра», остающейся до настоящего времени востребованным учебником по алгебре.

Источник

Основы геометрии

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Идеальные объекты

Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.

Основные геометрические объекты: окружность, квадрат, ромб, прямоугольник, равносторонний треугольник, равнобедренный треугольник, правильный многоугольник, эллипс и другие.

Все эти фигуры обладают двумя свойствами:

Равенство частей можно заметить у квадрата, ромба или равностороннего треугольника — равенство сторон. Также у них есть одна или несколько линий симметрии.

У шара бесконечное количество осей симметрии и плоскостей симметрии, но отсутствует равенство или подобие составных частей.

Все типы правильных многогранников обладают симметрией, при этом составлены из некоторого количества одинаковых фигур (треугольников, квадратов, пятиугольников).

Из всего этого можно сделать вывод, что отличить правильную геометрическую фигуру от произвольной совсем не сложно. Достаточно выяснить, имеет ли данная фигура оси или плоскости симметрии, а также из каких повторяющихся частей она состоит.

Таким образом, именно по наличию или отсутствию симметрии и равенства или подобия составных частей можно оценивать различные объекты окружающего мира на соответствие правильному геометрическому виду.

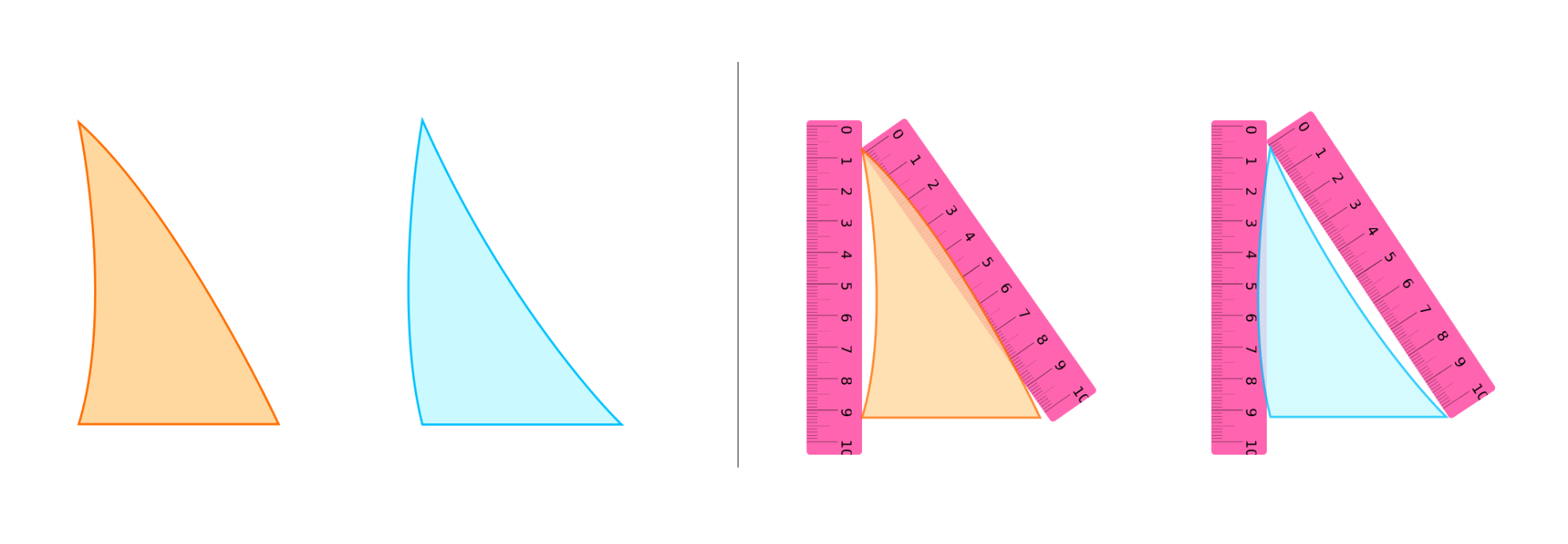
Например, возьмем два треугольника. На первый взгляд, они похожи, но у одного из них одна сторона вогнутая, вторая — выпуклая. А у другого наоборот.

Математика занимается идеальными объектами и делает о них некие заключения, которые называют теоремами. Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.

Например, теорема Пифагора звучит так: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. А затем это свойство можно применять при решении задач и составлении чертежей.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Базовые геометрические объекты

Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.

Точка — это идеальный математический объект, у которого нет длины и ширины.

Отрезок — это часть прямой, у которого есть начало и конец.

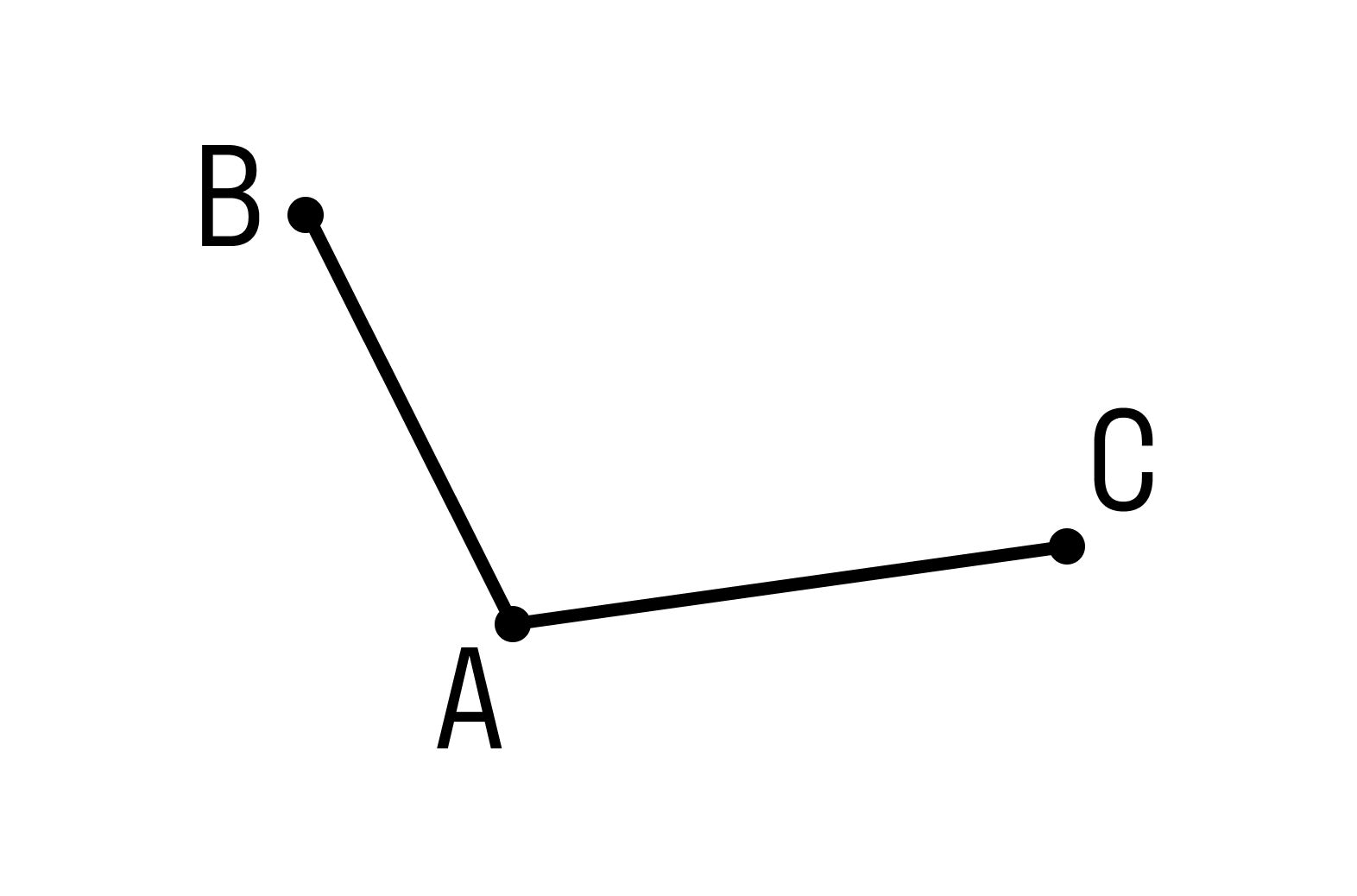
Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.

Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.

Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.

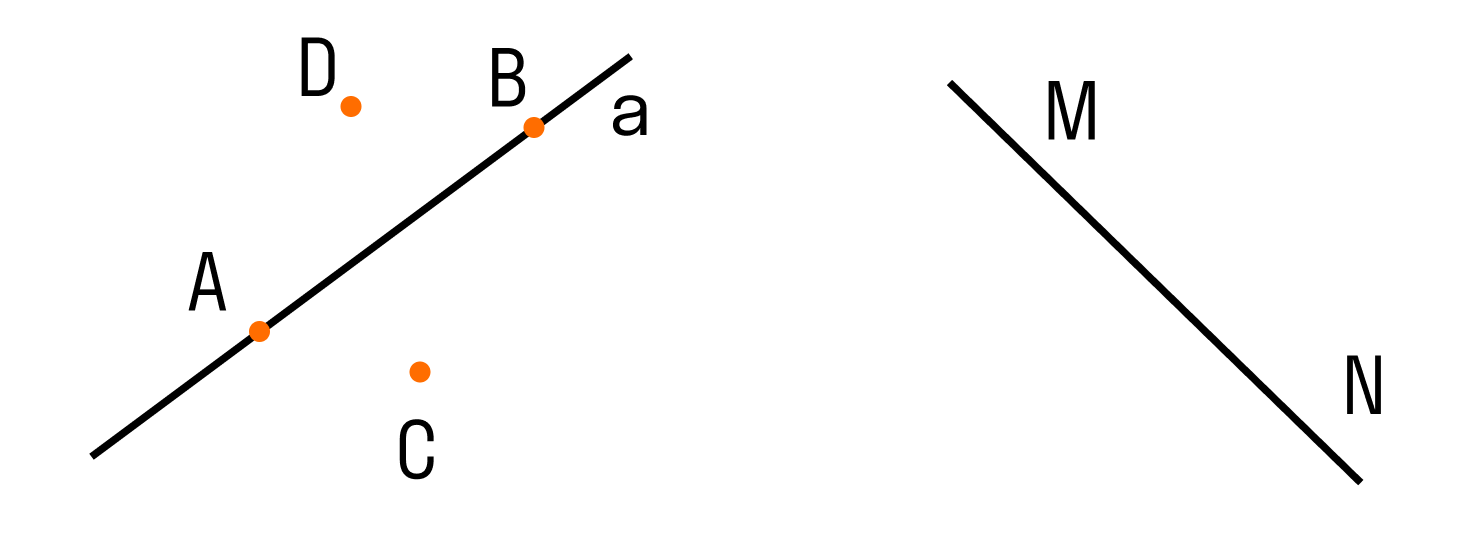
Обозначать прямые принято малыми латинскими буквами (a, b,c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).

Два варианта расположения точек относительно прямой:

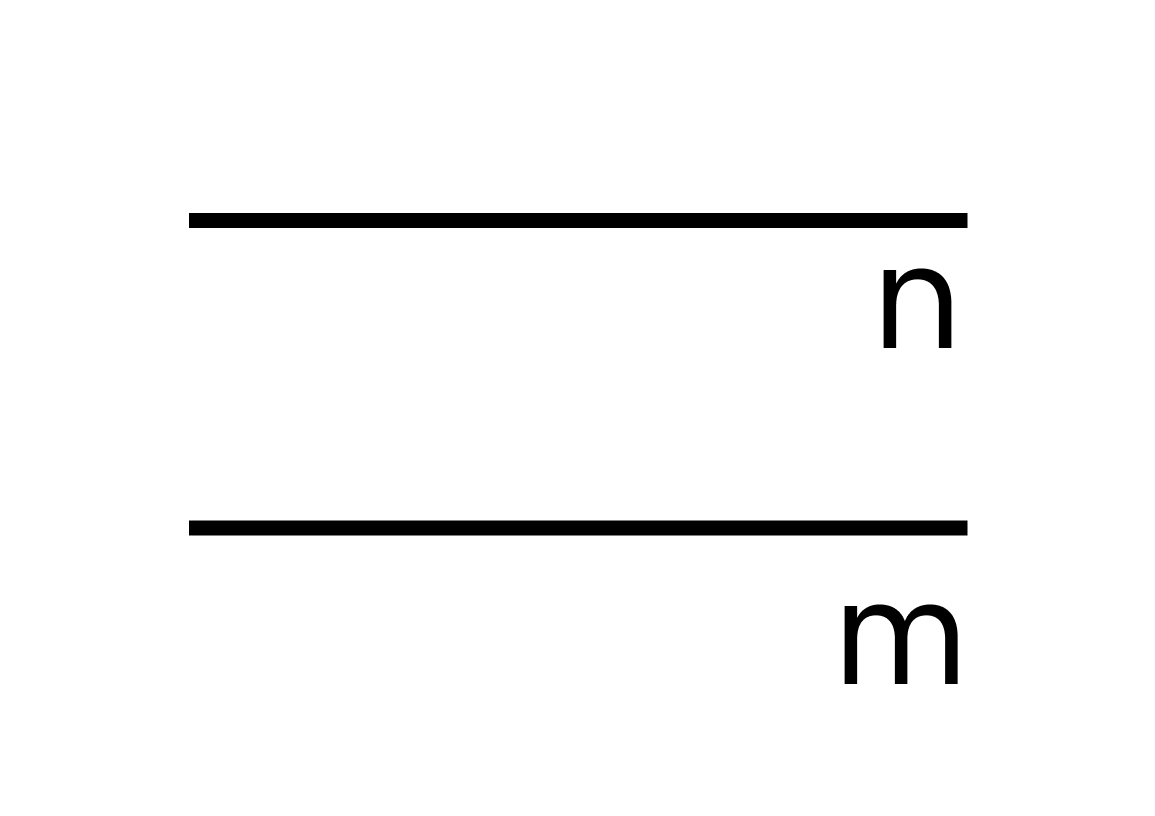
Если рассмотреть две прямые, то возможны два варианта их расположения:

Для записи не пересекающихся прямых используют специальный знак — ,
то есть m n (читают: прямая m не пересекает прямую n).

Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.

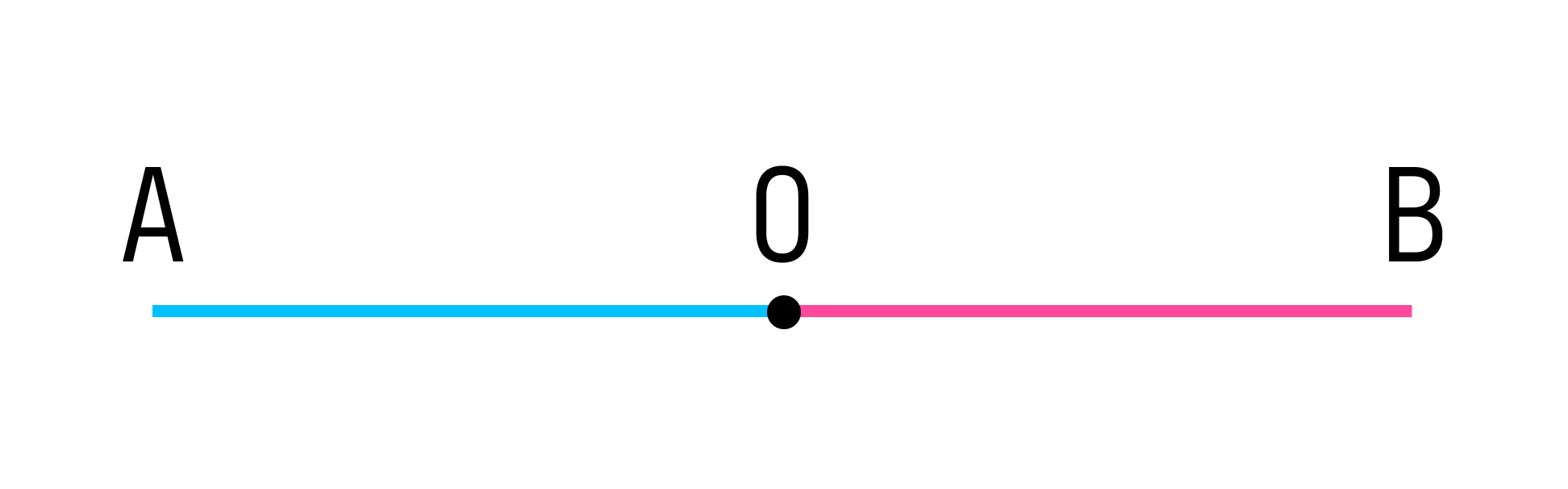
На рисунке точка О разбивает прямую АВ на две части:

Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.

Назовем получившиеся лучи:

Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.

Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости

Комбинации простейших объектов

Поговорим про комбинации простейших объектов. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).

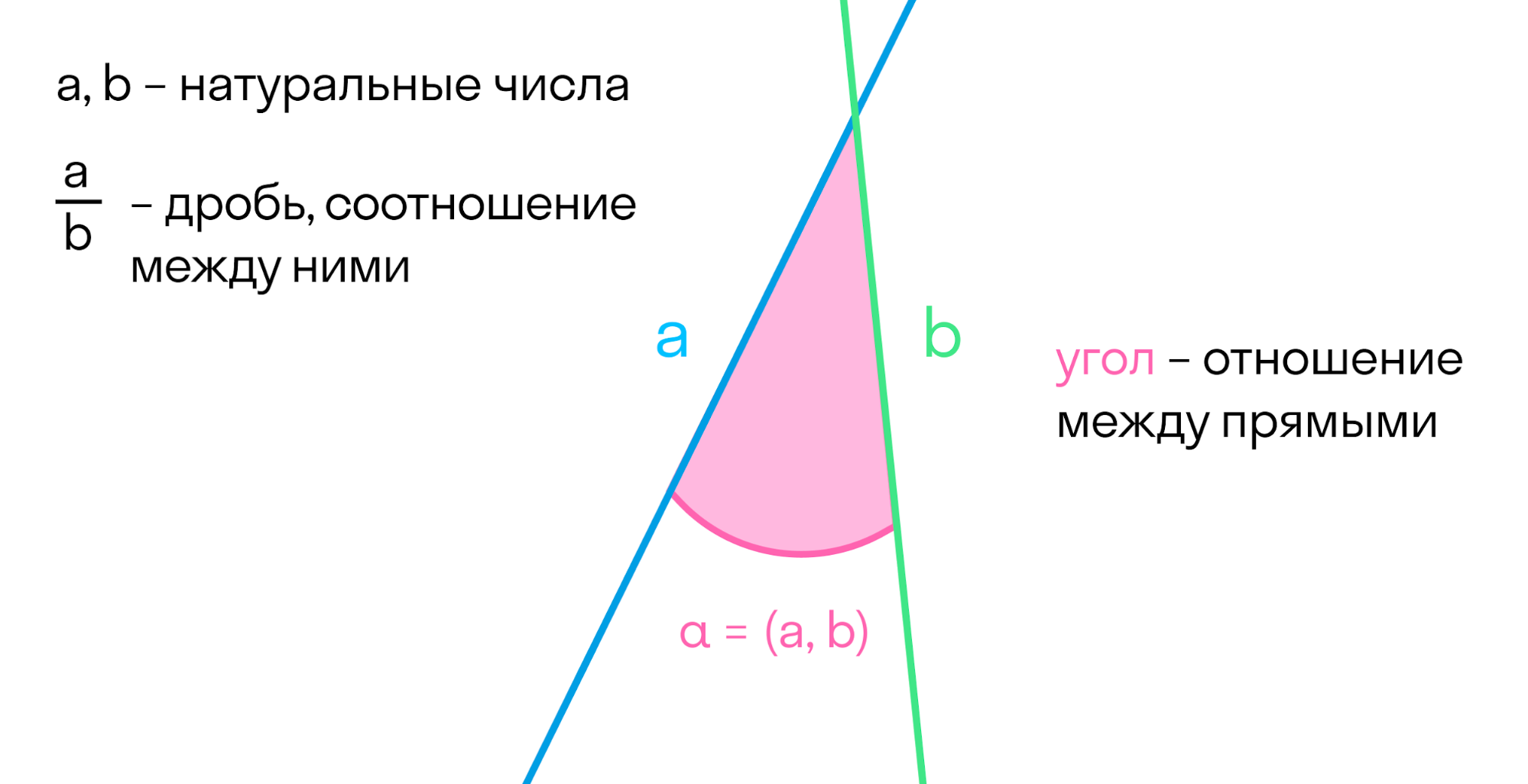
Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Аналогично мы поступали с числами: ввели натуральные числа — количество предметов в множестве. А после этого изучали отношения между этими числами: дроби, возведение в степень.

Точно так же мы изучали множества, а после — отношения между множествами, функции.

Две прямые образуют углы. По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.

Максимальный угол – это полный оборот, он составляет 360 градусов.

Угол — это часть плоскости, ограниченная двумя лучами, которые выходят из одной точки. Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.

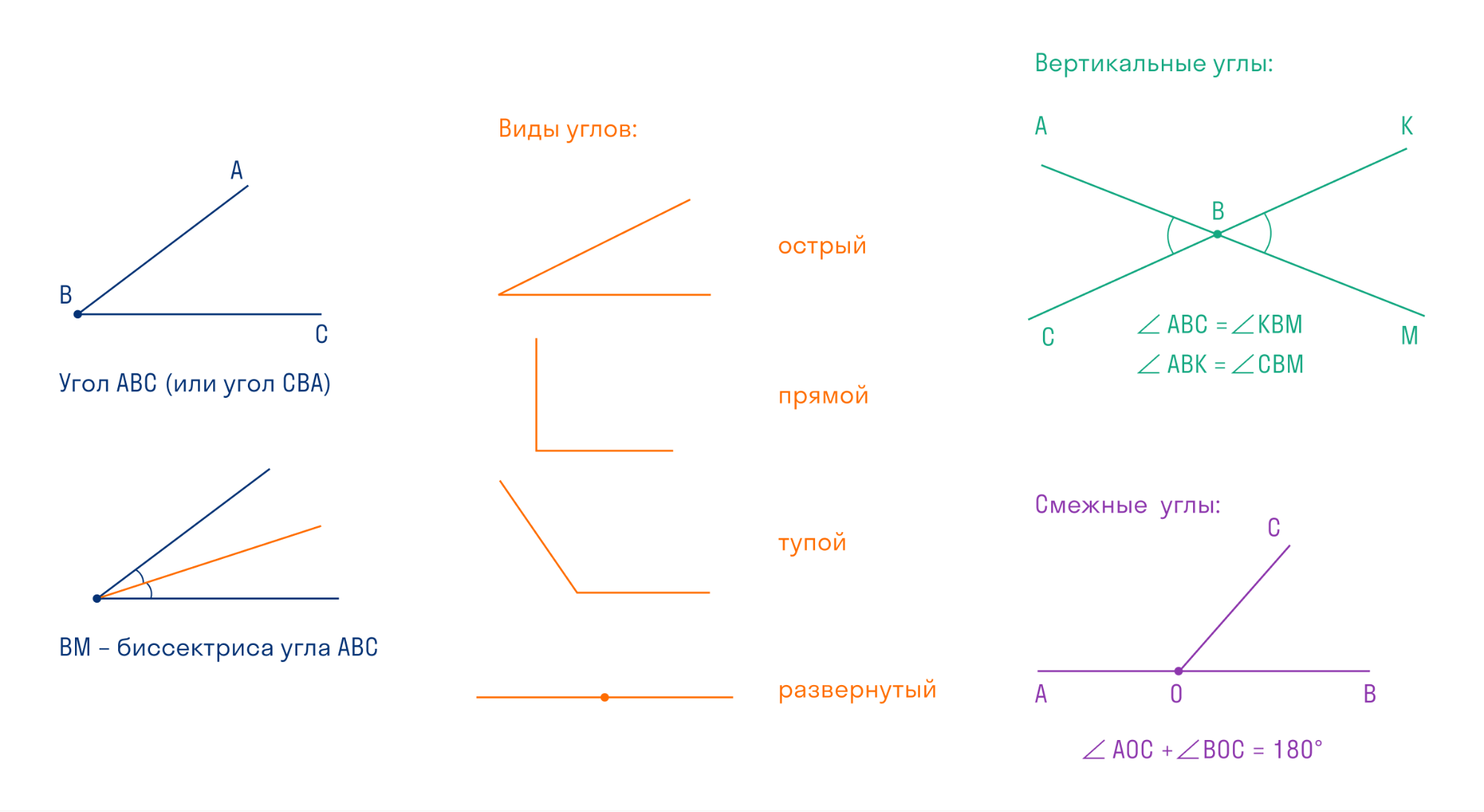
Есть разные виды углов, выделим самые часто встречающиеся:

Точка называется вершиной угла, а лучи — сторонами угла.

Два угла называются вертикальными, если их стороны являются дополнительными лучами. Свойство вертикальных углов звучит так: вертикальные углы равны.

Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами. Свойство смежных углов: сумма смежных углов равна 180°.

Биссектриса угла — это луч с началом в вершине угла, который делит угол на две равные части.

А теперь посмотрим на взаимное расположение трех прямых.

Первый случай: все три прямые параллельны.

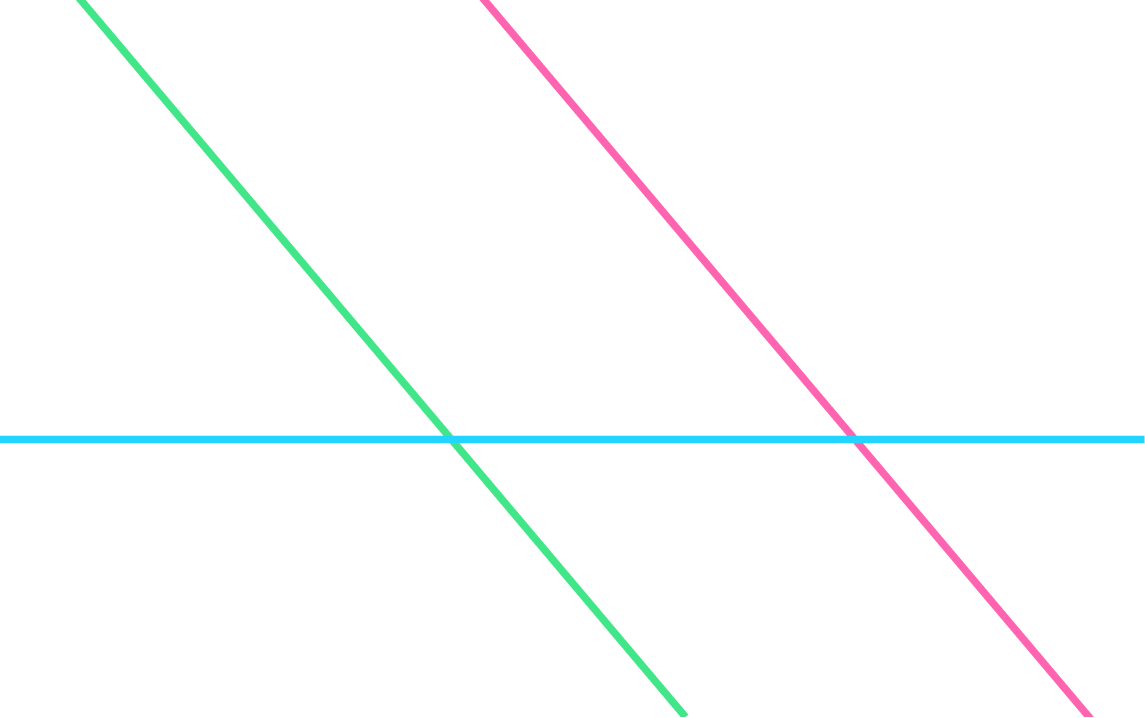
Второй случай: две прямые параллельны, а третья их пересекает.

Третий случай: если провести три прямые на плоскости случайным образом, велика вероятность образования треугольника. Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.

Треугольник

Треугольник образуют три прямые. Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.

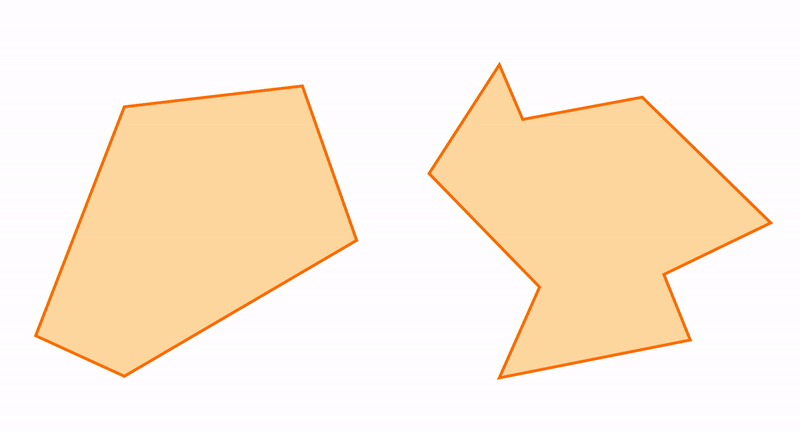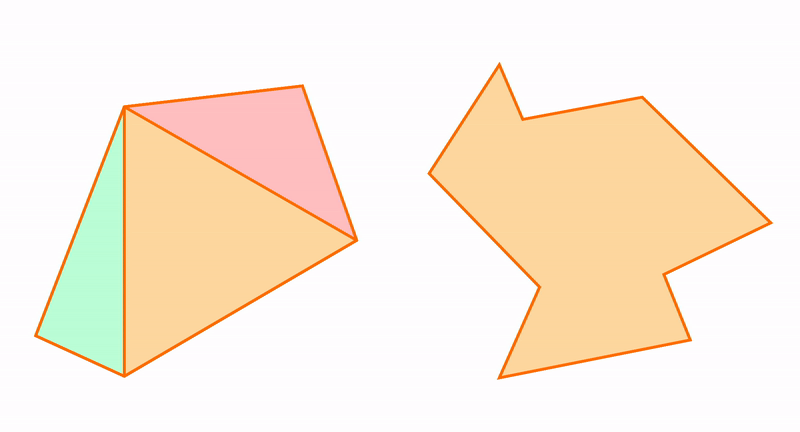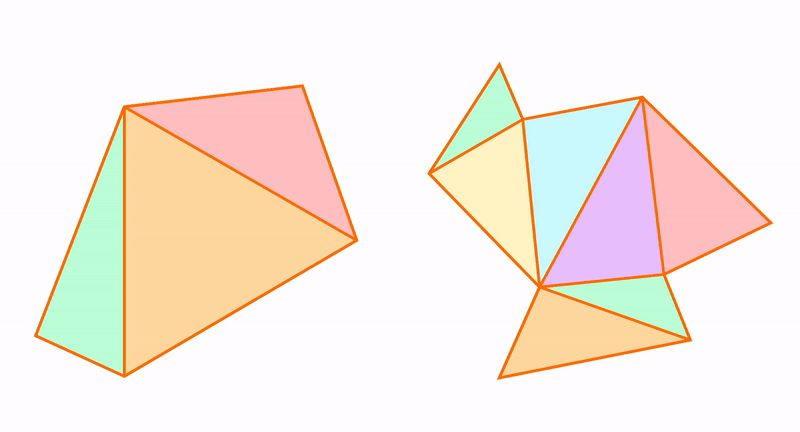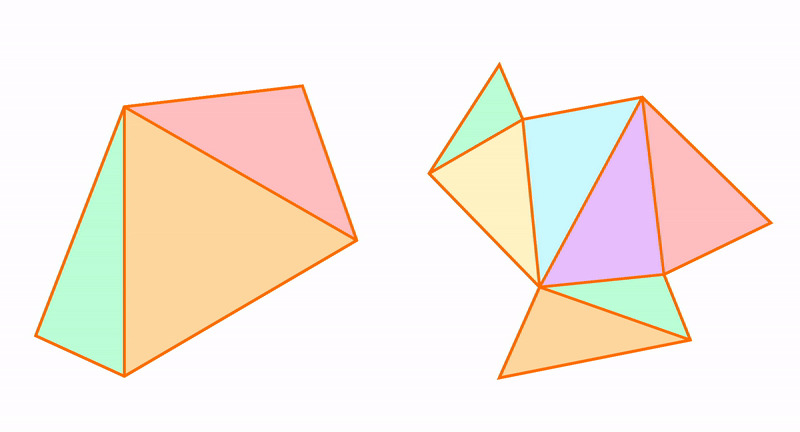
Из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников.

Треугольник можно использовать для измерения расстояний. А еще треугольник можно рассматривать в отношениях с окружностью, которая тоже является элементарной конструкцией. Читайте про вписанные и описанные углы.

Треугольник можно легко вычислить, то есть найти его площадь по трем элементам:

Приходи на наши онлайн уроки по математике с лучшими препадавателями! Для учеников с 1 по 11 классы!

Свойства треугольников

Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.

Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника.

Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.

Сумма любых двух сторон треугольника больше его третьей стороны.

Еще одно свойство верное для всех треугольников: сумма всех углов треугольника составляет половину полного оборота. Или по-другому: сумма углов треугольника — два прямых угла.

Мы знаем, что две геометрические фигуры считают равными, если их можно совместить наложением. Это справедливо и для треугольников. Равные фигуры имеют равные размеры и формы. Значит, если два треугольника равны — элементы одного треугольника соответственно равны элементам другого треугольника.

Равенство треугольников ABC и A₁B₁C₁ обозначается так: ΔABC = ΔA₁B₁C₁.

Есть даже специальные теоремы про равенство треугольников.

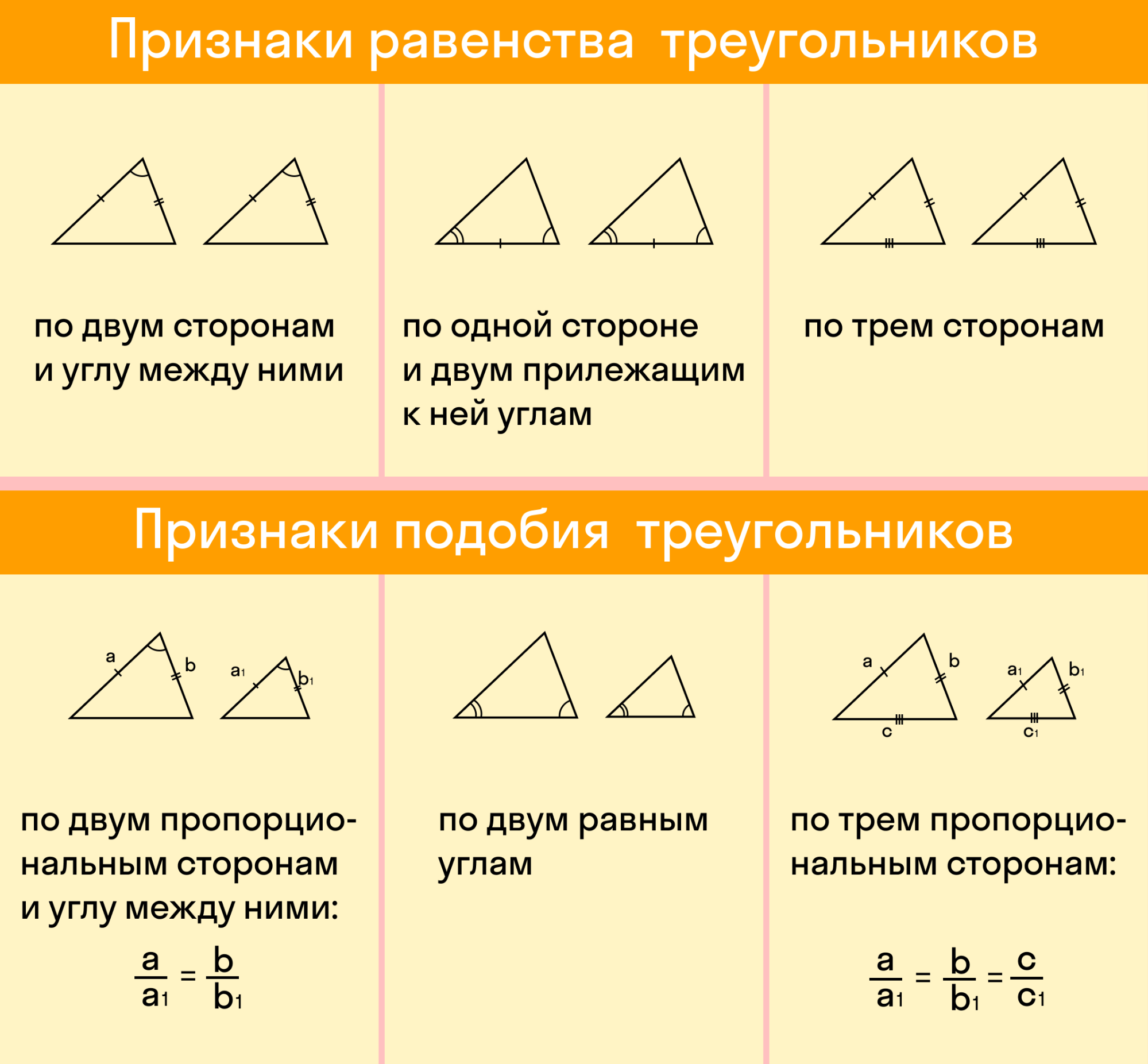
Первый признак равенства треугольников звучит так:

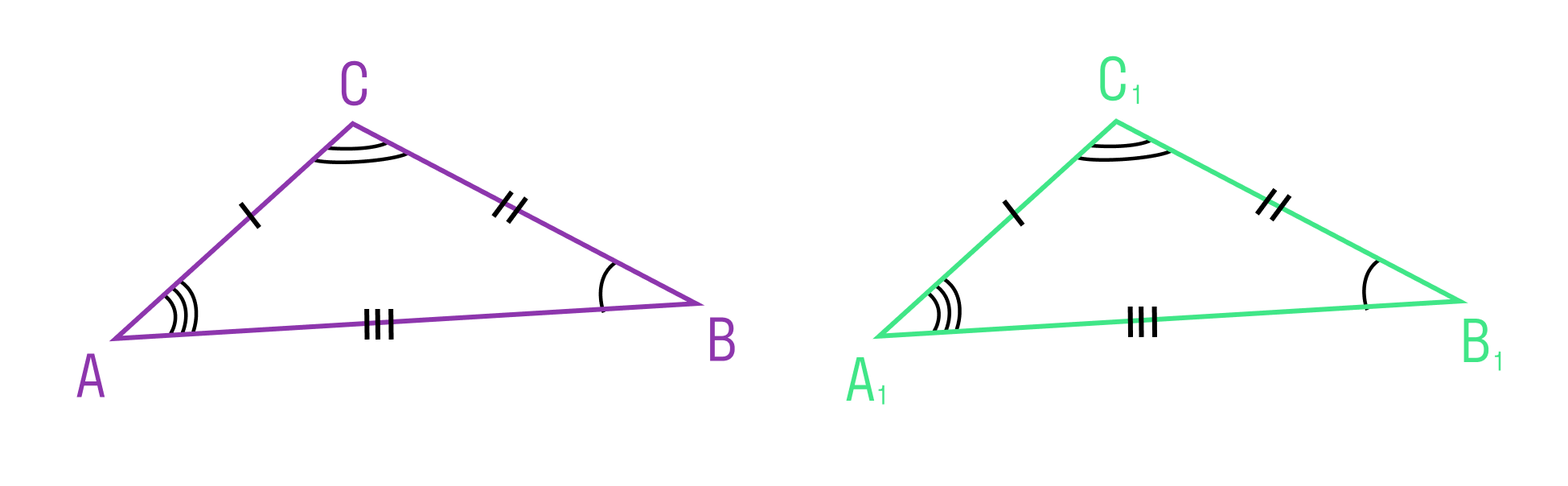
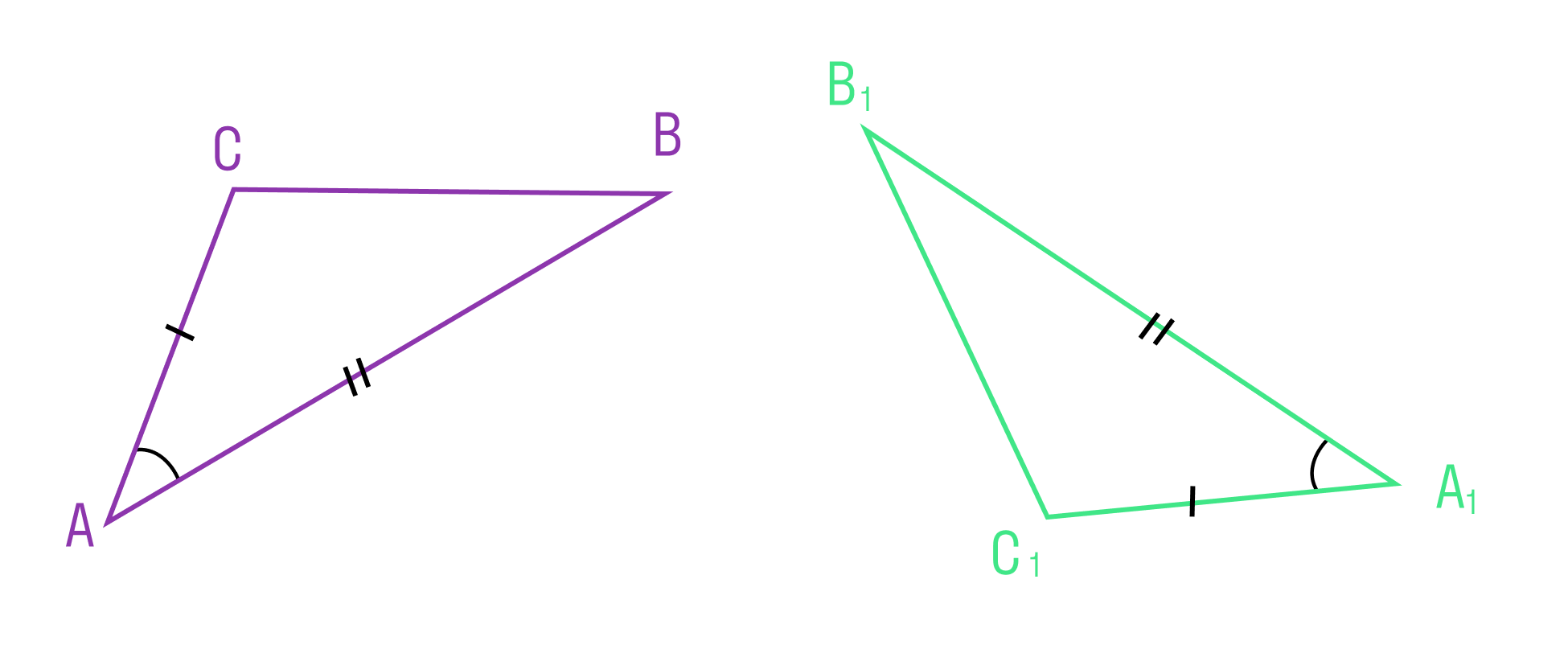
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны

Второй признак равенства треугольников

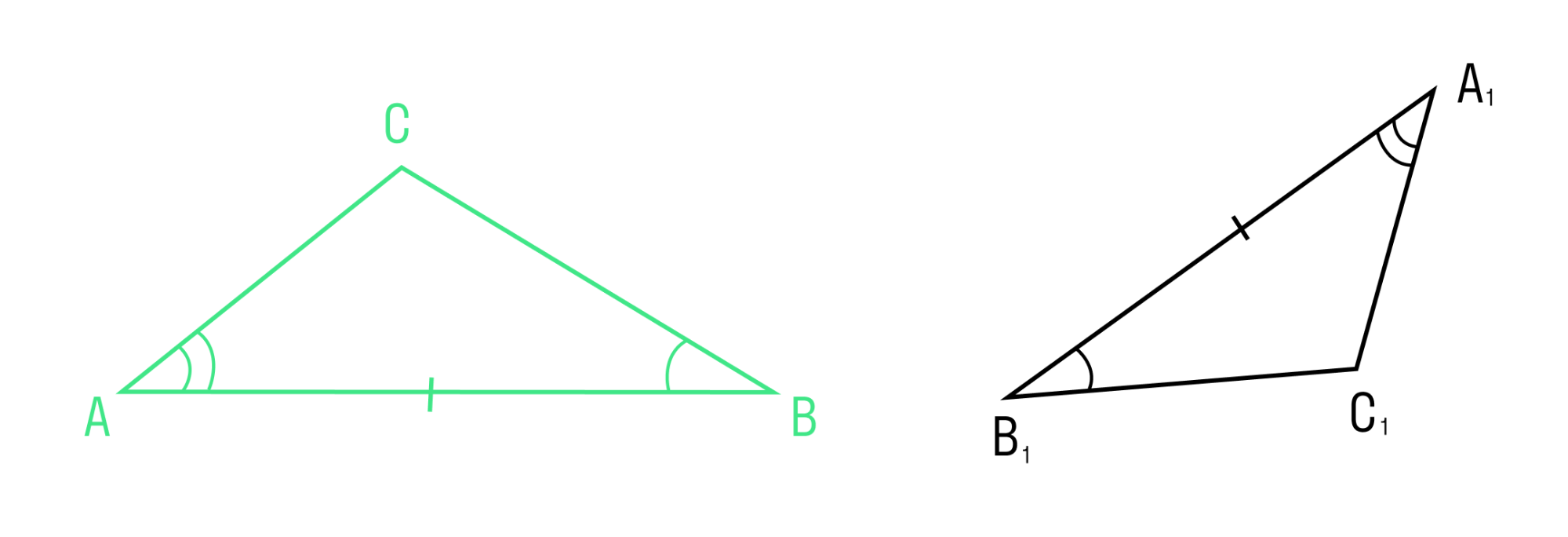
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Третий признак равенства треугольников

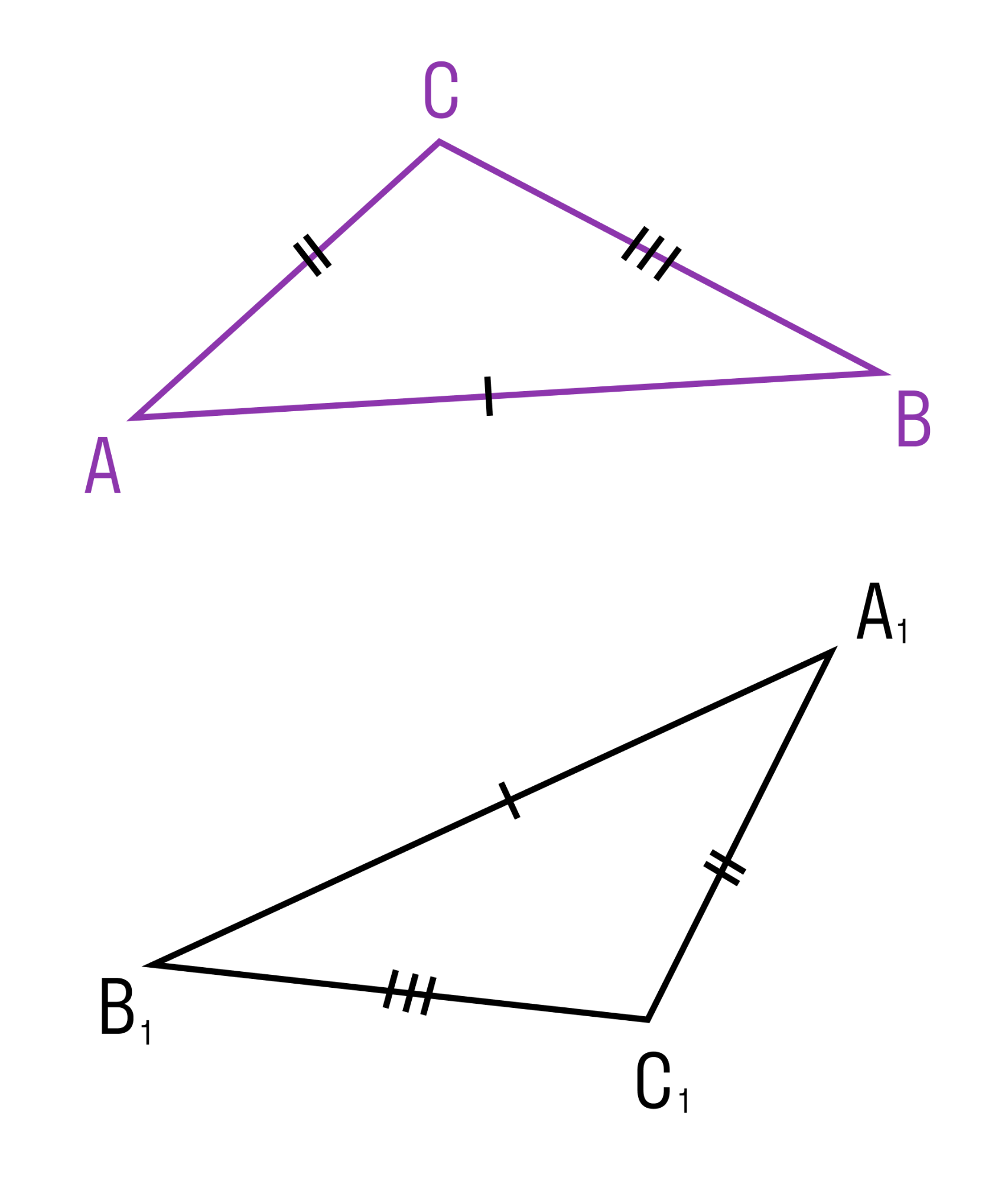
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Из теоремы следует, что треугольник — жесткая фигура, то есть фигура, которую невозможно деформировать.

Подобные треугольники

Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.

Треугольники АВС и A₁B₁C₁ будут подобны, если

Число k, которое равно отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.

Подобие треугольников обозначают специальным символом — ∾. На рисунке треугольники АВС и A₁B₁C₁ подобны, это можно записать так: ΔАВС ∾ ΔA₁B₁C₁.

Теорема о первом признаке подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такое треугольники подобны.

Второй признак подобия треугольников

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны — такие треугольники подобны.

Третий признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

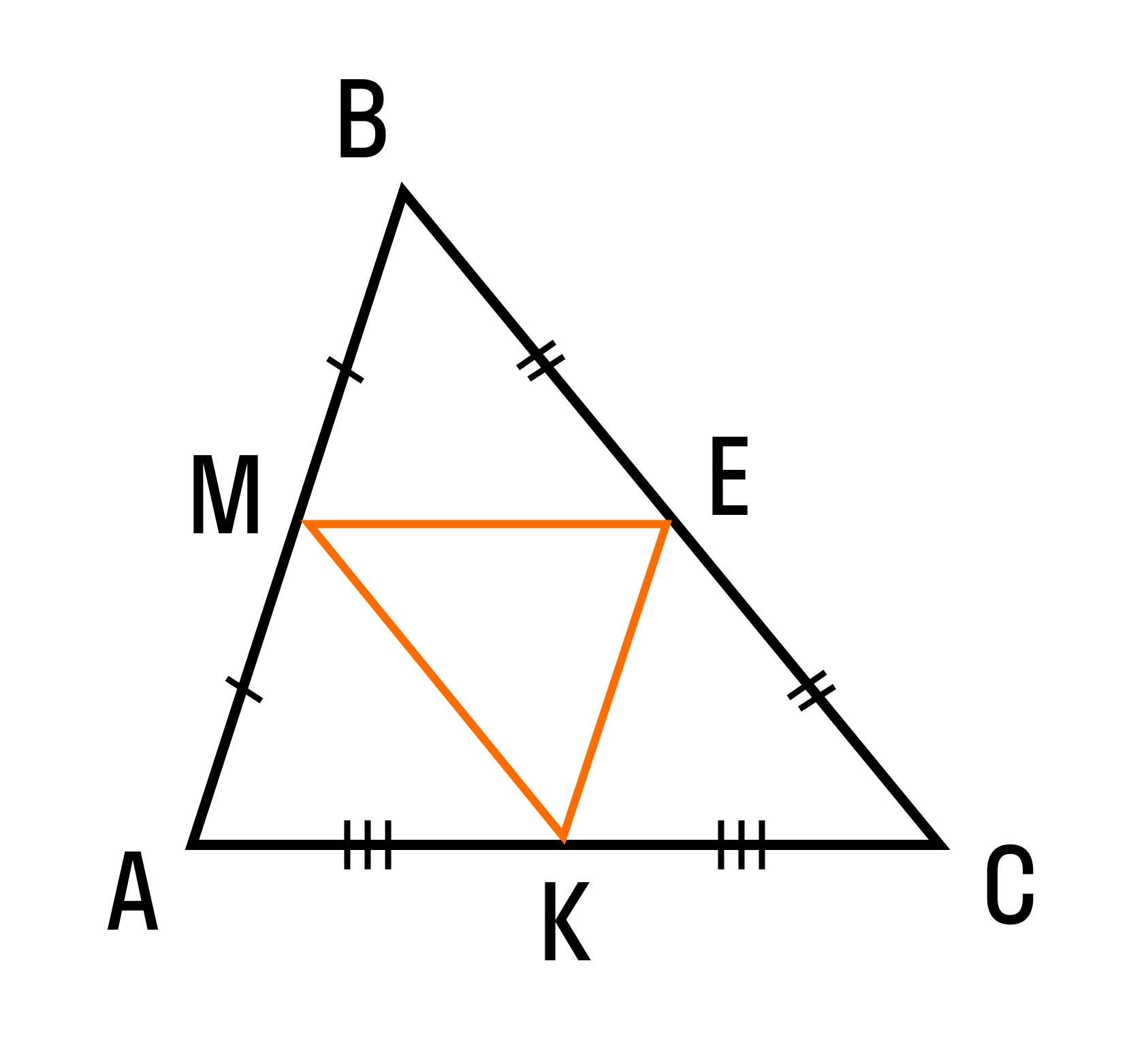
Средняя линия треугольника — это отрезок, который соединяет середины двух его сторон. В каждом треугольнике можно провести три средних линии, при пересечении которых получается четыре равных треугольника, подобных исходному с коэффициентом подобия 1/2.

На рисунке изображен треугольник АВС. Отрезки МЕ, МК и КЕ — средние линии данного треугольника, ΔВМЕ = ΔАМК = ΔСЕК = ΔМЕК.

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

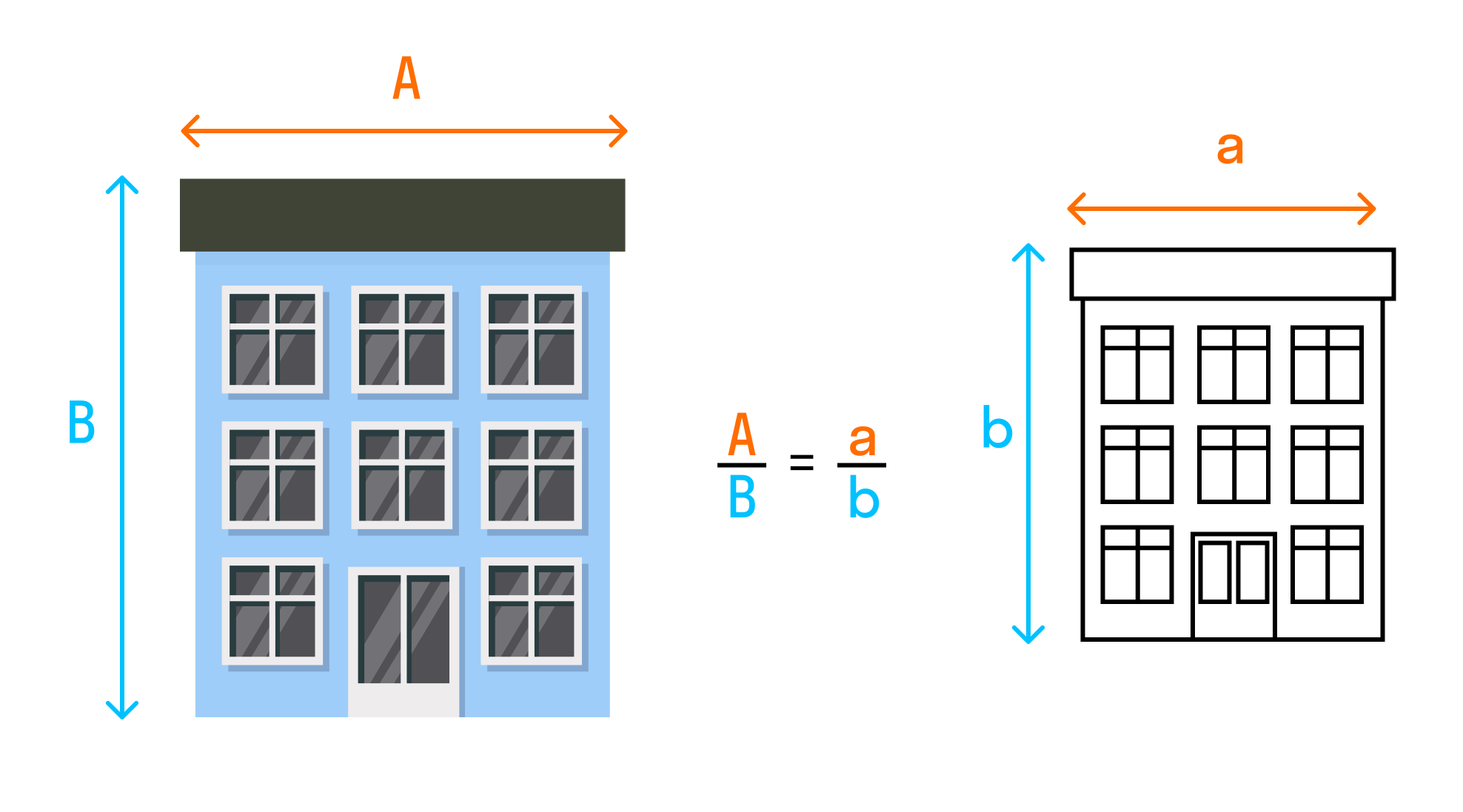
Важно понимать, что подобие в математике — это то, что в обычной жизни мы называем схожестью. Нарисовали треугольники или прямоугольники и говорим, что они похожи потому, что их стороны пропорциональны.

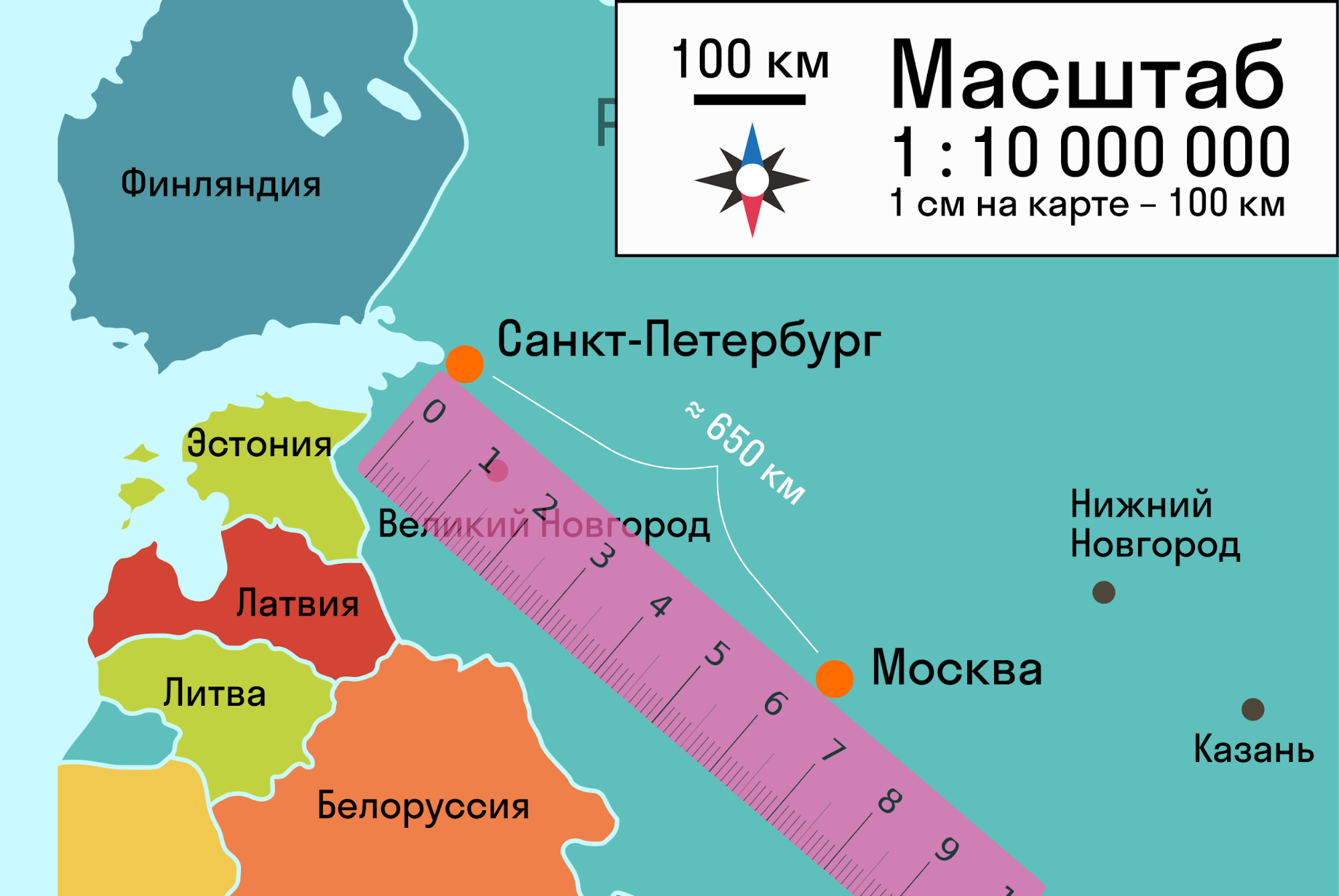
Пример подобия — карта. Она подобна местности, которую отражает. А масштаб — это и есть коэффициент подобия. С треугольниками или другими фигурами точно также.

Классификация треугольников по их сторонам

Для классификации треугольников можно использовать их типологию.

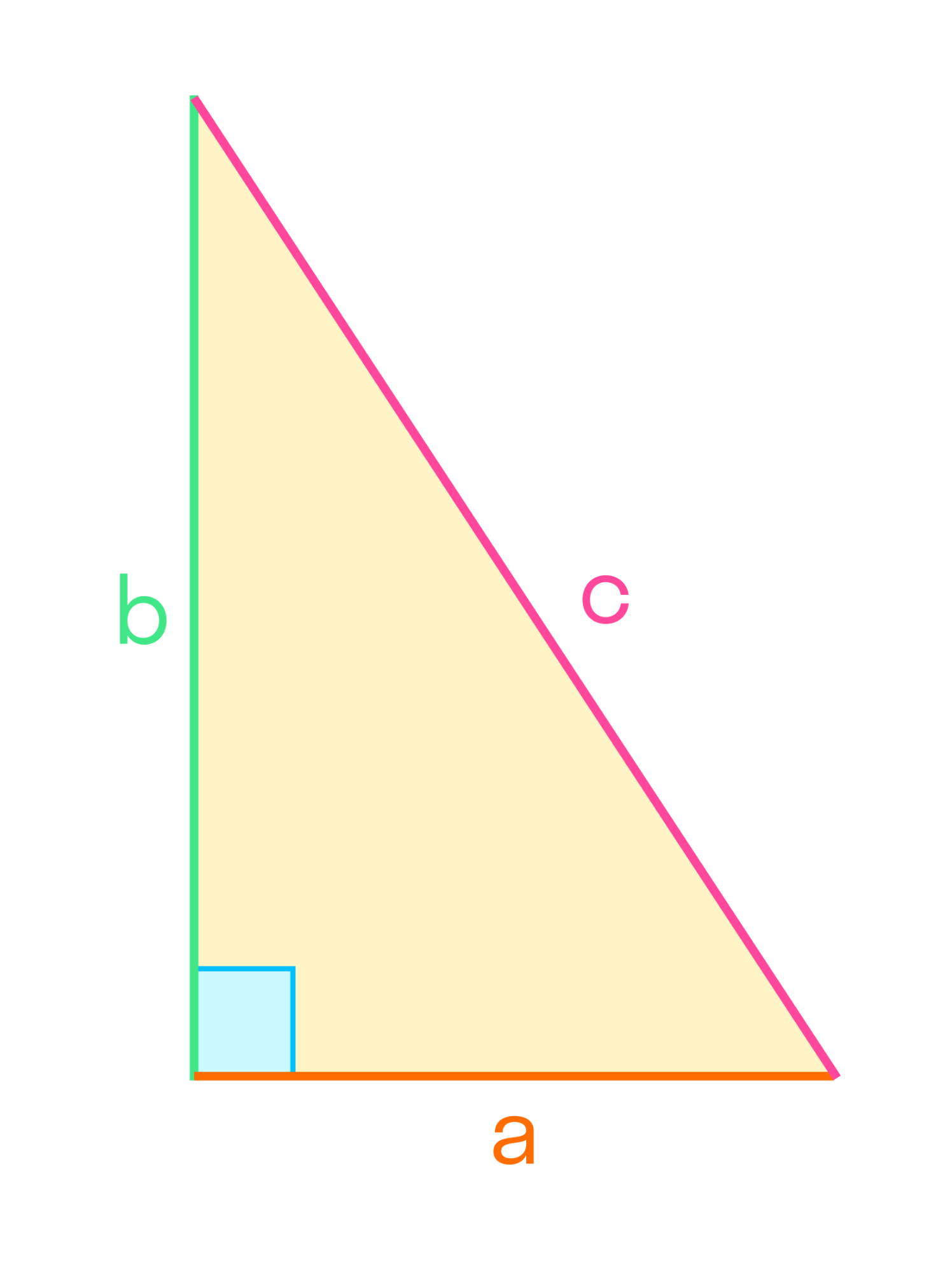
Один из распространенных типов — прямоугольный треугольник. Если один из углов прямой, то это накладывает определенные свойства на треугольник. Прямоугольный треугольник — это также половина прямоугольника.

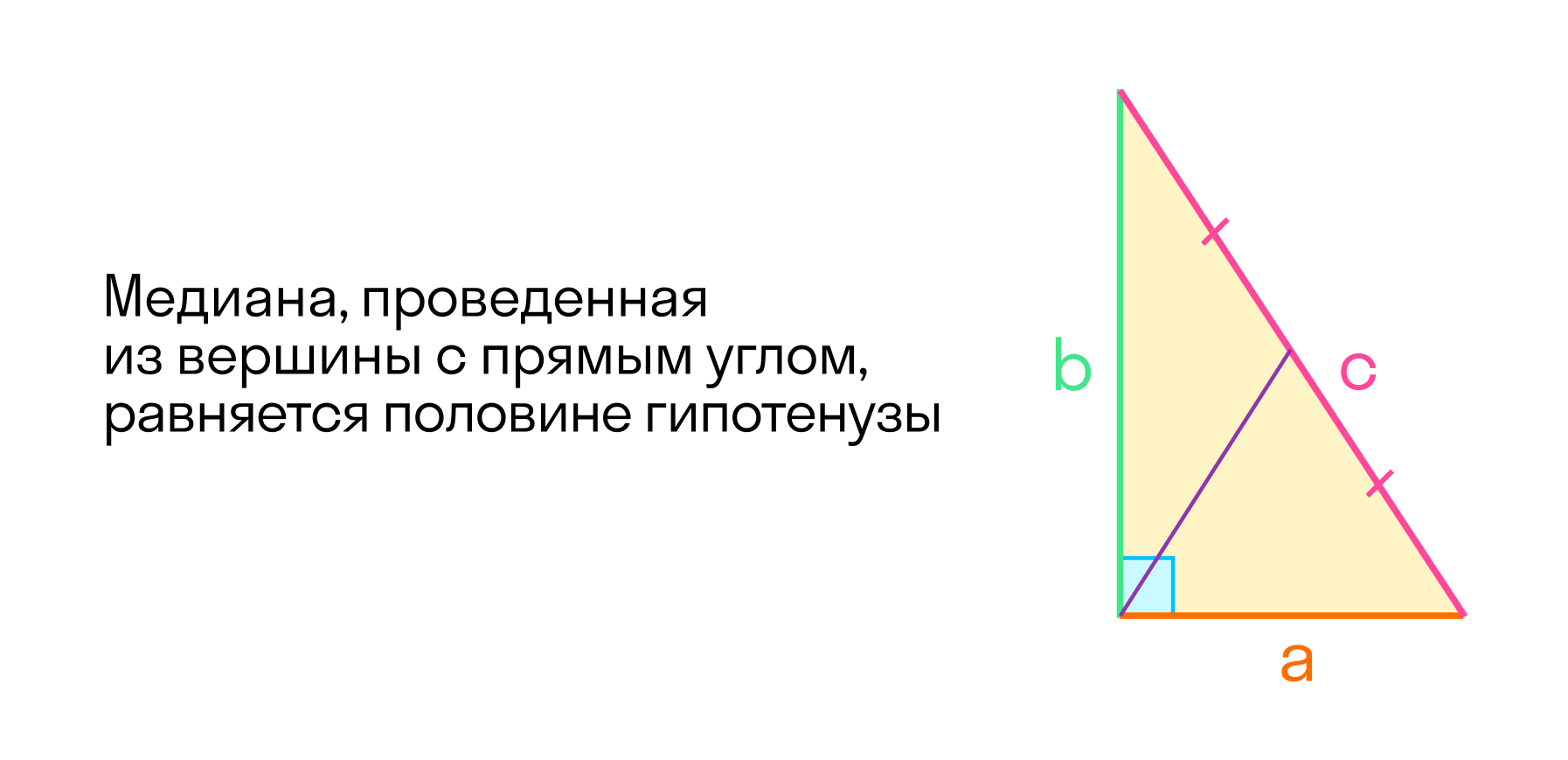
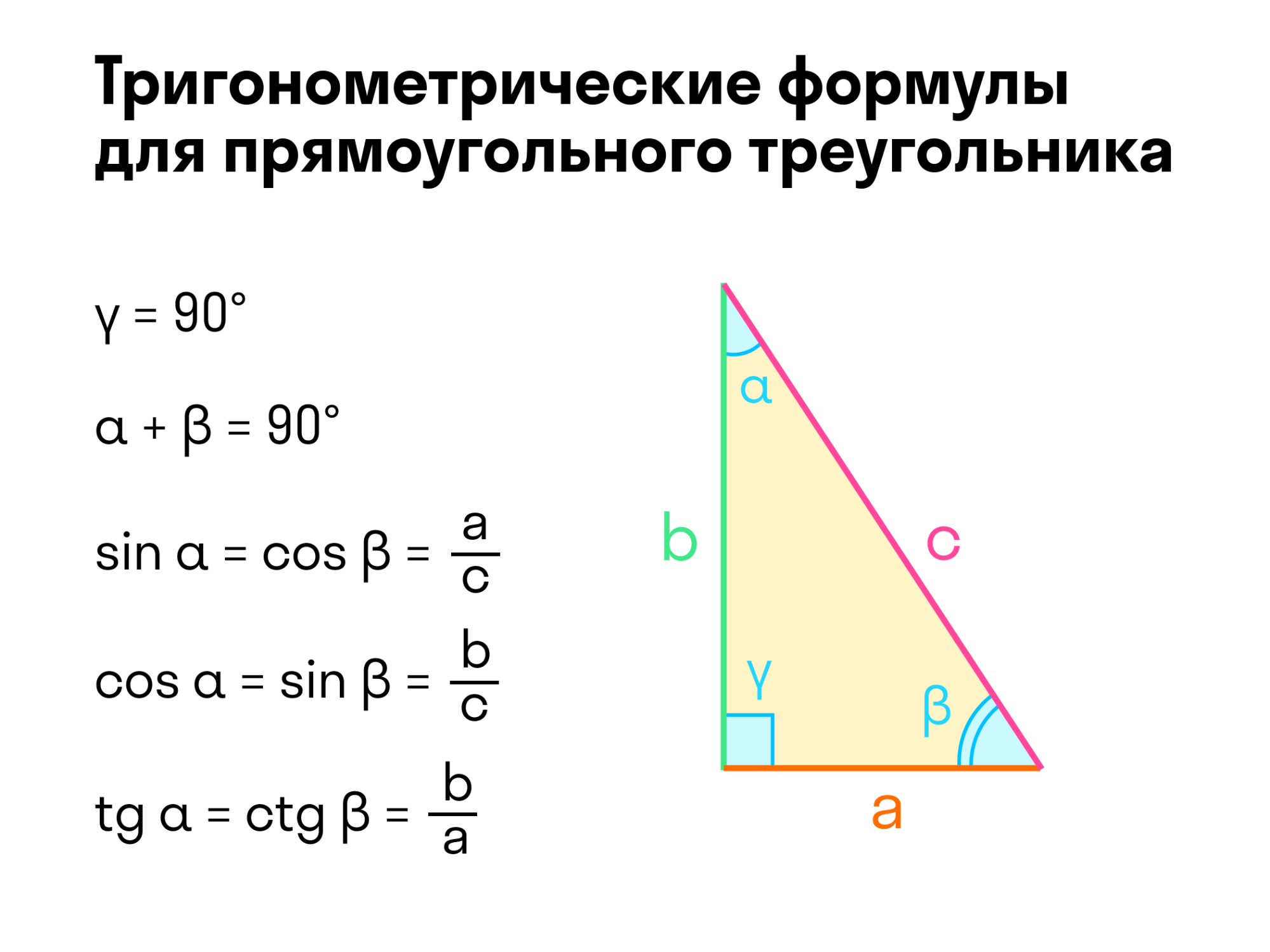
Свойства прямоугольного треугольника

С прямоугольных треугольников начинается изучение тригонометрии. Можно измерять углы с помощью отношений, использовать понятия синуса, косинуса. Помним, что угол можно задать двумя числами, их отношением.

Если две стороны треугольника равны, то это равнобедренный треугольник — и тогда у него есть ось симметрии. Если нарисовать такой треугольник и сложить лист пополам, то две части треугольника совпадут. Эта особенность дает треугольнику определенные свойства.

Симметричный треугольник, у которого все углы и стороны равны — это равносторонний треугольник. У таких треугольников три оси симметрии. Это значит, что если мы повернем треугольник на 60 градусов, то получим точно такой же треугольник.

Такой треугольник задается одним параметром — длиной стороны. Она полностью определяет все другие значения и размеры в этом треугольнике.

От правильного треугольника может плавно перейти к правильным многоугольникам. У треугольника 3 угла, у четырехугольника — 4, а у пятиугольника — 5 углов. У многоугольника много углов🙃

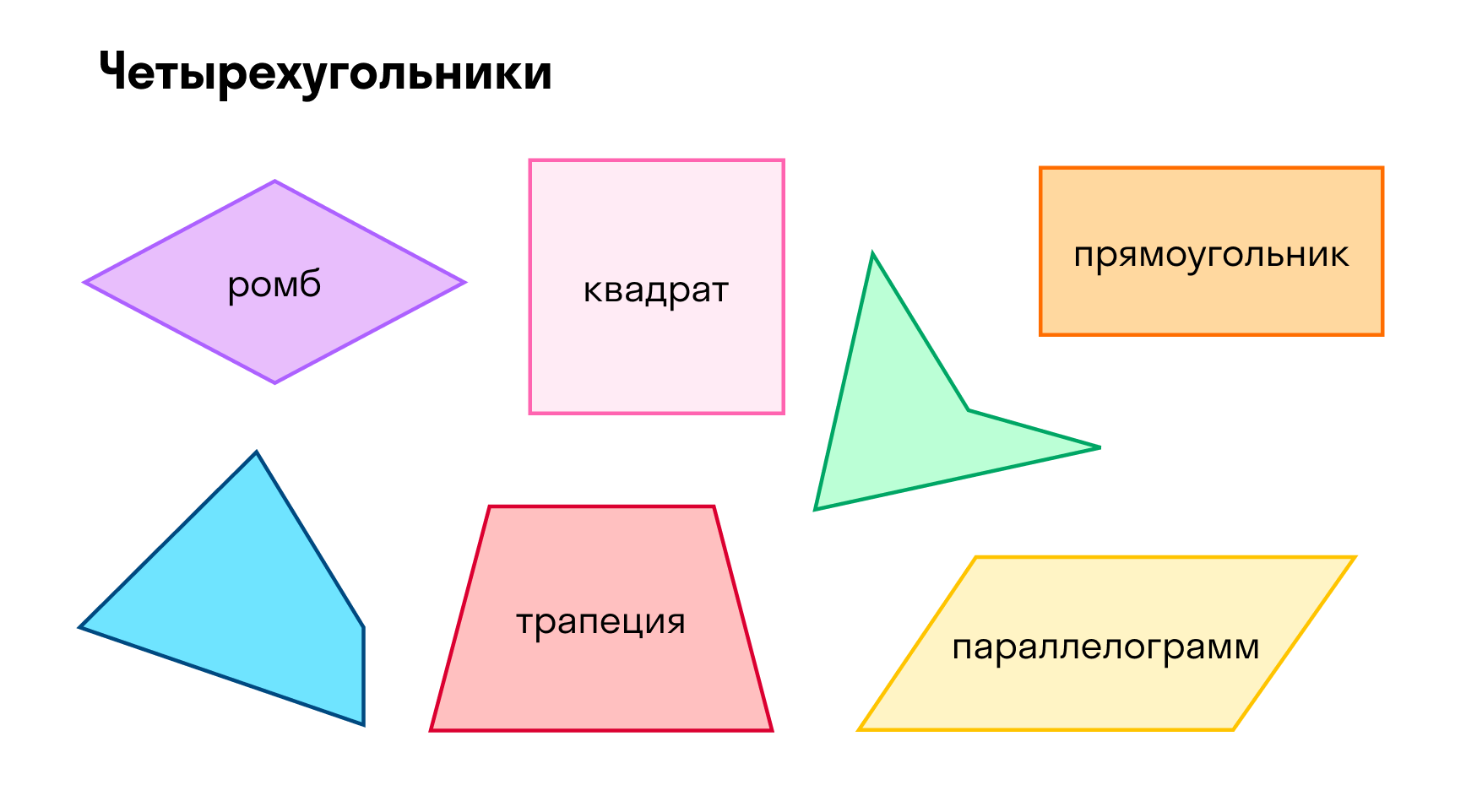
Четырехугольники

Про четырехугольники мы много говорим на уроках в школе: прямоугольник, квадрат, ромб.

Но говорим о них не в общем случае, как для треугольников (такие вещи, как теорема синусов, косинусов), а можем формулировать только какие-то свойства для определенных видов четырехугольников.

Четырехугольникам лучше уделить побольше времени — у каждого из них есть особые свойства, которые не пригодятся для других фигур. Поэтому каждый четырехугольник лучше внимательно изучить на уроке или почитать в наших материалах:

Окружность

Окружность — это еще один объект, который полезно изучить. Ее легко описать, она задается одним параметром — радиусом. А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.

Взаимодействие объектов

Следующий уровень — это взаимодействие всех-всех объектов, о которых мы говорили раньше.

Например, окружность и прямая. Прямая может находиться где-то в стороне от окружности, может ее пересекать, а может касаться, то есть пересекать в одной точке.

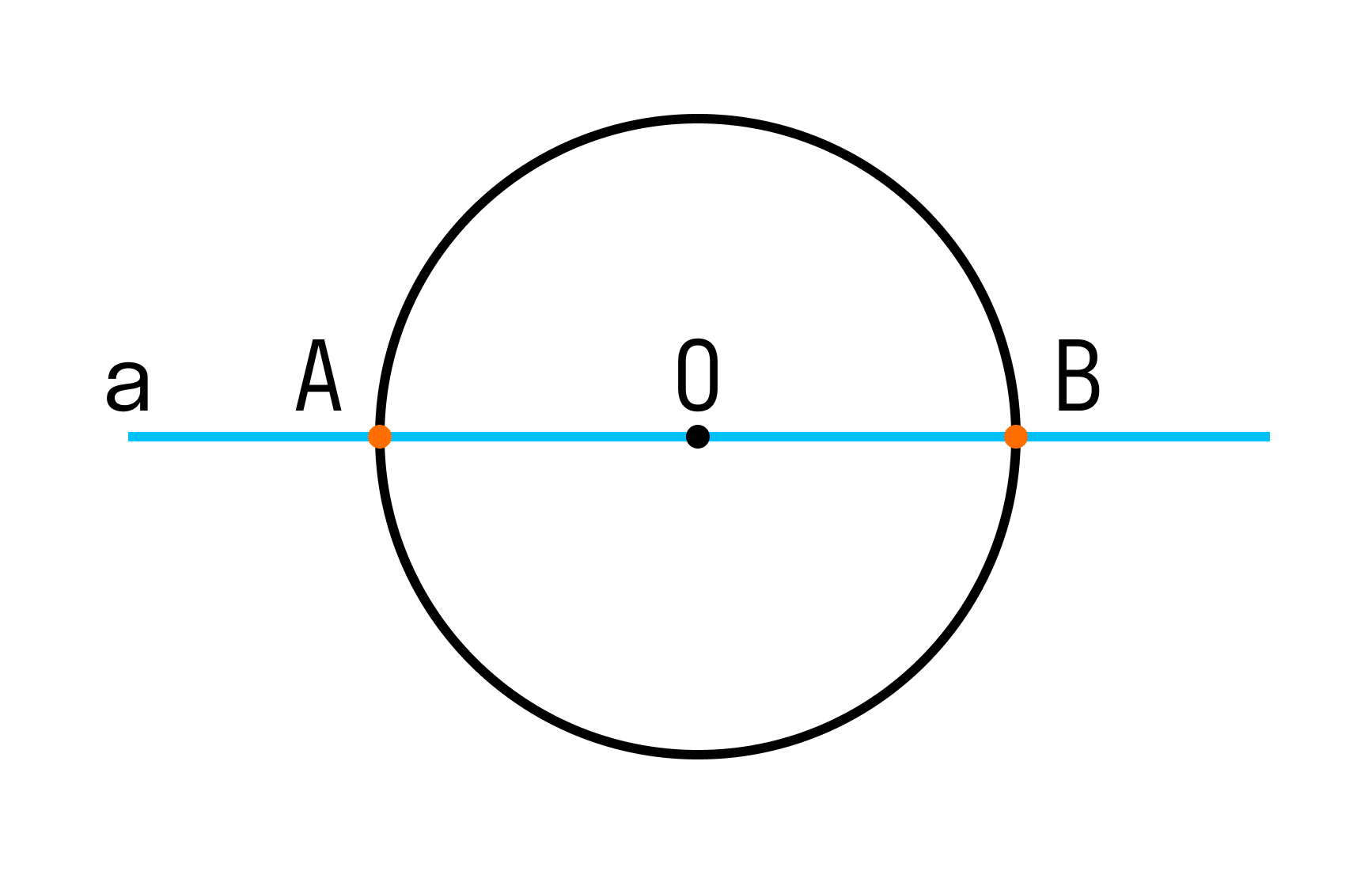
Если прямая проходит через центр окружности, то она пересекает окружность в двух точках — концах диаметра, который лежит на на этой прямой.

На рисунке прямая a проходит через центр окружности (точку О) и пересекает ее в двух точках А и В, которые являются концами диаметра АВ данной окружности.

Если прямая a не проходит через центр О окружности радиуса r, то возможны три случая взаимного расположения прямой и окружности — в зависимости от соотношения между радиусом r этой окружности и расстоянием d от центра окружности до прямой a. Вот эти случаи:

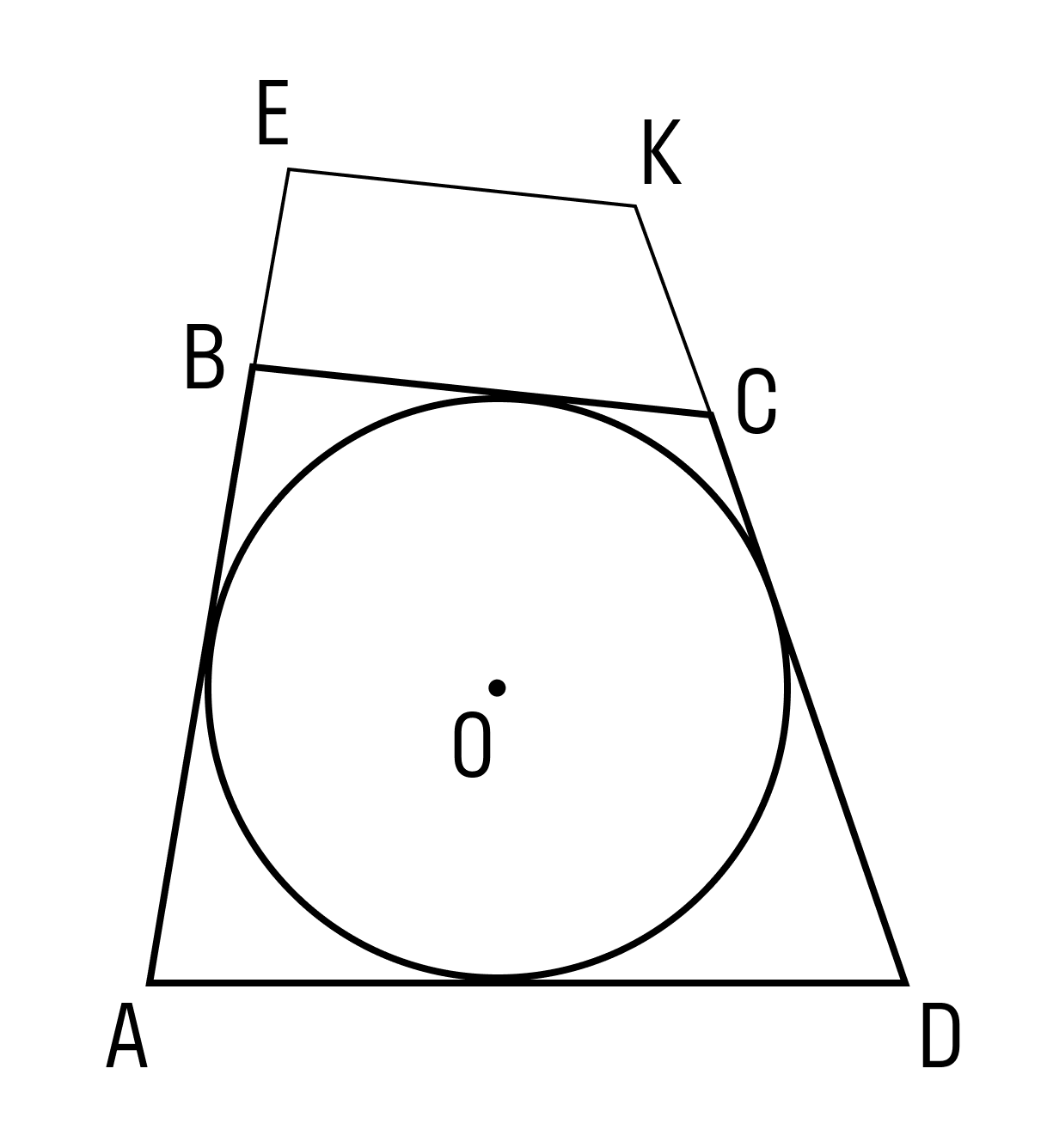
Окружность вписанная в многоугольник — это окружность, которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана. Описанный около окружности многоугольник — это многоугольник, в который вписана окружность.

На рисунке четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.

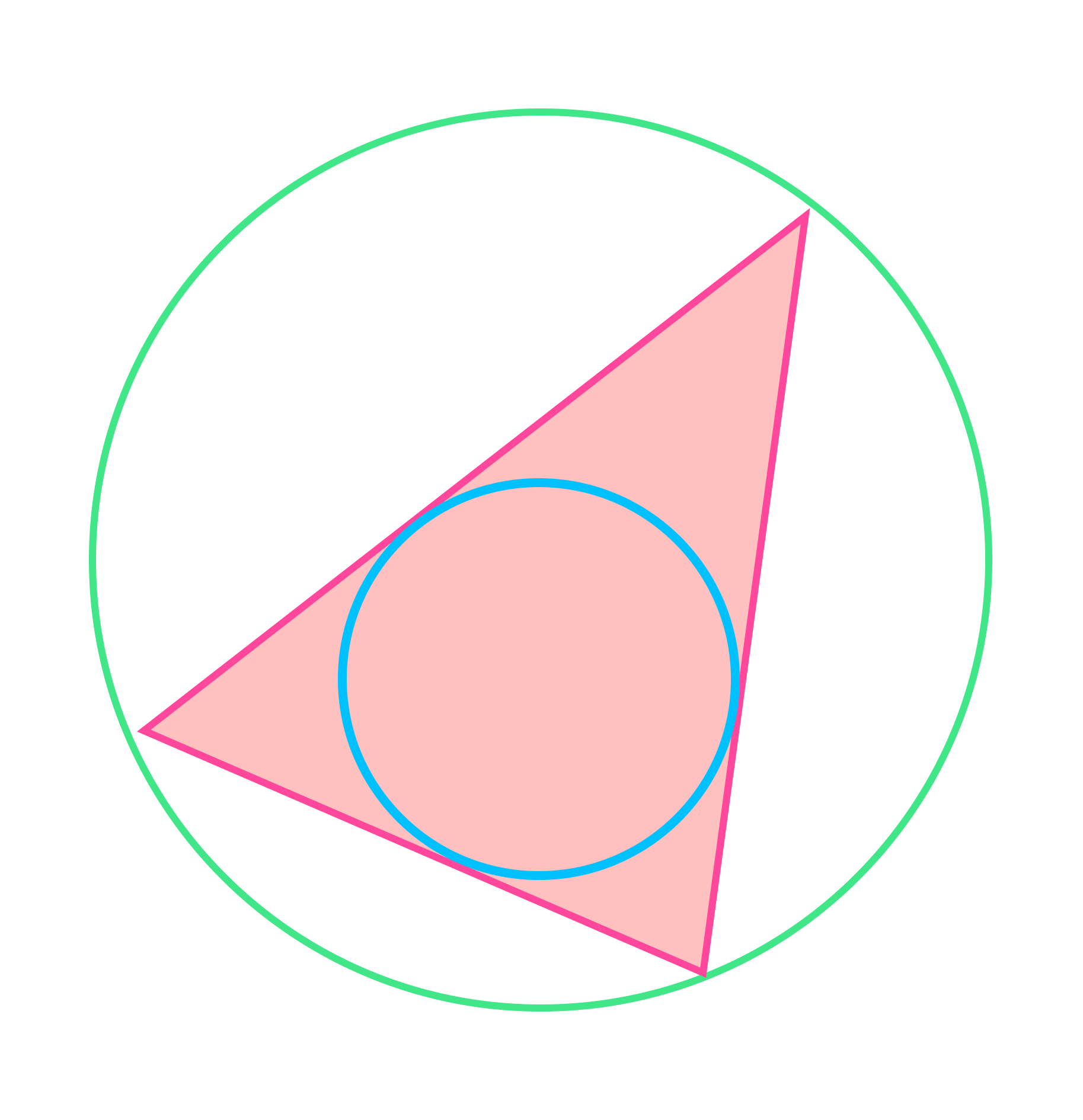
В любой треугольник можно вписать только одну окружность, и вокруг любого ее можно описать.

Все это верно только для треугольников. Не в любой четырехугольник можно вписать окружность, и не вокруг любого можно описать. Более подробно эту тему можно изучить на уроках математики: признаки, теоремы и правила.

Практическая сторона геометрии

Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.

Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.

А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.

Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.

Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.

Почему изучать геометрию сложно: некоторые правила придется учить наизусть.

Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество. Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней.

Источник