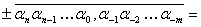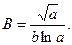Что значит цифра верная в строгом широком смыслах
Что значит цифра верная в строгом широком смыслах
Раздел 1. Приближенные числа и действия над ними
1.1 Виды погрешностей при приближенных вычислениях
Точное решение некоторых математических задач невозможно получить классическими методами, или это решение может быть получено в таком сложном виде, что неприемлемо для дальнейшего практического использования. Кроме того, точное решение задачи может потребовать очень большого количества (от нескольких десятков до многих миллиардов) действий. В таких случаях прибегают к приближенным и численным методам решения.
Появление компьютеров значительно расширило область применения этих методов. В настоящее время трудно себе представить инженера, не владеющего компьютером и методами приближённых вычислений.
Заметим, что любой компьютер способен запоминать большие, но конечные массивы чисел и производить над ними арифметические операции и сравнения с большой, но конечной скоростью. То есть машина способна выполнять очень большое, но конечное число операций. Поэтому при работе на компьютере можно использовать только те математические модели, которые описываются конечным набором чисел, и использовать только конечные последовательности арифметических действий.
Математическими моделями различных явлений служат функции, производные, интегралы, дифференциальные уравнения и т.п. При работе на компьютере эти исходные модели следует заменить такими, которые описываются конечными наборами чисел с указанием конечной последовательности действий для их обработки. Для этого функцию заменяют таблицей, определённый интеграл — суммой и т.д. Кроме того, вычислительная машина обладает конечной памятью и может оперировать с числами конечной длины, поэтому промежуточные результаты округляются. В результате этого даже точный метод с конечным числом действий становится приближенным.
Таким образом, решение, полученное численным методом, является приближенным.
Причинами появления погрешностей являются:
Погрешность решения, вызванная первыми двумя причинами, называется неустранимой — она не зависит от математика.
Погрешность метода возникает потому, что численным методом, как правило, решается не исходная задача, а более простая. Кроме того, обычно численный метод основан на бесконечном процессе, который приходится обрывать на некотором шаге.
Большинство численных методов зависит от одного или от нескольких параметров. Выбор параметров метода позволяет регулировать погрешность метода.
Погрешность округлений не должна быть существенно больше погрешности метода. А погрешность метода целесообразно выбирать в 2-5 раз меньше неустранимой погрешности.
1.2 Приближенные числа
Определение 1.2. Относительной погрешностью приближенного числа a * называется величина:
Любое число d ( a * ) , удовлетворяющее неравенству
Верные и сомнительные цифры приближенного значения числа.
Значащие цифры приближенного значения числа
При вычислениях часто трудно указать наряду с приближенными значениями их погрешности. А в различных справочниках указывать погрешности приближенных данных неудобно, неэкономично. Поэтому при записи приближенных значений чисел требуют, чтобы по этой записи можно было определить границу абсолютной погрешности приближения. Для этого вводится понятие верной и сомнительной цифр приближенного значения числа.
Определение: Цифра называется верной, если граница абсолютной погрешности данного приближенного значения числа не превосходит (£) единицы того разряда, в котором записана эта цифра. В противном случае цифра называется сомнительной.
Пример: Определить верные и сомнительные цифры в приближенном значении числа:
1. х = 35,4 ± 0,08
Вывод: Если в записи приближенного значения числа какая-то цифра – верная, то и все предшествующие ей цифры так же являются верными.


Цифра 8 в 0,1; h = 0,04 £ 0,1; 8 – верная цифра;
Следовательно, 9 – верная цифра.
Цифра 7 в 0,01; h = 0,03 £ 0,01; 7 – сомнительная цифра;
Цифра 6 в 0,1; h = 0,03 £ 0,1; 6 – верная цифра;
Следовательно, 5, 4, 9 – верные цифры.
При записи приближенных чисел принято соблюдать следующие правила.
Правила записи приближенных чисел:
Пример: Записать правильно приближенное значение числа:
1. х = 950,031 ± 0,04
Следовательно, 0, 5, 9 – верные цифры.
х » 950,0 (правила 1, 2)
2. х = 0,075 ± 0,000005
х » 0,07500 (правила 1, 2)

Следовательно, 0, 6, 4, 7 – в. ц.
х » 74600 × 10 4 (правила 1, 3)
Если приближенное значение числа дано без указания границы абсолютной погрешности, то ее можно определить по записи этого приближенного значения, используя определение верной и сомнительной цифр приближенного значения числа.
Пример:
1. Указать абсолютную погрешность приближенного числа а = 3,14.
Решение:
Дата добавления: 2017-01-29 ; просмотров: 40560 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Что значит цифра верная в строгом широком смыслах
Формы записи приближенных чисел
Приближенные числа записываются либо в виде конечных десятичных дробей, либо в виде целых чисел.
Замечание 1. Определение естественной (позиционной, с фиксированной точкой) формой записи целого числа дается аналогично.
В связи с этим имеет место следующее определение.
Определение 2. Значащими цифрами приближенного числа называются все цифры его записи, начиная с первой ненулевой слева.
Пример 4. У числа 0,0046 только две значащих цифры: 4 и 6.
Пример 5. У числа 0,004600 четыре значащих цифры: 4, 6 и два последних нуля. (Для чего оставляют нули в конце числа, будет рассмотрено позднее).
Если приходится работать с большим количеством приближенных чисел, то запись 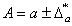
Определение 4. Цифра приближенного числа называется верной в узком смысле, если абсолютная (предельная абсолютная) погрешность этого числа не превосходит половины единицы десятичного разряда, соответствующего этой цифре, в противном случае сомнительной в узком смысле.
В связи с рассмотренным примером возникает следующий вопрос: «Как отличить приближенное число 34200 с двумя последними сомнительными нулями от точного числа 34200?»
Правила записи приближенных чисел.
1. Приближенные числа записываются в форме х ± Dх. Запись X = х ± Dx означает, что неизвестная величина X удовлетворяет следующим неравенствам: x-Dx
D(X-Y) = 0,005 + 0,005 = 0,01.
 |
Относительную погрешность получим по формуле связи:
2. Умножение и деление. Если dХ
Существуют строгие и нестрогие методы оценки точности результатов вычислений.
1. Строгий метод итоговой оценки. Если приближенные вычисления выполняются по сравнительно простой формуле, то с помощью формул Ф.1-Ф.5 и формул связи погрешностей можно вывести формулу итоговой погрешности вычислений. Вывод формулы и оценка погрешности вычислений с ее помощью составляют суть данного метода.
ПримерЗначения a = 23,1 и b = 5,24 даны цифрами, верными в строгом смысле. Вычислить значение выражения
С помощью МК получаем В = 0,2921247. Используя формулы относительных погрешностей частного и произведения, запишем:

Пользуясь МК, получим 

2. Метод строгого пооперационного учета погрешностей. Иногда попытка применения метода итоговой оценки приводит к слишком громоздкой формуле. В этом случае более целесообразным может оказаться применение данного метода. Он заключается в том, что оценивается точность каждой операции вычислений отдельно с помощью тех же формул Ф.1-Ф.5 и формул связи.
3. Метод подсчета верных цифр. Данный метод относится к нестрогим. Оценка точности вычислений, которую он дает, в принципе не гарантирована (в отличие от строгих методов), но на практике является довольно надежной. Суть метода заключается в том, что после каждой операции вычислений в полученном числе определяется количество верных цифр с помощью нижеследующие правил.
П.1. При сложении и вычитании приближенных чисел в результате верными следует считать, те цифры, десятичным разрядам которых соответствуют верные цифры во всех слагаемых. Цифры всех других разрядов кроме самого старшего из них перед выполнением сложения или вычитания должны быть округлены во всех слагаемых.
П.2. При умножении и делении приближенных чисел в результате верными следует считать столько значащих цифр, сколько их имеет приближенное данное с наименьшим количеством верных значащих цифр. Перед выполнением этих действий среди приближенных данных нужно выбрать число с наименьшим количеством значащих цифр и округлить остальные числа так, чтобы они имели лишь на одну значащую цифру больше него.
П.З. При возведении в квадрат или в куб, а также при извлечении квадратного или кубического корня в результате следует считать верными столько значащих цифр, сколько имелось верных значащих цифр в исходном числе.
Граница абсолютной погрешности
Вычислительная математика. Граница абсолютной погрешности
Абсолютная погрешность приближенного значения числа, граница абсолютной погрешности, верные и значащие цифры числа
Верные и значащие цифры числа. Округление чисел.
Наша система счета или счисления называется десятичной системой счисления, а 10 – основанием этой системы:
разряд единиц, разряд десятков, разряд сотен и т.д. Аналогично, разряды десятичных дробей: десятые, сотые, тысячные и т.д.
В приближенном числе различают верные и сомнительные цифры. Цифра какого-либо разряда приближенного числа а считается верной в широком смысле, если граница абсолютной погрешности числа а не превосходит единицы того разряда, в котором записана эта цифра.
Если же граница абсолютной погрешности больше единицы какого-либо разряда, то цифра этого разряда и все цифры, расположенные справа от нее считаются сомнительными. Граница абсолютной погрешности ∆а находится непосредственно по записи приближенного значения а числа х.
Например:
Приближенное значение 24,5
Граница абсолютной погрешности 0,3
Приближенное значение 375
Граница абсолютной погрешности 20
Когда рассматриваем верные цифры в широком смысле, то достаточно посмотреть на границу абсолютной погрешности и взять цифры приближенного числа, которые на разряд больше, чем граница абсолютной погрешности.
Цифра какого-либо разряда приближенного числа а считается верной в строгом смысле, если граница абсолютной погрешности числа а не превосходит половины единицы того разряда, в котором записана эта цифра. Если же граница абсолютной погрешности больше половины единицы какого-либо разряда, то цифра этого разряда и все цифры, расположенные справа от нее считаются сомнительными.
В числах, полученных в результате измерений или вычислений и используемых при расчётах в качестве исходных данных, а также в десятичной записи приближенного значения числа, все цифры должны быть верными.
Значащими цифрами приближенного числа, выраженного десятичной дробью считаются все верные цифры этой дроби, кроме нулей, стоящих перед первой цифрой (слева направо), отличной от нуля.
Например:
Приближенное число 10,408 имеет 5 значащих цифр, так как крайняя слева цифра числа отлична от нуля (она равна 1)
Приближенное число 0,01104 имеет 4 значащие цифры:1, 1, 0, 4. Два нуля, стоящие слева от 1 не считаются значащими цифрами
Приближенное число 0,030 имеет 2 значащие цифры: 3 и 0 справа, по правилу два нуля, стоящие слева от цифры 3, не относятся к значащим.
Значащими цифрами приближенного целого числа считаются все его цифры, кроме нулей, поставленных взамен отброшенных или
Например: Частное
Число 6000 имеет 3 значащие цифры, так как один последний нуль поставлен вместо отброшенной цифры (единицы).
Округление чисел. При округлении числа а его заменяют числом а1 с меньшим количеством значащих цифр. Абсолютная величина разности
| а – а1 | называется погрешностью округления.
При применении этого правила погрешность округления не превосходит половины единицы десятичного разряда, определяемого последней оставленной значащей цифрой.
Округление приближенных значений чисел с сохранением в записи только верных цифр производится до разряда, в котором записана первая справа верная цифра.
Например:
Округлите до первого справа верного разряда приближенные значения данных чисел:
Граница абсолютной погрешности 0,05 (разряд – сотые) цифры справа налево:1 – сомнительная, 8 – сомнительная, 2 – сомнительная, 3 – верная цифра 3