Что значит трехзначное число
Математика
Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет
С этой картой можно накопить на мечту, жми ⇒
План урока:
Здравствуйте, ребята! Познакомьтесь с главной героиней сказки Александра Волкова «Волшебник Изумрудного города» девочкой Элли.
Злая колдунья наслала смерч на город Канзас, где жила ее семья. Домик вместе с девочкой и пёсиком сильным ветром перенесло в Волшебную страну. Представьте себе — ураган разрушил даже пословицу. Попробуйте догадаться, какие слова сдул ветер?
Правильно, это сто. Пословица объясняет, что настоящие верные друзья придут на помощь в любой ситуации.
Ребята, вы хотите получать пятерки по математике, а девочка мечтает вернуться к маме и папе. В Изумрудном городе живет волшебник Гудвин, который исполнит ваши желания. Но, чтобы дойти к нему по сказочной дороге из желтого кирпича, нужно немало потрудиться. На уроке научимся не только считать, но и поможем Элли, Тотошке и ее трем друзьям преодолеть препятствия, постараемся выполнить все задания.
Образование и название трехзначных чисел
Собачка Тотошка просит вас вспомнить известные единицы счета.
10 десятков образуют новую единицу – сотню.
Сотни считают также как единицы и десятки. При записи круглых сотен рядом с их количеством записывают два нуля.
Запомните названия трехзначных круглых чисел:
Десять сотен называют словом тысяча и записывают так: 1000.
При счете за круглым числом сто называют 101 (сто один), далее 102 (сто два), 103 (сто три). Каждое последующее число больше предыдущего на один. За 199 называют 200 (двести), далее 201 (двести один). За числом 999 (девятьсот девяносто девять) следует 1000 (одна тысяча).
Какое число выложено палочками на рисунке? Разобраться в этом нам поможет нумерационная таблица.
В названии трехзначного числа принята следующая последовательность: сначала называют сотни, потом десятки и последние — единицы. В таблице одна сотня, четыре десятка и шесть единиц. Читают трехзначное число слева направо: сто сорок шесть.
Рассмотрите следующий пример. Каждую цифру числа 536 напишем в разрядную таблицу:
Для того, чтобы прочитать 536, нужно назвать количество единиц каждого разряда, начиная с сотен, и название этого разряда: пять сотен (пятьсот), три десятка (тридцать), шесть (название разряда единиц не произносится).
Получается: пятьсот тридцать шесть.
Хорошо, ребята, с этим заданием мы справились, побежали дальше по дороге знаний.
Запись трехзначных чисел
Элли и Тотошка на своем пути встречают чучело. Соломенный Страшила хочет получить мозги, он и не подозревает, что на самом деле уже хорошо соображает. Страшила расскажет нам, как происходит образование трехзначных чисел.
Числа, состоящие из 3-х цифр, называют трехзначными. Записываются они позиционно. Цифра читается по месту, которое она занимает.
На рисунке палочками выложено сто двадцать пять.
Это — триста шесть, записывается – 306. На месте десятков нужно писать нуль.
На третьем рисунке восемь сотен и два десятка палочек.
Прочитайте – восемьсот двадцать – 820. Поскольку нет ни одной палочки, обозначающей единицы, на месте единиц пишут нуль.
Десятичная запись трехзначного числа
Запишите трехзначные числа: двести тридцать два, сто четыре, шестьсот семьдесят, восемьсот тридцать шесть.
Проверьте: 232, 104, 670, 836.
Увеличение и уменьшение чисел в 10 раз, в 100 раз
Ребята, вы уже знаете, что для уменьшения и увеличения числа в несколько раз надо разделить его или умножить. Но как сделать какую-то величину в 10, 100 раз больше или меньше? К нам на помощь спешит железный Дровосек. От Гудвина он хочет получить любящее сердце.
Давайте узнаем, как найти число больше или меньше данного в десять или сто раз. Нам понадобятся названия разрядов трехзначных чисел:
Напишите, например, – 7. Семерка – единицы первого разряда.
Припишите к семерке нуль – 70. Теперь получилась семерка из второго разряда десятков: семьдесят. Во сколько раз 70 больше 7? В десять раз.
Добавьте еще один нуль справа – 700. Что сейчас обозначает цифра семь?
Она обозначает сотни — семьсот. Сотня – это единица третьего разряда. Во сколько раз 700 больше 7? В сто раз.
Задачи на уменьшение и увеличение числа в несколько раз решаются действиями деления и умножения.
Задание 1.
Семь увеличить в десять раз – это семь умножить на десять. Получится семьдесят.
Мы дописали столько же нулей, сколько в числе 10.
Задание 2.
Семь умножьте на сто – увеличьте в сто раз. Сколько нулей напишите в произведении?
Столько же, сколько в числе 100. Два нуля.
Ответ: семьсот.
Выполните обратные действия.
Задание 3.
Запишите семьсот – 700. Цифра семь обозначает третий разряд сотен. Отбросьте один нуль – 70. Какое арифметическое действие понадобилось?
Решение:
Мы разделили на десять действием деления.
Отбросили столько же нулей, сколько их в десяти. 1 нуль.
Задание 4.
Отбросьте еще один нуль. Семерка стоит в первом разряде – разряде единиц.
Уменьшите 700 в сто раз. Сколько нулей убрали?
Решение:
Мы убрали столько же нулей, сколько в ста. Два нуля.
Молодцы, все задания выполнили. Теперь вы легко ответите на вопросы.
Как изменится число, к которому приписывают один нуль? Оно увеличивается в 10 раз.
Что нужно сделать, чтобы увеличить число в 100 раз? Приписать к нему два нуля.
Как изменяется круглое число, если справа отбрасывают один нуль? Оно уменьшается в 10 раз.
Как уменьшить число в 100 раз? Убрать два нуля.
Ребята, будьте внимательны и осторожны. Вот в сказке девочка обогнала спутников и попала в плен к Людоеду.
Для спасения Элли выполните задание: сравните 10 см 2 и 1 дм 2
Рассуждайте так. Мы помним, что 1 дм = 10 см. Один квадратный дециметр – это квадрат со стороной один дециметр или десять сантиметров.
Как узнать площадь прямоугольника? Надо перемножить одну сторону на другую. Умножить на 10 – к множителю приписать один нуль. Получается сто.
10 см ∙ 10 см = 100 см 2
Значит, 1 дм 2 = 100 см 2
Теперь можем сравнить. Ответ: 1 дм 2 > 10 см 2
Вы справились с этим заданием. Элли спасена. Друзья побежали дальше и встретили льва.
Представление трехзначных чисел в виде суммы трехзначных слагаемых
Трусливый Лев мечтает добыть смелость, поэтому соглашается участвовать во всех заданиях и приключениях.
Все натуральные числа, состоящие из нескольких цифр, можно представить в виде суммы разрядных слагаемых. Чтобы правильно записать сумму, надо понять из каких разрядов состоит число.
257 — это трехзначное число.
В нем две сотни, пять десятков, семь единиц.
Также существует такое понятие, как разрядные единицы. Это 1, 10, 100 и т.д. В таблице три счетные единицы:
Каждая следующая счетная единица в 10 раз больше предыдущей единицы. Поэтому наша система счета называется десятичной.
Величины можно представить разными счетными единицами.
Допустим, есть сто десять. 110 единиц или 11 десятков.
110 = 110 ед. = 11 дес.
110 образовалось из одной сотни и одного десятка.
110 = 110 ед. = 11 дес. = 1 сот. 1 дес.
Следующий пример:
235 = 235 ед. = 23 дес. 5 ед. = 2 сот. 3 дес. 5 ед.
Задание 1.
Представьте число 432 в сумме разрядных слагаемых.
В нем четыре сотни, три десятка и две единицы.
Задание 2.
В числе 504 пять сотен и четыре единицы. В нем нет десятков. В таком случае на месте десятков пишут нуль.
Сумма разрядных слагаемых числа 504 записывается так:
Задание 3.
Запишите число, в котором шесть сотен и три десятка.
Рассуждайте так:
В числе нет единиц. В таком случае на месте единиц пишут нуль.
Это шестьсот тридцать. Разложите его на разрядные слагаемые.
Задание 4.
Число из семи сотен. В нем нет десятков, значит, на месте десятков поставьте нуль. В нем также нет единиц, поэтому и на месте единиц запишите нуль.
Это семьсот. При разложении 700 на разрядные слагаемые получается это же число.
Отлично, вы справились со сложной темой. А впереди вас ждет новое приключение.
Элли и ее друзьям предстоит переправиться через реку и спасти Страшилу, который повис на шесте посередине реки. Выполните практические задания, чтобы выручить друга.
Ответ: 260, 206, 620, 602
Ответ: четыре.
Умницы, и с этим заданием вы справились.
Сравнение трехзначных чисел
Ребята, мы дружно приближаемся к заветной цели. Осталось пройти последние испытания.
В жизни мы часто сравниваем явления природы, температуру за окном, высоту гор, глубину озер, рост людей, время, потраченное на упражнения. Предметы вокруг нас и величины имеют параметры, которые позволяют узнавать, что красивее, тяжелее, длиннее, мягче, выше. Животных сравниваем по повадкам, скорости передвижения, месту проживания.
Давайте познакомимся с математическими приемами сравнения однозначных, трехзначных, многозначных чисел.
Задания на сравнение можно выполнить разными способами:
Трехзначные числа всегда больше двузначных и однозначных просто потому, что в них больше разрядов. Однозначное число всегда меньше трехзначного; трехзначное больше двузначного.
Возьмем пару 512 и 612. Сравнение двух трехзначных чисел начинается с разряда сотен. В одном числе пять сотен, а в другом – шесть сотен. Значит второе больше чем первое.
Возьмем следующую пару 362 и 365. Опять начинаем сравнение слева направо. В разрядах сотен и десятков одинаковое количество. Значит, смотрим разряд единиц. 2 699
А вот триста сорок девять предшествует числу триста пятьдесят. Значит оно меньше.
Толкование трёхзначных чисел
В отношение трёхзначных чисел необходимо понять следующее: ни одна цифра внутри трёхзначного числа не может считаться главной или второстепенной с точки зрения её смысла. Всё цифры трёхзначного числа являются одинаково важными и определяющими.
Первая цифра определяющая, поскольку представляет собой энергетическую и смысловую причину, источник. Первая цифра – это «мама» и «папа» в одном лице для следующих двух цифр. Вторая и третья цифры трёхзначного числа, невзирая на их самостоятельные значения, отчасти будут отражать смысловые нюансы первой цифры, как дети отчасти обнаруживают некоторые свойства родителей. Кое-что «дети» усилят, кое-что ослабят, что-то изменят, что-то подтвердят – так родится смысл трёхзначного числа в целом.
Смысл трёхзначных чисел на примере числа 368
В числе 368 первопричиной является любовь, цифра 3. То есть энергия любви станет источником проявления числа 368 в нашей жизни. Любые трёхзначные числа, начинающиеся с с цифры 3, означают, что всё начиналось, или начинается, или начнётся с любви… Это может быть любовь к профессии, к женщине или мужчине, к Родине, к деньгам, к славе, к оружию — речь может идти о разных сторонах любви: и тёмных, и светлых. В языке чисел цифра 3 отражает только самую суть — Любовь.
Смысл чисел вообще всегда отражает лишь самую Суть. Её мы уже стараемся выразить более или менее подходящими словами, адаптировать к конкретному человеку, с учётом его характера, воспитания, генов, духовной зрелости и т.д.
Вторая цифра трёхзначного числа тоже определяющая, потому что она — связующее звено, сердцевина, метафизический и чисто логический мостик между смыслами первой и последней цифр. Вторая цифра указывает на тип связи между причиной и следствием, началом и концом, иллюзией рождения и иллюзией смерти… Почему иллюзией? Потому что для чисел нет рождения и смерти. Весь мир для них, включая нас с вами, – разные виды Энергии, и ничего больше.
Животное Я при всей своей ограниченности и глупости, как ни парадоксально, является необходимым звеном для обретения мудрости (мудрость — цифра 8 в числе 368). Ведь мудрость опирается на опыт. А для активного накопления опыта мы нуждаемся в беспрестанной мотивации, которую цифра 6 и обеспечивает в той или иной мере.
Слабая шестёрка (слабый земной огонь) недостаточно греет, недостаточно стимулирует, недостаточно вдохновляет. Не огонь, а огонёк. Он даёт слишком маленький опыт, чтобы можно было положить в копилку Мудрости что-то существенное. Именно поэтому равнодушные, инертные, безынициативные личности не становятся мудрее с годами. Исключение составляют тяжело больные люди. В силу своей печальной ограниченности они постигают мудрость не через активную жизненную позицию, а через Терпение, натренированное вынужденным бездействием. В подобном случае речь бы шла о числе 308, а не 368. Ноль означает созревание, терпение.
За результат проявления трёхзначного числа в обществе или конкретной человеческой судьбе отвечает третья цифра. То есть, значение последней цифры трёхзначного числа объясняет нам конечную цель. Конечная цель влияния на вас числа 368 – сделать вас мудрее (цифра 8) посредством любви (цифра 3) и опыта переживания разных страстей (цифра 6).
На какие трёхзначные числа следует обращать внимание
Уместно напомнить, что стоит обращать пристальное внимание лишь на те трёхзначные числа, которые настойчиво сопровождают вас в похожих ситуациях, или являются в качестве немедленного ответа на очередной вызов жизни. Натренированное сознание мгновенно «клюет» на такие числа. Остальным в помощь интуиция, внимание и здравый смысл.
Не волнуйтесь! Даже когда ваше сознание делает лишь первые, неуверенные шажки навстречу числам, их сознание (а числа безусловно обладают сознанием, хотя и отличным от нашего) помогает нам заполнить недостающие фрагменты энергетической мозаики.
Забавно, что получение нами ответов в виде чисел вовсе не обязательно означает, что мы сформулировали для себя некий конкретный вопрос о решении назревшей проблемы. Числа словно сами знают, что вам нужно. На самом деле не «знают», а только заполняют энергетические пустоты на уровне тонких духовных энергий. Числа просто указывают нам, на что обратить особое внимание. То есть, они показывают, чего нам не хватает или чего нет вовсе. Но иногда они приходят и в виде утешения, поддержки — типа «всё верно, ты на правильном пути». Я часто невольно задумываюсь о том, сколь многого люди лишают себя, не понимая языка чисел!
Порой для решения возникшей проблемы нам остаётся лишь расшифровать одно единственное число, часто попадающееся нам на глаза и примерить его смысл к себе, к своим желаниям, возможностям и обстоятельствам жизни.
Третья цифра трёхзначного числа – направление удара
Возвращаясь к толкованию трёхзначных чисел, хочу добавить: последнюю цифру в них для лучшего понимания можно ещё назвать «направлением удара».
Представьте, что в вашем распоряжении имеется хорошо вооружённое войско. Ваши воины закалены, опытны в сражениях и прекрасно обучены. Но если вы как полководец принимаете сумбурные, неэффективные решения и не в состоянии правильно определиться с направлением удара, то ваше войско не проявит свой подлинный потенциал. И возможно даже, вы проиграете сражение гораздо более слабому противнику!
В числе 368 последняя цифра подсказывает, что генеральное «направление удара» для ваших воинов (т.е. для ваших мыслей, чувств и поступков) – соблюдение главных принципов мудрости. Все они заключены в числе 8. Один из них наиболее актуален для повседневной жизни: «Не поступай с другими так, как не хочешь, чтобы поступали с тобой». Всё просто.
Как вы уже поняли, толкование трёхзначных чисел невозможно без глубокого понимания главных чисел духовной нумерологии от нуля до десяти. Их смысл подробно описан мной в книге «Духовная нумерология. Язык чисел», которую вы легко можете приобрести в любом книжном магазине или заказать онлайн на дом. Информации, что содержится в моей книге, вы не найдёте больше нигде – просто потому, что её больше нигде нет.
Трёхзначные числа — их гениальная точность и лаконичность
В заключение хочу добавить: каждое трёхзначное число представляет собой огромный пласт бесценной, эзотерической информации, сжатой всего в три последовательно выстроенные цифры. Меня всегда поражала удивительная лаконичность и меткость языка чисел!
Представьте, будто я рассказываю вам о чём-то три часа без перерыва. А мог бы лишь произнести: «542» или «393», или «925» — и все бы сразу поняли, о чём идет речь. Понимание одного числа способно заменить многочасовую речь! Например, если я сказал вам: «Автомобиль», вы сразу поняли, о чём я. Мне вовсе не нужно перечислять многочисленные рычаги и механизмы названного транспортного средства.
Так вот, любые числа – не только трёхзначные – уместно сравнить именно с этими сокращёнными словами и фразами, которые высокоразвитые души (те, что ныне уже не воплощаются) бегло накидали на холст Бытия, чтобы успеть за огромным количеством информации, беспрерывно льющейся из уст Творца.
Обратите внимание!
В магазины уже поступила моя книга под названием «Духовная нумерология. Язык чисел». На сегодняшний день это самое полное и востребованное из всех существующих эзотерических пособий о смысле чисел. Подробнее об этом, а также для заказа книги пройдите по следующей ссылке: «Духовная нумерология книга«
С теплом, автор книги и этого сайта Иосиф Лазарев
Натуральные числа являются привычными человеку и интуитивно понятными, ведь они окружают нас с самого детства. В статье ниже мы дадим базовое представление о смысле натуральных чисел, опишем основные навыки их записи и чтения. Вся теоретическая часть будет сопровождаться примерами.
Общее представление о натуральных числах
На определенном этапе развития человечества возникла задача подсчета неких предметов и обозначение их количества, что, в свою очередь, потребовало нахождения инструмента для решения этой задачи. Таким инструментом и стали натуральные числа. Понятно и основное предназначение натуральных чисел – давать представление о количестве предметов или порядковом номере конкретного предмета, если речь идет о множестве.
Логично, что для использования человеком натуральных чисел, необходимо иметь способ их воспринимать и воспроизводить. Так, натуральное число можно озвучить или изобразить, что является естественными способами передачи информации.
Рассмотрим базовые навыки озвучивания (чтения) и изображения (записи) натуральных чисел.
Десятичная запись натурального числа
Теперь возьмем как правило, что при изображении (записи) любого натурального числа используются только указанные цифры без участия любых других символов. Пусть цифры при записи натурального числа имеют одинаковую высоту, записываются одна за другой в строчку и слева всегда находится цифра, отличная от нуля.
Верная запись натурального числа, произведенная с учетом всех описанных требований, называется десятичной записью натурального числа.
Количественный смысл натуральных чисел
Как уже было сказано, натуральные числа изначально несут в себе, в том числе, количественный смысл. Натуральные числа, как инструмент нумерации, рассмотрены в теме о сравнении натуральных чисел.
Далее, по аналогии: Ψ Ψ Ψ – 3 предмета («три»), Ψ Ψ Ψ Ψ – 4 («четыре»), Ψ Ψ Ψ Ψ Ψ – 5 («пять»), Ψ Ψ Ψ Ψ Ψ Ψ – 6 («шесть»), Ψ Ψ Ψ Ψ Ψ Ψ Ψ – 7 («семь»), Ψ Ψ Ψ Ψ Ψ Ψ Ψ Ψ – 8 («восемь»), Ψ Ψ Ψ Ψ Ψ Ψ Ψ Ψ Ψ – 9 («девять»).
С указанной позиции функция натурального числа заключается в указании количества предметов.
Однозначные натуральные числа
Однозначное натуральное число – натуральное число, при записи которого используется один знак – одна цифра.
Двузначные и трехзначные натуральные числа
Двузначные натуральные числа – натуральные числа, при записи которых используются два знака – две цифры. При этом используемые цифры могут быть как одинаковые, так и различные.
Рассмотрим, какой смысл заключен в двузначных числах. Опираться будем на уже известный нам количественный смысл однозначных натуральных чисел.
Введем такое понятие как «десяток».
Представим множество предметов, которое состоит из девяти и еще одного. В таком случае можно говорить об 1 десятке («один десяток») предметов. Если представить один десяток и еще один, то речь пойдёт о 2 десятках («два десятка»). Прибавив к двум десяткам еще один, получим три десятка. И так далее: продолжая добавлять по одному десятку, мы будем получать четыре десятка, пять десятков, шесть десятков, семь десятков, восемь десятков и, наконец, девять десятков.
Трехзначные натуральные числа – натуральные числа, при записи которых используются три знака – три цифры. Цифры могут быть различными или повторяющимися в любом сочетании.
Чтобы понять количественный смысл трехзначных натуральных чисел, введем понятие «сотня».
Одна сотня ( 1 сотня) – это множество, состоящее из десяти десятков. Сотня и еще одна сотня составят 2 сотни. Прибавим еще одну сотню и получим 3 сотни. Добавляя постепенно по одной сотне, получим: четыре сотни, пять сотен, шесть сотен, семь сотен, восемь сотен, девять сотен.
Так, трехзначное натуральное число 402 обозначает: 2 единицы, 0 десятков (отсутствуют десятки, не объединенные в сотни) и 4 сотни.
По аналогии дается определение четырёхзначных, пятизначных и так далее натуральных чисел.
Многозначные натуральные числа
От всего вышесказанного теперь возможно перейти к определению многозначных натуральных чисел.
Многозначные натуральные числа – натуральные числа, при записи которых используются два и более знаков. Многозначные натуральные числа – это двухзначные, трехзначные и так далее числа.
Одна тысяча – множество, включающее в себя десять сотен; один миллион состоит из тысячи тысяч; один миллиард – тысяча миллионов; один триллион – тысяча миллиардов. Еще более крупные множества также имеют названия, но использование их редко.
Аналогично принципу выше, мы можем рассмотреть любое многозначное натуральное число, как набор однозначных натуральных чисел, каждое из которых, находясь на определенном месте, свидетельствует о наличии и количестве единиц, десятков, сотен, тысяч, десятков тысяч, сотен тысяч, миллионов, десятков миллионов, сотен миллионов, миллиардов и так далее (справа налево соответственно).
Например, многозначное число 4 912 305 содержит в себе: 5 единиц, 0 десятков, три сотни, 2 тысячи, 1 десяток тысяч, 9 сотен тысяч и 4 миллиона.
Резюмируя, мы рассмотрели навык группировки единиц в различные множества (десятки, сотни и т.д.) и увидели, что цифры в записи многозначного натурального числа являются обозначением количества единиц в каждом из таких множеств.
Чтение натуральных чисел, классы
В теории выше мы обозначили названия натуральных чисел. В таблице 1 укажем, как верно использовать названия однозначных натуральных чисел в речи и при буквенной записи:
Один
Два
Три
Четыре
Пять
Шесть
Семь
Восемь
Девять
Одна
Две
Три
Четыре
Пять
Шесть
Семь
Восемь
Девять
Одно
Два
Три
Четыре
Пять
Шесть
Семь
Восемь
Девять
| Число | Именительнный падеж | Родительный падеж | Дательный падеж | Винительный падеж | Творительный падеж | Предложный падеж |
| 1 2 3 4 5 6 7 8 9 | Один Два Три Четыре Пять Шесть Семь Восемь Девять | Одного Двух Трех Четырех Пяти Шести Семи Восьми Девяти | Одному Двум Трем Четырем Пяти Шести Семи Восьми Девяти | Один Два Три Четыре Пять Шесть Семь Восемь Девять | Одним Двумя Тремя Четырьмя Пятью Шестью Семью Восьмью Девятью | Об одном О двух О трех О четырех О пять О шести О семи О восьми О девяти |
Для грамотного прочтения и написания двузначных чисел, необходимо выучить данные таблицы 2 :
Мужской, женский и средний род
11
12
13
14
15
16
17
18
19
20
30
40
50
60
70
80
90
Одиннадцать
Двенадцать
Тринадцать
Четырнадцать
Пятнадцать
Шестнадцать
Семнадцать
Восемнадцать
Девятнадцать
Двадцать
Тридцать
Сорок
Пятьдесят
Шестьдесят
Семьдесят
Восемьдесят
Девяносто
| Число | Именительнный падеж | Родительный падеж | Дательный падеж | Винительный падеж | Творительный падеж | Предложный падеж |
| 10 11 12 13 14 15 16 17 18 19 20 30 40 50 60 70 80 90 | Десять Одиннадцать Двенадцать Тринадцать Четырнадцать Пятнадцать Шестнадцать Семнадцать Восемнадцать Девятнадцать Двадцать Тридцать Сорок Пятьдесят Шестьдесят Семьдесят Восемьдесят Девяносто | Десяти Одиннадцати Двенадцати Тринадцати Четырнадцати Пятнадцати Шестнадцати Семнадцати Восемнадцати Девятнадцати Двадцати Тридцати Сорока Пятидесяти Шестидесяти Семидесяти Восьмидесяти Девяноста | Десять Одиннадцать Двенадцать Тринадцать Четырнадцать Пятнадцать Шестнадцать Семнадцать Восемнадцать Девятнадцать Двадцать Тридцать Сорок Пятьдесят Шестьдесят Семьдесят Восемьдесят Девяносто | Десятью Одиннадцатью Двенадцатью Тринадцатью Четырнадцатью Пятнадцатью Шестнадцатью Семнадцатью Восемнадцатью Девятнадцатью Двадцатью Тридцатью Сорока Пятидесятью Шестидесятью Семидесятью Восьмидесятью Девяностью | О десяти Об одиннадцати О двенадцати О тринадцати О четырнадцати О пятнадцати О шестнадцати О семнадцати О восемнадцати О девятнадцати О двадцати О тридцати О сорока О пятидесяти О шестидесяти О семидесяти О восьмидесяти О девяноста |
Для того, чтобы читать трёхзначные числа, изучим данные таблицы 3 :
Двести
Триста
Четыреста
Пятьсот
Шестьсот
Семьсот
Восемьсот
Девятьсот
| Число | Именительный падеж | Родительный падеж | Дательный падеж | Винительный падеж | Творительный падеж | Предложный падеж |
| 100 200 300 400 500 600 700 800 900 | Сто Двести Триста Четыреста Пятьсот Шестьсот Семьсот Восемьсот Девятьсот | Ста Двухсот Трехсот Четырехсот Пятисот Шестисот Семисот Восьмисот Девятисот | Ста Двумстам Тремстам Четыремстам Пятистам Шестистам Семистам Восьмистам Девятистам | Сто Двести Триста Четыреста Пятьсот Шестьсот Семьсот Восемьсот Девятьсот | Ста Двумстами Тремстами Четыремстами Пятистами Шестистами Семистами Восьмистами Девятистами | О ста О двухстах О трехстах О четырехстах О пятистах О шестистах О семистах О восьмистах О девятистах |
Чтобы легко прочитать указанные натуральные числа, занесем их в таблицу:
| Класс триллионов | Класс миллиардов | Класс миллионов | Класс тысяч | Класс единиц |
| 134 | 678 | |||
| 31 | 013 | 736 | ||
| 23 | 476 | 009 | 434 | |
| 2 | 533 | 467 | 001 | 222 |
Разберем подробно чтение числа 2 533 467 001 222 :
— добавив название класса, получим: «два триллиона»;
— читаем следующее число, добавив название соответствующего класса: «пятьсот тридцать три миллиарда»;
— продолжаем по аналогии, зачитывая следующий класс правее: «четыреста шестьдесят семь миллионов»;
— читаем последний класс единиц, не добавляя его название – «двести двадцать два».
Таким образом, число 2 533 467 001 222 будет звучать так: два триллиона пятьсот тридцать три миллиарда четыреста шестьдесят семь миллионов одна тысяча двести двадцать два. Используя указанный принцип, прочтем и прочие заданные числа:
— 31 013 736 – тридцать один миллион тринадцать тысяч семьсот тридцать шесть;
— 134 678 – сто тридцать четыре тысячи шестьсот семьдесят восемь;
— 23 476 009 434 – двадцать три миллиарда четыреста семьдесят шесть миллионов девять тысяч четыреста тридцать четыре.
Таким образом, основой правильного прочтения многозначных чисел является навык разбивать многозначное число на классы, знание соответствующих названий и понимание принципа прочтения двух- и трехзначных чисел.
Разряды натурального числа, значение разряда
Как уже становится понятно из всего вышесказанного, от позиции, на которой стоит цифра в записи числа, зависит ее значение. Т.е., например, цифра 3 в составе натурального числа 314 обозначает количество сотен, а именно – 3 сотни. Цифра 2 – количество десятков ( 1 десяток), а цифра 4 – количество единиц ( 4 единицы). При этом мы будем говорить, что цифра 4 находится в разряде единиц и является значением разряда единиц в заданном числе. Цифра 1 стоит в разряде десятков и служит значением разряда десятков. Цифра 3 располагается в разряде сотен и является значением разряда сотен.
Разряд – это позиция цифры в записи натурального числа, а также и значение этой цифры, которое определяется ее позицией в заданном числе.
Разряды имеют свои названия, мы уже использовали их выше. Справа налево следуют разряды: единиц, десятков, сотен, тысяч, десятков тысяч и т.д.
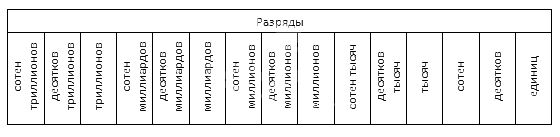
Для удобства запоминания можно использовать следующую таблицу (укажем 15 разрядов):
Уточним такую деталь: количество разрядов в заданном многозначном числе такое же, как количество знаков в составе записи числа. К примеру, данная таблица содержит названия всех разрядов для числа, в котором 15 знаков. Последующие разряды также имеют названия, но используются крайне редко и очень неудобны для восприятия на слух.
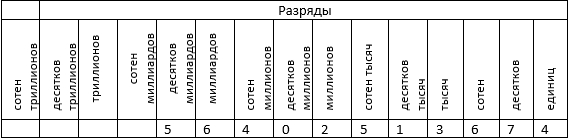
При помощи такой таблицы возможно наработать навык определения разряда, записывая заданное натуральное число в таблицу так, чтобы крайняя правая цифра была записана в разряде единиц и далее – в каждый разряд по цифре. К примеру, запишем многозначное натуральное число 56 402 513 674 так:
Введем также еще понятия низшего и высшего разрядов многозначного числа.
Низший (младший) разряд любого многозначного натурального числа – разряд единиц.
Высший (старший) разряд любого многозначного натурального числа – разряд, соответствующий крайней левой цифре в записи заданного числа.
Так, например, в числе 41 781 : низший разряд – разряд единиц; высший разряд – разряд десятков тысяч.
Логически следует, что возможно говорить о старшинстве разрядов относительно друг друга. Каждый последующий разряд при движении слева направо ниже (младше) предыдущего. И наоборот: при движении справа налево каждый следующий разряд выше (старше) предыдущего. К примеру, разряд тысяч старше разряда сотен, но младше разряда миллионов.
Уточним, что при решении некоторых практических примеров используется не само натуральное число, а сумма разрядных слагаемых заданного числа.
Кратко о десятичной системе счисления
Система счисления – метод записи чисел при помощи знаков.
Позиционные системы счисления – такие, в которых значение цифры в составе числа зависит от ее позиции в записи числа.
Помимо нее, существуют и прочие системы счисления. Например, информатика использует двоичную систему. Когда же мы ведем счет времени, то задействуем шестидесятеричную систему счисления.